函数算术均值极限的黎曼积分形式及其在R0命题逻辑中的应用
2016-11-17吴洪博王伦磊
吴洪博,王伦磊
(陕西师范大学数学与信息科学学院,陕西西安 710119)
函数算术均值极限的黎曼积分形式及其在R0命题逻辑中的应用
吴洪博,王伦磊
(陕西师范大学数学与信息科学学院,陕西西安 710119)
提出并证明了在有界闭域上非负且黎曼可积的多元函数的算数平均值极限的黎曼积分形式,还证明了n值R0命题逻辑中当n趋于无穷大时公式的广义真度极限的存在定理;并根据在有界闭域上非负且黎曼可积的多元函数的算数平均值极限的黎曼积分形式和n值R0命题逻辑中当n趋于无穷大时公式的广义真度极限的存在定理,在连续值R0命题逻辑中建立了相对于局部有限理论的公式的广义真度理论,为在R0命题逻辑中建立基于局部有限理论的近似推理,广义积分语义理论等奠定了基础.
计量逻辑;黎曼积分;R0命题逻辑;局部有限理论;广义真度
电子学报URL:http://www.ejournal.org.cn DOI:10.3969/j.issn.0372-2112.2016.08.020
1 引言
上世纪二十年代,Lukasiewicz关于三值命题逻辑的论文on three-valued logic的发表标志着多值命题逻辑研究工作的开始[1].1998年Hájek 于文献[2]中的研究工作是对基于连续t-模建立的命题逻辑的系统总结.进入二十一世纪,我国学者徐扬教授建立了格值命题逻辑,已故学者王国俊教授建立了R0命题逻辑,王三民教授建立了NML命题逻辑,国外学者F Estava,L Gødo 建立了MTL命题逻辑等等[3~7],这些命题逻辑的建立进一步丰富了多值命题逻辑的研究内容.
语义理论是多值逻辑不可分割的组成部分,语义理论的研究与发展始终伴随着多值命题逻辑的研究与发展.二十一世纪初期王国俊教授提出的模糊推理的三I算法理论,广义重言式理论,计量逻辑理论是关于语义理论研究的重要组成部分.文献[7~23]是关于这些理论研究所取得的重要成果.文献[24~26]将计量逻辑理论中的真度方法应用于多值模态逻辑和基于有限迁移系统的线性时态逻辑的计量化方法的研究之中,并取得了一些重要成果.计量逻辑中的基本理论是公式的真度理论[7,8],文献[9]在n值R0命题逻辑中建立了公式相对于局部有限理论的广义真度理论.本文的主要内容是在连续值R0命题逻辑中引入与n值R0命题逻辑中广义真度相和谐的公式相对于局部有限理论的广义真度理论.首先,根据R0命题逻辑中公式的广义真度理论研究的需要,给出了在测度不等于零的有界闭域上多元非负可积函数的算数平均值极限的黎曼积分形式;其次,证明了n值R0命题逻辑中当n→∞时广义真度极限的存在定理,特别地,当公式所诱导的逻辑函数在由局部有限理论所决定的积分区域的测度不等于零时,给出了广义真度极限的黎曼积分形式;最后,根据n值R0命题逻辑中当n→∞时广义真度极限的存在定理,在连续值R0命题逻辑中建立了公式相对于局部有限理论的广义真度理论.本文的结果将n值R0命题逻辑和连续值R0命题逻辑通过相对于局部有限理论的公式的广义真度和谐地结合起来,将有助于计量逻辑理论,近似推理理论,积分语义理论的进一步推广和发展.
2 预备知识
定义1[7]R0命题逻辑中的公式集F(S)是由可数无穷集S={p1,p2…}和逻辑连接词┐,→,∧生成的(1,2,2)型自由代数(F(S),(┐,→,∧)).称S中的元为命题变元.此外,在F(S)中将┐(┐A∧┐B)记作A∨B.
R0命题逻辑中的推理规则是MP规则.
其中的公理集请参见文献[7].

┐x1=1-x1,x1∧x2=min{x1,x2},
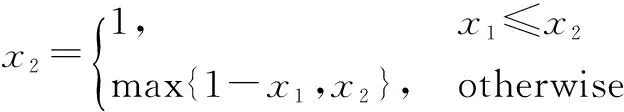
分别称(Wn,(┐,∧,⟹)),(W,(┐,∧,⟹))为n值R0代数与R0单位区间,将它们分别记作Wn,W.
定义3[7]映射v:F(S)→Wn(或W)称为F(S)的赋值,如果v是(┐,∧,⟹)型代数同态.以Wn为赋值域的命题逻辑称为n值R0命题逻辑,以W为赋值域的命题逻辑称为连续值R0命题逻辑.用Ω记以Wn或W为赋值域的全体赋值之集.

3 多元非负函数算术均值的极限定理
本节中有关黎曼积分,算数平均值等概念和性质请参考文献[28].
定理1 非负函数算术均值的极限定理
设a 以Δn表示点(ξ1,…,ξm)所在的小方体与D相交的点的集合.则 证明 我们仅以二元函数为例进行证明 由题设知f(x1,x2)在有界闭域D上黎曼可积,我们应用黎曼积分的定义对∫Df(x1,x2)dx1dx2进行计算. 首先,[a,b]2中分点满足:当i=0,1,…,n时, D的分割是上述小方体δ(ξ1,ξ2)与D的交集构成的集族,D的分割成员分为三类,记: 令S=∫Ddx1dx2,则由题设知S>0并且由文献[28]知∃M>0使得∀(x1,x2)∈D,0≤f(x1,x2)≤M. 在D的分割中,分块具有以下性质: 因此,∀ε>0,∃N∈Z+使得当n≥N时, =ε 因此,结合黎曼积分的定义[28]得 ∫Df(x1,x2)dx1dx2 文献[7,8]中真度理论是从有限值命题逻辑和连续值命题逻辑两个方面建立的.文献[9]在n值R0命题逻辑中通过计算公式属于Γ-重言式之集的隶属度的方法建立了公式相对于局部有限理论的广义真度理论,但并未在连续值R0命题逻辑中建立与之相对应的广义真度理论,或相对应的广义积分语义理论.本节我们将证明在n值R0命题逻辑中广义真度极限的存在性以及给出特定条件下广义真度极限的黎曼积分形式. 首先,设Γ∪{A}⊆F(S),我们给出如下约定:SΓ={p∈S|∃B∈Γ,p出现B中},SA=S{A}.如果SΓ是有限集合,则称Γ是F(S)的局部有限理论. 定义5[9]在n值R0命题逻辑中,设Γ是F(S)的局部有限理论,A∈F(S),i∈{0,1,…,n-1}, Σ(Γ)={v∈Ω∀B∈Γ,v(B)=1}≠∅, 当Σ(Γ)=∅时,约定τn(Γ,A)=1. 称τn(Γ,A)是公式A的Γ-真度. 其中vSΓ∪SA∶SΓ∪SA→Wn是赋值v:F(S)→Wn在SΓ∪SA上的限制. 注1 ∀i,j∈{0,1,…,n-1},当i≠j时, 定理2 广义真度极限的存在定理 证明 在定义5中,Γ-真度可以表示为: 定理3 广义真度的均值形式 在n值R0命题逻辑中,设Γ是F(S)的局部有限理论,A∈F(S),SΓ∪SA={p1,p2,…,pm}, 证明 (1)∀i∈{0,1,…,n-1}, (2)∀i∈{0,1,…,n-1},定义hi:N(Γ,A,i)→Δn(Γ,A,i)如下:hi(v|{p1,…,pm})=(v(p1),…,v(pm)).参照文献[9]可以证明:hi是双射. 定理4 广义真度极限的积分形式 证明 由文献[27]可知公式A诱导的函数 根据n值R0命题逻辑中广义真度极限的存在定理和广义真度极限的黎曼积分形式,本节中我们将在连续值R0命题逻辑中给出公式相对于局部有限理论的广义真度的合理形式,使得通过广义真度的形式将有限值R0命题逻辑和连续值R0命题逻辑和谐的结合在一起. 证明 这是定理4和定义6的直接结果. 例1 在连续值R0命题逻辑中,设 Γ1={(p1→p2)→p2},Γ2={p1→p2,p2→p1}.A=p1∧p2.请计算τ[0,1](Γ1,A),τ[0,1](Γ2,A). 解答 (1)由公式(p1→p2)→p2诱导的函数形式是(x1⟹x2)⟹x2.根据定义2,定义4可知 因此, Δ[0,1](Γ1,A)={(x1,x2)∈[0,1]2|(x1⟹x2)⟹x2=1} =4×∫Δ[0,1](Γ1,A)(x1∧x2)dx1dx2 因此根据定义6得: 本文将在有界闭域上非负且黎曼可积的多元函数算术平均值极限的黎曼积分形式和n值R0命题逻辑中公式相对于局部有限理论的广义真度的极限存在定理相结合,在连续值R0命题逻辑中建立了公式相对于局部有限理论的广义真度理论,不但进一步完善了R0命题逻辑中公式相对于局部有限的广义真度理论,而且使得两种R0命题逻辑通过广义真度理论的形式紧密的联系在一起,同时为在R0命题逻辑中建立基于局部有限理论的广义真度理论的近似推理理论,计量逻辑理论,积分语义理论等奠定了基础. 致谢 作者对评审人和编委给出的诚挚的修改建议表示衷心感谢. [1]J Lukasiewicz.O Trówartosciowej (On three-valued logic)[J].Ruch Filozoficzny,1920,5(2):170-171. [2]P Hájek.Metamathematics of Fuzzy Logic[M].Dordrecht:Kluwer Academics Publisher,1998. [3]Y Xu,D Ruan,K Y Qin,J Liu.Lattice-Valued Logic[M].Berlin Heidelberg:Springer-Verlag,2003. [4]F Esteva,L Gødo.Monoidal t-norm-based logic:towards a logic for left-continuous t-norms[J].Fuzzy Sets and Systems,2001,124(3):271-288. [5]S M Wang,B S Wang,F Ren.NML,a schematic extension of F.Esteva and L.Gødo's logic MTL[J].Fuzzy Sets and Systems,2005,149(2):285-295. [6]张小红.模糊逻辑及其代数分析[M].北京:科学出版社,2008(第一版). [7]王国俊.非经典数理逻辑与近似推理[M].北京:科学出版社,2008(第二版). [8]G J Wang,H J Zhou.Quantitative logic.Information Science[J].2009,179(3):226-247. [9]H B Wu.The generalized truth degrees of quantitative logic in the logic system L*n[J].Computers and Mathematics with Applications,2010,59(8):2587-2596. [10]H W Liu,G J Wang.Triple I method based on point-wise sustaining degrees[J].Computers and Mathematics with Applications,2008,55(11):2680-2688. [11]H W Liu,G J Wang.Unified forms of fully implication restriction methods for fuzzy reasoning[J].Information Sciences,2007,177(3):956-966. [12]H B Wu.The theory of generalized tautologies in the revised Kleene system[J].Science in China (Series E),2001,44(3):233-238. [13]汪德刚,谷云东,李洪兴.模糊模态命题逻辑及其广义重言式[J].电子学报,2007,35(2):261-264. Wang Degang,Gu Yundong,LI Hongxing.Fuzzy modal logic and its tautologies[J].Acta Electronica Sinica,2007,35(2):261-264.(in Chinese) [14]王国俊,宋建设.命题逻辑中的程度化方法[J].电子学报,2006,34(2):252-257. WANG Guo-jun,SONG Jian-she.Graded method in propositional logic[J].Acta Electronica Sinica,2006,34(2):252-257.(in Chinese) [15]李骏,王国俊.逻辑系统Ln*中的命题真度理论[J].中国科学:E 辑,2006,36(6):631-643. LI Jun,WANG Guo-jun.Theory of truth degrees of propositions in logic system Ln*[J].Science in China:Information science,2006,36(6):631-643.(in Chinese) [16]吴洪博,周建仁,张琼.(3n+1)值逻辑系统R0L中公式的真度性质[J].电子学报,2011,39(10):2230-2234,2229. Wu Hongbo,Zhou Jianren,Zhang Qiong.The properties of truth degrees of formulas in (3n+1)-valued logic system R0L[J].Acta Electronica Sinica,2011,39(10):2230-2234,2229.(in Chinese) [17]李骏,姚锦涛.命题逻辑系统SMTL中公式的积分真度理论[J].电子学报,2013,41(5):878-883. LI Jun,YAO Jin-tao.Theory of integral truth degrees of formula in SMTL propositional logic[J].Acta Electronica Sinice,2013,41(5):878-883.(in Chinese) [18]吴洪博,周建仁.计量逻辑中真度的均值表示及其应用[J].电子学报,2012,40(9):1822-1828. Wu Hongbo,Zhou Jianren.The form of mean representation of truth degree with application in quantitative logic[J].Acta Electronica Sinica,2012,40(9):1822-1828.(in Chinese) [19]张东晓,李立峰.二值命题逻辑公式的语构程度化方法[J].电子学报,2008,36(2):320-325. Zhang Dongxiao,Li Lifeng.Syntactic graded method of 2-va;ued propositional logic formulas[J].Acta Electronica Sinica,2008,36(2):320-325.(in Chinese) [20]吴洪博.Lukasiewicz命题逻辑中公式的Γ-真度和极限定理[J].中国科学:信息科学,2014,44(12):1542-1559. WU Hong-bo.Limit theorem and Γ-truth degrees in Lukasiewicz propositional logic[J].Science in China:Information Science,2014,44(12):1542-1559.(in Chinese) [21]周红军,折延宏.Lukasiewicz命题逻辑中命题的Choquet积分真度理论[J].电子学报,2013,23(3):557-563. Zhou Hongjun,She Yanhong.Theory of Choquet integral truth degrees of propositions in Lukasiewicz propositional logic[J].Acta Electronica Sinica,2013,23(3):557-563.(in Chinese) [22]胡明娣,王国俊.经典逻辑度量空间中的模2次范整线性空间结构[J].电子学报,2011,39(4):899-905. Hu Ming-di,Wang Guo jun.Z(2)-normal linear structure on classical logic metric space[J].Acta Electronica Sinica,2011,39(4):899-905.(in Chinese) [23]胡明娣,王国俊.对称逻辑公式在经典逻辑度量空间中的分布[J].电子学报,2011,39(2):419-423. Hu Ming-di,Wang Guo-jun.Distribution of the symmetrical logic formulas in the classical logic metric space[J].Acta Electronica Sinica,2011,39(2):419-423.(in Chinese) [24]王国俊,段巧林.模态逻辑中的(n)真度理论与和谐定理[J].中国科学(F辑),2009,39(2):234-245. WANG Guo-jun,DUAN Qiao-lin.Harmonious theorem and (n) truth degrees in model logic[J].Science in China:Information Science,2009,39(2):234-245.(in Chinese) [25]时慧娴,王国俊.多值模态逻辑的计量化方法[J].软件学报,2012,23(12):3074-3087. SHI Hui-xian,WANG Guo-jun.Quantitative method of multi-valued model logic[J].Journal of Software,2012,23(12):3074-3087.(in Chinese) [26]时慧娴,王国俊.基于有限迁移系统的线性时态逻辑的计量化方法[J].模糊系统与数学,2012,26(5):30-35. SHI Hui-xian,WANG Guo-jun.A quantitative approach for linear temporal logic based on finite transition system[J].Fuzzy system and Mathematics,2012,26(5):30-35.(in Chinese) [27]周建仁,吴洪博.R0-蕴涵算子所导出的逻辑函数的特征[J].数学学报(中文版),2014,57(2):235-248. Zhou Jianren,Wu Hong-bo,Characterizations of logic functions derived by R0-operator[J].Acta Mathematics Sinica,2014,57(2):235-248.(in Chinese) [28]华东师范大学数学系编.数学分析[M].北京:高等教育出版社,2001(第三版). [29]徐新亚.实变函数论[M].上海:同济大学出版社,2010. 吴洪博 男,1959年出生,陕西咸阳人,四川大学理学博士,陕西师范大学教授,研究方向为格上拓扑与模糊逻辑. E-mail:wuhb @ snnu.edu.cn 王伦磊 女,1991出生,陕西安康人,陕西师范大学硕士研究生,研究方向为非经典数理逻辑. Riemann Integral form of Limit of Arithmetic Mean Value of a Function and Its Application in R0Propositional Logic System WU Hong-bo,WANG Lun-lei (CollegeofMathematicsandInformationScience,ShaanxiNormalUniversity,Xi’an,Shaanxi710119,China) The Riemann integral form of limit of arithmetic mean value of a non-negative and Riemann integrable function with multiple variables in a bounded closed domain is proposed and proved.Secondly,the existence theorem of limit of generalized truth degree of a formula inn-valued R0propositional logic is obtained.Thirdly,the theory of generalized truth degrees is proposed in continuously valued R0propositional logic by combining of the Riemann integral form of limit of arithmetic mean value of a non-negative and Riemann integrable function with multiple variables in a bounded closed domain and the existence theorem of limit of generalized truth degree of a formula inn-valued R0propositional logic,which provides the foundation for establishing theories of approximate reasoning and generalized integral semantics based on locally finite theory in R0propositional logic. quantitative logic;Riemann integral;R0propositional logic;locally finite theory;generalized truth degree 2015-01-28; 2015-07-27;责任编辑:马兰英 国家自然科学基金(No.61572016,No.11531009);中央高校基本科研业务专项资金(No.GK201501001) O141.1 A 0372-2112 (2016)08-1909-06

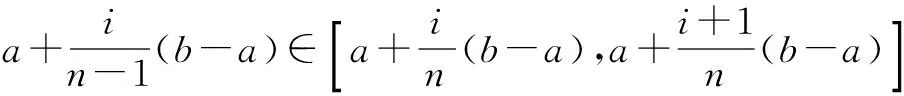

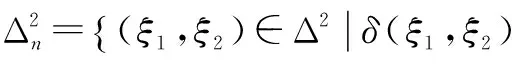



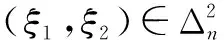


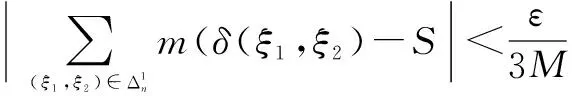
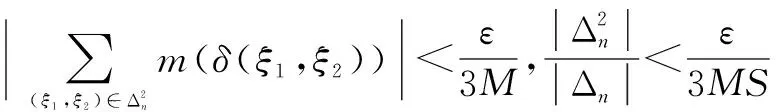


4 n值R0命题逻辑中广义真度极限




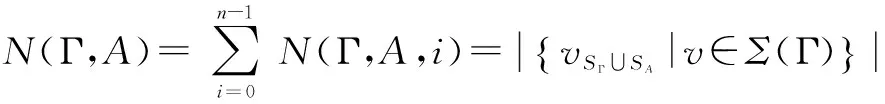

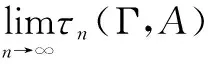

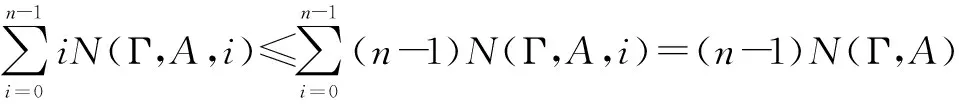
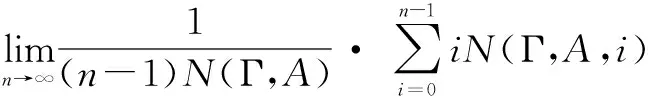

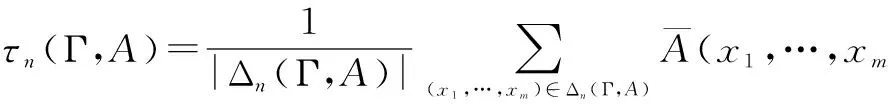
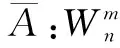

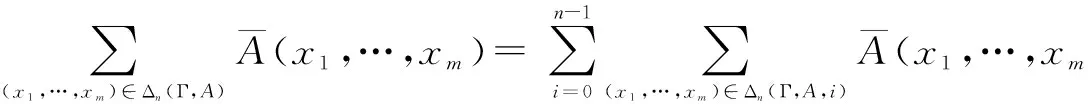


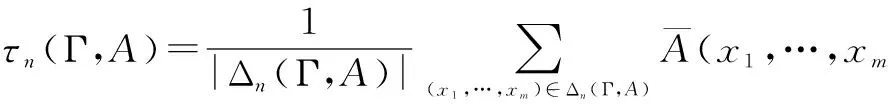

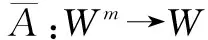

5 连续值R0命题逻辑中的广义真度


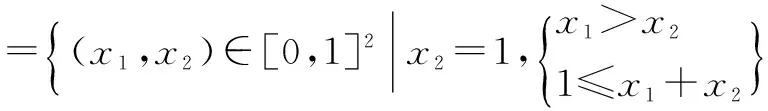

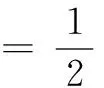
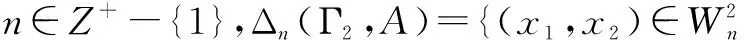


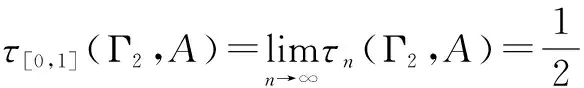
6 后记

