基于形状及空间关系的场景相似性检索

田泽宇,门朝光,汤亚楠

(哈尔滨工程大学计算机科学与技术学院,黑龙江哈尔滨 150001)



基于形状及空间关系的场景相似性检索

田泽宇,门朝光,汤亚楠

(哈尔滨工程大学计算机科学与技术学院,黑龙江哈尔滨 150001)

为解决空间数据检索效率低、准确性差的问题,本文提出由空间对象形状描述模型、空间关系描述模型、场景相似性自适应计算模型构成的场景相似性检索方法.空间对象形状描述模型精准检索满足样例对象形状约束的数据库对象,提高空间对象形状的识别精度.空间关系描述模型检索满足样例场景关系约束的数据库场景,提高空间关系的描述精度.场景相似性自适应计算模型对满足形状及关系约束的完全匹配、局部匹配场景进行打分、排序,增加检索结果相似性打分的合理性.模拟场景、真实场景的实验表明本场景相似性检索方法具有良好的检索性能.

空间数据检索;形状描述;空间关系描述;场景相似性

电子学报URL:http://www.ejournal.org.cn DOI:10.3969/j.issn.0372-2112.2016.08.018

1 引言

随着空间数据获取技术的迅速发展,空间数据规模呈爆炸增长趋势,在海量空间数据中快速检索出需要的信息是目前空间数据管理的瓶颈.传统的空间数据检索方法主要有基于位置和关键字的检索、Spatial SQL查询语言和可视化空间数据检索,这些方法很难表达复杂的拓扑、方向关系,而且语法复杂、描述模糊,极易出错.为了解决这些问题,使用基于草图、基于样例等更直观、更符合人类认知的检索方式,进行更精准的场景相似性检索.Egenhofer首次提出了基于草图的空间数据检索,并设计了拓扑关系、方向关系和拓扑关系的概念邻域图等模型[1,2].以拓扑关系为基础,文献[3]研究了拓扑关系相似性度量方法,并使用独立成分分析和模糊支持向量机进行空间数据检索.以方向关系为基础,文献[4]研究了确定区域间方向关系的度量方法,文献[5]给出了不确定区域间方向关系的相似性度量方法.以拓扑和方向关系为基础,文献[6]给出了草图的一阶邻近关系和相应的前项检查检索方案,文献[7]通过草图空间关系的定性表达和校准,将草图信息整合到GIS系统中.以上相似性度量方法均没有考虑空间对象形状对相似性检索的影响,而且在检索结果的相似性打分、排序上没有给出详尽的方案.文献[8,9]设计了组件相似性、匹配完整性等场景相似性打分机制,但没有设定自适应的相似性权重参数,也没有考虑对象的形状.

为了提高场景相似性检索的精度,使用了空间对象形状相似性度量方法.现有空间对象形状相似性研究主要有多级弦长描述法[10]、弯曲度半径描述法[11]、正切空间描述法[12]等.但这些方法描述能力不强,不能兼顾形状的边界和区域信息.

针对现有场景相似性检索的缺陷,本文提出基于形状及空间关系的场景相似性检索方法.本检索方法通过空间对象形状描述模型精准检索满足样例对象形状相似性约束的数据库对象,通过空间关系描述模型定性、定量地检索满足样例场景关系约束的数据库场景,通过场景相似性自适应计算模型对检索到的数据库场景进行打分、排序,得到与样例场景相似的所有完全匹配、局部匹配场景,提高空间对象形状及关系的检索识别精度,增加场景检索结果相似性打分的合理性.

2 空间对象形状描述模型

本文提出的空间对象形状描述模型通过计算空间对象形状的主方向,利用与主方向平行的若干条直线分割空间对象,计算同一分割线上对象分割段之间的顺序特征描述量f,记录所有分割线上的顺序特征描述量{f1,f2……fn},形成空间对象的形状特征描述量F={f1,f2……fn}.

空间对象的形状主方向由空间对象的形状特征决定,是空间对象形状的最小惯性轴.主方向位于通过重心且倾角为θ的直线上,倾角θ公式为[13]:

(1)

其中,u11,u02,u20为空间对象区域的p+q阶中心矩.空间对象形状主方向如图1中带箭头的直线所示.

求出与主方向平行且与空间对象最外侧相交的两条边界线,如图1中的两条实线所示.利用与主方向平行的n条直线将两条边界线之间的部分平均分割为n+1等份,如图1中的9条虚线将实线之间的部分平均分割为10等份.

某一条分割线与空间对象相交于m段(m≥1),如图1中分割线L1与空间对象相交于ab、cd两段,分割线L2与空间对象相交于mn一段,分割线L3与对象相交于三段.同一条分割线上的对象分割段均为直线,不存在形状差异,但对象分割段之间有前后顺序.假定分割线为一维坐标轴,可任意规定该一维坐标轴的正方向,但所有分割线的正方向必须相同,如图1中规定主方向的箭头方向为正方向.图1中分割线L1的对象分割段cd领先于分割段ab,即段cd中任一点u均领先于段ab中任一点v,设函数φ(u-v)描述点u、v的顺序关系,公式为:

(2)

则段ab与段cd之间所有点的顺序关系描述即顺序特征描述量f可表示为:

(3)

其中,x、z分别为线段cd、ab的长度.y为点c与点b坐标值之差.当点c领先于点b时,y>0;当点c与点b重合时,y=0;当点b领先于点c时,y<0.

更一般的,假设一条分割线上的对象分割段为I1、I2,则公式(3)可表示为:

(4)

其中,x为段I2的长度,z为段I1的长度.y为段I2的起点坐标与段I1的终点坐标之差.u为段I2上的点,v为段I1上的点.

当一条分割线上的对象分割段多于两段时,如图1中分割线L3与空间对象相交于三段.假设该条分割线上的对象分割段为I1、I2……In,n为大于2的整数,则该条分割线上的顺序特征描述量f为:

(5)

当一条分割线上只有1个对象分割段时,如图1中分割线L2上的段mn.此时可以看做两个长度为x的段mn、m′n′完全重合,根据公式(4)可得:

(6)

即分割线上只有一个对象分割段I时,公式(6)为:

(7)

其中,x为分割段I的长度,u和v为段I上的点.

(8)

(9)

则两个对象vi、uj的形状相似度为:

Svertex=1-dvertex

(10)

本文的空间对象形状描述模型可以精确描述空间对象形状的整体特征和细节信息,兼顾了边界和区域信息,具有平移、旋转、翻转、尺度不变性,对形状的轻微形变具有鲁棒性,并且可以通过调节分割线数量对空间对象形状进行多级描述.

3 空间关系描述模型

本文利用维度扩展9交模型(DE-9IM)[14],提取样例场景和数据库场景中面空间对象间的拓扑关系,在数据库场景中检索与样例场景拓扑关系一致的场景.当样例场景中两个对象间的拓扑关系为相离或相交时,需要引入定量度量机制对相离、相交关系进行细化.

当场景中两个对象A、B的拓扑关系为相离时,通过空间对象形状相似性的计算可知空间对象的重心位置和主方向上所有对象分割段的长度之和.设相离空间对象A、B各自主方向上所有分割段的长度之和分别为Da、Db,两个相离空间对象的重心距离为Dc,相对于空间对象A的相离关系定量度量为DIS1,相对于空间对象B的相离关系定量度量为DIS2.DIS1、DIS2可表示为:

(11)

在进行场景相似性匹配时,设样例场景空间对象vi、vk之间相离关系的定量度量为DIS1(v)、DIS2(v),数据库场景空间对象uj、ul之间相离关系的定量度量为DIS1(u)、DIS2(u),样例场景相离关系和对应数据库场景相离关系的差异度为:

(12)

则样例场景和对应数据库场景的相离关系相似度Sedge可表示为:

(13)

当场景中两个对象A、B的拓扑关系为相交时,设对象A、B的面积分别为area(A)、area(B),相交部分A∩B的面积为area(A∩B),相对于空间对象A的相交关系定量度量为LAP1,相对于空间对象B的相交关系定量度量为LAP2.LAP1,LAP2公式为:

(14)

在进行场景相似性匹配时,设样例场景空间对象vi、vk之间相交关系的定量度量为LAP1(v)、LAP2(v),数据库场景空间对象uj、ul之间相交关系的定量度量为LAP1(u)、LAP2(u),样例场景相交关系和对应数据库场景相交关系的差异度为:

(15)

则样例场景和对应数据库场景的相交关系相似度Sedge可表示为:

(16)

DE-9IM不能描述对象间的方向关系,本文基于方向关系矩阵模型[4],计算目标对象在参考对象9个方向片内的部分占自身的比例,忽略对方向关系影响不大的部分.

4 空间场景相似性检索

在空间对象形状描述模型与空间关系描述模型的基础上,提取样例场景中每个对象的形状描述量、对象间的拓扑关系和方向关系,利用每个样例对象的形状描述量检索数据库场景中形状相似的对象,判断检索到的数据库对象是否满足样例对象间的拓扑关系和方向关系.根据形状相似度、拓扑中相离关系和相交关系的相似度以及检索到场景的完整性,对获得的数据库场景进行相似性打分和排序.设样例场景为S、数据库场景为D,样例场景S包含n个空间对象{v1,v2,……vn},数据库场景D包含m个空间对象{u1,u2,……um}.样例场景S如图2(a)所示,数据库场景D如图2(b)所示.

4.1 建立关联图

计算样例场景S中空间对象vi的形状描述量与数据库场景D中空间对象uj的形状描述量的相似度,当两个对象的形状相似度在阈值范围内时,生成关联图Ga的顶点aij,记录空间对象vi和空间对象uj的形状匹配相似度.

计算关联图Ga中任意两个顶点aij、akl之间是否有边相连,需要判断数据库场景空间对象uj、ul之间的拓扑关系和方向关系是否满足样例场景空间对象vi、vk之间的拓扑关系和方向关系.若满足,则关联图中两个顶点aij、akl之间建立边相连接,并记录空间关系的相似度为1.0;否则,不建立边.当拓扑关系为相离关系或相交关系时,需要计算样例场景和对应数据库场景的相离关系相似度或相交关系相似度.判断相离关系相似度、相交关系相似度是否在阈值范围内,若在范围内,则建立边并记录相离、相交关系相似度.图2的样例场景和数据库场景的关联图如图3所示.

4.2 提取关联图的极大团

提取关联图Ga中的所有极大团,检索出与样例场景完全匹配、局部匹配的所有数据库场景.其中,最大团对应场景的完全匹配,极大团对应场景的局部匹配.本文以极大团提取算法ELS[15]为基础,根据空间场景相似性检索的特点,对关联图Ga进行优化,降低关联图的复杂度,提高极大团提取的效率,提高场景相似性检索的效率.

在空间场景相似性检索中,数据库场景D的对象数目通常远大于样例场景S的对象数目,有可能导致样例场景S中的空间对象有很多形状相似的数据库对象,但这些形状相似的数据库对象都很难完全满足样例场景S中空间关系的约束,最终会导致关联图中出现大量的孤立点或度为1的顶点,这些顶点可以在执行算法ELS前去除,降低关联图的复杂度,提高极大团的提取效率.

在建立关联图Ga={V,E}过程中,将每个顶点v的度和邻接点集合Γ(v)记录在该顶点v中,并记录所有孤立点和度为1的顶点.关联图Ga极大团提取算法的实现步骤如下:

(1)将孤立点从关联图中去除,并将去除的孤立点作为极大团,记为样例场景的匹配,利用公式(17)至(21)计算其场景相似性.

(2)将度为1的顶点从关联图中去除,其邻接顶点Γ(v)的度均减1,并将该顶点和其邻接顶点作为极大团,记为样例场景的匹配,利用公式(17)至(21)计算其场景相似性.去除该顶点之后,继续判断该顶点的邻接顶点的度.如果度为0,则直接去除;如果度为1,则重复步骤2;如果大于1,则停止.

(3)利用算法ELS提取经步骤1、2优化后的关联图Ga1的极大团,将提取出的极大团记为样例场景的匹配,利用公式(17)至(21)计算其场景相似性.

设关联图Ga有w个顶点,经步骤1、2优化后的关联图Ga1为有N个顶点的d-退化图.关联图Ga极大团提取算法步骤1、2的线性时间复杂度为O(w-N),步骤3的时间复杂度为O(d*N*3d/3)[15].因关联图Ga中存在大量的孤立点和度为1的顶点,优化关联图Ga,可以进一步减少ELS算法的执行时间,提高场景相似性检索的效率.

图3中的关联图先通过步骤1将孤立点{C,6}去除,将该点记为样例场景的局部匹配,计算该点的相似性.通过步骤2将度为1的顶点{A,7}{B,8}去除,将顶点{A,7}{B,8}记为样例场景的局部匹配,计算该局部匹配的相似性.通过步骤3检索出优化关联图的最大团{A,1}{B,2}{C,3}和最大团{A,4}{B,2}{C,3},将两个最大团分别记为样例场景的完全匹配,计算完全匹配的相似性.

4.3 空间场景相似性自适应计算模型

利用对象组件相似性、关系组件相似性、场景匹配完整性等机制,设计新的场景相似性自适应权重参数,提出空间场景相似性计算模型,对得到的匹配场景进行打分、排序.

4.3.1 组件相似性

在极大团中,根据每个顶点记录的样例场景和数据库场景中匹配对象的形状相似性Svertex,计算整个匹配场景的空间对象组件相似性SObj,公式为:

(17)

其中,M表示极大团的顶点个数即匹配场景的对象个数;Svertexi表示极大团中第i个顶点记录的形状相似性;mi表示极大团的第i个匹配对象对中构成样例空间对象的点数,m表示样例场景中所有已匹配空间对象的点数.wOi表示极大团中第i个顶点的权重,为第i个已匹配样例对象的点数占样例场景中所有已匹配对象的点数的比.样例场景中构成对象的顶点数越多代表该对象形状越复杂,越容易在数据库场景中找到匹配的对象,其在场景中的权重wOi也越大.

在极大团中,根据每条边记录的样例场景和数据库场景中对应空间关系的相似性Sedge,计算整个匹配场景的空间关系组件相似性SRel,公式如下:

(18)

其中,M表示极大团的顶点个数;Sedgei表示极大团中第i条边记录的空间关系相似性;wRi表示极大团中第i个关系的权重.本文所有关联关系的权重均相同,取值为1.

4.3.2 场景完整性

依据人类对空间场景的主观认知,完全匹配场景的相似性分值比局部匹配场景的相似性分值高,因此局部匹配中未匹配的样例空间对象对该局部匹配的相似性分值有负面影响.本文用空间场景完整性Scomp反映场景匹配的程度,公式如下:

(19)

4.3.3 空间场景相似性计算

空间场景相似性的计算利用了对象组件相似性SObj、关系组件相似性SRel和空间场景完整性Scomp的计算结果,其计算公式为:

(20)

其中,wObj表示对象组件相似性所占的权重,wRel表示关系组件相似性所占的权重.

本文通过形状描述模型检索空间对象,当空间对象形状复杂时,形状的辨识度要高于空间关系的辨识度.空间对象最简单的形状为三角形,当空间对象的形状全为三角形时,权重wObj=wRel;当空间对象的形状不全为三角形时,权重wObj>wRel.通常情况下对象组件相似性的权重wObj高于关系组件相似性的权重wRel,权重公式如下:

(21)

其中,n表示样例场景中已匹配对象的数目,m表示样例场景中已匹配对象的顶点数目.

5 实验及结果分析

本实验分为两个部分,先使用通过真实建筑构建的形状数据集和北京大学矢量地图验证空间对象形状描述模型的有效性,再利用文献1中的模拟场景数据库和清华大学矢量地图验证整体检索方案的有效性.

5.1 空间对象形状描述模型实验

使用从OpenStreetMap中获取的北京大学约1400个建筑的地图作为实验数据,如图4所示.本实验仅使用空间对象形状描述模型,在地图中任选3个建筑作为样例对象,检索结果只显示相似度最高的3个建筑,检索结果如图5所示.从检索结果中可以看出,三组实验均准确地检索出了样例对象本身,其形状相似性均为1.0.本实验表明了空间对象形状描述模型可以精准识别空间对象的形状,对形状的轻微形变具有鲁棒性.

从真实地图中选取70个形状各异的建筑物,如图6中上方图所示;对每一个建筑物分别缩放0.49、0.7、1.37倍,得到3个建筑物,如图6中下方图第一行从左至右依次是原始建筑、缩放0.49倍建筑、缩放0.7倍建筑、缩放1.37倍建筑.对原始建筑和3个缩放建筑分别旋转45度、135度、225度得到12个建筑,如图6中下方图第二行、第三行、第四行的建筑分别为第一行建筑旋转45度、135度、225度.对原始建筑进行四种仿射变换,得到4个建筑,如图6中下方图第五行所示.对每个建筑共进行了19次变换,得到了19个建筑,加上原始建筑,构成了一类相似建筑的20种形变.70个原始建筑共形成了70类,每类20个相似建筑,共1400个建筑的形状数据集.

对形状数据集中的每个建筑均进行一次检索,共进行1400次检索实验.在每次实验检索出的前40个建筑中,计算检索建筑的相似建筑个数,相似建筑个数与该类相似建筑总数20的比值为该建筑的检索率,所有建筑检索率的平均值为平均检索率.文献10、11和本文空间对象形状描述法的平均检索率如表1所示.本文对象形状描述法的平均检索率高于其他2个形状描述法,具有更强的对象形状描述能力,具有平移、旋转、翻转和尺度不变性,对因仿射变换造成的形状形变具有一定的鲁棒性.

表1 三种空间对象形状描述法的平均检索率

5.2 空间场景相似性检索实验

文献[1]中的模拟场景数据库共有1000个场景,每个场景由6个面区域组成.从模拟场景数据库中选取30个不同类的场景作为样例进行检索实验,检索结果的例子如图7所示.两个例子中所有检索结果的对象形状、拓扑关系和方向关系均满足样例场景的要求,所有检索结果的场景完整性Scomp均为1,影响检索结果相似性分数的只为对象形状和相离关系的相似度.通过实验,30个不同场景检索的查准率和查全率均为100%,样例场景本身的相似性分数均最高为1.0.

绘制文献1模拟场景数据库中60个不同类场景的草图,进行检索实验.文献6与本相似性检索方案的查准率和查全率如表2所示.本检索方案的查准率、查全率均高于文献6方案,这是因为本检索方案加入了空间对象的形状约束,形状描述模型的精准识别提高了检索准确率.

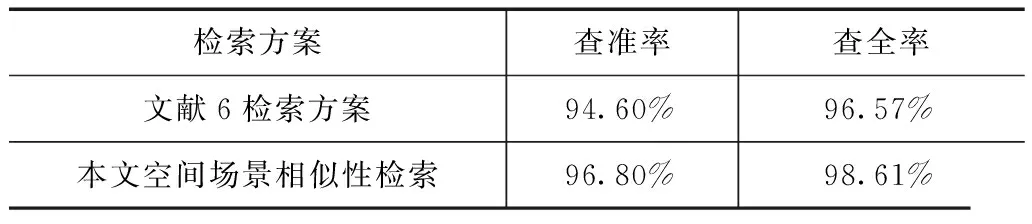
表2 查准率和查全率

以从OpenStreetMap中获取的清华大学约1100个建筑的地图为实验数据,通过程序提供的草图绘图功能,绘制要检索的样例场景,如图8所示,实验结果如图9所示.图8右侧绘制形状较为复杂的清华大学图书馆(最下方建筑)、新斋(最上方建筑)等四个建筑物为样例场景,由于图书馆、新斋这两个建筑形状过于复杂、特殊,形状描述模型可以准确找到对应的匹配对象,而中间两个形状简单的建筑却可以找到很多形状相似的匹配对象.通过相离关系的定量度量和方向关系的描述识别,形成了草图的完全匹配和中间两个建筑的部分匹配.

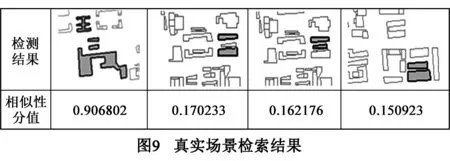
从实验结果看出,完全匹配的相似度很高为0.906802,中间两个建筑的部分匹配相似度很低.因为样例场景中图书馆、新斋两个建筑的形状复杂、辨识度高,这两个建筑的重要性远大于中间两个建筑,所以中间两个建筑部分匹配的场景完整性Scomp很低小于0.19,导致部分匹配的场景相似度低.

6 结论

本文提出了基于形状及空间关系的场景相似性检索方法,并给出了空间对象形状描述模型、空间关系描述模型、场景相似性自适应计算模型,提高了空间对象形状的识别精度、空间关系的描述精度和场景相似性检索的精度,增加了场景检索结果相似性打分的合理性,为复杂空间场景提供了更直观、精度更高的相似性检索方法.

[1]Egenhofer M J.Query processing in spatial-query-by-sketch[J].Journal of Visual Languages and Computing,1997,8(4):403-424.

[2]Egenhofer M J.Qualitative spatial relation reasoning for design[A].Studying Visual and Spatial Reasoning for Design Creativity [C].Netherlands:Springer Netherlands,2015.153-175.

[3]袁贞明,吴飞,等.基于草图内容的空间拓扑数据检索方法[J].浙江大学学报(工学版),2006,40 (10):1663-1669.

Yuan Zhen-ming,Wu Fei,et al.Spatial topological data retrieval based on sketch content[J].Journal of Zhejiang University (Engineering Science),2006,40 (10):1663-1669.(in Chinese)

[4]Goyal R K.Similarity assessment for cardinal directions between extended spatial objects[D].Maine:University of Maine,2000.36-49.

[5]孙伟,欧阳继红,等.不确定区域间方向关系的相似性度量方法[J].电子学报,2014,42(3):597-601.

Sun Wei,Ouyang Ji-hong,et al.Similarity assessment of approximate direction relations[J].Acta Electronica Sinica,2014,42(3):597-601.(in Chinese)

[6]申世群,刘大有,等.基于草图的空间数据检索研究[J].电子学报,2010,38(8):1819-1824.

Shen Shi-qun,Liu Da-you,et al.Research on spatial data retrieval based on sketch[J].Acta Electronica Sinica,2010,38(8):1819-1824.(in Chinese)

[7]Jan S,Schwering A,et al.Qualitative representations of extended spatial objects in sketch maps[A].Proceedings of International AGILE′2014 Conference[C].Spain:Springer International Publishing,2014.37-54.

[8]Nedas K A,Egenhofer M J.Spatial scene similarity queries[J].Transactions in GIS,2008,12(6):661-681.

[9]He B,Wang D,Chen C.A novel method for mineral prospectivity mapping integrating spatial-scene similarity and weights-of-evidence[J].Earth Science Informatics,2015,8(2):393-409.

[10]安晓亚,孙群,等.一种形状多级描述方法及在多尺度空间数据几何相似性度量中的应用[J].测绘学报,2011,40(4):495-508.An Xiao-ya,Sun Qun,et al.A Shape multilevel description method and application in measuring geometry similarity of multi-scale spatial data[J].Acta Geodaetica et Cartographica Sinica,2011,40(4):495-508.(in Chinese)

[11]付仲良,逯跃锋.利用弯曲度半径复函数构建综合面实体相似度模型[J].测绘学报,2013,42(1):145-151.Fu Zhong-liang,Lu Yue-feng.Establishment of the comprehensive model for similarity of polygon entity by using the bending radius complex function[J].Acta Geodaetica et Cartographica Sinica,2013,42(1):145-151.(in Chinese)

[12]Fan H,Zipf A,et al.Quality assessment for building footprints data on openstreetmap[J].International Journal of Geographical Information Science,2014,28(4):700-719.

[13]Zunic J,Rosin P L,et al.On the orientability of shapes[J].IEEE Transactions On Image Processing,2006,15(11):3478-3487.

[14]Strobl C.Dimensionally extended nine-intersection model (DE-9IM)[A].Encyclopedia of GIS[C].New York:springer-Verlag,2008.240-245.

[15]Eppstein D,Strash D.Listing all maximal cliques in large sparse real-world graphs[A].Proceedings of the 10th International Conference on Experimental Algorithms[C].Berlin:Springer Verlag,2011.364-375.

田泽宇 男,1987年生,黑龙江佳木斯人,哈尔滨工程大学博士生,主要研究方向为空间数据检索、图像处理.

E-mail:tianzeyu @hrbeu.edu.cn

门朝光 男,1963年生,黑龙江哈尔滨人,哈尔滨工程大学教授,主要研究方向为信息安全、空间数据检索、图像处理.

E-mail:menchaoguang@hrbeu.edu.cn

Spatial-Scene Similarity Retrieval Based on Shape and Spatial Relation

TIAN Ze-yu,MEN Chao-guang,TANG Ya-nan

(CollegeofComputerScienceandTechnology,HarbinEngineeringUniversity,Harbin,Heilongjiang150001,China)

To solve the problem of low efficiency and poor accuracy on spatial data retrieval,this paper proposes a scene similarity retrieval method based on spatial object shape description model,spatial relationship description model and adaptive scene similarity computing model.Spatial object shape description model can accurately retrieve database objects satisfied with the sample object shape constraints,and improve the space object shape recognition accuracy.Spatial relationship description model can retrieve database scenes satisfied with relationship constraints of the sample scene,and improve the spatial relationship description precision.Adaptive scene similarity computing model can mark and sequence complete or incomplete matching scenes satisfied with shape and relationship constraints,improve the rationality of similarity scores on retrieval results.Experiments of simulative and real scenes show the scene similarity retrieval has a good retrieval performance.

spatial data retrieval;shape description;spatial relation description;spatial-scene similarity

2015-07-30;

2015-10-11；责任编辑：蓝红杰

TP391.3

A

0372-2112 (2016)08-1892-07