组合式摆动实验仪的研制

毛爱华，蔡 禄

(内蒙古科技大学，内蒙古 包头 014010)



组合式摆动实验仪的研制

毛爱华，蔡 禄

(内蒙古科技大学，内蒙古 包头 014010)

介绍一种组合式摆动实验仪，它可以将三线摆、两线摆、扭摆和单摆这四种实验仪器巧妙组合在一起，成为一种新的实验仪，具有一台实验仪测量多种摆动的功能,可以实现多种物理量的测量以及对不同摆动规律的研究，有效节约购置仪器成本。

三线摆；两线摆；扭摆；单摆；组合式摆动实验仪

三线摆法测定物体转动惯量、两线摆法测定物体转动惯量、扭摆法测定物体转动惯量和单摆运动规律研究均是大一普物力学经典实验。在摆角较小时均为简谐振动[1]，振动原理相同，实验器材基本相同，每种仪器功能单一；现将四个实验仪器巧妙组合在一起，可以实现一台实验仪可以做多个实验内容和多种测量研究，一台仪器多种功能，有效节约购置仪器成本，该实验仪可以作为学生的一项设计性实验内容，用于测量物体转动惯量和研究物体的各种摆动规律。

1 实验原理

1.1 三线摆实验仪

三线摆实验是通过测量其扭转运动的周期来测量刚体的转动惯量的.下圆盘可绕中心轴扭转,其扭转周期和下圆盘上所放置刚体的质量分布有关[2]。

转动惯量是描述刚体转动中惯性大小的物理量，其大小表现了刚体转动状态改变的难易程度，它与刚体的质量分布及转轴位置有关。对于形状复杂、质量分布不均匀的刚体，通常利用三线摆法进行测量[3-4]。

(1)转动惯量测量

三线摆空载时悬盘转动惯量为

(1)式中m0为悬盘质量,T0为悬盘绕中心轴的转动周期,R0为下盘悬线端点到转轴的距离,r0为上盘悬线端点到转轴的距离,H为上下两盘之间的垂直距离。

(2)加载圆盘前后转动周期变化规律[5]

将质量为m1的待测圆盘放在悬盘上,其半径为R1,质心位于中心轴上,圆盘与悬盘组成一个系统,转动周期为T1,根据

(2)

研究加载圆盘前后转动周期变化规律以及加载半径不同的圆盘系统周期T1的变化规律。

(3)加载圆环前后转动周期的对比[5]

将质量为m2待测圆环放在悬盘上,其有效半径为R2,质心位于中心轴上,圆环与悬盘组成一个系统,转动周期为T2,令圆环为细环,则有

(3)

(4)放置圆环后转动周期T2随半径R2的变化[5]

(4)

(5)放置圆环后转动周期T2随质量m2的变化[5]

(5)

(6)验证平行轴定理

本装置的三线摆悬盘上刻有若干同心圆，将三个同样大小的质量为m钢球放置在均匀分布于半径为R3的圆周上的三个孔上[6]，如图(4)测出三个球对中心轴的转动惯量Jx。

平行轴定理：如果一刚体对通过质心的某一转轴的转动惯量为Je。则这刚体对平行于该轴、且相距为d的另一轴的转动惯量为J＇x=Je+md2。

如果测得的Jx与J＇x计算的结果在误差范围内相符，则验证平行轴定理。

1.2 两线摆实验仪

将金属棒的两端与上圆盘的5、6小孔连接可构成两线摆，如图(1)。式m0中为金属棒质量,T0为棒绕中心轴的转动周期,L为金属棒端点到转轴的距离，H为上盘到金属棒之间的垂直距,r0为上盘悬线端点到转轴的距离,转动惯量为

(6)

在金属棒上对称打若干个小坑，小坑内可以放置完全相同的钢质小球。可以测定小球绕轴转动惯量，研究平行轴定理。

1.3 扭摆实验仪

在金属丝下端悬挂一可放置环状刚体的圆盘状刚体或三爪盘,即构成扭摆实验仪 如图(5)。当圆盘的转动惯量为已知时,可以间接测得金属丝的切变模量；反之,当金属丝的切变模量为已知时,可以测定圆盘的转动惯量.还可以验证刚体转动惯量的重要性质之一:平行轴定理[7]。

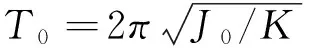
1.4 单摆实验仪

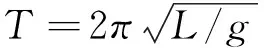
2 仪器结构

实验仪包括支架1、上转盘2、悬线7、金属丝8、扭摆圆盘(圆环)9、下圆盘10、球体11、均质金属杆12、底座13、摆球14，配置块15，小孔3、小孔4、小孔5，小孔6、卡栓16，固定螺丝17，仪器装置如图1。

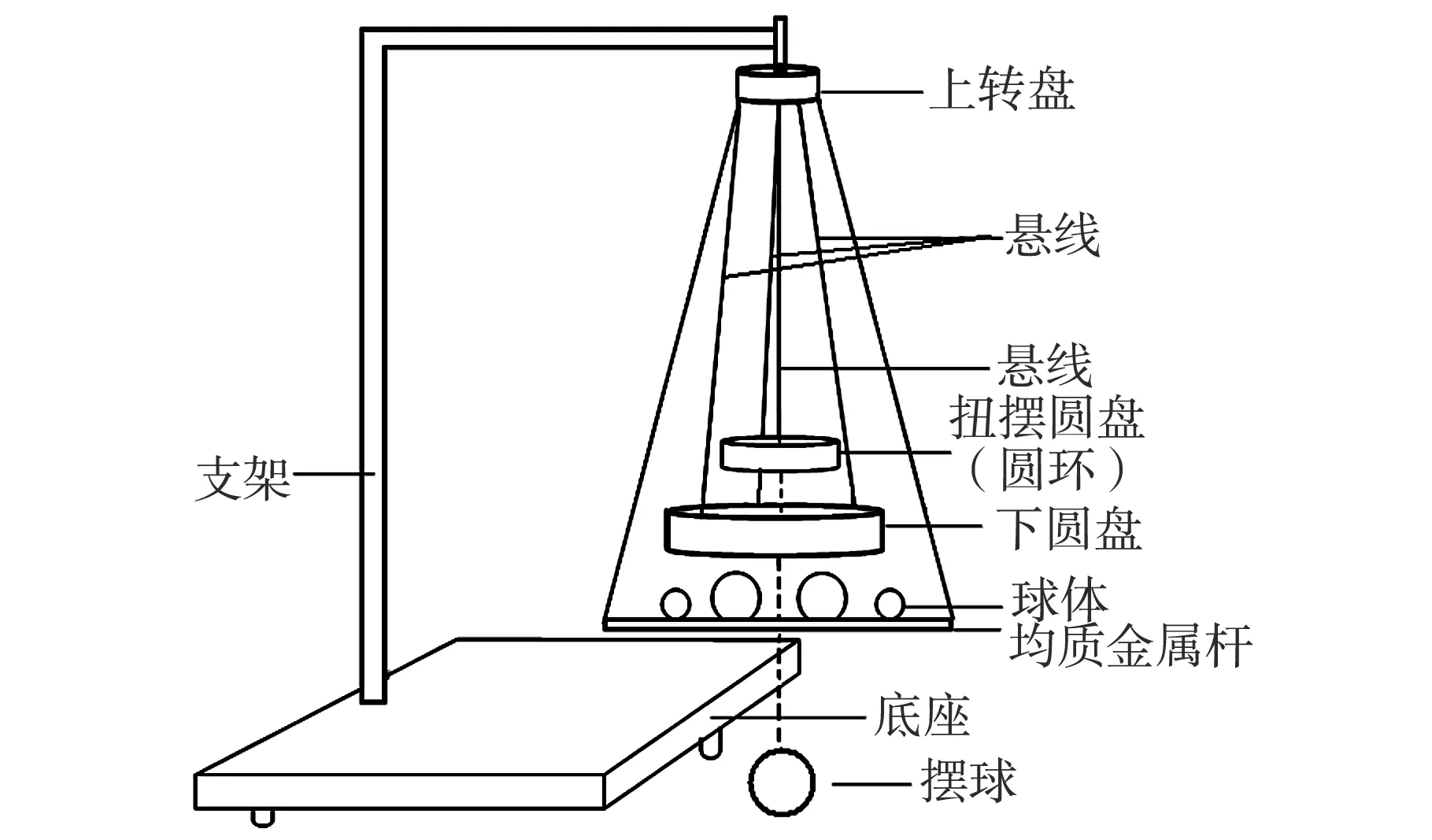
图1 组合式摆动实验仪

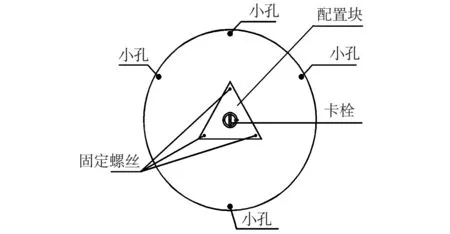
图2 上转盘平面结构示意图

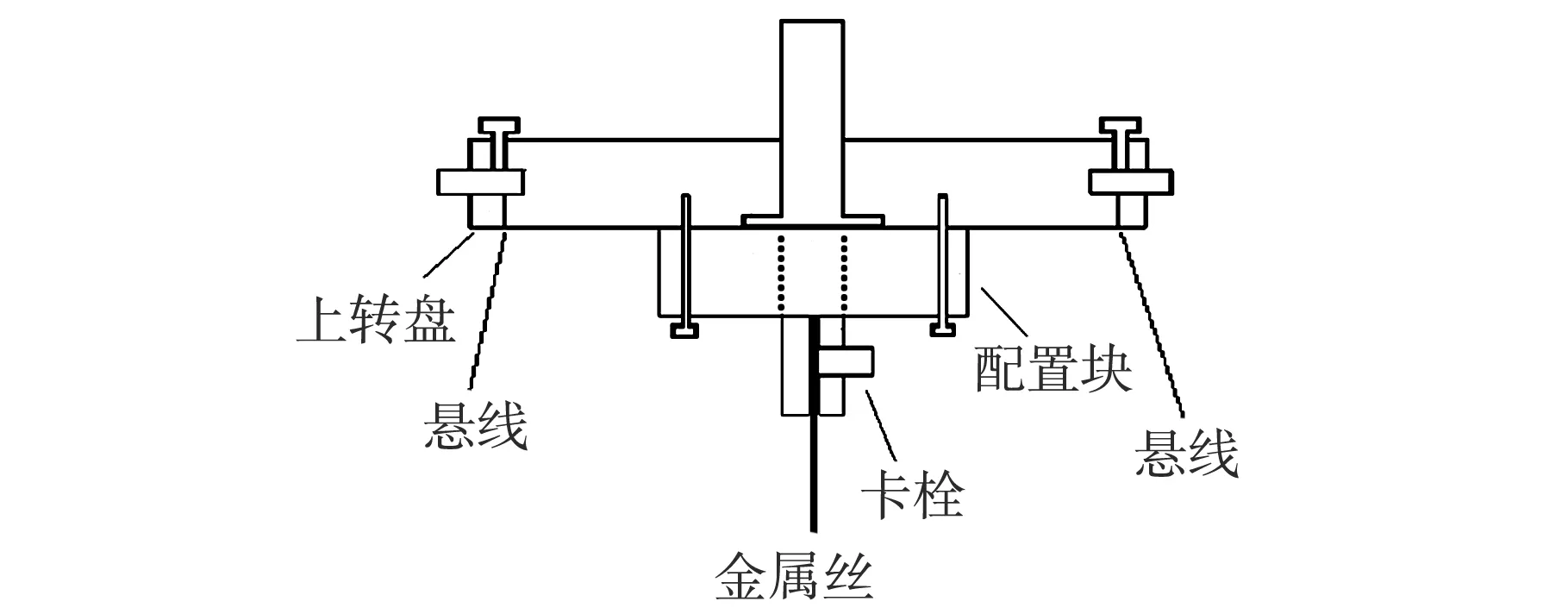
图3 上转盘剖面结构示意图

3 实验仪研制、创新部件

本实验仪在现有三线摆实验仪基础上进行创新，对其上转盘重新设计、制作，研制内容如下：

(1)上转盘间隔120°设有小孔3、4、5，分别由小孔穿悬线联接下悬盘的对称位置，即构成三线摆；下悬盘刻有若干同心圆刻线，将三个同样大小的钢球放置在均匀分布于半径为R1的圆周上的三个孔上，如图4所示。

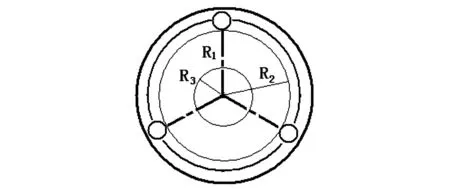
图4 下悬盘俯视示意图

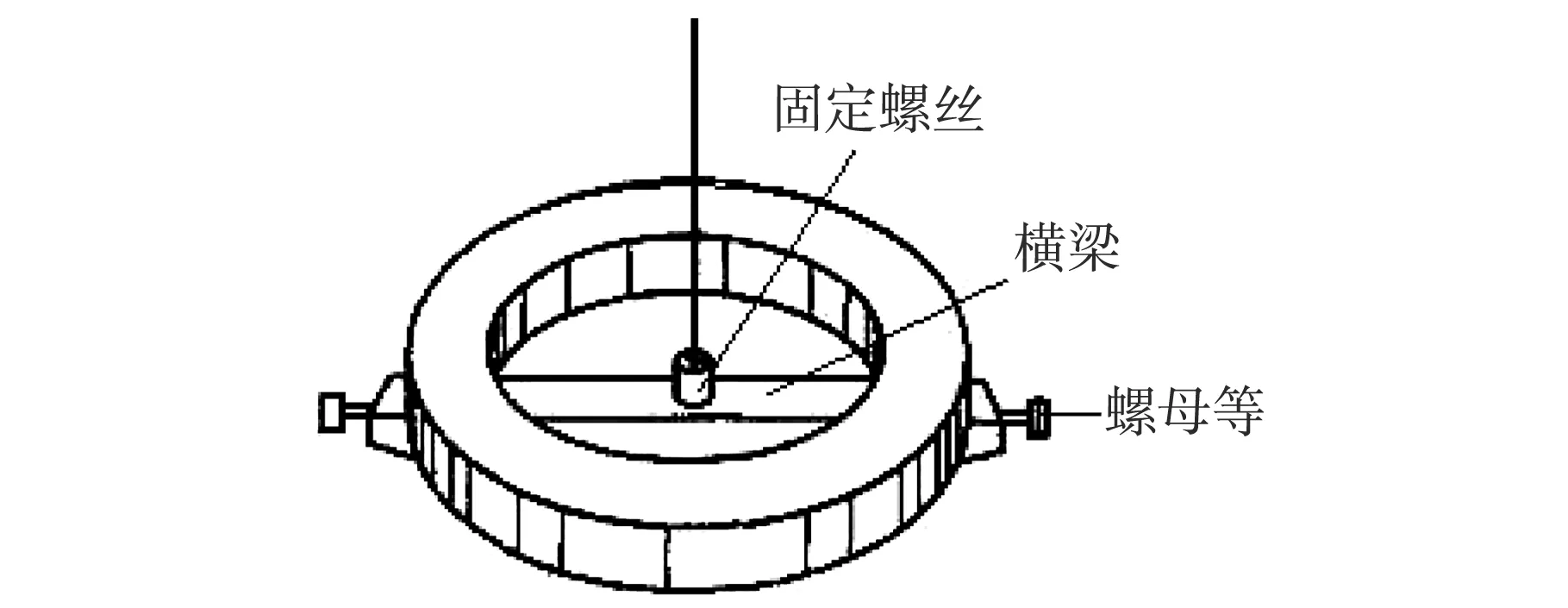
图5 扭摆示意图

(2)上转盘原设有小孔3、4、5，由5通过轴心的延长线上的对称位置处再打一个孔6，如图2所示，小孔5与孔6上分别系有悬线，悬线下端与金属杆12连接，构成两线摆。

(3)上转盘下表面中心处安装有配置块15，配置块15上带有卡栓16；金属丝8上端与卡栓16固定，如图所示3，下端悬挂卡线圆盘9，构成扭摆。

扭摆吊钩主要夹子丝扣17、横梁18、螺母等19组成，如图5所示；夹子丝扣可夹紧金属丝，横梁用来水平放置形状规则的刚体(圆环、圆柱体)，横梁两端的是一对平衡螺母，以调节横梁的平衡。

(4)上转盘下表面中心处安装有配置块，其上带有卡栓16，卡栓16中夹一悬线，如图3所示；悬线下端挂一金属小球14，构成单摆，如图1所示。

(5)本实验装置采用中用光控数字毫秒计测量周期的方法：可测定组合装置中的各种摆动周期。读数能精确到10-3s，可直接测量时间间隔，且具有时间间隔的积累功能和时间的记忆、查阅功能；积累的时间间隔数(时间段)由0到100可调，按上、下箭头键可查阅每个时间段的大小，以便挑选扭摆摆动最稳定的时间段作为测量数据，以提高测量的准确度。

4 结 论

组合式摆动实验仪：金属支架、数字毫秒计、水平仪、米尺，待测物体(圆盘、圆环、小球)、等器材实现共享。将三线摆、两线摆、扭摆和单摆这四种实验仪器巧妙组合在一起，亦可拆装。测量时分立使用，实现一台仪器多项功能，学生可以根据三线摆、两线摆、扭摆、单摆的实验原理、测量方法进行不同物理量的测量及不同摆动规律的研究，该实验装置亦可以作为大学生科技创新项目，此实验仪器已获国家实用新型发明专利[11-12]。

[1] 朱瑜，潘永丰，左安友．不同摆角对三线摆测量转动惯量的影响[J].湖北民族学院学报:自然科学版，2014(2)：156-158，161.

[2] 王玉清，杨能勋,黄保瑞.三线摆加上刚体后振动周期变化的研究[J].大学物理，2009,28(4)：14-17.

[3] 丁慎训,张孔时.物理实验教程[M].北京：清华大学出版社，1992:32-35.

[4] 成正维.牛原[M].北京：北京交通大学出版社，2010:54-55.

[5] 毛爱华，刘官员，董大明.放置不同物体三线摆转动惯量周期变化规律研[J].大学物理，2009,28(4)：18-19.

[6] 贾小兵，杨茂田，殷洁等.大学物理实验教程[M].北京：人民邮电出版社，2003:59-63.

[7] 杨述武,马葭生,等.普通物理实验(一.力学及热学部分)[M].北京:高等教育出版社,2001:97-102.

[8] 张平.切变模量和转动惯量实验的改进[J].大学物理，2006，25(5)：28-31.

[9] 陈莹梅，刘平安.基于垂直轴定理的新型扭摆实验仪实验研究[J].实验室研究与探索,2006,25(11):1363-1365.

[10] 李纪强,周斌,丁益民.单摆混沌现象的研究[J].湖北大学学报,2013,35(4)：513-517.

[11] 毛爱华,李国锋,吕海龙.组合式摆动实验仪[J].中国，实用新型专利[P].ZL 2012 2 0550019.X,2012(6):19.

[12] 董大明,毛爱华,李丽荣.三线摆转动惯量实验仪[J].中国，实用新型专利[P] ZL 2011 2 0209051.7,2011(12):28.

[13] 娄航宁，王威，孙维民.三线摆测量转动惯量方法的改进及不确定度分析[J].大学物理实验，2015(6)：102-105.

[14] 蔡慧卿，周婧也，竺江峰，等.不同线长高度测量圆盘转动惯量产生误差的研究[J].大学物理实验，2016，29(2)：11-18.

Making Combined Wiggle Apparatus

MAO Ai-hua,CAI Lu

(Inner Mongolia University of Science and Technology,Inner Mongolia Baotou 014010)

Four kinds of the physical experiment apparatus including three-wire pendulum,two-wire pendulum,torsional pendulum and simple pendulum were combined together to form a new wiggle apparatus which can carry out measure for several kinds of swing easily.

three-wire pendulum；two-wire pendulum；torsional pendulum；simple pendulum；combined wiggle apparatus

2016-05-29

1007-2934(2016)05-0106-04

O 4-33

A DOI：10.14139/j.cnki.cn22-1228.2016.005.027