融合多特征的天基典型目标光学识别方法
2016-11-17智喜洋侯晴宇
智喜洋,侯晴宇,张 伟,孙 晅
(哈尔滨工业大学 航天学院,哈尔滨150001)
融合多特征的天基典型目标光学识别方法
智喜洋,侯晴宇,张 伟,孙 晅
(哈尔滨工业大学 航天学院,哈尔滨150001)
为满足天基近距离目标高精度探测和识别的需求,提出一种多特征融合的卫星局部识别方法.首先分析卫星局部物理特征,构建了融合形态学多特征参量的局部构件分形聚类参数集,并建立基于聚类特征加权组合的构件聚类模型.利用该模型即可实现通过计算待识别目标隶属于各构件类的匹配性概率来识别目标;在此基础上,针对空间目标光学成像的图像降质、局部遮挡等问题,提出了目标识别算法,并以其在实际应用中的识别概率为依据,结合粒子群算法迭代优化加权系数,提高了识别算法效率与鲁棒性;最后利用4类典型卫星及伽利略卫星缩比模型对识别算法进行了数字仿真和半物理实验验证.实验结果表明,在低对比度、SNR仅为5,且构件存在较严重变形与互遮挡的情况下,算法仍能有效识别卫星构件,识别概率优于0.95.
天基目标识别;卫星局部;多特征参量;聚类模型;识别算法
随着航天技术的迅速发展,以卫星为主体的空间军事设施已成为信息化、现代化战争不可或缺的战略资源,因此围绕攻击、保护空间资源为主要目的空间攻防已成为空间军事化、空间武器化的重要发展方向.
卫星识别是实施天基空间对抗的一项关键技术.随着空间目标抵近技术的日益发展,已使得利用天基平台进行目标近距离的光学探测与识别成为可能[1-4],深入研究相应的识别算法对提升天基空间对抗能力具有重大意义.目前国内外在目标探测识别方面已开展了大量工作,但研究多集中在针对远距离观测过程中的卫星分辨及对卫星类型的识别方面,由于远距离观测多为点状目标,无结构、形状、纹理等信息,因此多是将目标的运动特征、光谱特征以及辐射特性作为识别依据进行算法设计(如文献[5-7]).文献[8-10]中研究了近距离观测下估计目标星姿态与几何结构的识别算法,但它们都是针对整星的运动特征和几何结构的全局识别,尚未针对卫星的本体、帆板等局部构件提出相应的分类辨识特征.从现有文献来看,针对在轨成像条件下卫星本体、帆板、天线等卫星局部的光学识别方法研究未见报道.因此,研究卫星局部的识别方法,对天基目标识别以及满足局部操作的需求显得尤为重要.
本文在分析典型卫星局部构件物理特征的基础上,研究它们的参量化表征方法,构建用于分形典型构件的聚类参量集,并建立基于多特征加权组合的分形聚类模型,据此提出相应的识别方法,同时针对空间目标在轨成像过程中的目标局部变形、互遮挡、像质退化等特殊性问题,建立目标识别算法框架与流程,提出基于单帧与多帧序列图像的目标识别算法,并进行算法的仿真与半物理实验验证.
1 融合多特征的卫星构件分形聚类模型
1.1 卫星构件的物理特征分析
典型卫星局部构件主要包括本体、太阳帆板、天线及搭载在本体表面或内部的空间相机、激光反射器、发动机喷口等,其物理特征见表1.

表1 典型卫星构成及其物理特征
考虑到空间相机、激光反射器等有效载荷或隐藏在本体内或形态差异大或辐射特性与其他构件存在显著差异(可采用红外手段进行直接识别),因此本文的研究重点为本体、帆板和天线构件的识别.
图1 (a)、(b)所示为国外某预警卫星及其轮廓提取结果.由表1和图1可见:卫星本体、帆板、天线分别显现出特定但不唯一的几何形态、相对位置关系、尺寸、灰度分布等物理特征,因此很难选定某个单一特征来判别目标所隶属的构件类型.
在近距离卫星目标观测中,构件的这些可见光形式特征是可被光学识别的,因此根据卫星的先验信息,研究本体、帆板、天线物理特征的参量化表征方法,并寻找能够最大程度分形聚类各类构件的参量组合,是准确识别卫星局部构件的关键问题.
1.2 分形聚类特征的参量化表征
经上述分析可知,不同构件表现出不同的几何形状、相对关系、尺寸等物理特征,这些特征可作为目标分形聚类的依据.

图1 典型卫星及局部构件特征示意
几何形状主要包括平行四边形/矩形/正方形、平行六边形、椭圆/圆和不规则多边形.本文采用角点、直线、椭圆检测算子提取封闭图形局部轮廓,再结合边线数量、斜率大小等特征参量描述待识别目标的几何形状[11-13];采用面积、边长等特征参量描述待识别目标尺寸;相对关系包括生长、连接、共线和多面体关系.生长关系是指一个较大封闭图形边上/形内存在较小封闭图形.连接关系是指两个封闭图形尽管不存在直接交/连关系,但可找到它们间的连通区域.共线关系是指两个相邻封闭图形存在共用边,存在多组有交点的共线关系则是多面体判别的重要依据.本文采用封闭图形间的形心位置、线条相交和重合等特征参量来判别相对关系;灰度分布特征分为均匀和非均匀的平面/多面体.非均匀的平面体可认为存在其上小构件、规则贴片或不规则包裹.本文采用凹凸面/多面体、规则纹理面/多面体及非规则纹理面/多面体等特征参数描述待识别目标的灰度分布.
1.3 多特征参量加权组合的分形聚类模型
结合分形聚类特征的参量化表征,根据典型卫星本体、帆板和天线先验信息,构建用于判别各种构件的分形聚类参数集及相应的判别权重值,见表2~4所示.
表4 卫星天线分形聚类特征及权重系数
Tab.4 Fractal clustering features and weight coefficients of the antenna

分形聚类特征分形特征的参数化描述权重外轮廓形状满足特定对象的先验知识,弧+多边形、圆形、椭圆形等,边数很多的多边形0.30相对形心位置≥特定对象先验知识,从小到大排后40.15面积占比≤特定对象先验知识,从小到大排前30.20长度占比≤特定对象先验知识,从小到大排前30.20连接关系与本体存在连接或生长关系0.05灰度分布均匀0.10
在此基础上,通过计算待识别目标特征与各构件类同一特征的匹配性概率,并根据该目标隶属于各构件类的匹配性概率的高低排序,即可实现目标的分形聚类与识别.建立的融合多种特征参量加权组合的卫星本体、帆板和天线分形聚类模型为
(1)
式中:PL为待识别目标隶属于各构件类的匹配性概率;λk为该构件类特征参数权重值,且满足:∑λk=1;Sign(λk)为待判别目标特征是否与构件类的第k项分形聚类特征相匹配的判别函数,对于隶属于该构件类的特征参量赋予相应权重.λk的初值首先是依据卫星构件先验知识进行初步确定,如本体相对形心位置最小是本体区别其他构件的最显著特征,因此其在本体判别中对应的权重值最大.再结合大量包含不同光照、成像尺度、方位、姿态变化的目标星仿真图像识别结果进行优选.λk的最终值是在优选后的λk初值的基础上,进一步结合粒子群算法[12],以识别算法在更完备图像扩展源实际应用中的识别概率为依据进行迭代优化的结果.事实上,粒子群算法是一种基于群智能的优化方法,它能够通过群体内部个体之间的交互协同与合作,使整个群体在复杂空间中探寻全局最优化区域.而且不会因个体故障影响整个问题的求解,能够确保系统具有很强的鲁棒性,因此适用于本文基于大量复杂多样性样本(包含不同尺度、相对方位、姿态变化等),以识别概率全局最优为目标,实现多种特征参量最优化迭代求解的需求,而且能够有效解决目标严重变形、遮挡等情况引起的某个聚类特征项在相应帧图像识别中失效带来的权重求解不适定的问题.
2 基于分形特征的目标识别算法
在分形聚类建模的基础上,针对单帧图像与多帧序列图像建立目标识别框架与流程,提出相应的识别算法,并以典型卫星为例,说明构件分形聚类与目标识别的具体过程.
2.1 识别算法
目标识别算法框架与流程如图2所示.单帧图像识别算法由预处理、图像分割、分形特征提取等4步组成.首先,考虑到在轨成像系统所致图像模糊、噪声等像质退化对目标识别的影响,采用频域滤波[15]与Gamma算法[16]进行图像预处理,目的是消除原始图像噪声并增强图像的对比度;然后,通过图像分割提取待识别目标的图形轮廓.图像分割是根据灰度直方图特性选择阈值,再进行二值化与连通区域提取[15];通过目标分形特征提取获得封闭图形的分形聚类特征参量.该过程是利用轮廓点的有序性、唯一性,通过一定顺序提取轮廓点,本文提出了一种基于轮廓跟踪的分形特征提取算法,分别实现基于轮廓的直线、角点、椭圆、多边形等目标几何形状的快速、准确提取,从而解决构件变形所致的特征误匹配问题,同时提高了搜索效率;最后,利用卫星构件的分形聚类模型,通过基于分形特征匹配完成目标识别.
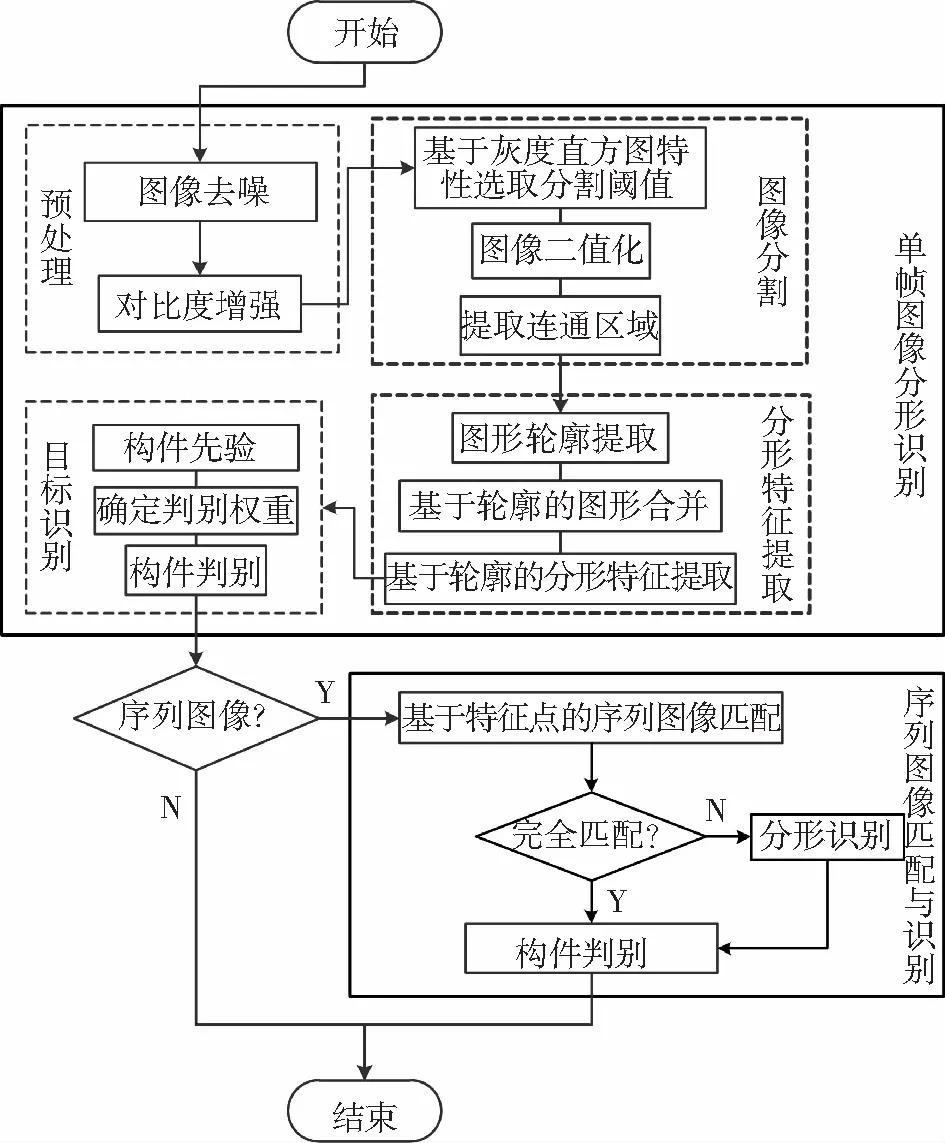
图2 目标识别算法框架与流程
考虑到单帧图像识别易受卫星姿态与太阳照射角度的影响,待识别目标在图像中表现为几何形状的变形及遮挡,本文在单帧图像识别基础上,利用连续的多帧序列图像来保证所有待识别构件在整个识别过程中均出现,并避免由于某个构件被遮挡而造成其他目标识别失效的情况.考虑到同一构件在连续帧图像中通常对应多个同名像点,因此结合序列图像帧间特征的匹配关系,提出基于多帧序列图像的目标识别算法.通过特征匹配不仅可以实现已识别目标结果的进一步确认,还可以避免被遮挡构件对其他目标识别产生的影响,进一步提高识别算法的抗遮挡能力,从而有效地解决卫星姿态发生大角度变化时导致的构件变形与遮挡引起的识别概率下降问题.匹配方法为:首先利用单帧识别算法对首帧图像进行目标分形识别,将已完成识别的图形作为特征域;然后利用Surf算法[17]提取相邻帧图像的全局特征点,并对特征点进行平行度筛选;而后提取共面特征点;最后通过进一步筛选特征点间距离不存在突变的点,获得匹配特征点.当连续多帧图像帧间特征完全匹配时即可完成目标判别,否则重新进行单帧图像的分形识别.
2.2 分形聚类模型权重求解与识别
以图1(a)典型预警卫星为例,说明分形聚类模型权重求解与目标识别过程.如图1(a)所示,从不同观测角度来看,该星先验包括:①存在性.本体、2个主天线和帆板;②外形.本体为立方体,轮廓为平行多边形,帆板为平行四边形,天线为椭圆或不规则形状;③本体形心距卫星形心最近;④大小.帆板(>40%)>主体(>10%)>天线(<10%);⑤连接关系.帆板、天线与本体连接,帆板、天线独立.帆板、天线在本体外,呈十字分布;⑥灰度分布.帆板和天线表面平滑,本体表面包含小构件,非平滑.
首先通过图像分割提取图像中卫星局部目标的图形轮廓,各封闭图形的分形聚类特征描述见表5.
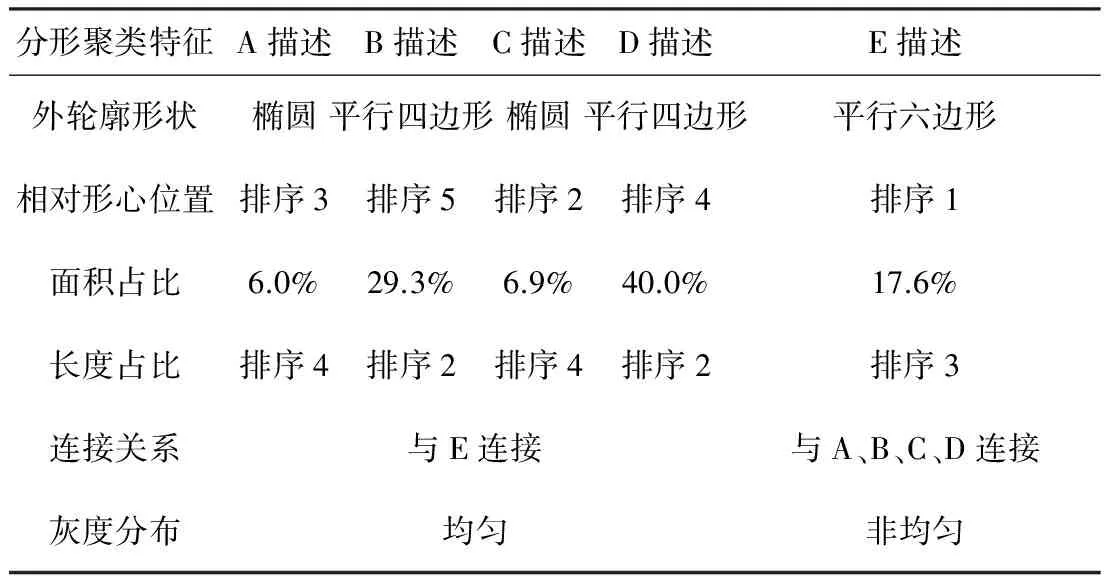
表5 分形聚类特征描述
然后选定初始权重,利用卫星本体、帆板和天线构件分形聚类模型对各封闭图形进行目标识别,以识别结果统计最优为目标,迭代解算模型中各分形聚类特征对应的权重值,解算结果见表2~4.
利用模型权重系数和式(1)计算待识别目标隶属于各构件类的匹配性概率,计算结果见表6.根据匹配性的高低排序即可得出目标识别的最终结果:A和C为天线,B和D为帆板,E为本体.
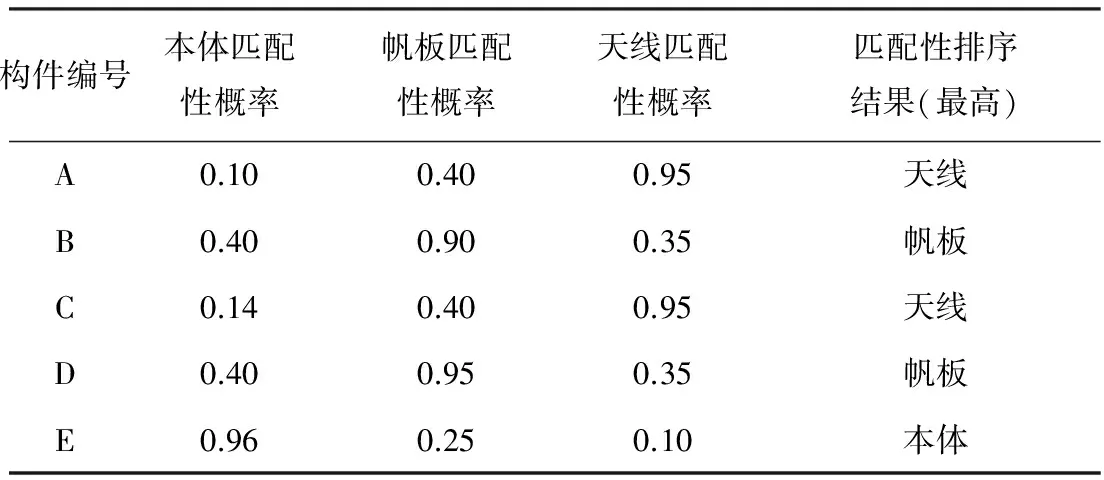
表6 匹配性概率与目标识别结果
3 识别算法的实验验证
3.1 仿真实验及结果分析
仿真数据源包括:①卫星1.哈勃太空望远镜(HST),长13.3 m,直径4.3 m,包含两个长11.8 m、宽2.3 m的帆板、两个抛物面型天线(如图3(a));②卫星2.跟踪与数据中继卫星(TDRS)具有两个直径为4.6 m的展开式天线、两个长20.7 m的帆板(如图3(b));③卫星3.国外某预警卫星(如图1(a));④卫星4.基于光学特性物理仿真生成的典型低轨成像卫星(SAT)(如图3(c)所示).该星具有1.5 m正方体的本体、6个长3 m、宽1.5 m的帆板,其中位于中间部位的帆板呈现出不规则的几何形状.卫星表面材料假定为灰体,反射率为50%.
每幅图像加入MTFN(奈奎斯特频率下的传递函数)在[0.05, 0.15]之间的高斯模糊、SNR在[2, 7]之间的高斯白噪声,模拟相机光学系统、探测器、成像电子学与平台抖动引起的像质退化.通过改变卫星轨道根数、姿态角以及观测星与目标星的相对方位,模拟两星在相对姿态[-90°, 90°]、相对距离从10~3 km的不同逼近、绕飞与悬停轨道状态,从而生成包含各种构件变形、遮挡情况的目标星图像.
图4分别给出了卫星局部构件变形、构件遮挡、较严重模糊、高噪声水平(SNR=5)等情况下的单帧图像及逼近、伴飞状态下成像获取的序列帧图像的目标分形聚类与识别结果.限于篇幅,仅以图4(b)卫星和图4(f)卫星50帧序列图像的目标识别结果(见表7、8)为例,说明识别算法性能.

图3 典型卫星在轨示意

图4 识别结果(图中绿色标记的数字代表待识别目标的编号)
Fig.4 Results of the target identification(The targets to be identified are marked by green numbers)
注:彩图见电子版(http://hit.alljournals.cn)(2016年第10期)

表7 图4(b)单帧图像目标识别结果

表8 图4中第50帧序列图像目标识别结果
从图4、表7~8可看出:1)构件变形与互遮挡会引起目标分形特征匹配性概率的下降,但只要构件目标未被完全遮挡,采用单帧算法仍可对各构件进行准确识别,这说明了算法采用多种分形聚类特征联合辨识的有效性;2)像质退化会影响目标分形聚类结果(如图4(c)、(d)中的天线),但当原始图像SNR>5时,在对比度很低甚至影响到人眼判读的情况下(如图4(e)),采用本文算法仍可实现对目标构件的准确识别,多帧识别概率优于95%.这也说明了算法采用预处理及多帧序列图像分形特征匹配策略的有效性.
3.2 地面半物理实验及结果分析
利用卫星缩比模型、太阳模拟器、光学探测器、三维电控转台,设计并搭建半物理仿真实验平台(如图5所示),利用实验数据进一步说明算法在卫星局部识别实际应用中的有效性.
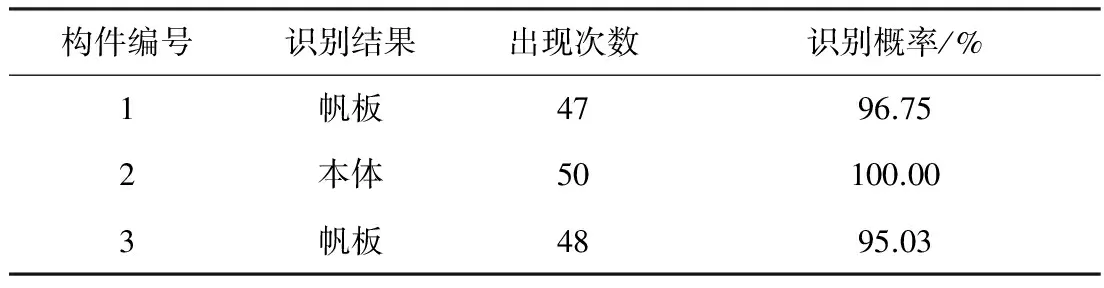
目标选用伽利略卫星40∶1缩比模型,包含本体与太阳帆板,几何尺寸分别为1 200 mm ×1 100 mm×2 700mm、6 500 mm×2 700 mm×25 mm,本体材料为F46聚酯薄膜,帆板材料为SR107白漆(背面)、帆板GaInP2/GaAs/Ge(正面)、有机黑漆(侧面),与真实目标的结构与表面材料属性相同.为真实模拟空间目标的背景环境,选用太阳模拟器作为背景模拟光源.用太阳模拟器以某一角度照射缩比模型,使用光学探测器与电控转台从不同角度进行拍摄以获取不同入射角及反射角情况下的目标图像.改变太阳模拟器的照射角度,以实现更加丰富的角度模拟.改变拍摄距离以模拟不同观测距离的成像结果.光学探测器采用Nikon公司的AF-S600mmF4DII型高品质镜头和DTA公司生产的ICAM型CCD器件.此外,为模拟空间光学成像的图像质量退化,在实验数据中加入高斯模糊与噪声.图6和表9给出了连续第50帧图像的目标分形聚类与识别结果.
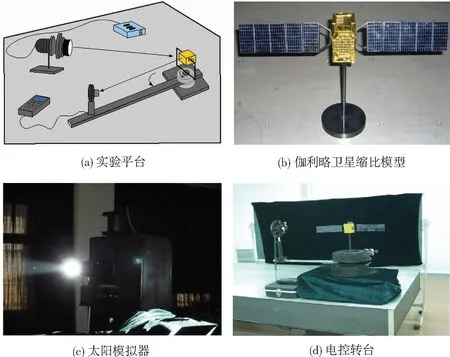
图5 半物理实验平台与装置

图6 多帧序列图像目标分形聚类与识别
构件编号识别结果出现次数识别概率/%1帆板4796.752本体50100.003帆板4895.03
从图6和表9中可以看出,在帆板与背景的对比度很低,且图像中包含较严重模糊(MTFN仅为0.06)与噪声(SNR仅为5)的情况下,目标识别算法仍可对卫星局部构件进行准确识别.其中,本体识别概率达到100%,帆板识别概率优于0.95.
4 结 论
1)通过分析典型卫星的物理特征,提出了卫星本体、帆板、天线的分形聚类特征,并结合聚类特征的参量化表征,根据典型构件的先验信息,构建了基于分形特征参量加权组合的聚类模型;
2)针对空间目标光学在轨成像的像质退化、几何变形、遮挡等特殊性问题,建立了基于单帧与多帧序列图像的目标识别框架与流程,从而提出了相应的识别方法与算法;
3)为实现识别算法的性能分析与验证,以4种不同典型卫星为应用实例进行了算法的仿真实验验证,同时利用伽利略卫星缩比模型进行了半物理实验.实验结果表明:在目标与背景对比度很低、SNR仅为5,且构件存在较严重变形与遮挡的情况下,该算法仍能够准确识别卫星本体、帆板与天线,且识别概率优于0.95.
[1] SHARMA J. Space-based visible space surveillance performance[J]. Journal of Guidance, Control, and Dynamics, 2000, 23(1): 153-158. DOI:10.2514/2.4503.
[2] Payne T P, Morris R F. The space surveillance network(SSN) and orbital debris[J]. Advances in the Astronautical Sciences, 2010, 137(4): 2010.
[3] FLOHRER T, KRAG H, KLINKRAD H, et al. Feasibility of performing space surveillance tasks with a proposed space-based optical architecture[J]. Advances in Space Research, 2011, 47(6): 1029-1042. DOI: 10.1016/j.asr.2010.11.021.
[4] ZHANG Haopeng, JIANG Zhiguo, ELGAMMAL A. Vision-based pose estimation for cooperative space objects[J]. Acta Astronautica, 2013, 91: 115-122. DOI:10.1016/j.actaastro.2013.05.017.
[5] XU Yonghui , ZHANG Jihui, WEI Yi. Recent patents on real-time deep space target track system based on Dual-DSP[J]. Recent Patents on Computer Science, 2013, 6(3): 227-232. DOI: 10.2174/22132759113066660012.
[6] TANG Jia, GAO Xin, JIN Gang. Dim and weak target detection technology based on multi-characteristic fusion[C]//Proceedings of the 26th Conference of Spacecraft TT&C Technology in China. Berlin, Heidelberg: Springer- Verlag, 2013: 271-277. DOI:10.1007/978-3-642-33663-8_27.
[7] HOU Wang, LONG Gucan, LEI Zhihui, et al. The small target detection based on maximum likelihood estimation and spot detection operator[C]//Proceedings of SPIE 9142. [S.l.]: SPIE, 2014: 914207(1-13). DOI:10.1117/12.2054032.
[8] DU Xiaodong, LIANG Bin, TAO Yanbo. Pose determination of large non-cooperative satellite in close range using coordinated cameras[C]//Proceedings of the 2009 International Conference on Mechatronics and Automation. Changchun: IEEE, 2009, 3910-3915. DOI: 10.1109/ICMA.2009.5244890.
[9] ZHANG Haopeng, JIANG Zhiguo, ELGAMMAL A. Satellite identification and pose estimation using homeomorphic manifold analysis[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(1): 785-792. DOI: 10.1109/TAES.2014.130744.
[10]CROPP A, PALMER P, MCLAUCHLAN P. Estimating pose of known target satellite[J]. Electronics Letters, 2000, 36(15): 1331-1332. DOI: 10.1049/el:20000950.
[11]RANGARAJAN K, SHAH M, VAN BRACKLE D. Optimal corner detector[J]. Computer Vision, Graphics, and Image Processing, 1989, 48(2): 230-245. DOI:1 0.1016/S0734-189X(89)80039-8.[12]BISWAS R, SIL J. An improved canny edge detection algorithm based on type-2 fuzzy sets[J]. Procedia Technology, 2012, 4: 820-824. DOI:10.1016/j.protcy.2012.05.134.
[13]KIM E, HASEYAMA M, KITAJIMA H. Fast and robust ellipse extraction from complicated images[C]//Proceedings of the IEEE International Conference on Information Technology and Applications. Bathurst, Australia: IEEE, 200: 357-362.
[14]KENNEDY J. Particle swarm optimization[M]. Encyclopedia of Machine Learning. New York: Springer US, 2010: 760-766. DOI:10.1007/978-0-387-30164-8_630.
[15]JIANG Chao , GENG Zexun, BAO Yongqiang, et al. Analysis the application of several denoising algorithm in the astronomical image denoising[C]//Proceedings of SPIE 9142. SuZhou, China: SPIE, 2014: 91421N(1-7). DOI:10.1117/12.2054427.
[16]JIANGA G, WONGA C Y, LIN S C F, et al. Image contrast enhancement with brightness preservation using an optimal gamma correction and weighted sum approach[J]. Journal of Modern Optics, 2015, 62(7): 536-547. DOI: 10.1080/09500340.2014.991358.
[17]AL-AMRI S S, KALYANKAR N V, KHAMITKAR S D. Image segmentation by using edge detection[J]. International Journal on Computer Science and Engineering, 2010, 2(3): 804-807.
[18]GUO Fei, LUO Xiao, LIU Yi. Research on feature extraction and match method based on the surf algorithm for mobile augmented reality system[C]//International Industrial Informatics and Computer Engineering Conference. [S.l.]: [s.n.], 2015, 615-519. DOI:10.2991/iiicec-15.2015.140.
(编辑 张 红)
Optical identification method of space typical targets based on combined multi-feature metrics
ZHI Xiyang, HOU Qingyu, ZHANG Wei, SUN Xuan
(School of Astronautics, Harbin Institute of Technology, Harbin 150001, China)
This paper proposes a new method based on combined multi-feature metrics in order to meet the requirements for identification of satellite local targets. Firstly, we analyze the local physical characteristic of satellite, and construct the local component fractal clustering parameter sets of the fusion morphology multi-feature metrics. Then, a component-clustering model is formulated based on weighted combination of clustering features. Consequently, an optical identification algorithm is proposed to deal with the problems of image degradation and partial occlusion in optical imaging of space targets. Based on the recognition probability in its practical application, the efficiency and robustness of the recognition algorithm is improved by using optimal weighting coefficients in the iteration of particle swarm optimization algorithm. Finally, using four typical satellites and Galileo satellite scaled model, the performance of the identification algorithm is analyzed and verified. Experimental results show that the algorithm is able to identify the satellite component and the identification probability is no less than 0.95, in the case of low contrast, SNR being 5 and severe deformation and mutual occlusion of the components.
space target identification; satellite local; combined feature metrics; clustering model; identification algorithm
10.11918/j.issn.0367-6234.2016.10.006
2015-08-20
国家自然科学基金(61605035)
智喜洋(1982—),男,副教授,硕士生导师;
张 伟(1962—),男,教授,博士生导师
侯晴宇,houqingyu@126.com
TP751.1
A
0367-6234(2016)10-0044-07
