考虑轨道集肤效应的地铁牵引供电系统故障测距方法

贾明泽

（北京交通大学电气工程学院，北京 100044）

考虑轨道集肤效应的地铁牵引供电系统故障测距方法

贾明泽

（北京交通大学电气工程学院，北京 100044）

近些年来，地铁牵引供电系统的稳定运行以及故障时的快速处理显得越来越重要，这就要求牵引网一旦发生故障能够准确的故障定位。本文在总结现有方法的基础上，着重分析了集肤效应对故障测距的影响，得出了故障电流时间常数与轨道单位电感与电阻的关系，基于以上分析，提出了在考虑集肤效应影响下，通过含有遗忘因子的最小二乘法的系统辨识得到轨道阻抗参数，然后采用模拟退火—最小二乘混合测距法完成测距。并通过Matlab/Simulink中搭建的仿真模型故障数据与某市的实测故障数据验证了方法的可行性以及准确性。

牵引供电；集肤效应；最小二乘法；故障测距

随着轨道交通的快速发展，牵引供电系统的安全可靠越来越引起人们的关注。距统计广州地铁 2号线从2003年开通至2009年间发生1500V馈线开关跳闸38次，造成多起旅客滞留事件，其中多为车辆问题造成的瞬时性故障，对接触网（轨）的烧熔为日后故障埋下隐患［1］但因未造成停电事故，传统的人工寻线对此类故障效果不大，因此通过故障信息实现快速准确的自动故障定位计算不仅可以保障地铁运行的快速恢复，更可以尽早发现隐患，提高了其日后的运行可靠性。现有的地铁故障测距算法的研究都是借鉴已有的电力系统输电线路故障测距的方法。输电线路的故障测距方法按提取信号的不同分为基于工频量和基于行波的故障测距两类［2］。基于工频量的故障测距方法又可分为单端法、双端同步法、双端不同步法。借鉴这些方法，在地铁牵引供电系统中，研究人员提出了基于轨电位的微分方程法［3］、基于SCADA的区段定位法［4］、基于贝瑞龙模型的电压分步法以及基于回路电压的最小二乘法等算法［5］等。

这些算法在不考虑集肤效应对线路参数影响下仿真验证可以实现精度较高的故障测距，但当考虑集肤效应时，由于以上算法中都使用了接触网和走行轨的阻抗参数，而这些参数在短路过程中由于受集肤效应的影响，变化很大，造成测距方法误差增大、甚至失效。因此，必须针对地铁的以下几点特殊性，考虑故障测距问题:①接触轨和走行轨横截面积大且形状不规则，磁导率高，决定了线路参数受集肤效应影响大，线路参数难以测定；②线路结构复杂，道岔、道辙鱼板尾连接等阻抗不连续点多，无法使用行波测距法；③地铁供电系统中设置了大电流脱扣保护、电流增量保护、钢轨电位限制器等复杂保护控制，动作迅速，可用暂态数据较少。基于以上三点本文提出在考虑集肤效应的影响下，使用递推最小二乘法辨识线路时间常数，结合时间常数与轨道参数的关系，得到故障距离的双端同步故障测距方法。

1 牵引供电系统故障介绍及轨道集肤效应的分析

1.1 牵引供电系统故障介绍

地铁牵引供电系统主要包括牵引变电所和牵引网两部分组成，地铁牵引网在绝大部分情况下采用双边供电或大双边供电［6］。

由现场的运行经验，牵引供电系统的故障主要有过电压故障、短路故障、过负荷故障。最常见且危害最大的是短路故障［7］。短路故障一般可分为金属性故障和非金属性故障，其中金属性故障更为常见，且多为瞬时性故障，重合闸一般成功，但接触线线面会出现拉弧烧伤痕迹，增加了日后运行的磨损与断线的可能性［1］。

1.2 轨道集肤效应的分析

导体中有交流电或者交变电磁场时，导体内部的电流分布并不均匀，这种现象称为集肤效应［9］。集肤效应对轨道阻抗的暂态变化起决定性的作用。因此，集肤效应对故障测距的影响不能忽略。考虑集肤效应的轨道阻抗计算可以使用有限元法，但计算量大且计算复杂，本文使用钢轨的等周长圆柱模型［9］，研究表明［3-10］对短路故障电流正弦拟合分析得到故障电流初始变化与 10～25Hz的交流电流近似相等，且等周长圆柱在短路电流频率大于5Hz时的阻抗频率特性与钢轨基本重合。因此使用等周长模型计算的暂态阻抗较为准确。

轨道的阻抗包括内阻抗和外电感，外电感与三轨及走行轨的位置距离有关，内阻抗采用等周长圆柱模型来计算接触轨与走行轨的阻抗得到公式［9］

式中，ω为角频率；R2为等效圆柱体半径；σ为电导率；μ为磁导率。

由公式可知阻抗与频率、轨道等周长模型的半径、电导率、磁导率有关，模型的半径在钢轨型号一定时为一个定值，铁轨在电流为500～800A时会出现磁饱和现象，列车运行电流2000A左右，频率主要以 0～2Hz的低频为主，而短路电流很快上升到大于800A，即正常运行与短路时可把铁轨的磁导率看作定值［11］。导体的电导率与导体的温度有关［12］，如下

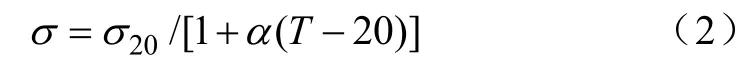
式中，σ20为 20℃时的电导率；T为温度；α为电阻率温度系数，这里取铁的α值0.00651，牵引供电系统导体变化范围一般在15～65℃。定义单位导体电感与电阻之比为导体的时间常数。则由上式可得图1。

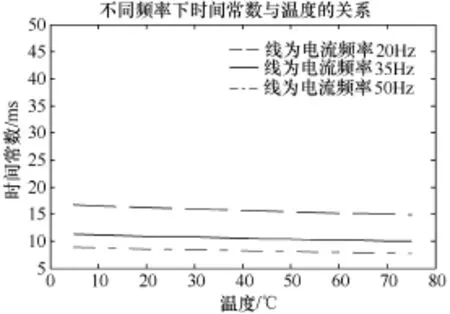
图1 不同频率下时间常数与温度的关系

可知温度对导体的时间常数的影响很小，可认为相同电流频率不同温度下的电导率近似相等。因此在钢轨型号固定后，由式（1）可知，钢轨的电阻电感近似主要受流过导体的导体的频率影响，计算结果见表1。

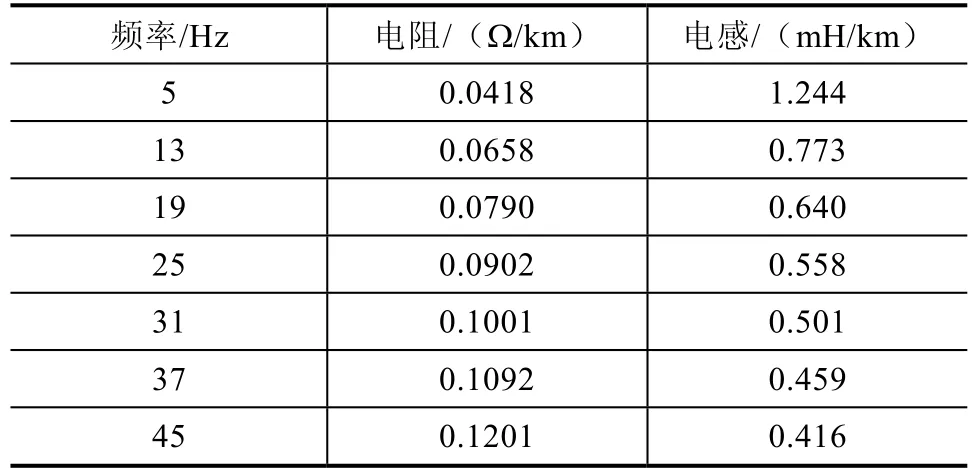
表1 轨道频率与电阻电感的关系表

可见随着频率的增大，电感逐渐减小，电阻逐渐增大，时间常数逐渐减小，分别对电感、电阻与导体的时间常数做曲线拟合，得到电阻、电感与时间常数的关系式，拟合结果为

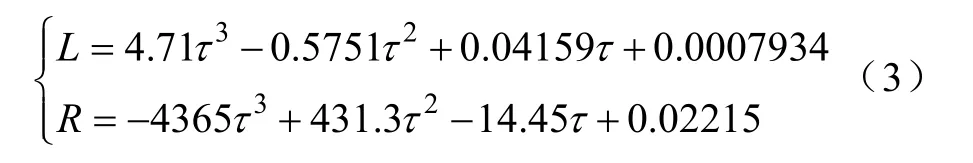
在极短的时间内可认为时间常数变化很小，鉴于以上分析，再考虑集肤效应的影响下，通过求1ms内单位导体的时间常数，即可求对应时刻的导体的单位阻抗，使准确测距成为可能。

2 测距算法的分析

由上节分析可得准确的辨识时间常数是故障测距成功的基础，系统参数模型的辨识方法根据工作原理可分为最小二乘法、梯度矫正法和极大似然法三种方法。其中最小二乘法原理简明、收敛较快、易于理解、易于编程，在系统参数估计中已被广泛应用。考虑到应用于故障测距的系统识别算法处理数据较大且为轨道的阻抗参数在短路过程中为变化的，因此使用了带遗忘因子的递推最小二乘法（forgetting factor recursive least square）。在慢时变系统中带遗忘因子的最小二乘法可以克服数据饱和现象，在递推最小二乘法中，取性能指标为

式中，λ为遗忘因子。由上式推导含有遗忘因子递推最小二乘参数估计的公式为

初值为

式中，α为充分大的正实数；ξ为零向量。

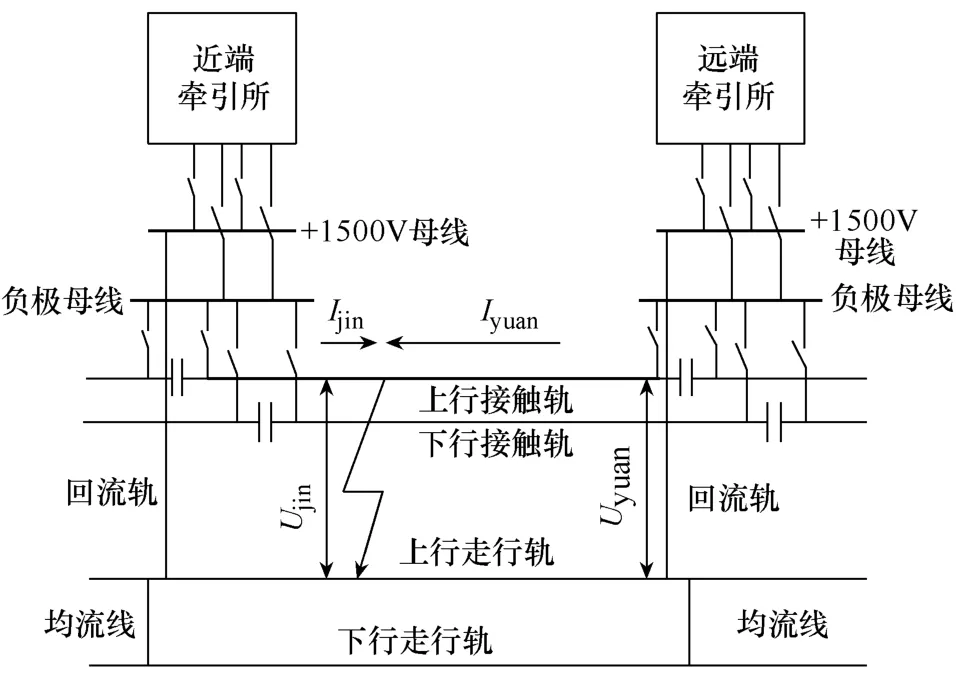
图2 牵引网短路故障示意图

对应于图2中发生短路故障，分别由牵引变电所两侧的电压电流数据计算沿线电压分布，得到的故障点处电压相等，即

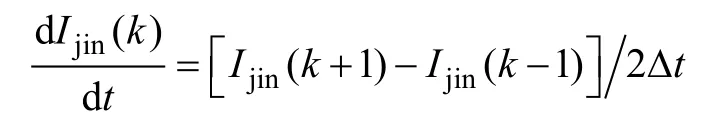
式中，Δt为采样周期。而Rjin、Ljin、Ryuan、Lyuan分别为故障点到近端牵引所的三轨的单位电阻和电感以及故障点到近端牵引所的三轨的单位电阻和电感，lf为故障点距近端牵引所的距离，lall为两牵引所的距离。对式（6）做变换得

令

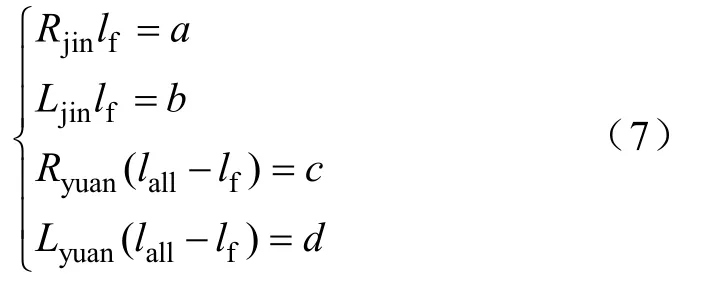
则上式变为

利用采样所得数据，运用 FFRLS对上式中 a，b，c，d进行参数辨识，由

得到近端与远端的三轨时间常数，代入由上节得到的阻抗与时间常数的近似拟合曲线得到采样时刻故障点两侧的单位阻抗值。但这一数值由于是通过参数辨识后代入拟合函数得到，使得计算阻抗与实际阻抗存在误差。为实现准确测距，故障点两侧的导体阻抗值设为在包含计算阻抗值的一定范围内，即

模拟退火算法具有良好的全局寻优能力，能够克服最小二乘算法对初值敏感的问题，但在搜索后期效率较低导致搜索的精度和稳定性均不高［13］。而最小二乘算法在初值良好时收敛速度及其精度都非常高，可以弥补模拟退火算法的缺点。因此，结合模拟退火算法全局寻优能力与最小二乘法在初值良好时快速收敛能力［14］，可实现两者的互补。由上文可知，通过参数辨识可得某一时刻的导体的阻抗值，在一个极小时间段内（取1ms），认为阻抗不变，通过对上式在前式约束条件下的基于模拟退火和最小二乘的混合优化算法即可得到故障测距的结果。综上所述，故障测距算法具体流程如下:

1）采集故障点两侧的电压电流值，计算电流变化率，初始化时间t为零。

2）将 1）中的数据送入基于 FFRLS参数辨识方法中，得到故障后保护动作前任意时刻三轨的阻抗计算值。

3）判断t到t+1s内是否保护动作，若保护动作则跳至6）。若未动作则取t到t+1内的电压、电流与电流变化率与的计算阻抗值。带入不等式，得到约束条件。

4）利用模拟退火法搜索新状态，作为最小二乘法的初值。

5）运用最小二乘法计算，若收敛，则将得到故障距离lf存入数组L中，返回3），若不收敛则返回4）。

6）对所得的数组L中数据求均值，作为故障测距的结果返回。

3 算法的仿真和实例验证

3.1 算法的仿真验证

为验证本文所提出的测距算法，使用 Matlab/ Simulink搭建双边供电的直流牵引系统模型。采用1500V三轨供电，考虑与故障点距离最近的4个牵引变电站，牵引变电站间距离为 3km，牵引变电站采用24脉波整流电路，采用文献［13］的数据，三轨外电感0.724mH/km、走行轨外电感为0.602mH/km，为模拟内阻抗，设置仿真中的阻抗为时变阻抗，参考表1中的数据与实际的故障发生后近端电流正弦拟合后频率较大的结论，故障点到近端和远端牵引所阻抗随时间变化的关系设为

式中，t为时间，s；电阻单位为Ω/km，电感的单位为mH/km。采用前文所提算法对不同故障距离，不同短路阻抗的故障测距结果见表 2，其中误差百分比为误差占牵引所距离全长的百分比。

表2 不同短路电阻、不同故障距离的故障测距结果

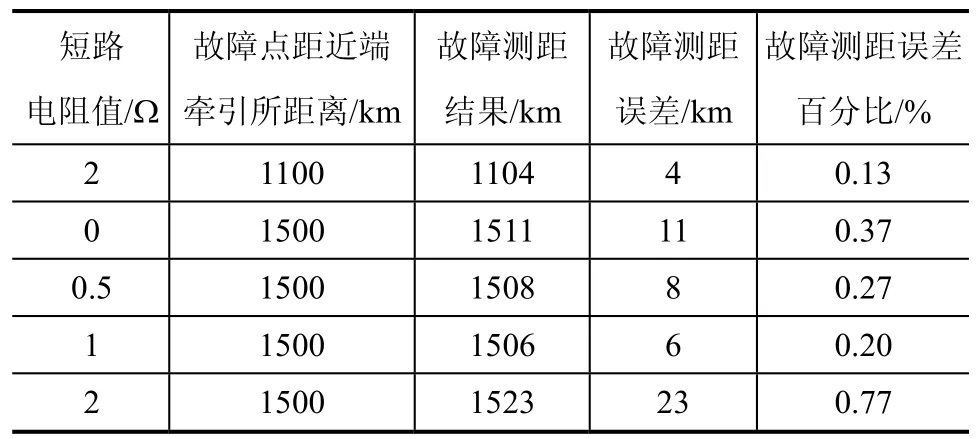
（续）

3.2 算法的实例验证

本文采用某市五号线的一次实际短路故障验证算法的可行性，故障为高架段隔音板脱落搭接在接触轨和接地扁铝上，导致1500V接触轨对接地扁铝短路。图3所示为故障后两侧牵引所跳闸开关的录波波形，近端大电流脱扣保护动作，远端ΔI保护动作。

图3 某市1500V接触轨对地短路跳闸开关录波波形图形图

实际故障距离近端牵引所 1109m。距离远端牵引所 2499m，将故障录波的数据，送入本文测距算法做的Matlab程序，计算故障点距离近端1127m，误差18m，误差长度占全长的0.6%，基本准确实现测距的要求。

4 结论

1）介绍了直流牵引供电系统的故障分类，分析了集肤效应的影响因素，计算得到不同频率下轨道的电感和电阻与轨道值，通过拟合得到阻抗与时间常数的关系。

2）通过 FFRLS实现了对时变的电阻电感的参数估计，利用拟合曲线，得到了使用优化算法的故障测距的初值与变量上下限。

3）通过模拟退火—最小二乘混合算法进行故障测距，仿真显示该测距方法不受故障距离与短路电阻的影响，有较好的测距精度。结合实例再次验证了算法的可行性。

［1］喻展.地铁 1500V直流开关跳闸故障处理［J］.都市快轨交通，2010，23（2）：106-108.

［2］胡婷，游大海，金明亮.输电线路故障测距研究现状及其发展［J］.电网技术，2006，30（S1）：146-150.

［3］张勋.DC1500V牵引供电系统故障测距研究［D］.成都：西南交通大学，2014.

［4］杨莉莉.DC1500V三轨供电系统直流馈线保护研究［D］.成都：西南交通大学，2008.

［5］王晓凯.城市轨道交通供电直流侧短路故障定位的研究［D］.北京：北京交通大学，2014.

［6］黄德胜，张巍.地下铁道供电［M］.北京：中国电力出版社，2010：117-118.

［7］韩妮乐，于勉.直流牵引供电系统短路故障浅析［J］.科技资讯，2013（8）：148.

［8］喻乐.城市轨道交通供电系统建模与直流馈线保护的研究［D］.北京：北京交通大学，2012.

［9］鲁小兵，周文卫，王元贵.基于集肤效应的地铁短路时间常数研究［J］.电气化铁道，2012（4）：41-43，47.

［10］周文卫.DC1500V牵引供电系统故障测距研究［D］.成都：西南交通大学，2014.

［11］孔玮.城市轨道交通直流牵引系统故障分析及若干问题的研究［D］.北京：华北电力大学，2005.

［12］李国欣.直流牵引回流系统分析及轨电位相关问题研究［D］.北京：中国矿业大学，2010

［13］李海锋，梁远升，王钢，等.基于模拟退火-最小二乘混合的故障测距新方法［J］.电力系统及其自动化学报，2008，20（3）：36-40.

［14］梁远升，王钢，李海锋.基于粒子群-最小二乘混合算法的参数自适应故障测距方法［J］.电力系统保护与控制，2009，37（4）：16-22.

Fault Location Method for Metro Traction Power Supply System Considering the Skin Effect of Orbit

Jia Mingze
（School of Electrical Engineering，Beijing Jiaotong University，Beijing 100044）

In recent years，stable operation and the rapid processing of the fault of traction power supply system is becoming increasingly important，which requires the traction network can be accurately located.On the basis of summarizing the existing methods，this paper analyzes the effect of skin effect on fault location .The relationship between fault current time constant and the orbital unit of inductance and resistance are obtained.Based on the above analysis，Under consideration set effects of skin effect，by containing forgetting factor least square method of system identification track impedance parameters are obtained.Then the simulated annealing the least-squares mixed ranging method measurement algorithm are presented in this paper.And the fault data of simulation model built by Matlab/Simulink and actual fault data in a city is performed to verify the feasibility and accuracy of the method.

traction power supply； skin effect； least square method； fault location

贾明泽（1990-），男，山东省济南市人，硕士研究生，主要研究牵引供电系统保护与控制。

甘肃省电力公司重点科技项目（2013101003）