高铁转向架垂向悬挂系统阻尼比的协同优化

周长城,于曰伟,赵雷雷,2

(1.山东理工大学 交通与车辆工程学院，山东 淄博 255049；2.北京邮电大学 自动化学院，北京 100876)*



高铁转向架垂向悬挂系统阻尼比的协同优化

周长城1,于曰伟1,赵雷雷1,2

(1.山东理工大学 交通与车辆工程学院，山东 淄博 255049；2.北京邮电大学 自动化学院，北京 100876)*

根据 1/4车体 4自由度垂向振动模型，利用 MATLAB/Simulink，建立了高铁转向架垂向悬挂系统阻尼比协同优化设计仿真模型；以人体振动舒适性最佳为目标，建立了阻尼比协同优化设计数学模型.在此基础上，以轨道高低不平顺作为输入激励，以一系及二系悬挂垂向行程和一系悬挂垂向动作用力为约束条件，创建了转向架垂向悬挂系统阻尼比协同优化设计方法.通过实例对阻尼比进行了优化设计，可知阻尼比的优化设计值能够改善高铁的乘坐舒适性，表明所建立的高铁转向架垂向悬挂系统阻尼比的协同优化设计方法是正确的，该研究为高铁一系和二系垂向悬挂系统阻尼比的初始设计提供了重要的理论指导.

高铁 ；转向架垂向悬挂 ；阻尼比 ；协同优化

0 引言

高铁必须具有良好的运行平稳性和安全性，否则将会影响到乘客的乘坐舒适性，甚至会引起脱轨安全事故[1].一系和二系垂向悬挂系统作为转向架悬挂系统的重要组成部分，其阻尼匹配对高铁的运行平稳性和安全性具有重要影响[2-3].然而，由于受高速列车悬挂最优阻尼匹配理论的制约，目前国内外对于高铁转向架垂向悬挂系统阻尼比的设计，大都是将一系和二系垂向悬挂系统分别单独进行研究，并根据经验在可行性设计区间选择某一一系和二系垂向悬挂系统阻尼比值，然后利用多体动力学软件SIMPACK或ADAMS/Rail通过实体建模仿真确定其设计值[4-8].利用该方法所得到的一系和二系垂向悬挂系统阻尼比值，尽管可使车辆满足当前行驶工况的要求，然而并非是转向架垂向悬挂系统的最佳阻尼匹配值.随着高铁行驶速度的不断提高，对车辆的乘坐舒适性和运行安全性提出了更高的设计要求，目前转向架垂向悬挂系统阻尼匹配的设计方法不能给出具有指导意义的创新理论.

近年来，已有许多国内外学者对轨道车辆转向架垂向悬挂系统进行了大量的研究，但这些研究主要是针对其减振器阻尼系数进行的，主要采用的方法有控制设计理论法、智能优化设计法和建模仿真优化法.例如，Sugahara Y，Takigami T等人[9-10]，分别利用H∞和LOG控制算法对轨道车辆的一系垂向悬挂系统进行研究，给出了基于控制设计理论的一系垂向悬挂系统减振器的最佳阻尼系数优化设计值；Nguyen H C，Zuo L等人[11-12]分别利用H∞和分散控制技术给出了基于控制设计理论的二系垂向悬挂系统减振器的最佳阻尼系数优化设计值；Mei T X，Kim Y G，曾京等人[13-20]，分别利用遗传算法，神经网络算法，全局优化算法，稳健性设计，多目标优化方法等给出了基于智能优化方法的一系和二系垂向悬挂系统减振器的最佳阻尼系数优化设计值；Zhang Y W，Nishimura K等人[21-22]，分别利用ANSYS软件和MATLAB软件给出了基于建模仿真的一系和二系垂向悬挂系统悬挂参数的优化设计值.虽然这些研究能够给出一系或二系垂向悬挂系统减振器的最佳阻尼系数设计值，但这些研究所建立的振动模型或仿真模型中未考虑减振器端部连接结构的弹性作用，且未曾给出具有指导意义的一系及二系垂向悬挂系统阻尼比的设计方法.

本文根据1/4车体4自由度垂向振动模型，通过高铁行驶平稳性和安全性分析，对转向架垂向悬挂系统阻尼比进行研究，并结合实例，对一系和二系垂向悬挂系统阻尼比进行优化设计.

1 1/4车体4自由度垂向振动模型

1.1 模型的建立

为了研究转向架垂向悬挂系统阻尼对铁道车辆频率响应的影响，同时，又能比较直接地反映出减振器的特性，不受到整车复杂大系统的影响，本文采用1/4车体4自由度垂向振动模型，对高铁一系及二系垂向悬挂系统阻尼比进行研究，如图1所示.其中，模型考虑了一系及二系垂向减振器的端部连接刚度，坐标原点位于各自静平衡位置处.

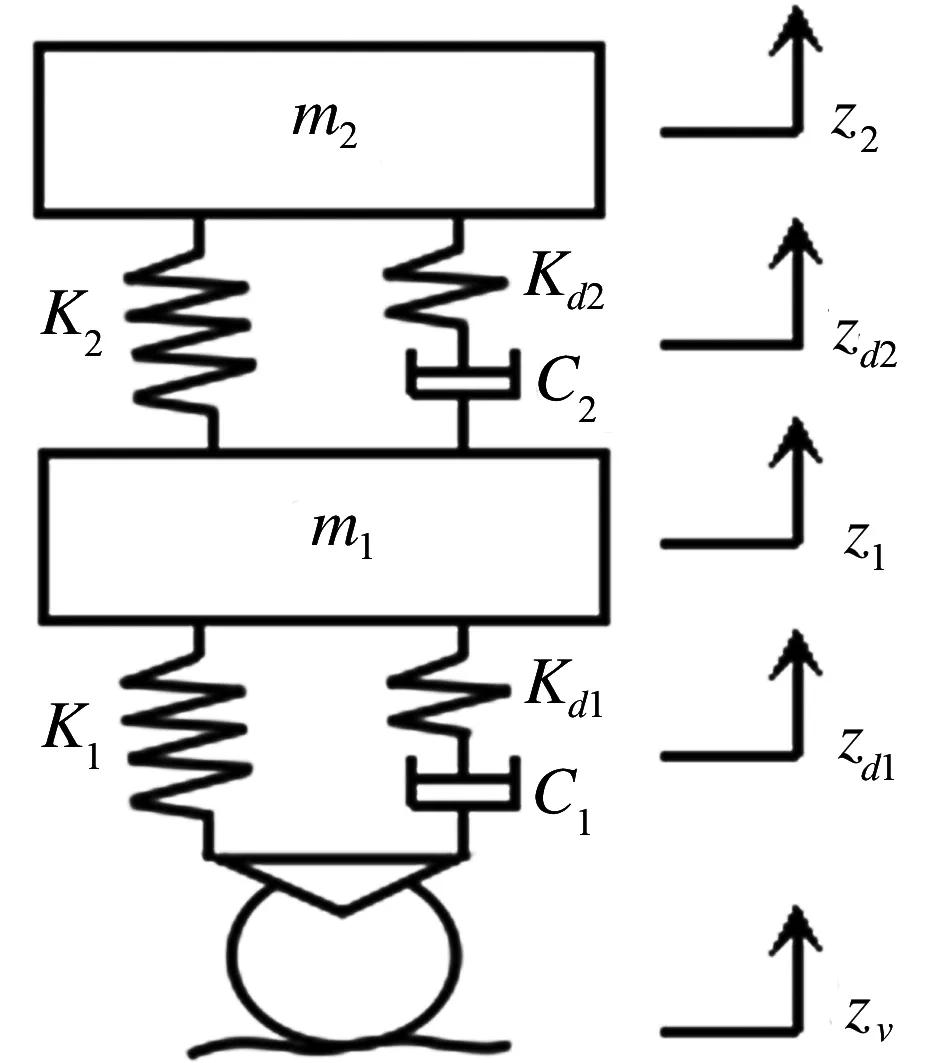
图1 1/4车体4自由度垂向振动模型

图中，m1为单个转向架构架质量的一半，m2为单节车体满载质量的1/4；K1，K2分别为每台转向架单侧一系和二系垂向悬挂弹簧的等效刚度；C1，C2分别为每台转向架单侧一系和二系垂向减振器的等效阻尼系数；Kd1，Kd2分别为每台转向架单侧一系和二系垂向减振器的端部连接等效刚度；zd1，zd2分别为一系和二系垂向减振器的活塞杆垂向位移；z1，z2分别为转向架构架和车体的垂向位移；zv为轨道高低不平顺随机输入.

1.2 车体及转向架构架垂向振动微分方程

根据1/4车体4自由度垂向振动模型，在不计轨道耦合振动作用的影响及减振器质量情况下，利用牛顿第二定律，可建立车体及转向架构架垂向振动微分方程，即

(1)

利用上述振动微分方程，可对在轨道激励下的高铁行驶振动响应及一系和二系垂向悬挂系统最佳阻尼比的协同优化设计进行研究.

2 轨道高低不平顺激扰模型

2.1 轨道高低不平顺

轨道高低不平顺是引起机车车辆产生垂向振动的主要原因.近年来，国内、外对于轨道随机不平顺已进行了大量的研究，其中应用较为成熟、广泛的主要有美国六级轨道谱和德国高速轨道谱[23].本文采用对高速轨道线路拟合程度较高的德国高低不平顺作为高铁垂向振动的轨道输入，其中，高低不平顺以空间频率形式表示的解析表达式为

(2)

式中，Sv(Ω)为轨道高低不平顺功率谱密度，Ω为轨道不平顺空间频率，Av为轨道粗糙度系数；Ωc、Ωr为截断空间频率.其中，各已知参数值如表1所示.

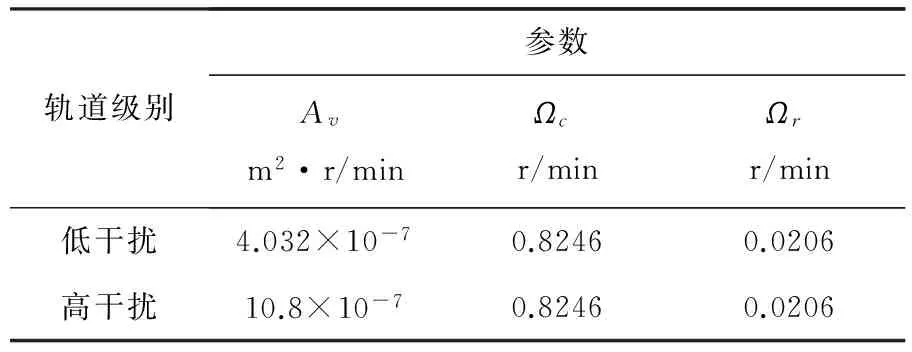
表1 德国高低不平顺参数值

其中，低干扰谱适合250 km/h及以上车速，高干扰谱适合250 km/h以下车速.

2.2 轨道高低不平顺时域样本的模拟合成

目前国内外对于轨道不平顺时域样本的模拟合成，主要采用的方法有二次滤波法、三角级数法、白噪声滤波法、以及基于功率谱密度采样的轨道不平顺数值模拟新方法等[23].本文采用对轨道线路拟合程度高且能够真实反映线路实际情况的基于功率谱密度采样的轨道不平顺数值模拟新方法对轨道高低不平顺时域样本进行合成，其中，所合成的车辆运行速度为300 km/h时的轨道高低不平顺时域模拟序列如图2所示.

图2 轨道高低不平顺时域模拟序列

3 转向架悬挂系统阻尼比协同优化

为使高铁转向架垂向悬挂系统的阻尼匹配达到最佳，本文利用MATLAB/Simulink和多岛遗传算法，通过构建阻尼比协同优化设计Simulink仿真模型，以人体振动舒适性最佳为目标，以轨道高低不平顺作为输入激励，以一系及二系悬挂垂向行程和一系悬挂垂向动作用力为约束条件，对高铁转向架一系及二系垂向悬挂系统阻尼比进行协同优化.

3.1 舒适性评价指标

为了对高铁一系和二系垂向悬挂系统的阻尼比进行优化设计，首先必须明确人体振动舒适性评价指标.目前，国内外最常用的人体舒适性和健康评价指标为ISO2631标准[24]中提出的加权加速度均方根值，该标准认为人体对不同频率及不同方向振动的敏感程度不同，由于本研究主要针对垂向振动对舒适性的影响进行评价，因此，仅计算垂向振动加权加速度均方根值.其中，在不同频率下的振动频率加权加速度均方根值的频率加权值w(f)的计算公式为

(3)

3.2 阻尼比协同优化设计目标函数

根据每台转向架单侧一系垂向减振器的等效阻尼系数C1、二系垂向减振器的阻尼系数C2，分别与各系悬挂系统参数及待优化设计阻尼比之间的关系，可得

(4)

(5)

式中，ξ1为一系垂向悬挂系统阻尼比，ξ2为二系垂向悬挂系统阻尼比.

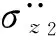
(6)

3.3 阻尼比协同优化设计约束条件

为了保证高铁高速行驶时具有良好的运行平稳性和安全性，在对其转向架垂向悬挂系统阻尼比进行优化设计时，应满足以下约束条件：

(1)一系及二系悬挂垂向行程

为了减小车辆高速行驶过程中撞击限位的概率，使车辆具有良好的运行平稳性和安全性，因此，一系及二系悬挂的垂向行程不应超出其垂向限位行程，即

(7)

(8)

式中，z1-zv为一系悬挂垂向行程，z2-z1为二系悬挂垂向行程，[fd1]为一系悬挂垂向限位行程，[fd2]为二系悬挂垂向限位行程.

(2)一系悬挂垂向动作用力

为了使车轮不抬离轨道表面，以保障车辆的运行安全性，轮对所受的一系悬挂垂向动作用力不应超出其静作用力，即

(9)

3.4 阻尼比协同优化

(1)阻尼比优化设计仿真模型

根据所建立的振动微分方程式(1)及式(4)、(5)，利用MATLAB软件的Simulink工具箱，构建高铁转向架垂向悬挂系统阻尼比协同优化设计Simulink仿真模型，如图3所示.

图3 高铁转向架垂向悬挂系统阻尼比协同优化设计Simulink仿真模型

(2)一系及二系垂向悬挂系统阻尼比优化设计

多岛遗传算法作为一种伪并行遗传算法可有效避免早熟和加快收敛速度，可以很好地在优化域中寻找全局最优解，为此，本文采用多岛遗传算法，利用MATLAB对高铁转向架一系和二系垂向悬挂系统阻尼比进行协同优化，优化设计流程图如图4所示，其中，参数设定如下：高铁一系及二系垂向悬挂系统阻尼比的优化设计初始值ξ1=0、ξ2=0，优化范围ξ1∈(0,0.5)、ξ2∈(0,0.5)；多岛遗传算法的子群规模为10，岛个数为10，进化代数为10，交叉概率为1，变异概率为0.01，迁移概率为0.01，迁移的间隔代数为5.

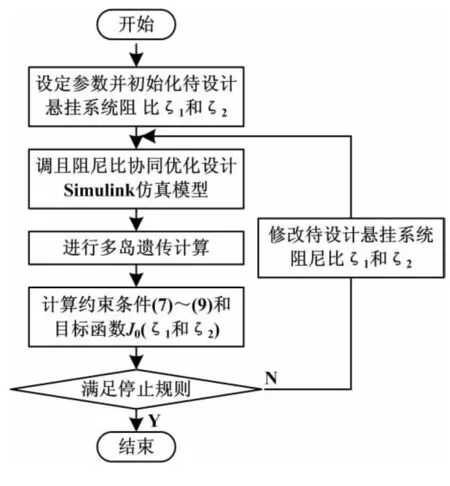
图4 优化设计流程图

根据车辆参数，所建立的Simulink仿真模型及式(6)～(9)，以一系垂向悬挂系统阻尼比ξ1和二系垂向悬挂系统阻尼比ξ2为设计变量，以德国轨道高低不平顺作为轨道输入激励，依据上述

优化设计流程，利用所编写的优化设计程序求目标函数Jo(ξ1,ξ2)的最小值，便可得到高铁一系和二系垂向悬挂系统的最优阻尼比ξ1、ξ2.

4 设计实例

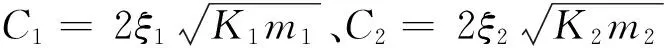
5 仿真验证

在相同车辆结构参数和轨道激励下，分别对转向架垂向悬挂系统阻尼比优化设计前、后的该车辆1/4车体进行了模型仿真，其中，仿真所得到的该车辆优化设计前、后车体垂向振动加速度的时域信号及功率谱密度对比曲线，分别如图5、图6所示.

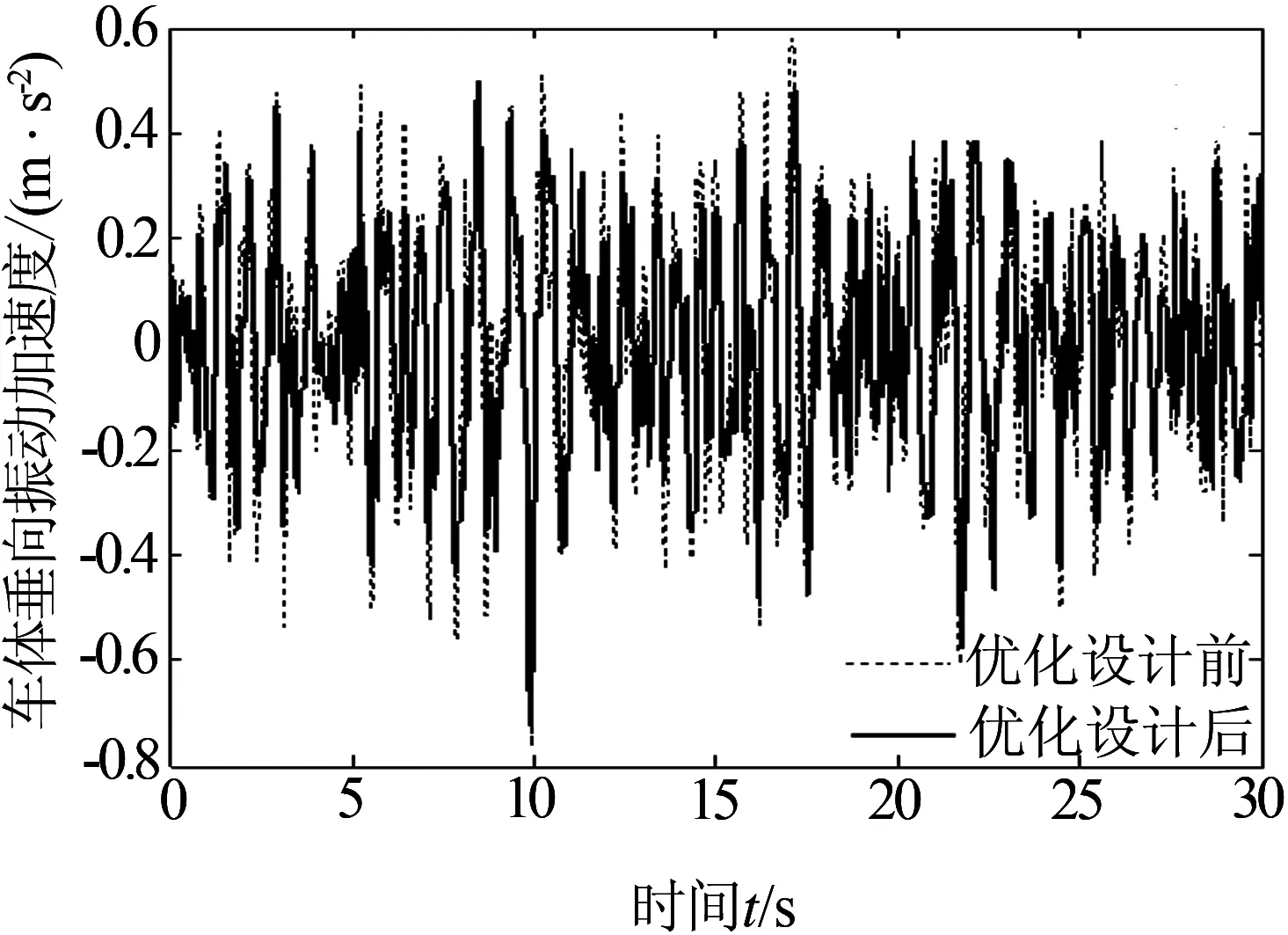
图5 车体垂向振动加速度时域信号

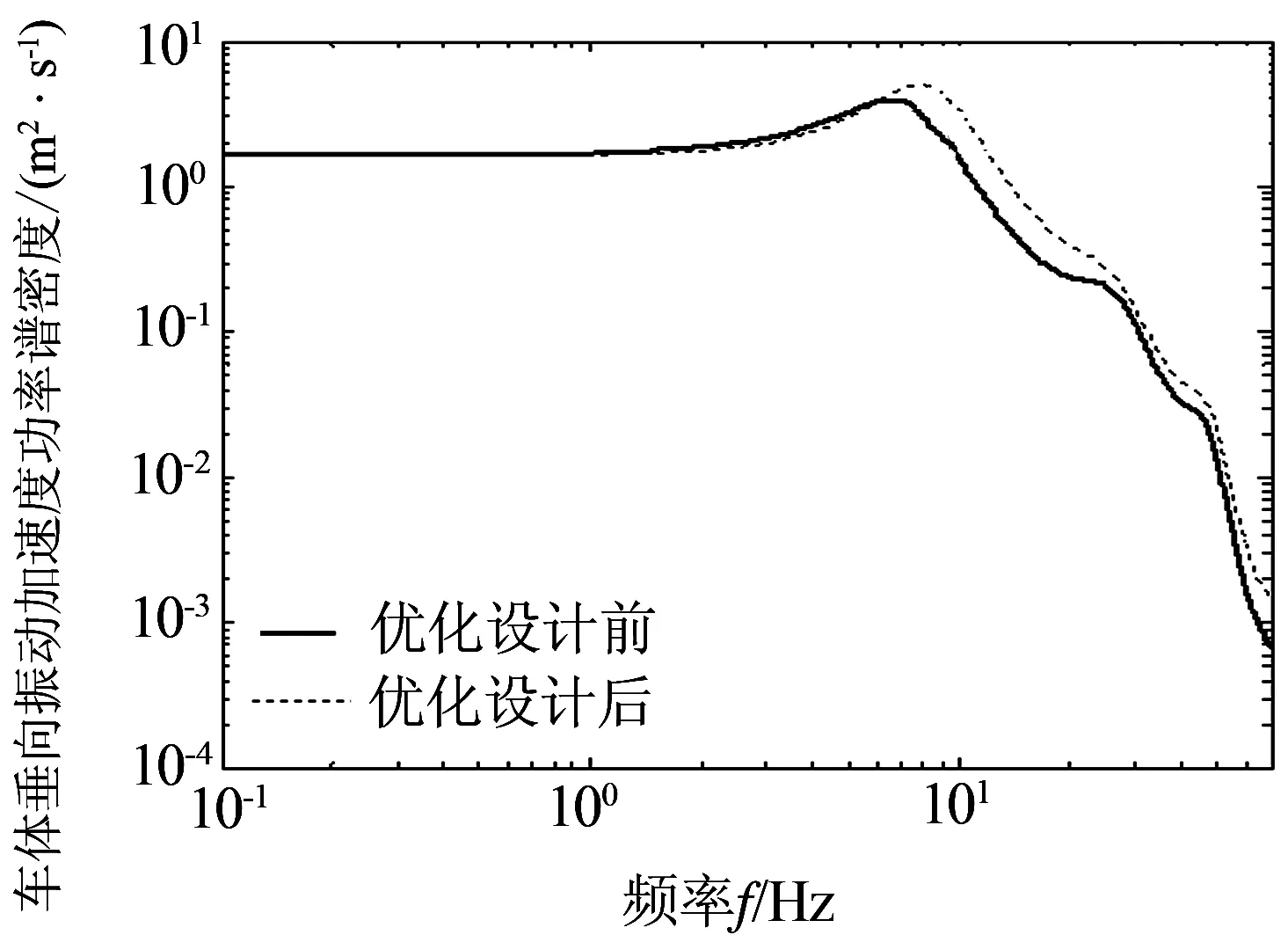
图6 车体垂向振动加速度功率谱密度曲线

分析图5和图6可知，高铁一系和二系垂向悬挂系统阻尼比优化设计后，其车体垂向振动加速度和功率谱密度值比优化设计前有所降低.其中，优化设计前的车体垂向振动加权加速度均方根值为0.24 m/s2，优化设计后的为0.19 m/s2，舒适性提高了20.8%.对比可知，优化设计后车辆的乘坐舒适性得到了明显的提高，表明所设计的一系和二系垂向悬挂系统的最优阻尼比值是可靠的.

6 结论

通过高铁转向架垂向悬挂系统阻尼比协同优化方法的理论研究、实例设计及仿真验证，可知：

(1)根据1/4车体4自由度垂向振动模型，利用MATLAB/Simulink，可建立高铁转向架垂向悬挂系统阻尼比协同优化设计仿真模型;

(2)利用高铁转向架垂向悬挂系统阻尼比协同优化设计仿真模型，以人体振动舒适性最佳为目标，以轨道高低不平顺作为输入激励，以一系及二系悬挂垂向行程和一系悬挂垂向动作用力为约束条件，可建立转向架垂向悬挂系统阻尼比协同优化设计方法;

(3)实例设计及对比验证结果表明：所建立的高铁转向架垂向悬挂系统阻尼比协同优化设计方法是可行的，能够改善高铁的乘坐舒适性，该研究为高铁一系和二系垂向悬挂系统阻尼比的初始设计提供了重要的理论指导，为基于1/4车辆模型的高铁转向架垂向悬挂系统阻尼比的优化设计提供了一种行之有效的指导方法.

[1]王福天．车辆系统动力学[M]．北京：中国铁道出版社，1994．

[2]AUCIELLO J, MELI E, FALOMI S, et al. Dynamic behaviour of tramways with different kinds of bogies[J]. Veh Syst Dyn, 2009, 47(7): 867-899.

[3]孟宏，翟婉明，王开云．二系悬挂对机车动力学性能的影响[J]．铁道机车车辆，2005，25(5)：1-4．

[4]杨国桢，王福天．机车车辆液压减振器[M]．北京：中国铁道出版社，2002．

[5]VERROS G, GOUDAS H, NATSIAVAS S. Dynamics of large scale vehicle models using ADAMS/FLEX[C]. International ADAMS User Conference, 2000.

[6]EOM B G, LEE H S. Assessment of running safety of railway vehicles using multibody dynamics[J]. Int. J. Precis. Eng. Man, 2010, 11(2): 315-320.

[7]EICHBERGER A, HOFMANN G. TMPT: multi-body package SIMPACK[J]. Veh Syst Dyn, 2007, 45(Suppl): 207-216.

[8]WALLRAPP O. Review of past developments in multi-body system dynamics at DLR-from FADYNA to SIMPACK[J]. Veh Syst Dyn, 2004, 41(5): 339-348.

[9]SUGAHARA Y, TAKIGAMI T, KAZATO A. Suppression vertical vibration in railway vehicles through air spring damping control[J]. Journal of System Design and Dynamics, 2007, 1(2): 213-223.

[10]SUGAHARA Y, TAKIGAMI T, KAZATO A, et al. Suppression vertical vibration in railway vehicles by damping force control of primary suspension using an LQG controller[J]. Journal of System Design and Dynamics, 2008, 2(1): 251-262.

[11]NGUYEN H C, SONE A, IBA D, et al. Design of Passive Suspension System of Railway Vehicles via Control Theory[J]. Journal of System Design and Dynamics, 2008, 2(2): 518-527.

[12]ZUO L, NAYFEH S A. Design of Passive Mechanical Systems via Decentralized Control Techniques[C]. 43rd AIAA/ASME/ ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, 2002, AIAA2002-1282: 1-9.

[13]MEI T X, GOODALL R M. Use of multiobjective genetic algorithms to optimize inter-vehicle active suspensions[J]. Journal of Rail and Rapid Transit , 2002, 216(1): 53-63.

[14]MASTINU R M, GOBBI M. On the optimal design of railway passenger vehicles[J]. Journal of Rail and Rapid Transit, 2001, 215: 111-124.

[15]KIM Y G, PARK C K, PARK T W. Design optimization for suspension system of high speed train using neural network[J]. JSME International Journal Series C, 2003, 46(2): 727-735.

[16]KUZNETSOV A, MAMMADOV M, SULTAN I, et al. Optimization of a quarter-car suspension model coupled with the driver biomechanical effects[J]. Journal of Sound and Vibration, 2011, 330(12): 2937-2946.

[17]BATOU A, SOIZE C, CHOI C K, et al. Robust design in multibody dynamics-application to vehicle ride-comfort optimization[J]. Procedia IUTAM, 2015, 13: 90-97.

[18]GEORGIOU G, VERROS G, NATSIAVAS S. Multi-objective optimization of quarter-car models with a passive or semi-active suspension System[J]. Veh Syst Dyn, 2007, 45 (1): 77-92.

[19]郝建华，曾京，邬平波．铁道客车垂向随机减振及悬挂参数优化[J]．铁道学报，2006，28(6)：35-40．

[20]SUGAHARA Y, KAZATO A, TAKIGAMI T, et al. Suppression of vertical vibration in railway vehicles by controlling the damping force of primary and secondary suspensions[J]. QR of RTRI, 2008, 49(1): 7-15.

[21]ZHANG Y W, ZHAO Y, ZHANG Y H, et al. Riding comfort optimization of railway trains based on pseudo-excitation method and symplectic method[J]. Journal of Sound and Vibration, 2013, 332(21): 5255-5270.

[22]NISHIMURA K, PERKINS N C, ZHANG W M. Suspension dynamics and design optimization of a high speed railway vehicle[C]. In Proceedings of the 2004 ASME/IEEE Joint Rail Conference, Maryland, USA, 2004.

[23]翟婉明．车辆-轨道耦合动力学[M]．4版,北京：科学出版社，2015．

[24]ISO 2631-1 . Mechanical Vibration and Shock-Evaluation of Human Exposure to Whole-driver Vibration-Part1: General Requirements, International Organization for Standardization[P].Geneva [s.n.], 1997.

Collaborative Optimization of Bogie Vertical Suspension Damping Ratio for High-Speed Rail

ZHOU Changcheng1, YU Yuewei1, ZHAO Leilei1,2

(1. School of Transportation and Vehicle Engineering, Shandong University of Technology, Zibo 255049, China; 2. School of Automation, Beijing University of Posts and Telecommunications, Beijing 100876, China)

According to the 1/4 vehicle body four-degree-of-freedom vertical vibration model of high-speed rail, a collaborative optimal design simulation model for damping ratio of bogie vertical suspension was established using MATLAB/Simulink. Taking optimal ride comfort as target, a collaborative optimal design mathematical model for damping ratio of bogie vertical suspension was built. Using track vertical profile irregularity as input and using the primary and secondary suspension vertical stroke and the vertical dynamic force of primary suspension as constraint conditions, a collaborative optimization design method for damping ratio of the bogie vertical suspension was presented. With a practical example of high-speed rail, the damping ratio was designed. The results show that the damping ratio value designed can significantly improve ride comfort. Thus, the collaborative optimization method of bogie vertical suspension damping ratio for high-speed rail is correct. This research provides important theoretical basis for the initial design of the damping ratio of the primary and secondary vertical suspension system of high-speed rail.

high-speed rail; bogie vertical suspension; damping ratio; collaborative optimization

1673-9590(2016)04-0055-06

2015-12-14

国家自然科学基金资助项目(51575325)；山东省自然科学基金资助项目(ZR2013EEM007)；山东省重点研发计划资助项目(2015GGX105006)

周长城(1962-)，男，教授，博士，主要从事汽车和轨道车辆悬架设计及理论的研究E-mail:greatwall@sdut.edu.cn.

A