非高斯噪声下的信号检测算法与性能分析

刘 进

(中国电子科技集团公司第20研究所，西安 710068)



非高斯噪声下的信号检测算法与性能分析

刘 进

(中国电子科技集团公司第20研究所，西安 710068)

为改善非高斯背景噪声下的信号检测性能，提出了采用非线性阈值系统的信号检测算法。该算法首先利用阈值系统对接收信号进行预处理，其次采用最小平均错误概率准则对预处理后的信号进行检测，最后推导了所提检测算法的误码率解析表达式并给出仿真验证。理论分析和仿真结果表明：在高斯背景噪声下，线性最佳检测算法的检测性能优于所提检测算法；在非高斯背景噪声下，所提检测算法的检测性能较线性最佳检测算法有显著提升。

信号检测；非高斯背景噪声；非线性阈值系统；线性最佳检测算法

0 引 言

在无线通信系统中，噪声作为危害信息可靠传输的因素会对信号的接收产生严重影响[1]。信号波形检测的任务就是根据检测性能需求，设计与环境相匹配的检测系统，从被噪声污染的接收信号中有效地提取有用信号[2]。信号检测系统通常是在一定的假设条件下，满足某种“最佳”准则的“最佳”检测系统。其中，最小平均错误概率准则是最经常采用的“最佳”准则[2]。现有的信号检测算法中,信道噪声通常都假设为高斯噪声[3]，此时采用线性检测算法可以得到闭式解。在非高斯背景噪声下，通常需要采用非线性的信号检测算法，导致检测算法的理论分析非常复杂。

尽管如此，实际应用场景中的噪声如大气噪声[4]、水下噪声[5]、图像噪声[6-7]等通常具有非稳态的特性，属于非高斯噪声的范畴。这类噪声不再服从高斯分布，其共同特点是具有突发性和冲击性，需要用具有更长概率密度函数拖尾的分布来描述。作为一种典型的非高斯噪声，广义高斯噪声已经普遍应用于实际场景中的非高斯噪声建模[8]。目前，广义高斯噪声下的信号检测成为国内外学者关注和研究的热点[9-10]。

在高斯信道噪声条件下，采用最小平均错误概率准则的线性检测算法性能最优且理论分析简单。在广义高斯噪声条件下，线性最佳检测算法的性能不再是最优的，这就为改善信号的检测性能提供了可能；同时，广义高斯噪声相关时间的有色性和概率密度的非高斯性使得信号检测理论分析变得困难。本文针对广义高斯背景噪声下的信号检测问题，提出采用非线性阈值系统的信号波形检测算法，算法理论分析简单且检测性能优于线性最佳检测算法。

1 线性最佳检测算法

假设传输的信号为二进制数字基带信号，在H0假设下，发送信息 “0”时信号波形为s0(t)；在H1假设下，发送信息“1”时信号波形为s1(t)。存在噪声干扰时接收信号是噪声和发送信号的混合波形，可以表示为：

(1)

当发送信号波形为s0(t)和s1(t)时，接收信号r(t)的k维概率密度函数表示为[2]：

(2)

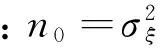
(3)

当发送信号s0(t)和s1(t)先验等概率(P0=P1)时，将式(2)代入式(3)并化简后得到：

(4)

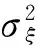
(5)

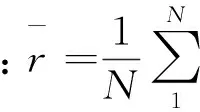
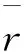
由信号检测的基本理论可知，在高斯背景噪声的条件下，采用最小平均错误概率准则的线性最佳检测算法的误码率是理论上可能达到的最小值，其误码率表示为[2]：

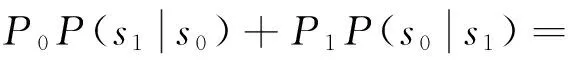
(6)

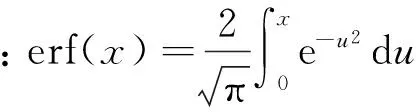
2 采用非线性阈值系统(NTS)的信号检测算法

2.1 检测算法模型

为改善非高斯背景噪声下的信号检测性能，引入非线性阈值系统(NTS)，构建了采用NTS的非线性检测系统，模型如图1所示。原理是首先对接收信号进行采样，其次利用NTS对离散采样信号进行非线性阈值预处理，最后采用最小平均错误概率准则对预处理后的信号进行检测。

图1 采用NTS的检测算法模型

假设传输的二进制离散信号为s0(k)=0和s1(k)=1，1≤k≤N，N为每个码元持续时间内的采样点数。则接收信号可以表示为：

(7)

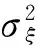
(8)

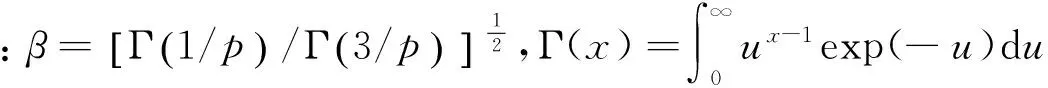
式(8)的噪声概率密度函数能够表示多种常用的噪声。当p=1时，噪声为拉普拉斯噪声；当p=2时为高斯噪声；当p→∞时为均匀分布的噪声。广义高斯噪声分布(p<2)的概率密度函数拖尾的下降率低于高斯型噪声分布，具有一定的突发性和冲击性，更适合于描述实际应用场景中非稳态的噪声分布。

2.2 检测算法误码率性能分析

在图1所示的基于NTS的检测算法中，当接收信号采样值大于阈值θ时，系统输出为b，反之系统输出为a。为方便分析，假设阈值节点为符号函数，即a=-1,b=1，此时NTS的输出信号表示为：

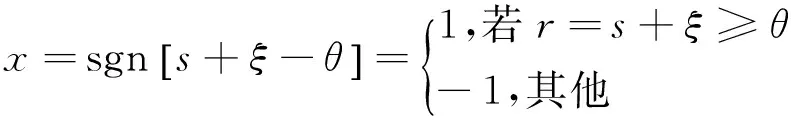
(9)

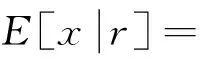
θ)-P(s+ξ<θ)=1-2Fξ(θ-s)

(10)

同时可以计算得到：

(11)

由式(10)和(11)可以计算出NTS输出信号x的方差为：

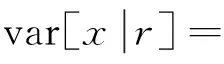
(12)

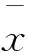
(13)

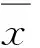
(14)

对经过NTS预处理后的信号采用最小平均错误概率准则进行检测，其判决式表示为：

(15)

将式(14)代入式(15)并取对数，在发送s0和s1先验等概(P0=P1)的条件下，上式简化为：

(16)

对式(16)进行变换后得到：

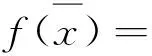
(17)

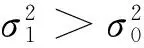
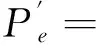
(18)

(19)

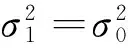
(20)

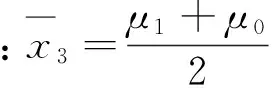
3 仿真结果及分析

3.1 相关系数计算

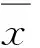
(21)

式中：i=0或1。

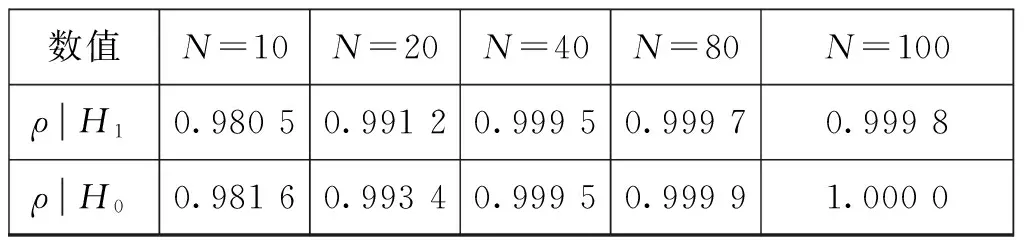
表1 相关系数计算值

3.2 检测性能仿真与分析

图2给出了高斯背景噪声(式(8)中p=2)下的检测性能曲线，噪声均方值σξ取1～10，采样点数N=20，线性最佳检测算法的性能优于本文所提检测算法的性能，仿真结果与理论值相吻合。图3给出了拉普拉斯型背景噪声(p=1)下的检测性能曲线，噪声均方值σξ取值1～10，采样点数N=20，所提检测算法性能优于线性最佳检测算法，仿真结果与理论值相吻合。由此得到以下结论：(1)在高斯背景噪声条件下，线性最佳检测算法的性能优于本文所提算法。(2)在非高斯背景噪声条件下，线性最优检测算法的前提条件(高斯背景噪声假设)不再成立，所提检测算法的性能优于线性最佳检测算法。

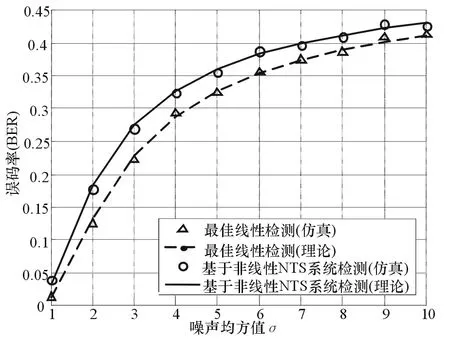
图2 高斯噪声条件下的检测性能曲线

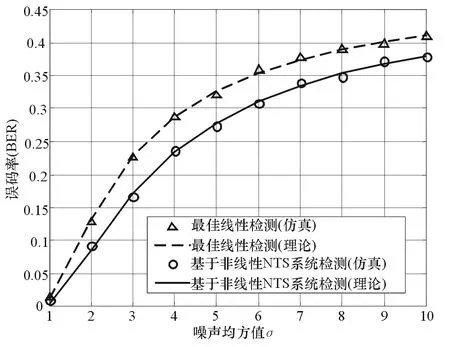
图3 拉普拉斯噪声条件下的检测性能曲线

4 结束语

提出了一种采用非线性阈值系统的信号检测算法，以改善非高斯背景噪声下的信号检测性能。该算法采用简单的非线性阈值系统对接收信号进行处理，克服了传统非线性检测算法理论分析和实现复杂的缺点。在典型的非高斯噪声(广义高斯背景噪声)条件下，理论推导和仿真结果相吻合，且均表明所提检测算法性能较线性最佳检测算法有显著提升。本文只是非线性阈值信号处理技术在非高斯背景噪声下信号检测的初步探索，进一步的深入研究可以考虑将多阈值系统信号技术处理推广到多元假设的信号检测中。

[1] MOLISCH A F.Wireless communications[M].England:Cambridge University,2011.

[2] 赵树杰,赵建.信号检测与估计理论[M].北京:清华大学出版社,2005.

[3] 齐佩汉,司江勃,李赞.新型抗噪声不确定度谱分段对消频谱感知算法[J].西安电子科技大学学报,2013,40(6):19-24.

[4] SHEPELAVEY B.Non-Gaussian atmospheric noise in binary-data,phase-coherent communication systems[J].IEEE Transactions on Communications Systems,1963,11(3):280-284.

[5] BANERJEE S,AGRAWAL M.Underwater acoustic noise with generalized Gaussian statistics:Effects on error performance[C]//2013 MTS/IEEE on OCEANS,2013:1-8.

[6] CHARTRAND R,STANEVA V.Total variation regularisation of images corrupted by non-Gaussian noise using a quasi-Newton method [J].IET Image Processing,2008,2(6):295-303.

[7] CHAINAIS P.Towards dictionary learning from images with non Gaussian noise[C]//2012 IEEE International Workshop on Machine Learning for Signal Processing (MLSP),2012:1-6.

[8] MILLER J H.Detectors for discrete-time signals in non-Gaussian noise[J].IEEE Transactions on Information Theory,1972,18(2): 241-250.

[9] SOURY H,YILMAZ F,ALOUINI M S.Average bit error probability of binary coherent signaling over generalized fading channels subject to additive generalized gaussian noise[J].IEEE Communications Letters,2012,16 (6):785-788.

[10]SOURY H,YILMAZ F,ALOUINI M S.Error rates of M-PAM and M-QAM in generalized fading and generalized gaussian noise environments [J].IEEE Communications Letters,2013,17(10):1932-1935.

Signal Detection Algorithm and Performance Analysis under Non-Gaussian Noise

LIU Jin

(The 20th Research Institute of CSIC,Xi'an 710068，China)

To improve the signal detection performance under non-Gaussian background noise,this paper presents a novel signal detection algorithm based on nonlinear threshold system (NTS).The algorithm firstly uses NTS to preprocess the received signal,then uses the minimum mean error probability rule to detect the preprocessed signals,finally deduces the analytical expression of the bit error ratio (BER) of proposed detection algorithm and gives the simulative validation.Theoretical analysis and simulation results show:under the background of Gaussian noise,the detection performance of the linear optimal detection algorithm is better than that of the proposed detection algorithm;under the background of non-Gaussian noise,the detection performance of proposed algorithm is significantly improved compared with that of linear optimal detection algorithm.

signal detection;non-Gaussian background noise;nonlinear threshold system;linear optimal detection algorithm.

2016-04-05

TN911.7

A

CN32-1413(2016)04-0068-05

10.16426/j.cnki.jcdzdk.2016.04.016