大气湍流及瞄准误差对激光通信误码率影响研究

任建迎，孙华燕，张来线

(中国人民解放军装备学院 a.研究生院; b.光电装备系，北京 101416)



【基础理论与应用研究】

大气湍流及瞄准误差对激光通信误码率影响研究

任建迎a，孙华燕b，张来线b

(中国人民解放军装备学院 a.研究生院; b.光电装备系，北京 101416)

以Gamma-Gamma大气湍流信道和探测器信号两个模型为基础，采用直接检测(IM/DD)开关键控(OOK)强度调制方式，推导出了自由空间光系统误码率闭合表达式，分析了大气湍流、归一化光束宽度、归一化瞄准误差等对系统性能的影响；对系统误码率闭合表达式进行了数值模拟分析，结果表明在固定发射功率下通过优化发射光束宽度、减小瞄准误差可以使系统性能达到最优。

大气湍流；瞄准误差；光束宽度；激光通信；误码率

在近地面几公里范围内，自由空间光(FSO)通信链路的应用越来越广泛，相比于射频链路，FSO链路不仅对周围环境干扰小、安全不易被探测，而且FSO链路设备轻便、成本低、易于部署。但是在近地FSO通信链路中，由大气温度不均匀引起折射率的随机变化，压强的波动引起光强闪烁，这对FSO通信链路的误码率有很大的影响。通过大量的研究分析表明：Gamma-Gamma分布是比较符合强湍流条件下的大气信道模型[1-2]。通信链路除受闪烁影响外，接收信号还受到设备抖动等引起的瞄准误差的影响[3]，当发射和接收设备位于运动载体时抖动误差尤其严重。相对于波束宽度接收口径造成的误差可以忽略不计，但由湍流和瞄准误差引起的误码性能值得研究。文献[4]也对湍流和瞄准误差进行了分析,文献[9]推导出了开关键控在K分布衰减和瞄准损失下的ASEP(平均误码率)计算公式，并提出了瞄准误差的优化模型,上述方式计算量比较大，没有给出闭合解。本文针对大气湍流强度起伏模型和瞄准误差损失模型进行了分析推导，采用强湍流下的Gamma-Gamma分布模型和瞄准误差的瑞利分布模型，利用级数求和的方法得到ASEP公式，并对不同湍流尺度、不同瞄准误差、不同光束宽度下的通信链路的平均误码率进行了数值模拟分析。

1 大气信道统计模型

探测器接收到的信号可表示为[4]

y=hRx+n

(1)

h=hlhahp

(2)

式(2)中hl是与路程相关的损失参数，hp是瞄准误差造成的随机损失，ha是大气湍流造成的光强随机衰减，因为瞄准误差引起的随机抖动的相关时间远远大于湍流引起闪烁的相关时间，所以可认为ha和hp相互独立，其概率分布函数分别为fa(ha)和fp(hp)[3]。

1.1 大气湍流强度起伏模型

Gamma-Gamma分布模型比较符合中强湍流强度起伏的特点[3]，ha的强度起伏的概率密度函数为[4-5]

(3)

其中Κα-β(·)是第二类修正的贝塞尔函数，α，β分别是与Rytov方差相关的参数[9]。文献[4]描述了Gamma-Gamma概率密度函数在变化的湍流中的测试结果。

1.2 瞄准误差损失模型

在FSO通信链路中，由于大气折射率的变化引起光束的随机偏移，造成探测器处的信号衰减和瞄准误差。高斯光束在大气湍流中传播距离z后的宽度，可以近似表示为ωz：

(4)

瞄准误差可近似表示为[4]

(5)

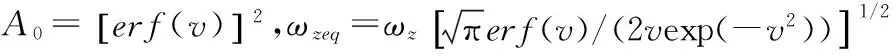
假设水平方向和垂直方向的偏移量相同，采用Rayleigh分布的光束偏移模型：

(6)

瞄准误差hp的概率分布可表示为[1，6]

(7)

η=ωzeq/2σs，探测器处的等效光束半径和指向位移误差之比。

根据Gamma-Gamma分布衰减模型和瞄准误差衰减模型，由此得到h=hlhahp的概率分布模型[3-5]：

(8)

在中强度湍流区，fha(ha)服从Gamma-Gamma分布，把式(3)代入式(8)，得：

(9)

1.3 大气信道平均误码率模型

强度调制/直接检测的OOK调制方式的误码率计算公式为[1]

(10)

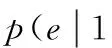
(11)

通过式(11)和概率密度函数h求得平均误码率[2-3]：

(12)

把式(9)和式(11)代入式(12)，经整理得误码率近似解[3]：

(13)

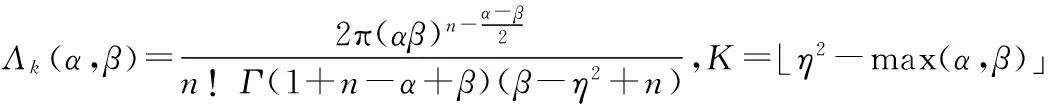
2 数值模拟分析

为了分析各个参数对自由空间光通信系统性能的影响，对以上推导得到的表达式进行仿真分析，FSO系统链路参数参见表1。

表1 FSO链路的主要参数

归一化光束宽度(ωz/Ra=10,8,6)在不同湍流尺度下的平均误码率曲线如图1所示。从图1可以看出，误码率随着Rytov参数增大而减小。当光束变窄时误码率增大，这是由于在光束偏离量一定的情况下，光束越窄，受抖动影响越大，中断概率越大，导致误码率升高[1]。而由先验知识可知当功率一定时，光束宽度增大，探测器所接收的信号功率变小，判决错误概率就会增加[7]。因此，要选择合适的发射光束宽度，使抖动和接收功率影响下的误码率降到最低。

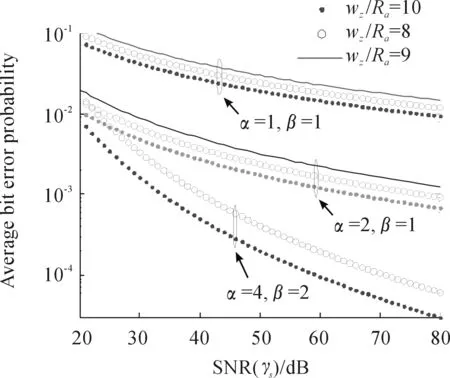
图1 当σs/Ra=3时，不同α、β参数和光束宽度下的平均误码率随信噪比变化曲线

当链路参数不变，光束偏移量、发射光束宽度一定时，由本文第二节内容可知此时误码率主要受大气信道湍流的影响。图2给出了归一化光束偏移量为σs/Ra=3和归一化光束宽度为ωz/Ra=10时，不同α、β值下的平均误码率；即不同Rytov 参数下误码率。由文献[9]，Rytov方差与α、β的值成反比关系。从仿真结果可得，误码率随着α、β的增大而减小，即误码率随着湍流强度的增大而增加。此时的系统性能恶化，可以通过增加发射功率减小系统误码率。

图2 当σs/Ra=3,ωz/Ra=10时，不同α、β参数的平均误码率随信噪比变化曲线

在系统链路参数固定，大气湍流环境稳定的情况下，考虑机械抖动的影响十分必要，其他参数固定，机械抖动的影响主要表现在接收端光束偏移量。图3给出了当Rytov参数一定时即α=2,β=1，归一化光束宽度一定为ωz/Ra=10时，光束的归一化偏移量分别为σs/Ra=10,5,3,1不同值时的误码率曲线。由图3可得当归一化偏移量逐渐变大，误码率升高。

图3 当α=2,β=1,ωz/Ra=10时，不同瞄准误差下误码率随信噪比变化曲线

以上仿真在没有考虑接收光学增益，所以仿真结果显示的所需信噪比比较高。根据对30 cm口径接收光学系统的实验测试可知，光学增益可达20 dB。综合考虑湍流强弱、瞄准误差、光束宽度等影响因素，只有瞄准误差和发射光束宽度可控，且瞄准误差仅能减小不可能消除，因此在一定机械瞄准精度下为提高链路通信可靠性，最优方法就是通过适当增加发射功率和发射光束宽度来平衡指向误差带来的误码率。对于给定发射功率和误码率要求的链路，可以通过选择最优波束宽度满足误码率低的要求。优化问题需要特殊算法且推导过程十分复杂，本文在此不做说明。

3 结论

通过建立大气湍流影响和瞄准误差影响的信道模型并结合数值模拟结果分析，可以得出以下结论：

1) 机械抖动和大气折射共同作用使光束偏移量增大，系统的中断概率增加，误码率上升。增加发射光束宽度是减小光束抖动引起系统中断的有效手段，但增加光束宽度造成接收光功率的下降，增加了阈值判决的误码率，因此合理选择最优化光束宽度是降低系统误码率的重要课题内容之一。

2) 与Rytov方差相关的参数α、β是影响误码率的重要因素，误码率随着α、β的增大而减小，而Rytov方差是与湍流强度相关的，所以在同一湍流强度下，适当增加光束宽度可以一定程度减小瞄准误差，从而降低误码率。

本文建立的大气信道误码率计算模型对FSO通信链路的工程应用提供了一定的理论分析和性能评估依据，但由于大气信道的不确定性，信道模型与实际信道有一定的差异，特别是最优化光束宽度需要进一步研究。

[1] BAYAKI E,SCHOBER R,MAILLIK R K.Performance Analysis of MIMO Free-Space Optical Systems in Gamma-Gamma Fading[J].IEEE,2009(12):3415-3424.

[2] UYSAL M,JLI,YU M.Error Rate Performance Analysis of Coded free-Space Optical Links Over Gamma-Gamma Atmospheric Turbulence Channels[J].IEEE,2003,5(6):1229-1223.

[3] HARILAOS G,SANDALIDIS,THEODOROS A,et al.BER Performance of FSO Links over Strong Atmospheric Turbulence Channels with Pointing Errors[J].IEEE,2008:44-46.

[4] PRABUKRISHNAN,SRIRAMKUMAR D.Bit Error Rate Analysis of Free-Space Optical System with Spatial Diversity over Strog Atmospheric Turbulence Channel with Pointing Errors[C]//SPIE,2014,126108：1-7.

[5] GAPPMAIR W,HRANILOVIC S,LEITGEB E.OOK Performance for Terrestrial FSO Links in Turbulent Atmosphere with Pointing Errors Modeled by Hoyt Distributions[C]//IEEE,2011,7798:875-877.

[6] FARID A A,HRANILOVIC S.Outage Cpacity Optimization for Free-Space Optical Links With Pointing Errors[C].2007,8724:1702-1710.

[7] GAPPMAIR W,HRANILOVIC S,LEITGEB E.Performanceof PPM on Terrestrial FSO Links with Turbulence and Pointing Errors[J].IEEE,2010,14(5):468-470.

[8] 韩立强，王祁，信太克归.Gamma-Gamma大气湍流下自由空间光通信的性能[J].红外与激光工程，2011,40(7)：1318-1323.[9] 韩立强，游雅晖.大气湍流及瞄准误差联合效应下自由空间光通信的性能[J].光学学报，2014,34(11)：1106005.

[10]王玲，冯莹.信号光束宽度对不同漂移误差的空间光通信系统误码率影响的研究[J].光学与光电技术，2010,8(4)：26-30.

[11]LIU X.Free-space Optics Optimization Models for Building Sway and Atmospheric Interference Using Variable Wavelength[C].IEEE,2009,2:492-493.

[12]王江安，赵英俊，陈冬，等.湍流尺度对大气激光通信系统误码率的影响[J].红外与激光工程，2009,38(4)：655-659.

(责任编辑 周江川)

Bit Error Rate Analysis of Laser Communication over Atmospheric Turbulence Channel with Pointing Errors

REN Jian-yinga, SUN Hua-yanb, ZHANG Lai-xianb

(a.Company of Postgraduate Management; b.Deparment of Photoelectric Equipment, EquipementAcademy of PLA, Beijing 101416, China)

Based on both Gamma-Gamma atmospheric turbulence channel and photoelectric detection signal model, the FSO system used intensity-modulation/direct detection(IM/DD) with on-off key (OOK) and the novel closed-form expressions of bit error rate(BER) for FSO system was derived. How the performance is affected by the atmospheric turbulence and other parameters such as the normalized beamwidth, the normalized jitter was researched. Numerical simulation was further provided to verify the derived analytical expressions. The results show that optimizing the beamwidth and reducing the point error can achieve the minimum BER for a given average transmitted optical power.

atmospheric turbulence; pointing error; beam width; laser link; BER

2016-05-17；

2016-06-18

任建迎(1988—)，男，硕士研究生，主要从事光电信息处理与对抗研究。

10.11809/scbgxb2016.10.040

任建迎，孙华燕，张来线.大气湍流及瞄准误差对激光通信误码率影响研究[J].兵器装备工程学报，2016(10):190-193.

format:REN Jian-ying, SUN Hua-yan, ZHANG Lai-xian.Bit Error Rate Analysis of Laser Communication over Atmospheric Turbulence Channel with Pointing Errors[J].Journal of Ordnance Equipment Engineering,2016(10):190-193.

TN249

A

2096-2304(2016)10-0190-04