基于RANS方法超空泡流数值计算方法研究

杜佩佩，肖昌润，张 露，郑文龙，焦玉超

(海军工程大学 舰船工程系，武汉 430033)



【基础理论与应用研究】

基于RANS方法超空泡流数值计算方法研究

杜佩佩，肖昌润，张 露，郑文龙，焦玉超

(海军工程大学 舰船工程系，武汉 430033)

为了得到超空泡流准确的数值计算方法，基于乌克兰国家科学院IHM的空泡形态计算经验公式与Logvinovich空泡截面独立扩张原理，利用数值优化的方法，建立了空泡形态计算模型；采用有限体积法验证了超空泡流的数值离散方法，对不同空化数下，5种两方程RANS模型进行了数值计算，数值计算结果与基于经验公式的空泡验证模型比较表明：Kω-Sst模型相比其他两方程RANS模型准确度更高，关于空泡最大截面直径的无量纲计算误差小于14%；对空泡长度的数值计算误差小于8%，空化数小于0.01时，小于4%。基于建立的准确数值计算模型，对空化数为0.015时超空泡航行体进行了流场特性数值计算。结果表明：由于空化器锐缘影响，在空化器后部形成了高速气流区域并且存在明显的速度梯度，艏部空化器附近承受静水压力达123个大气压。基于数值计算结果，为超空泡航行体设计提供了改进意见。

超空泡；湍流模型；有限体积法；CFD

超空泡技术早期主要通过理论研究，利用试验进行理论修正，得到了很多经典的空泡流知识：如Helmholtz等人的自由流线理论， Levi-Civita[1]和Villat[2]在其基础上进一步的研究，增强了该理论在强烈扰动和高弯曲度绕流问题的适用性；Wu[3]经过一系列分析，提出了一种非线性自由流线理论，可以解决非零空化数的空泡流问题，但是对复杂绕流问题的处理能力，尤其是其尾部封闭区域超空泡流的水动力问题，至今没有得到很好解决。

对于超空泡航行体的CFD模拟，主要是基于RANS方法的两方程涡黏模型和Reynolds代数应力模型(ASM)。涉及到两相、甚至三相以上的多相流问题，自然超空泡的研究主要是应用均相流的Mixture模型，通气超空泡的研究主要使用VOF模型[4]。对于空泡产生过程中水汽质量输运过程，早期主要使用Singhal等人提出的Singhal完全空化模型进行分析，近年来主要应用基于Rayleigh-Plesset方程的Zwart-Gerber-Belamri模型和Schnerr and Sauer模型。

1969年，在Reichardt等人的研究基础上，Logvinovich提出了可以解决非定常轴对称空泡问题的Logvinovich原理(即空泡截面独立膨胀原理)。Serebryakow[5]、Pellone[6]等人对该理论进行了完善，推导出几个适用性更强的空泡截面发展方程，用偏微分方程加入空泡延迟效应研究空泡截面发展。随后Serebryakow等[5]利用细长体理论，分析超空泡航行体跨、超音速运行时的定常流动，建立了一系列空泡发展模型。国内高强等[7]主要在该理论的基础上推导了超空泡的形态发展方程和跨、超音速流动时的微积分方程，开始利用回转体线性源汇的方法，求解超空泡航行体的空泡形态尺寸和流场压力分布情况。

对于流场计算过程，主要通过湍流模型对计算方程进行封闭。文献[8]比较了ASM模型、RNGk-ε模型和标准的k-ε模型结合3种壁面函数处理方法，认为ASM模型和RNGk-ε模型，同时结合增强壁面函数法计算精度较高；文献[9]选用了RNGk-ε模型，认为其可以更好地处理应变率高、流线变化大的流动问题；文献[10]比较了SSTk-ωDES、k-ε模型对航行体非定常运动过程的数值模拟，认为SSTk-ωDES模型精度更高。

由于超空泡流本身的复杂性，超空泡航行体CFD数值模拟方法难度较高。截止目前为止，多通过空泡形态以及数值模拟结果相互比较的方法验证或者选取计算模型，还没有给出定量的数值比较和较为准确的超空泡流场的CFD算法，本文应用基于Rayleigh-Plesset方程的Schnerr and Sauer空化模型，选用Mixture的均相流模型，基于乌克兰国家科学院IHM的空泡形态计算经验公式与Logvinovich空泡截面独立扩张原理建立新的空泡形态计算模型，采用有限体积法，通过对不同空化数下，5种两方程RANS方法湍流模型的空泡长度、径向最大宽度等形态参数数值计算结果与经验公式比较，提出了准确的超空泡航行体CFD数值计算方法。在建立准确数值计算模型基础上，对超空泡流场特性进行了分析，为超空泡航行体设计提出了改进意见，凸显了CFD优势。

1 数值计算方法

1.1 基本数学模型

雷诺平均模型，是将瞬时的Navier-Stokes方程求解变量分解成平均的(时间平均和总体平均)和波动的分量。速度分量为：

(1)

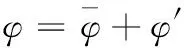
(2)

式中φ可以为压力、能量或者组分浓度。

将以上两公示的表达形式带入瞬时的连续性方程和动量方程，同时取时间平均和总体平均的动量方程，得到了如下的笛卡尔坐标形式的雷诺平均Navier-Stokes方程。

(3)

(4)

本文选择基于Rayleigh-Plesset方程的Schnerr and Sauer空化模型，考虑气泡的生长和溃灭，气液两相输运方程为：

(5)

其对应的蒸发和凝结速率可分别表示为：

(6)

(7)

其中：pc为水的饱和蒸汽压，取3 169 Pa；Cprod、Cdest分别取1、2。

气泡半径R通过下式计算：

(8)

1.2 RANS两方程模型

1) Standardk-ε模型

标准k-ε模型的湍动能k和湍动耗散率ε可以通过以下两式进行计算。

(9)

(10)

(11)

式中，Gk表示平均速度分量产生的湍动能；Gb表示由于浮力作用所产生的湍动能；YM表示可压缩湍动流中由于脉动膨胀所产生的湍动能量耗散；C1ε=1.44、C2ε=1.92、Cμ=0.09σk=1.0、σε=1.3为常数，Sk和Sε为自定义源项。

2) RNGk-εModel

RNGk-ε模型的输运方程与标准k-ε模型相同。湍动黏性满足：

(12)

3) Realizablek-ε模型

Realizablek-ε模型的输运方程为：

(13)

(14)

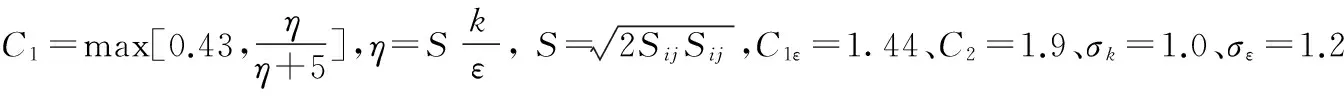
4) Standardk-ω模型

Standardk-ω模型的湍动能k和湍动耗散率ω可以通过下列公示确定。

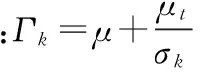
(17)

5)Shear-StressTransport(SST)k-ω模型

SSTk-ω模型的输运方程与Standardk-ω方程相同。湍动黏性通过以下计算。

(18)

其中S是应变率的大小，并且：

1.3 研究对象和计算条件

本文选取文献[5]中给出的无尾翼鱼雷模型(如图1所示)，进行超空泡航行体数值计算方法的研究。主要包括圆盘空化器、尾喷管、锥柱段弹体。主要几何尺寸：空化器直径(Dn)为10 mm，模型总长(Ln)520 mm，最大直径为38 mm，尾喷管直径19 mm。目前在对超空泡航行体CFD模拟，该模型应用广泛、方法成熟、试验技术成熟，许多专家、学者都以此为对象进行超空泡的探索、研究。

基于以上几何模型，利用ICEM软件，建立标准的三维结构化网格，对圆盘空化器入口表面、侧面以及锥段体等进行局部加密。

计算域的进口采用速度入口，通过入口速度的改变实现空化数的调整。出口采用压力出口，远场采用固壁边界条件。使用SIMPLE压力-速度耦合项，采用标准的压力离散格式，其余均采用一阶迎风格式。

图1 几何模型

1.4 数值离散方法

在计算流体流体力学数值仿真过程中，作为前处理的数值离散方法的准确性对数值计算结果准确性至关重要。通常，由于网格之间在数值传递的过程中存在截断误差，而划分网格的类型和网格生成的数量直接决定了误差的大小。理论上，为了提高计算精度，降低误差增加网格密度。但是考虑到计算机的计算开销，在满足误差要求的前提下，尽可能降低网格的密度，突显CFD的优势。

目前主要通过划分结构网格和非结构网格进行数值离散，非结构网格虽然前处理过程简单、易实现，但是计算收敛耗时长，对于精细流场问题的处理准确度低。本文选用结构化网格划分方法，具体划分结果如表1所示。

表1 网格划分结果

图2 160万网格数目时，网格划分结果

2 计算结果及分析

2.1 网格密度对计算结果的影响

计算得到了不同空化数下，航行体形成超空泡的长度和最大截面宽度值。由图3和图4可知，网格密度为114万时，空泡长度低于其他网格密度，空泡的宽度值更加明显。160万网格密度和215万网格在计算空泡长度和空泡最大截面宽度值相差不大，网格密度为280万时，当空化数大于0.02时精度明显更高。因此，考虑到计算机的消耗机时和数值精度，在后续数值计算中选取网格密度为160万，同时限定空化数小于0.02，确保计算精度。

图5给出了空化数为0.01时，超空泡航行体的速度场分布图，在空泡内部蒸汽相的速度为0，而超空泡所产生的尾流影响非常明显，可以延伸很远，所以在做非定常工况数值模拟的过程中，应增加航行体尾流区域计算域的尺寸。

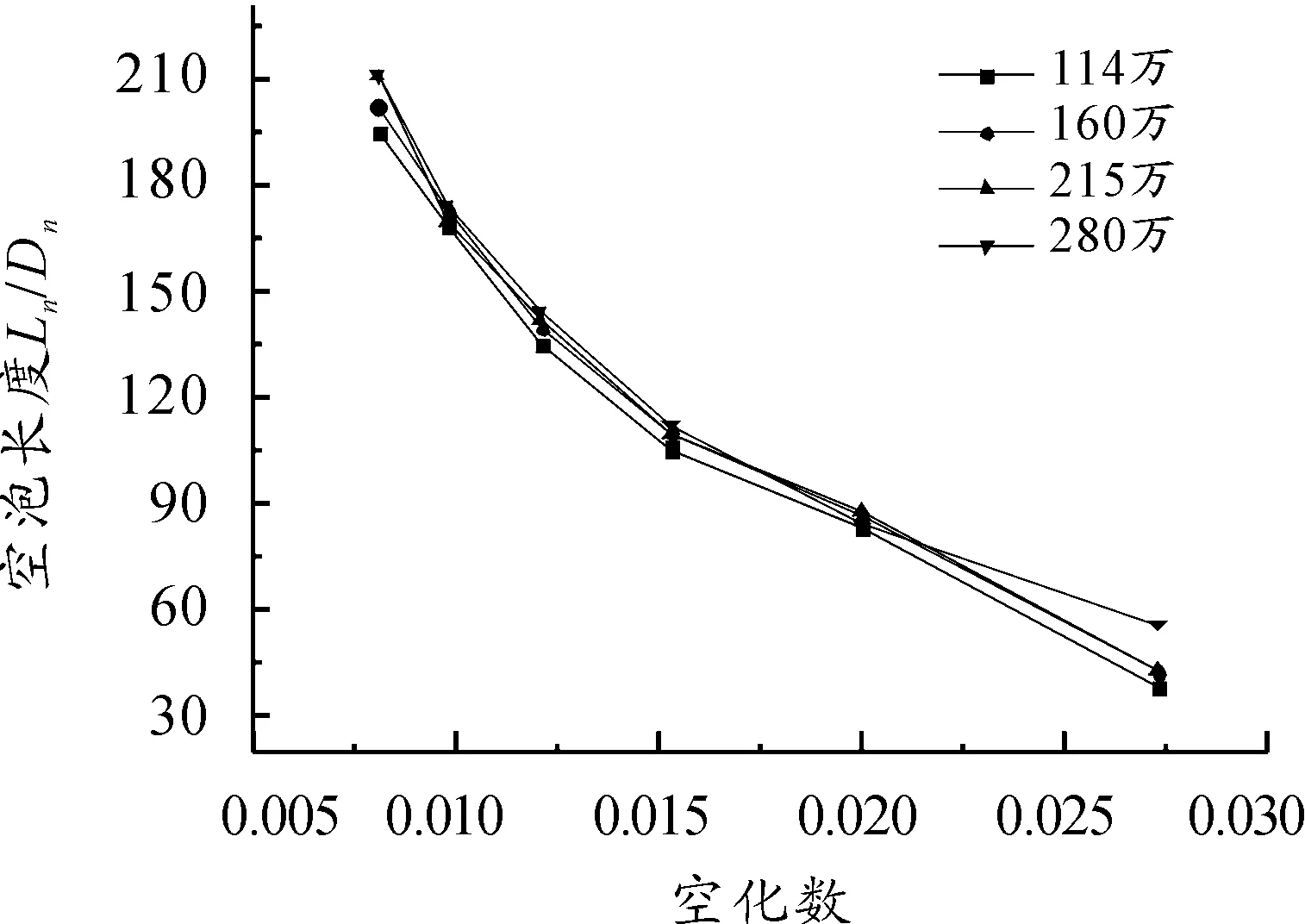
图3 空泡长度随空化数的变化

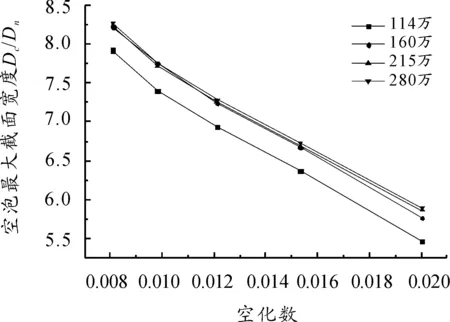
图4 空泡宽度随空化数的变化

图5 流场速度分布示意图

2.2 数值计算结果验证方法

为了验证选取数值计算方法的准确性，本文选取了乌克兰国家科学院IHM积累的带圆盘空化器模型自由运动的空泡形状计算公式

(19)

(20)

以及Logvinovich的空泡截面独立扩张原理式。Logvinovich在文献[6]中给出了空泡的最大半径和半长的半理论、半经验计算公式，本文取空泡全长和最大截面直径，将其修正如式(21)、式(22)所示。

(21)

(22)

通过计算可知，式(19)的计算结果和式(21)对空泡最大截面计算值相差最大可以达到11.77%，对于空泡长度的计算值相差可以达到23.32%。然而，乌克兰国家科学院IHM的经验公式是建立在大量水洞和敞水试验基础上的，而Logvinovich空泡截面独立扩张原理又是目前公认的描述超空泡流最为准确的计算方法。因此，为了得到较为准确的验证结果，利用数值优化软件，对上述公式分别进行6次多项式数值拟合，确定系数R分别为0.994 14和0.999，拟合得到无量纲空泡最大截面直径Dc/Dn计算式和无量纲空泡长度Lc/Dn计算式如下，其结果分别如图6、图7所示。

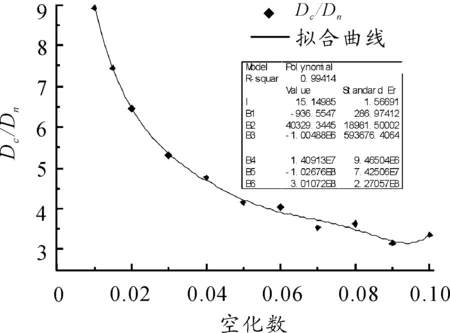
图6 Dn/Cn的拟合结果

(23)

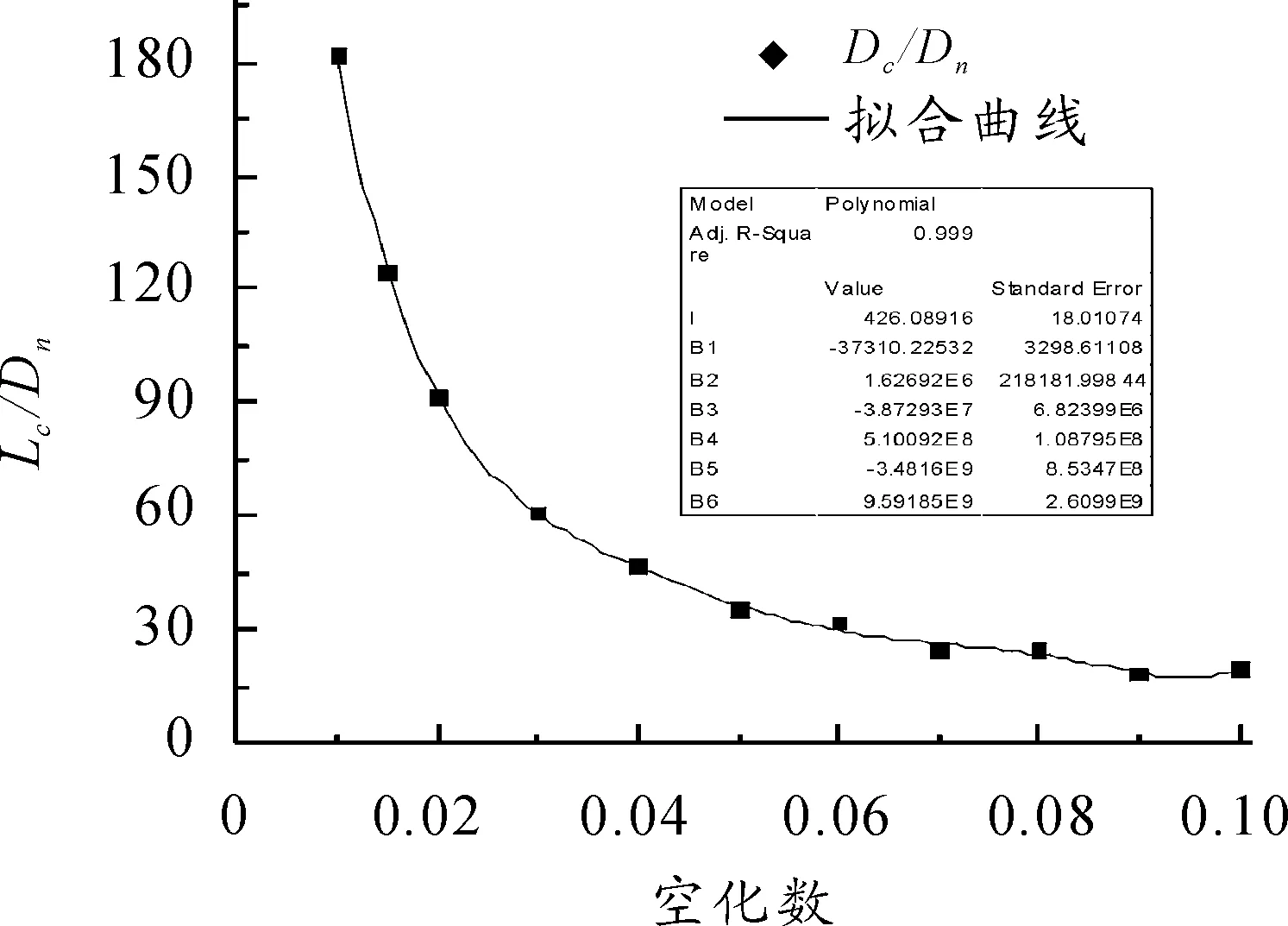
图7 Ln/Dn的拟合结果

(24)

通过将CFD软件计算得到的空泡形态参数与拟合得到的结果(式(23)和式(24))进行对比，得到数值计算误差，进而确定准确的数值计算模型。

如表2和表3给出了拟合结果与乌克兰国家科学院IHM的经验公式与Logvinovich空泡截面独立扩张原理关于空泡形态计算公式的计算结果对比，表明拟合结果关于无量纲空泡最大截面直径Dc/Dn的误差均小于8%，关于无量纲空泡长度Lc/Dn计算结果的误差小于11%。通过计算结果与拟合结果进行对比，充分考虑了两类经验公式优势：试验数据丰富、理论完善，得到新的空泡形态计算公式可信度更高，数值计算验证方法也更为准确。

表2 Dc/Dn拟合结果与经验公式比较

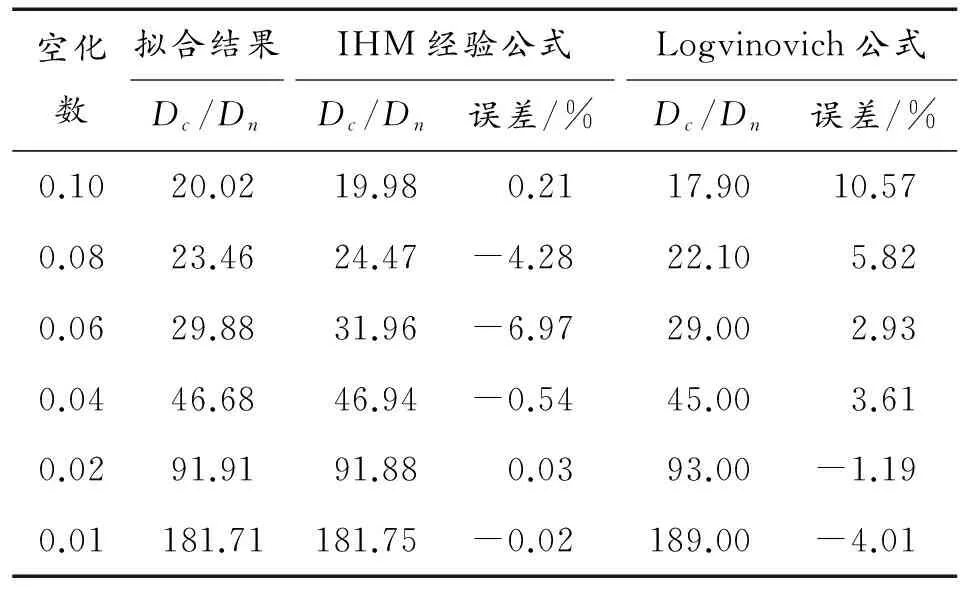
表3 Lc/Dn拟合结果与经验公式比较

2.3 空泡形态计算结果分析

对于超空泡航行体的数值模拟，由于涉及大量气液质量传输过程，所以数值模拟复杂程度较高，计算准确性难以把握。

表4给出了不同两方程模型下的数值空泡截面宽度的无量纲数值计算结果。从表中可以看到，数值计算得到的结果均小于由拟合经验公式计算得到的结果。图8给出了不同计算模型下空泡截面宽度的计算误差随空化数的变化关系，当空化数小于0.02时，数值模拟的精度较高，Kω-Sst模型的计算结果误差基本上小于14%，相对其他计算模型准确度更高。

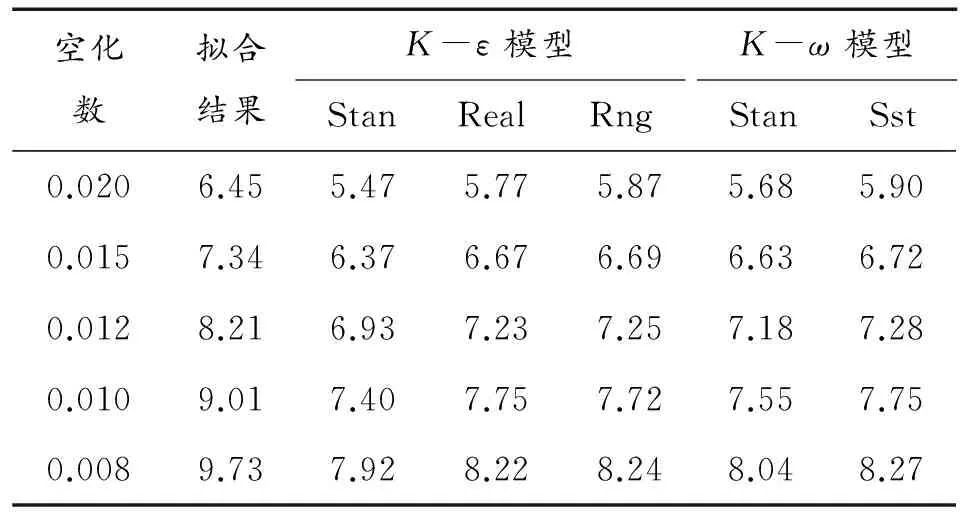
表4 Dc/Dn拟合结果与经验公式比较

由于本文中，设计数值试验为敞水试验工况，而经验公式的试验值及理论结果大部分均来源于水洞试验，计算结果受水洞影响较大。实际中，由于存在静水压力，对空泡截面宽度影响较大。所以，计算结果与经验公式存在一定误差。从图8可见，空化数在0.015～0.02时数值计算结果受其他因素影响较小，计算精度可以达到小于9%。

图8 空泡截面宽度计算结果误差对比

表5给出了不同RANS两方程模型空泡长度的无量纲(Lc/Dn)计算结果，不同计算模型下，空泡长度的计算结果均小于经验公式的计算值。相同空化数下，不同模型计算结果相差不大。图9比较了不同湍流模型空泡长度计算误差随空化数的变化结果，由图可见，在空化数小于0.01时，Kω-Sst模型和Kω-Stan模型的计算准确性较高，计算误差小于4%，当空化数大于0.01小于0.02时，Kω-Sst模型计算精度相比其他模型较高，可以保证小于8%。

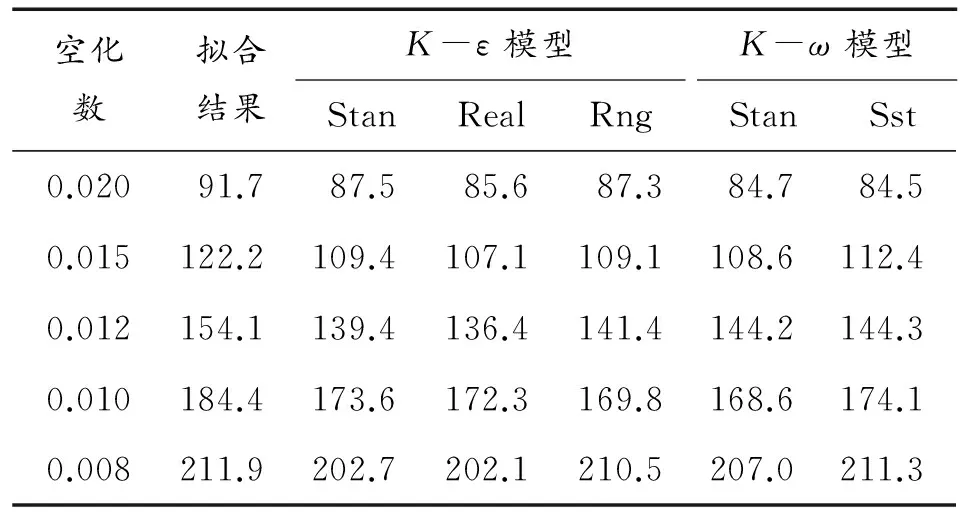
表5 不同RANS模型空泡长度的无量纲计算结果

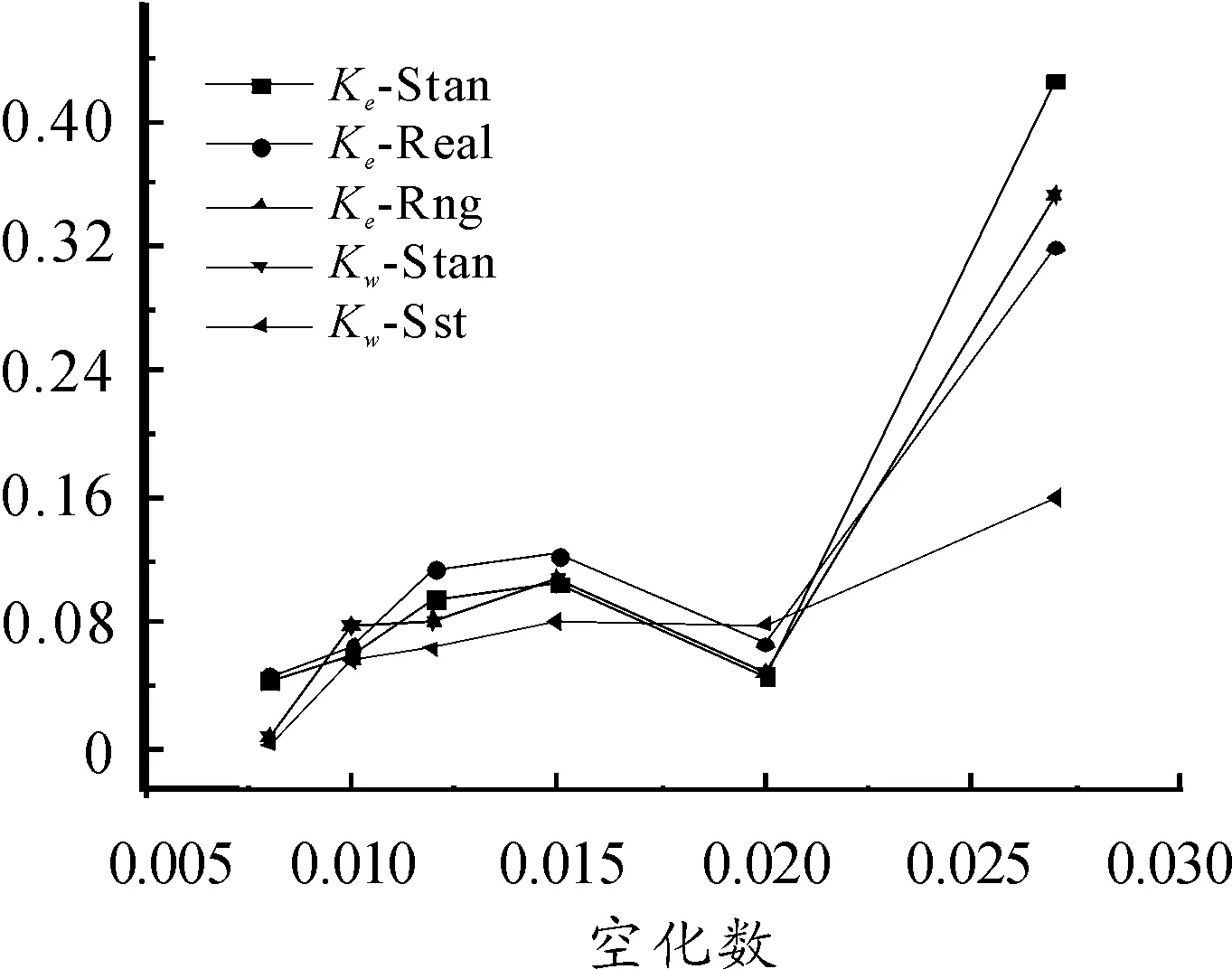
图9 空泡长度计算结果误差对比

比较不同RANS两方程空泡最大截面宽度的计算结果和空泡长度的计算结果可知，Kω-Sst模型更适用于超空泡航行体的数值模拟。

2.4 流场特性分析

基于建立文中确定的数值计算模型，选取精确度较高的Kω-Sst模型，水深10 m，空化数为0.015时，对超空泡航行体进行流场特性研究。

图10给出了超空泡航行体的艏部的空泡相分布云图和速度场云图，从图中可以得到当水在空化器锐缘附近汽化后流入超空泡内部，在空化器后部速度会急速增加达到100 m/s量级，在航行体艏部附近还存在一定的速度梯度，该速度梯度以及高速气流的存在严重影响超空泡的稳定性，对超空泡航行体的稳定运行造成影响，在超空泡航行体的设计中需要改良空化器或者优化航行体艏部形状，消除该速度梯度和高速气流区。

图10 超空泡航行体头部相分布云图(上)和速度场云图(下)

图11给出了超空泡航行体的压力场云图。从图中可见，由于无尾翼超空泡航行体在自然超空泡航行过程中只有艏部空化器与水接触，艏部空化器在空化数为0.015时需要承受压力为123个大气压。因此在对空化器设计的过程中，需要充分考虑承受压力对空化器的影响，尽可能地增大受压面积，采用高抗压材料，保证水下超空泡航行体运行安全。

图11 空化数为0.015时，超空泡航行体的压力场

图12给出了超空泡航行体的涡流强度分布，由计算结果可知，航行体尾部涡强度较大，在艏部区域以及尾流区域，涡通量达到最大。由于涡强分布，可以得到旋涡作用强度分布，进而可以定性的得到超空泡航行体运动过程中所受到的扰动作用强弱。

图12 超空泡航行体的涡流强度分布

3 结论

1) 基于乌克兰国家科学院IHM半经验公式和Logvinovich空泡截面独立扩张原理式，利用数值优化方法，建立了空泡形态数值计算验证模型。

2) 比较了RANS两方程模型对超空泡航行体数值计算结果，得到了Kω-Sst模型的关于空泡最大截面计算结果误差小于14%；对空泡长度的数值计算结果小于8%，空化数小于0.01时，小于4%。

3) 基于建立的准确性数值模型，对空化数为0.015时自然超空泡进行了流场分析，为超空泡航行体空化器的设计提出了改进意见。

[1] WEILAND C,VLACHOS P.Observation of a Critical Time Scale for Supercavi-tation Development and the Effect of Gas Leakage[C]//2008 ASME Fluids Engineering Conference.Florida USA,2008.

[2] 李凤臣,邹志林,蔡伟华,等.减阻剂水溶液内弹体入射超空泡特性实验研究[J].工程热物理学报,2010,31(5):857-862.

[3] WU T Y.A Free Streamline Theory for Two-Dimensional Fully Cavitated Hydrofoils[J].Journal of Mathmatical Physics,1956:236.

[4] SINGHAL A K,LI H Y,ATHAVALE M M,et al.Mathematical Basis and Validation of the Full Cavitation Model[C]//ASME FEDSM’01.New Orleans,Louisiana,2001.

[5] SEREBRYAKOV V V.Ring Model for Calculation of Axisymmetric Flows with Developed Cavitation[J].Journal of Hydromech,1974(27):25-29.

[6] SEREBRYAKOV V V.Some Models of Prediction of Supercavitation Flows based on Slender Body Approximation[C]//Proceedings of the Fourth International Symposium on Cavitation.Pasadena,USA,2001:sessionB3.001.

[7] 高强,张宇文,陈伟政.基于细长体理论的超空泡外形估算[J].弹箭与制导学报,2005,25(2):373-376.

[8] QIAN ZHONGHUA,HUANG SHEHUA.Comparison and analysis of computed results for cavitating flow with four turbulence models[J].Advances in Water Science,2006,02:203-208.

[9] HU QINGQING.Experimental Observation And Numerical Calculation Of Supercavity Flow Of Blunt Body Under Different Inclination Angle Into The Water[D].Zhe jiang:Zhe jiang Sci-Tech University,2014.

[10]XING YANJIANG.Research on hydrodynamic characteristic of vehicle unsteady cavity flow[D].Harbin:Harbin Institute of Technology,2013.

[11]赵怡，刘平安，苗成林.非稳态超空泡流动的数值模拟[J].四川兵工学报，2015(1): 64-67．

(责任编辑 杨继森)

Supercavitation Research on Numerical Simulation Method Based on Two-Equation RANS Model

DU Pei-pei, XIAO Chang-run, ZHANG Lu, ZHENG Wen-long, JIAO Yu-chao

(Department of Naval Architecture Engineering, Naval University of Engineering, Wuhan 430033, China)

In order to get the accurate numerical simulation method, the calculation model of supercavity shape was established based on the semi-empircal formula of supercavity form in Institute of Hydromechanics of National Academy of Science in Ukraine and the Logvinovich principle of independent expansion of cavity section. By using the finite volume method, the nelerical discretization method of supercavitation flow was authenticated and the supercavitation flow with five different two-equation RANS model was calculated in different cavitation number. The simulated results indicate that the accuracy of the calculation results ofKω-Sstis higher compared with other models. The complutational error of the dimensionless maximum diameter of the supercavity can be maintained at less than 14%. And the calculation error of the cavity length can be reduced to less than 8% and the error can be futher reduced to 4% when the cavitation number is less than 0.01. Based on the established mathematical model, the flow performance of the supercavitation vehicle was calculated when the cavitation number is 0.015. The computed and analyzed results show that: there is a high-speed air flow area and obvious velocity gradients behind the cavitator. Hydrostatic pressure in the vicinity of cavitator can reach 123 atomosphere pressures and the improvement of the design of the supercavitation vehicle is proposed based on these calculation results.

supercavitation；turbulence model；finite volume method；CFD

2016-06-16；

2016-07-15

国家部委基金资助项目(51314010203)

杜佩佩(1991—)，男，硕士研究生，主要从事舰船流体力学研究。

肖昌润(1963—)，男，博士，副教授，E-mail：xiaochangrun@sina.com。

10.11809/scbgxb2016.10.037

杜佩佩，肖昌润，张露，等.基于RANS方法超空泡流数值计算方法研究[J].兵器装备工程学报，2016(10):174-180.

format:DU Pei-pei, XIAO Chang-run, ZHANG Lu,et al.Supercavitation Research on Numerical Simulation Method Based on Two-Equation RANS Model[J].Journal of Ordnance Equipment Engineering,2016(10):174-180.

TJ610.1

A

2096-2304(2016)10-0174-07