MEMS万向开关加工误差分析

邓 鹏，吴玉斌，郝永平

(沈阳理工大学 装备工程学院，沈阳 110159)



【机械制造与检测技术】

MEMS万向开关加工误差分析

邓 鹏，吴玉斌，郝永平

(沈阳理工大学 装备工程学院，沈阳 110159)

为了研究加工误差对万向开关响应阈值的影响，推导出了惯性开关响应阈值的计算公式，带入设计参数值计算得到的结果为391 g，对样品开关的实际响应阈值进行了冲击台跌落试验，实验结果220 g，误差-43.7%。对影响响应阈值的各项尺寸进行测量，其中S型悬臂梁的线宽B误差最明显，测量值26.4 μm，小于设计许可值30 μm，误差为-12%，由阈值公式，该误差引起的响应阈值误差高达-30%。最终得出结论，由于S型悬臂梁的线宽B尺寸较小，加工时容易产生较大误差，悬臂梁的刚度与线宽B的立方成正比，因此线宽B是影响开关响应阈值的主要因素。

MEMS；万向开关；响应阈值；尺寸测量；加工误差

惯性开关也称g值开关，能感知外界加速度信号，当加速度达到设计阈值时，开关内的电极会机械地闭合。因此惯性开关是兼具感知和执行功能的惯性器件。MEMS技术被运用于惯性开关后，使其体积减小，抗过载能力变强，且无源式MEMS惯性开关还具有抗干扰能力强的优点，这些优点使得MEMS惯性开关常被运用于引信中。体积小能节省空间，便于在引信中引入更多的模块，实现弹药智能化；抗过载能力强使其能满足弹药勤务处理的要求；良好的抗干扰能力有助于提高弹药的安全性和准确性。

1975年美国在国防专利中提出了一种惯性开关[1]，采用“弹簧-质量块”结构，质量块在外界加速度的作用下产生位移，与固定电极接触。但是作为传统机械，该开关不可避免存在一些缺点，如灵敏度不高，零件多，装配复杂，弹簧性能不稳定等。MEMS惯性开关的出现很好地克服了传统机械开关的缺陷。2002年日本的Tadao Matsunaga等人提出了一种运用于汽车安全气囊的惯性开关[2]，该开关密封于高压氮气中，利用气膜阻尼获得足够的接触时间。但是由于该开关对密封性要求高，限制了其批量生产与运用。2002年美国的Robinson等人提出了一种基于方形电极的万向开关[3]，该开关能感知平面内任何方向的加速度信号，但是电极在各方向的间隙不一，使响应一致性不好。2001年韩国高新技术研究所提出了一种阈值可调的MEMS惯性开关[4]，该开关利用静电力和惯性力的共同作用使电极闭合，通过调节预加电压达到阈值可调的目的，缺点是需要持续供电，抗干扰能力差。国内杨卓青等人提出了一种非硅衬底的MEMS惯性开关[5]，将固定电极做成薄的弹性梁，将可动电极与固定电极的接触由刚性变为柔性，配合非硅衬底，虽然避免了猛烈回弹对电极造成的损坏，但是增加接触时间的效果不明显。后来出现了环形万向开关[6]，该开关固定电极也采用悬臂梁支撑，有效增加了接触时间，打破了“可动电极-固定电极”的模式。该开关将电极设计为圆形，使得开关各方向阈值一致，缺点是电极接触面积小，接触电阻大。万向开关的支撑方式有内支撑和外支撑之分[5-7]，外支撑是由若干根悬臂梁从电极外部将其撑起，电极悬于中间，内支撑则是悬臂梁从电极内部空隙处将其撑起，两种支撑方式可灵活选用。虽然目前出现了能满足各种要求的惯性开关结构，但由于国内MEMS工艺尚不成熟，要使开关投入工程运用，就不能忽视加工误差对开关性能的影响，一定要提高其加工精度。MEMS惯性开关的性能一般由响应阈值、响应时间、接触时间等技术参数决定，其中响应阈值对加工误差比较敏感。本文针对一种MEMS万向开关[6]，分析影响其相应阈值的参数，并对其进行冲击台实验，尺寸测量，探究加工误差和阈值误差间的关系。

1 万向开关结构及工作原理

万向开关主要由内、外电极，锚区及限位块组成，如图1所示。采用准LIGA工艺(利用紫外光刻设备和掩膜在光敏材料上光刻形成模子，再电铸金属形成金属结构)加工，材料为镍。内电极为圆环形，由固定在锚区A的四根S型悬臂梁从内部支撑并悬空；外电极同样为圆环形，由固定在锚区B的四根S型悬臂梁从外部支撑并悬空；限位块位于外电极四周，主要起防止电极位移过大造成悬臂梁失效。内电极质量较外电极大的多，是“弹簧-质量块”系统中的核心部分，能有效感知X-Y平面的加速度载荷，并向着载荷方向移动。当载荷足够大时，内、外电极接触，由于外电极也由悬臂梁支撑，所以是柔性接触，保证了足够的接触时间。锚区A、B都连接有向外部的引线。

2 影响阈值的参数分析

万向开关是典型的“弹簧-质量块”系统，开关的运动控制方程为[7]：

(1)

式中，c为阻尼系数，m为质量块质量，k为弹簧刚度，a(t)为加速度，由于开关中阻尼为滑膜阻尼，可忽略不计。内电极质量远大于内电极，因此内电极的质量、支撑内电极的悬臂梁刚度和内、外电极的间隙是决定开关阈值的主要因素。悬臂梁的某些参数对其刚度的影响是非线性的，是研究的重点。

图1 万向开关结构

通过材料力学能量法中的卡氏第二定理[8]，先取一节悬臂梁计算其刚度，再推广到n节悬臂梁。从而节数为n的S形悬臂梁在X、Y方向上(如图2)的刚度为[9]：

Kx=EB3T/8nLB2+72πR3+

(2)

Ky=EB3T/n(16L3+96R2L+24πRL2+12πR3)

(3)

式中，E为材料的弹性模量，T为厚度，B为线宽，L为半节悬臂梁宽度，R为弯曲处中位半径，n为节数。

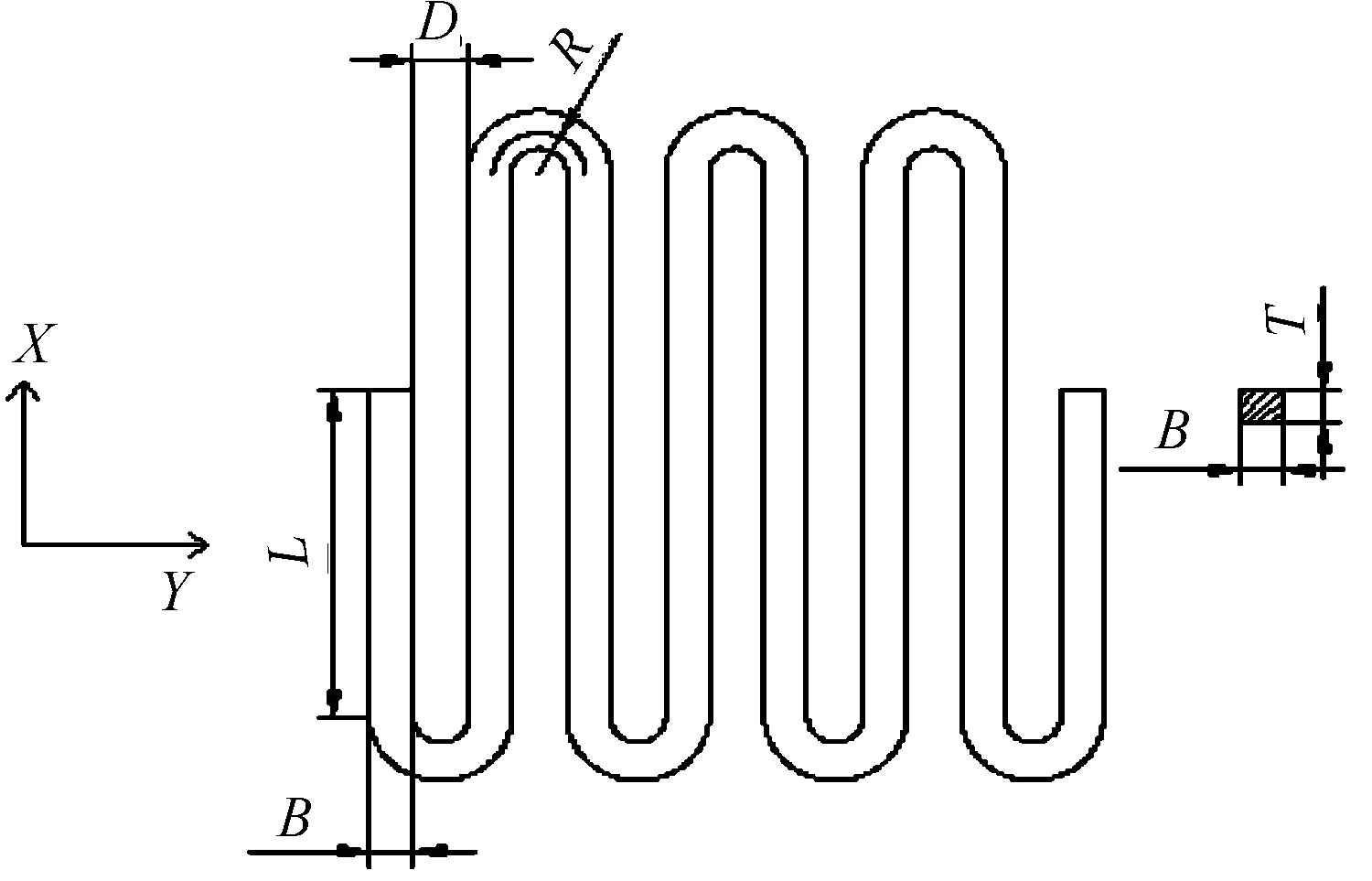
图2 S型悬臂梁简化图

如图1所示，四根S形悬臂梁组成一个弹簧系统，两个弹簧分别支撑着内、外电极。四根悬臂梁“十”字形的排列方式使得弹簧系统在X-Y平面内刚度保持一致。

弹簧系统的刚度为：

K=2Kx+2Ky

(4)

在外载荷的作用下，开关闭合，内、外电极位移之差正好等于间隙d。则响应阈值为：

(5)

将设计参数值(如表1)带入上述式(2)、(3)、(4)中，得K内=0.235 4N/m，K外=2.67N/m，已知m内=2×10-3g，m外=3.35×10-4g再由式(5)计算出响应阈值a0=3 832m/s2=391g。利用LS-DYNA软件对开关模型进行动力学仿真，开关的响应阈值为420g，计算值与动力学仿真值相比，其相对误差为7%。虽然式(5)对实际情况做了一定的简化，但是并未出现较大的相对误差。

表1 内电极支撑梁设计参数值

3 万向开关冲击台实验

本次万向开关的加工样品由大连理工大学提供，封装后的开关样品如图3所示，开关安装在电路板上，内、外电极通过引线与外接插头连接，便于将开关接入实验电路，如图4。将电路板接入实验电路后通过夹具固定在冲击台上，由电路板检测开关是否闭合。调整冲击实验台的高度，即可得到不同的冲击加速度，该加速度由传感器检测并显示在与之相连的计算机屏幕上。能使开关闭合的最小加速度即是开关的阈值，对开关X-Y平面内各个方向阈值进行检测并取平均值，得到开关在X-Y平面内的阈值为220 g，与设计参数代入式(2)、(3)、(4)、(5)计算得到的响应阈值391 g相比，误差为-43.7%。

图3 万向开关样品

图4 实验电路板

4 尺寸测量

由式(5)可知，响应阈值由为内外电极间隙d、m内、m外、K内和K外决定，因为内电极质量远大于外电极，由式(4)可以看出K内对响应阈值的影响远大于K外，从式(2)和(3)可以看出，B，L和R对刚度的影响很显著，是非线性的，内电极的B，L和R是尺寸测量的重点。

图5 某悬臂梁的线宽B测量

测量结果如表2所示，

表2 内电极支撑梁线宽B尺寸测量

图6 某悬臂梁的折叠间隙宽度D测量

表3 内电极支撑梁弯曲处的中位半径R尺寸测量

图7 某悬臂梁的半节宽度L测量

内电极支撑梁半节宽度L尺寸测量结果如表3所示，

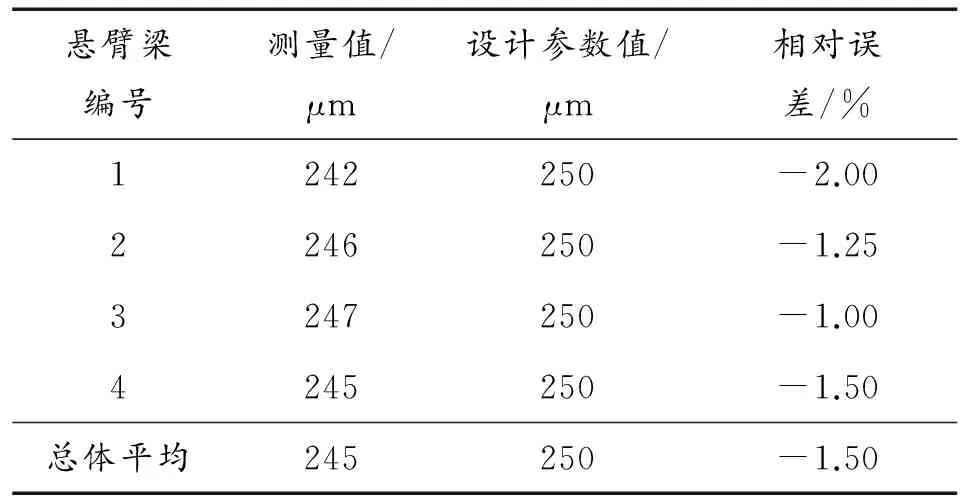
表4 内电极支撑梁半节宽度L尺寸测量

将悬臂梁线宽B、弯曲处中位半径R、半节悬臂梁宽度L的测量值和T、d、m内及m外的设计参数值代入到式(2)、(3)、(4)、(5)中，得到响应阈值a0=266 g，与全部设计参数值代入计算得到的响应阈值391 g相比，B值、R值、L值对响应阈值造成的相对误差达到-32%。

从表2、表3、表4所显示的B、R、L的测量结果看，三个参数中B的加工相对误差比其他两个参数R和L加工相对误差明显要大得多，这是由于线宽B本身绝对尺寸小和准LIGA工艺(利用同步电磁辐射X光进行光刻腐蚀、电铸成形的微制造工艺)的加工特性所造成的。当仅有B的测量尺寸代入，其余参数为设计参数值时，得a0=274 g，则B单独造成的阈值相对误差为-30%，占总相对误差-43.7%的68.6%，因此内电极线宽B是造成阈值相对误差的主要因素。

而实际阈值220 g与全部设计参数值代入式(2)、(3)、(4)、(5)计算得到的响应阈值391 g相比的误差为-43.7%，除去线宽B、弯曲处中位半径R、半节悬臂梁宽度L造成的误差，剩下的误差是由厚度T、内外电极间隙d、内、外电极质量m内及m外相关参数的加工误差以及理论计算与实际情况的差别造成的。

5 结论

1) 本文针对一种具有柔性电极的MEMS惯性万向开关，通过悬臂梁的刚度公式，得出了惯性开关的响应阈值公式。

2) 对惯性开关的响应阈值和加工尺寸进行了实验测量，悬臂梁线宽B平均误差为-12%，中位半径R和半节宽度L的平均误差仅为-1.5%，线宽B容易出现较大误差。

3) 通过阈值公式对各项测量参数进行分析，得出内电极悬臂梁线宽B的加工误差是影响开关阈值误差的主要因素，占总误差的68.6%。且从测量结果来看，准LIGA工艺目前的加工误差散布还是比较小的，因而今后在提交加工图纸时可以对B、R、L的尺寸分别进行+12%、+1.5%、+1.5%的补偿，使开关成品的响应阈值更加接近预期的数值。

[1]JENKINSBM,CHATHAMNJ.Inertialimpactswitchwithnormallycentered,conductiveoscillatingcontact[P].US:3899649,Aug.12,1975.

[2]TADAOMATSUNAGA,MASAYOSHIESASHI.Accelerationswitchwithextendedholdingtimeusingsqueezefilmeffectforsideairbagsystems[J].SensorsandActuators,2002,A100:10-17.

[3]ROBINSONCH.Microelectromechanicalsystems(MEMS)-typehigh-capacityinertial-switch-chingdevice[P].US:6314887B1,Nov.13.2001.

[4]HUANGJM,LIEWKM,WONGCH.Mechanicaldesignandoptimizationofcapactivemicrom-achinedswitch[J].SensorsandActuators,2001,A93:273-285.

[5] 杨卓青，丁桂甫，蔡豪刚，等.基于非硅表面微加工的MEMS惯性开关设计与动力学仿真[J].功能材料与器件学报,2008，14(3)：629-633.

[6] 刘双杰，郝永平.环形无源万向微机电惯性开关[J].中国惯性技术报,2013,21(2)：240-244.

[7] 席占稳，张平，聂伟荣.圆形质量块/柔性电极MEMS万向触发开关[J].探测与控制学报,2013，35(2)：10-14.

[8] 刘双杰，郝永平.S型折叠式悬臂梁刚度计算[J].光学精密工程,2013,21(2)：388-393.

[9] 杨伯源.材料力学[M].北京：机械工业出版社，2002.

(责任编辑 唐定国)

Analysis of Fabracation Error on MEMS Om-Nidirectional Trigger

DENG Peng, WU Yu-bin, HAO Yong-ping

(School of Equipment Engineerring, Shenyang Ligong University, Shenyang 110159, China)

In order to study the infulence of fabracation error on MEMS omnidirectional trigger’s response threshold, we deduced the calculation formula of inertia switch response threshold. We introduced the design parameter values, and calculated and got the result 391 g. We measured the actual response threshold of the trigger samples through impact table drop test. The experimental result was 220 g, and the result calculated through the design values was 391 g, and the error between them was -43.7%. The fabracation error of the S-shape beam’s line width is the most obvious, and the measured value is 26.4 μm and the design value is 30 μm, and the error between them is -12%, and this error can cause -30% errors in response threshold. The conclusion is that because of the line width B’s obvious error is caused by small size and theremarkable influence of line widthBon S-scale bean’s angular rigidity, the line widthBis the main influence factor of omnidirectional trigger’s response threshold.

MEMS；omnidirectional trigger；response threshold；size measurement; fabracation error

2016-04-15；

2016-05-20

邓鹏(1992—)，男，硕士研究生，主要从事MEMS器件设计与仿真研究。

10.11809/scbgxb2016.10.023

邓鹏，吴玉斌，郝永平.MEMS万向开关加工误差分析[J].兵器装备工程学报，2016(10):110-113.

format:DENG Peng, WU Yu-bin, HAO Yong-ping.Analysis of Fabracation Error on MEMS Om-Nidirectional Trigger[J].Journal of Ordnance Equipment Engineering,2016(10):110-113.

TJ430

A

2096-2304(2016)10-0110-04