基于极大似然目标状态估计的传感器管理

吴 蔚,熊朝华, 许 莺，王建宏

(信息系统工程重点实验室,南京 210007)



基于极大似然目标状态估计的传感器管理

吴 蔚,熊朝华, 许 莺，王建宏

(信息系统工程重点实验室,南京 210007)

为估计目标运动的状态估计量，设计相应的传感器管理方案，文章依据贝叶斯概率知识，采用极大似然的最优化方法来估计目标运动的状态估计值；依据目标状态估计的误差协方差矩阵与其Fisher信息矩阵间的联系，推导似然函数关于目标状态各个分量的偏导数；采用随机离散时间系统知识，推导出对角式Fisher信息矩阵所有对角线上的各个元素；以Fisher信息矩阵的迹范数作为传感器管理中的最优代价函数，采用0-1整数规划算法来求解传感器的分配矩阵；最后将极大似然的目标状态估计及其相应的传感器管理方案应用于无人直升机的飞行控制系统中，以验证本文方法的有效性。

目标状态估计；极大似然；协方差矩阵；传感器管理

0 引言

目标跟踪的目的是利用传感器的观测数据来估计目标的运动参数，包括目标的位置和速度等信息。目标跟踪可定义为已知目标的某些先验概率信息，在视频观测序列中连续获取目标运动信息(如位置、速度和尺寸等)的过程。这些运动信息即可作为目标运动过程中的状态变量。对目标运动状态的估计，可用于对所感兴趣的目标进行检测，精确捕获目标之后将其转化为自动跟踪模式，便于对目标属性进行评估、分类和识别；目标状态的估计仍可应用于下步的飞行控制器设计过程中。在目标跟踪、目标状态估计、目标定位检测过程都需要利用到传感器所采集到的各种观测信息，而传感器的布局设计与传感器系统的资源都是有限的，在通信数据链的通信带宽和传输能量等方面也常常受到众多因素的限制。因此传感器的布局管理技术是目标跟踪性能的首要基础问题。

目标跟踪是强调对目标状态的融合估计与预测对被跟踪目标进行在线建模，获得准确的当前目标状态，并对未来一段时域内目标状态进行预测。对目标状态的融合估计已研究得非常透彻，已提出较多的融合估计方法。如对线性系统的卡尔曼滤波法；对非线性系统的无色卡尔曼滤波法；可同时适用于线性或非线性系统的粒子滤波法等。因传感器管理是服务于下步的目标跟踪、目标状态估计以及飞行控制系统设计，所以传感器管理设计方案的优劣可通过其服务最终目的来体现。基于此思想，可从目标状态估计的准确度方面来设计传感器方案。对于所建立的目标运动方程，采用卡尔曼滤波算法得到目标运动时的状态估计及其相应的协方差矩阵。构造关于协方差矩阵的某个矩阵范数，通过此范数的最小化来得到最优的传感器设计方案。

基于最小化方差矩阵某范数的设计原则，文献[1]研究基于Riccati方程与Kuhn-Munkres算法相结合的传感器跟踪资源分配；文献[2]从流形中的Fisher信息距离之间的区分度来制定传感器资源分配策略；文献[3]利用粒子滤波器逼近目标状态，并估计协方差矩阵，实现传感器节点在线选择；文献[4]根据滤波后的目标误差协方差与不同战场态势下的期望之间的差异，利用模糊物元分析法控制传感器实现对目标的探测。文献[5]针对传感器管理设计中出现的最优化问题采用经典运筹学中的快速梯度算法来秋季，并分析此算法的迭代收敛性。文献[6]推导在某些工业闭环控制系统中，如何构造双闭环控制器可调参数辨识的方差矩阵。此方差矩阵的推导过程可应用于更为广泛的飞行控制系统中。

本文依然是采用基于目标状态估计的精度来设计传感器的管理方案。因目前已有的所有文献都是采用卡尔曼滤波算法来估计目标状态，仅仅简单地给出协方差矩阵的定义表达式。其中的各个目标状态和协方差矩阵也只是由其递推形式隐含地给出，而没有一个显式的表达式。本文绕开卡尔曼滤波算法的目标状态估计，构造极大似然的后验概率密度似然函数，通过最大化关于后验概率密度的似然函数来得到目标状态的一个显式解析解，且最优解可通过较为简单的一阶次快速梯度算法来求解。利用误差协方差矩阵的克拉美—劳下界公式，详细推导似然函数关于目标状态的一阶偏导数运算；通过复杂的矩阵运算过程得到Fisher信息矩阵的对角形式；依据协方差矩阵与Fisher信息矩阵间的紧密联系，构造传感器管理设计方案的最优化问题。

1 非线性状态空间的状态估计

以下首先给出本文提出的目标状态估计的极大似然法，以此状态估计值作为第3节传感器管理中的基础。因目标运动的动态系统可建模成含有隐性状态的状态空间模型，其隐性状态的部分信息可通过观测量来获取。状态变量可能含有移动目标平台的位置、速度和加速度等物理量，观测量可采用惯性陀螺等传感器来测取。考虑目标运动时的离散时间非线性随机系统为：

(1)

(2)

其中有：

∝p(y1:t|x1:t)P(x1:t)

(2)式中p(x1:t|y1:t)表示后验概率密度函数，p(y1:t|x1:t)表示似然，p(x1:t)表示先验概率密度。当观测量y1:t已知时，p(y1:t)也应是一个已知量。∝表示除去那些常数量后剩下的概率密度形式。

因观测方程中的观测噪声et为独立同分布的白噪声，即有：

似然p(yi|xi)为：

p(yi|xi)=pei(yi-h(xi))

利用全概率公式可得：

(3)

由马尔科夫性质可得：

(4)

重复应用(3)式和(4)式可得：

其中p(x1)表示在时刻t=1处初始状态的先验概率信息，由状态方程可知：

p(xi|xi-1)=pwi-1(xi-f(xi-1))

应用以上所定义的各个概率公式，可得(2)式中后验概率密度为：

(5)

从而(2)式所示的目标状态估计值为：

(6)

将wt和et的独立同分布高斯白噪声的假设条件应用于(6)式，可将3个概率密度函数展开，从而构成一个非线性的最小二乘问题，利用文献[5]中的一阶快速梯度算法求解(6)式，可得到极大似然意义下的最优目标状态估计值。

2 线性状态空间的状态估计

当(1)式中的f(xt)和h(xt)分别为线性函数特例时，可得到线性高斯型的状态空间模型。

其中的过程噪声wt和观测噪声et分别满足：

(7)

(7)式的含义表明：

(8)

将(8)式代入至(6)式中，并取负对数运算可得：

(2)

(10)

对(10)式所示的一阶偏导运算展开，可得t个等式。从这t个等式中可求解出最优饿目标状态估计值。由第2节和第3节的理论推导可知，目标状态估计的极大似然法是通过极大化似然函数的最优化过程而得，这是其与卡尔曼滤波算法的区别之处。当所构造出来的似然函数为凸函数时，由一阶快速梯度算法得到的最优解必是全局最优解，也即为目标状态的无偏估计。另外极大似然目标状态估计法还可用于关于目标状态的约束估计。即当假设概率密度函数px1(x1),pwi(wi),pe1(ei)为已知的对数形式时，约束的目标状态估计的最优化问题为：

(11)

3 传感器设计

3.1 协方差矩阵的计算

因传感器的管理设计方案是体现目标状态估计的精度，而状态估计的精度却是由估计的误差协方差矩阵来体现。为此本节首先分析极大似然目标状态估计的误差协方差矩阵形式。 由文献[6]可知，在(9)式中若利用泰勒级数展开，会使得协方差矩阵的计算过程异常复杂。因为需要计算(9)式似然函数的一阶和二阶偏导矩阵。但为减少算法的复杂度，可直接利用Fisher信息矩阵来构造目标状态估计的克拉美—劳下界，即：

(12)

由(12)式可见，在Fisher信息矩阵的计算过程中需要计算出如下的各个一阶偏导运算。

(13)

列出极大似然函数关于各个目标状态的一阶偏导矩阵为：

(14)

将(14)式代入至(2)式的Fisher信息矩阵的计算过程中，并在取数学期望运算时，利用过程噪声和观测噪声间的独立同分布性，可得到一个对角形式的Fisher信息矩阵。

(15)

利用对角矩阵的求逆运算，可到协方差矩阵的克拉美—劳下界为：

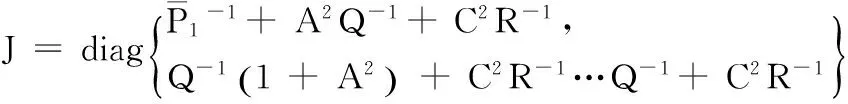
3.2 传感器管理的最优化

因在传感器的管理设计过程中，常设有m个目标，n个传感器。当考虑目标i对传感器j的目标状态估计的协方差矩阵时，以上的各个变量需要作对应的修改，用以强调是目标i对传感器j的协方差矩阵。此时可对应地表示为：

目标i对应的变量有：Ai, Ci

即目标i对传感器j的目标状态估计的协方差矩阵Pij为：

(16)

由文献[1]中的定义可知，目标i的优先级函数为pi，且pi∈[0,1]，当有命令指示作用于目标i时取pi=1，否则取pi=0。由传感器j对目标i执行任务时的价值函数Vij取为：

(17)

(17)式右边的各个量都是已知的，从而可简单地确定出价值函数Vij。定义目标—传感器分配矩阵为X，其元素为xij，当目标i与传感器j配对成功时取xij=1，否则取xij=0。为此将传感器的管理设计问题描述为一个最优化的传感器管理分配模型为：

(18)

(18)式中的两个约束条件分别保证每个传感器只能作用于一个目标和每个目标至少被一个传感器所执行任务。因(18)式中的最优化变量xij只能在0-1中取值，即(18)式为一个0-1整数规划问题[7]。关于(18)式的最优化求解可直接采用运筹学数学优化中的分枝有界算法。

4 仿真算例

将极大似然的目标状态估计及其相应的传感器管理方案应用于无人直升机的飞行控制系统中。无人直升机在空中飞行时呈现出六自由度的飞行姿态，包括仰俯、滚转和偏航3种飞行姿态。安装在无人直升机机身上的传感器为垂直陀螺，垂直陀螺为无人直升机飞行控制系统提供姿态角相关信息。垂直陀螺采用纵向安装方式，其结构示意图如图1所示。将陀螺的外环轴平行于无人直升机的纵轴，转子轴与地垂线重合，方向向上地安装[8]。

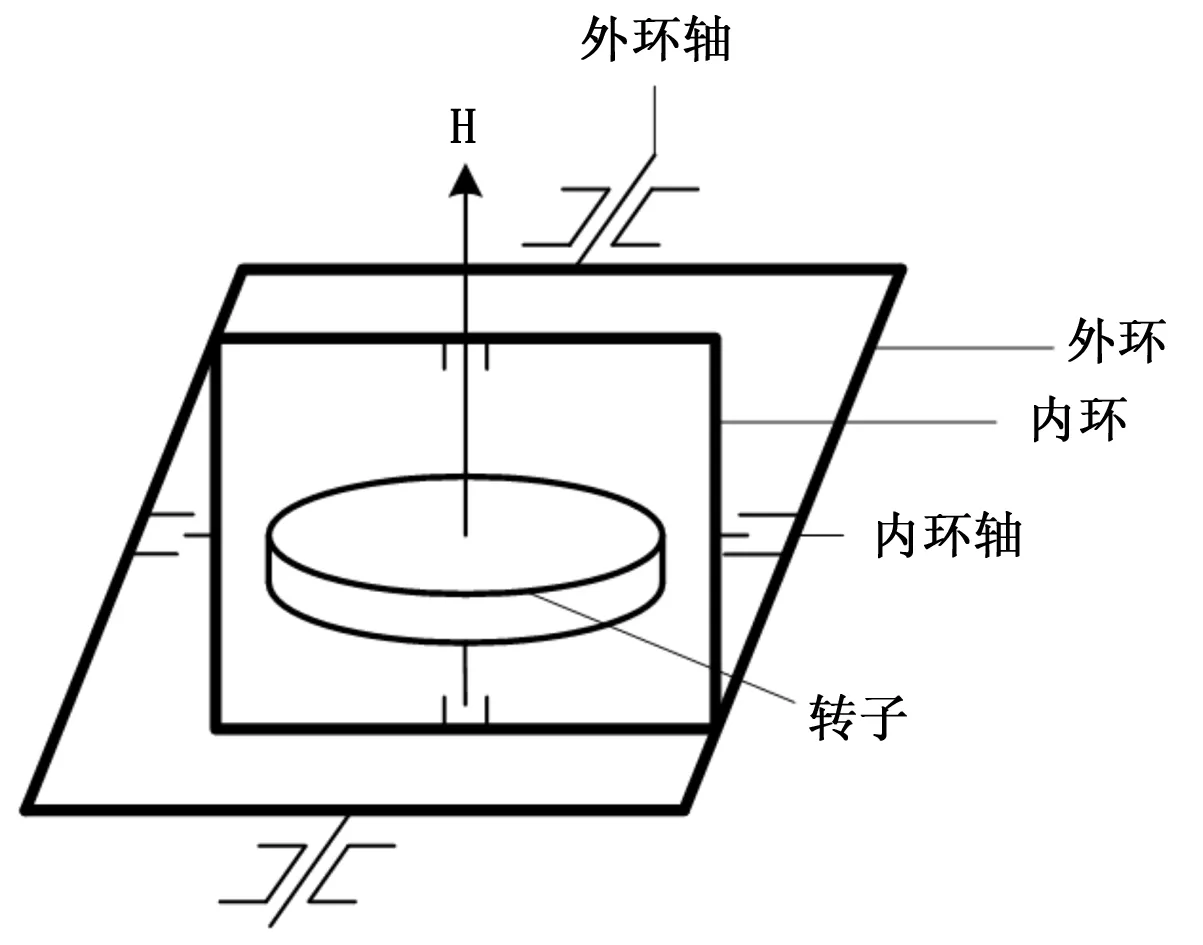
图1 垂直陀螺仪结构示意图

由垂直陀螺采集无人直升机在每次飞行过程中的各种观测信息，将采集信息通过数据通信链发送给测控站。在仿真中设定无人直升机的航迹：首先垂直定高5米，然后以5米/秒的上升速度垂直定高至100米，高度保持以40米/秒的前飞速度直飞，在100秒无人直升机以5米/秒的垂向速度下降，40米/秒的前飞速度下滑至50米高度继续前飞，仿真至300秒结束。仿真建模时，垂直陀螺针对于无人直升机的状态方程为：

xt+1=Axt+wt,yt=Cxt+et

(19)

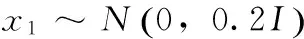
对(19)式的无人直升机运动方程应用基于最优化的极大似然目标状态估计策略，考虑垂直陀螺中也存在着白观测噪声，特别考虑无人直升机飞行状态的俯仰角变化，无人直升机模型输出的俯仰角、垂直陀螺仿真模型输出的俯仰角、滤波后俯仰角的最优估计如图2所示。

图2 俯仰角间的对比

图2中分别给出无人直升机的实际俯仰角、垂直陀螺的仿真俯仰角及其对应的比较图形。即图2(a)表示(19)式的期望目标状态，图2(b)表示由极大似然法得到的目标状态估计值，图2(c)表示期望值和估计值间的差异。

再次观测(19)式矩阵A的维数为6，状态的维数为6，可将其依次作为6个目标，即i=6。根据传感器管理最优化问题中的两个约束条件可知，垂直陀螺的个数不得少于6个，在仿真过程中可取j=6。在6个状态分量的目标中，选择目标优先级排序为：

T4≥T5≥T6≥T1≥T2≥T3

(20)

仿真过程中可安置6个垂直陀螺，关于垂直陀螺的内部结构、某些物理参数和各目标的价值函数等可参考文献[9] [10]。根据协方差矩阵的垂直陀螺最优化设计，各目标状态与各陀螺间的一一对应匹配见如图3所示。

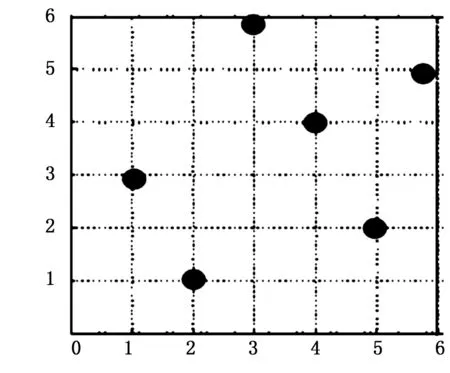
图3 垂直陀螺的分配图

5 结语

避开经典卡尔曼滤波目标状态估计需要大量的统计概率知识，采用极大似然函数得到目标状态估计的后验概率估计值，充分利用最优化的快速梯度算法。以极大似然目标状态估计值为基础，详细推导出误差协方差矩阵的克拉美—劳下界的Fisher信息矩阵式。以此Fisher信息矩阵的迹运算作为传感器管理分配的模型之中。因为传感器管理对应的是一个带有约束条件的0-1整数规划问题，对此最优化问题的求解还有待于更深层次的算法分析。

[1] 童 俊,单甘霖.基于修正Riccati方程与Kuhn-Munkres算法的多传感器跟踪资源分配[J]. 控制与决策, 2012, 27(5): 747-751.

[2] 张华睿,杨宏文.基于Fisher信息距离的传感器管理方法[J]. 系统工程与电子技术, 2012, 34(8): 1587-1591.

[3] 杨小君,马 祥.基于条件后验克拉美—劳下界的目标跟踪传感器管理[J]. 控制理论与应用, 2013, 30(5): 543-548.

[4] 崔博鑫,计蕴山.基于任务控制的动态多传感器管理方案[J]. 系统工程与电子技术, 2012, 34(2): 2473-2478.

[5] 王建宏.故障估计下子空间预测控制的快速梯度算法[J]. 上海交通大学学报自然科学版, 2013, 47(7): 1015-1021.

[6] 王建宏,许 莺.虚拟参考反馈校正控制的统计渐近性分析[J]. 计算机应用研究, 2015, 32(4): 1069-1073.

[7] Jacob Roll. Identification of piecewise affine systems via direct mixed integer programming[J]. Automatica, 2004, 40(1): 37-50.

[8] Fagiano L. Optimization of airbome wind energy generators[J]. International Journal of Robust and Nonlinear Control, 2012, 22(8): 2055-2083.

[9] 吴森堂,费玉华.飞行控制系统[M].北京:北京航空航天大学出版社,2005.

[10] 王惠南.GPS导航原理与应用[M].北京:科学出版社，2003.

Sensor Management Under Maximum Likelihood Target State Estimation

Wu Wei, Xiong Zhaohua, Xu Ying, Wang Jianhong

(Key Lab.of Information Systems Engineering, Nanjing 210007, China)

To estimate the state estimation about the considered target, and devise the corresponding sensor management, this paper uses Bayesian probability knowledge and maximum likelihood optimum method to estimate the target state estimation. This maximum likelihood method can not only solve the explicit solution of the target state with optimum strategy, but also deal with many constraints about the measurement and state variables. With the closed connection between the error covariance matrix and its Fisher information matrix, we derive the differentiation of the likelihood function with respect to each variable. Using some knowledge from stochastic discrete time system, we give every element which lies in the diagonal line of the diagonalized Fisher information matrix. The trace operation of the Fisher information matrix is applied to be the optimal cost function in the sensor management and then one 0-1 mixed integer numerical programming is used to obtain the sensor distribution matrix. Finally, we apply the sensor management under maximum likelihood target state estimation strategy into the flight control system of UAV in order to confirm the efficiency of the proposed strategy.

target state estimation; maximum likelihood; covariance matrix; sensor management

2015-08-17；

2015-11-11。

吴 蔚(1980-)，女，福建漳州人，主要从事信息融合与资源管理方向的研究。

熊朝华(1963-)，男，陕西西安人，研究员，主要从事信息融合方向的研究。

1671-4598(2016)03-0139-04

10.16526/j.cnki.11-4762/tp.2016.03.038

TP273

A