基于内罚函数的装备系统可靠性分配研究

李 锴，许世蒙，刘福胜，钱 潜，滕尚儒

(1.装甲兵工程学院 技术保障工程系，北京 100072； 2.装甲兵工程学院 基础部，北京 100072)



基于内罚函数的装备系统可靠性分配研究

李 锴1，许世蒙2，刘福胜1，钱 潜1，滕尚儒1

(1.装甲兵工程学院 技术保障工程系，北京 100072； 2.装甲兵工程学院 基础部，北京 100072)

装备系统可靠性分配的本质之一是有约束条件的非线性规划问题，从内罚函数角度出发，通过构造惩罚函数，将问题转化为无约束的优化问题；构造出基于装备系统复杂度和平均故障间隔时间的费用函数，将系统可靠度与费用关联起来，给出了在费用约束条件下的可靠性分配数学模型；在实例计算分析中，利用Matlab中的ode15s功能函数对分配模型进行计算，得到了不同惩罚因子下可靠性分配的最优解，计算结果具有较好的收敛性和稳定性，说明本分配方法具有良好的可行性。

可靠性分配；内罚函数；最优化 ；非线性规划

0 引言

为了落实装备系统的可靠性指标，在装备系统方案的论证阶段，就必须要求设计者逐级将产品的可靠性指标分解到各个不同层次的产品中，要求各级设计者明确其所研制产品的可靠性指标要求。在可靠性设计中，可靠性分配是指由上到下，从整体到局部，采用逐步分解的方式，将产品总可靠性指标分配到各系统、分系统及设备的过程[1-2]。

董聪[3]对系统可靠性分配的主要方法进行相关研究，主要包括等分配法、再分配法和比例分配法，并在此基础上提出了综合评分分配法，从本质上来说，此类分配方法均为无约束系统可靠性分配方法。宋保维等[4]从模糊数学理论角度出发，利用权重系数集合和确定隶属函数矩阵，将影响可靠性分配的多种因素综合考虑，给出了串联系统下可靠性的模糊分配方法，并进行算例验证，该方法简单、实用，具有一定的工程应用价值。张新贵等[5]通过设计自适应粒子群算法，在迭代过程中调整惯性权重系数ω，对航天测控系统进行任务可靠性分配，算例仿真的结果说明该方法具有分配结果优、收敛速度快等优点。

通常情况下，在进行系统可靠性分配的过程中，经常受到各种条件(如产品的费用、体积、研制周期等)的约束，要求系统在满足约束条件的情况下，使系统的可靠性指标尽可能高的分配。系统可靠性分配的方法随约束条件的侧重点不同而异，但是最终目的都是希望以最小的代价来满足系统可靠性指标。从本质上来讲，可靠性分配是一个综合权衡的反复迭代过程，在这种情况下，需要设计者考虑产品可靠性分配优化的问题。在满足应有约束条件的情况下，通过实现可靠性分配的最优化，达到甚至可能超过产品的可靠性指标。在可靠性分配计算过程中，可靠性分配优化问题可视为含有约束条件的非线性规划问题，由于约束条件通常具备多样性和非线性，故往往采用大多数传统经典的优化算法来求解该问题的最优解相对较困难[6]。

可靠性分配目前主要的方法主要有等分配方法、故障树分析方法、代数分配方法、动态规划法和直接搜寻法等等。随着可靠性数学模型越来越复杂，人们逐渐将多种人工智能方法运用到可靠性分配中，如：神经网络、遗传算法、模拟退火算法、人工免疫算法等，并且取得了部分成果，但已有的这些方法具有收敛速度较慢的缺点[7]。为了简化计算并实现优化目标，可以采用以下方法：1)将约束问题简化为无约束问题；2)将非线性规划问题简化为线性规划问题。采用罚函数(penalty function)方法，可以将有约束条件的非线性规划问题，转化为无约束的极值问题进行求解。该方法的主要求解思路为：将规划问题中的约束方程作为适当的惩罚函数，利用惩罚函数构造出含有参数的增广目标函数，此时问题转化为无约束的非线性规划问题，求解得到增广目标函数的极值即为可靠性分配的最优解。罚函数方法主要包含两种形式，外惩罚函数方法和内惩罚函数方法。外惩罚函数方法是从非可行域中的非可行解出发，然后到达可行域中可行解的过程，内惩罚函数方法是从可行解出发，在可行域中不断寻找最优解的过程。本文仅考虑费用这一项约束条件，构造出可靠度与费用的函数关系，该函数将系统复杂度和平均故障间隔时间(mean time between failures，MTBF)纳入考虑范围中，然后给出可靠性分配的数学模型，并利用内罚函数方法求解该非线性规划问题，得到的可靠性分配结果稳定收敛，为系统可靠性分配提供一种简单可行的方法。

1 可靠性分配数学模型

1.1 问题描述

可靠性分配是一个从上到下、由整体到局部不断进行分解的过程，主要是把装备系统的可靠性指标分配给系统、分系统直至元器件。可靠性分配的目的是让装备的各级设计人员明确装备的可靠性设计要求，通过可靠性设计与分析工作，将装备的可靠性要求设计到装备中去。研究装备系统可靠性分配问题是装备综合保障工程中重要的方面之一，使装备的研制与装备保障同步进行，摒弃过去采用的序贯式的研制方法，要求装备的设计与保障系统设计同步进行、协调发展。采用这种方式，可以较大程度地提高装备的完好性和可用性，并减少相关保障费用，尽快形成战斗力和保障力。可靠性分配结果是装备进行可靠性实验验证和装备系统评估的重要依据之一，对于装备设计研制具有重要意义。

在研究某装甲装备的工作中，需要考虑武器装备可靠性与费用之间的关系。该装甲装备主要结构示意图如图1所示，装备主系统主要包含5个分系统，分别为军械分系统、底盘分系统、电气分系统、三防分系统和指挥控制分系统，同时，不同的分系统又由不同的装置来构成，相对而言，底盘分系统的构造相对复杂，其次是军械系统和指挥控制系统。为简化计算，假设主装备为串联系统，各分系统相对独立，互不影响。g(x)代表装备分系统的可靠性与费用的函数关系，称为费用函数，x=(x1,x2…xj)为分系统的可靠度矢量，j为分系统的数目。在装备的实际设计研制过程当中，建立统一的费用函数g(x)要兼顾很多复杂因素与影响。事实上，统一的费用函数g(xj)是很难建立的，因为各分系统在结构、材料和加工工艺方面都各不相同，可靠性与费用不是严格的一一对应关系，并且关联数据的获取及处理均是复杂的理论与实际问题。

图1 某装甲装备系统结构示意图

随着作战需求的牵引和科学技术进步，武器装备得到飞速发展，一大批技术先进、成系列、结构复杂的武器装备被研制出来，其复杂程度和作战使用要求不断提高。为满足装备系统战备完好性要求，综合考虑装备的保障问题，在进行可靠性设计和分析工作时，需要设计者针对装备系统的复杂程度进行考虑。从装备系统设计的角度来讲，装备系统的可靠性可以分为基本可靠性和任务可靠性。基本可靠性是指装备系统在规定的条件下，无故障工作的时间或者概率[2]。系统平均故障间隔时间(MTBF)为用于系统设计和质量监控的常用基本可靠性合同要求，属于定量可靠性要求。对于可修复产品而言，MTBF的度量方式为：在规定的时间内和规定的条件下，产品的寿命单位总数与故障总次数之比[1-3]。将MTBF纳入到考虑范围当中，可以较好地衡量装备系统在对保障系统无需求情况下的工作能力，对于装备系统的设计研制具有指导意义。

根据同类相似装备的历史费用数据，采用类似比对的方式，可知费用函数g(xj)应当满足以下条件：

1)在主装备中，对于低可靠度(xj较小)的分系统而言，费用函数g(xj)较低；对于高可靠度(xj较大)的分系统而言，费用函数g(xj)较高，这是由于可靠度较高的分系统，其研发费用相对较高，故障率较低，在装备后续使用阶段，需要进一步支付的维修保障费用相对较低，因此其造价成本相对较高，即购置费较高。

2)g(xj)和g′(xj)均为单调递增函数，其中0≤xj≤1,j=1,2…m，这是因为随着装备分系统的可靠性要求不断提高，费用也不断增加；同时随着分系统的可靠度增加，尤其是可靠度增加到一定水平时，费用的增加速度越来越快，即g′(xj)也为单调递增函数。

根据以上分析经验，费用函数g(xj)可做如下近似处理[1,7-10]：

(1)

式中,aj和bj为经验参数，aj,bj>0，其中aj为g(xj)的变化速率参数，当可靠度xj较小时，费用函数g(xj)较小，同时g(xj)增加十分缓慢；随着可靠度xj增加，费用函数g(xj)逐渐增大，并且增加速度越来越快，即g′(x)为单调递增函数；bj为可靠度xj无限趋近于0时的费用，表示在可靠性设计中设计方案的费用；T为系统平均故障间隔时间。依据本文分析后给出的费用函数g(xj)，可以将分系统的复杂度和MTBF纳入考虑范围当中，与实际情况更加符合，对装备的可靠性分配以及分配结果的合理性具有一定的意义。

图2 费用函数g(x)的变化曲线

图2给出了费用函数g(xj)变化曲线，其中b=0。从图中可以看出：当经验参数a取某固定值时，参数T取值越大，费用函数g(x)越大，这是由于对于可修复的分系统而言，MTBF越大，在规定的时间和规定的条件下，该分系统的使用可用度相对较高，故障总次数相对较少，因此费用函数g(xj)相对较大；当参数T取某固定值时，经验参数a取值越大，则费用函数g(xj)越大，并且g(xj)的增速会越快，即g′(xj)越大。一般情况下，对于复杂程度相对较高的分系统，可以令其经验参数a取较大值，这是由于对于构造相对复杂的分系统而言，其组成装置相对较多，因而费用相对较高。从图2中还可以看出，在x=0.9附近左右，g(xj)增速非常快，这说明当可靠度增加到较高程度时，若要继续提高可靠度，费用会迅速增加。图2中的所有曲线说明，费用函数g(xj)随着分系统可靠度x具有相同的增长趋势，主要体现在g(xj)和g′(x)均为单调递增函数。为简化计算，本文在后面的讨论中，参数T取为固定常数T=500(小时)。

1.2 分配模型

在实际装备系统设计过程中，通常面临许多约束条件，例如在费用、体积、功率、研制周期等方面，均需要对装备系统提出相关约束条件。实质上，该问题可以归结为多目标多约束的优化问题，在多项约束条件下，我们要求设计的装备系统的可靠度最高；或者给出装备可靠性指标要求，在可靠性指标为约束条件的情况下，要求装备的其他参数达到最优化。在约束条件下进行可靠性分配时，为进行定量计算，将系统的可靠性指标和约束条件进行量化和相互联系，然后再进行可靠性分配及优化。通常情况下，装备系统可靠性分配的数学模型为[8-11]：

(2)

式中，Rs(x)为装备系统的可靠度；目标函数表示系统的不可靠度f(x)取最小值，约束条件中gi(x)为第i种资源的消耗总量，Ci为第i种资源的约束指标，i=1,2…n表示为多项约束条件。

对于图1所示的装备系统，根据假设各分系统相对独立，不会相互影响，装备系统为串联系统，在仅考虑费用的约束情况下，采用式(1)所示的费用函数g(xj)，装备系统可靠性分配的目标函数和约束条件为：

(3)

式中，xj为各分系统的可靠度，其中j=1,2…5。

实际上，依据本文的分析方法，也可以处理结构稍复杂一些的混联系统和具有一定相关性的复杂系统，只是在模型和计算实现方面要复杂一些。

式(3)为基于费用函数g(xj)的可靠性分配优化模型，该分配模型可归结为有约束的非线性规划问题，但采用通常的优化算法来求解x=(x1,x2…xj)相对困难。为简化计算并实现可靠性分配优化的目标，我们采用内罚函数的方法,可以将该含约束的非线性规划问题转换为无约束的极值问题，然后再进行求解，得到装备系统可靠性分配的结果x。

1.3 内罚函数[12-15]

针对式(3)所示的非线性规划问题，利用内罚函数方法求解可靠性分配问题时，将约束条件作为惩罚函数，将原目标函数与惩罚函数组合，构造出增广目标函数E(x,k)，称为能量函数。

定义如下函数：

(4)

(5)

式中，k为惩罚因子，k>0。

(6)

由于在式(6)的惩罚项中包含不可微函数max[0,φi(x)]，可采用近似处理办法，令：

(7)

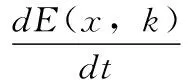
(8)

式中，μj为惩罚速率，μj>0。

1.4 分配求解

对于图1所示的装备系统，仅考虑费用的约束条件下，采用式(1)所示的费用函数g(xj)，定义如下函数：

(9)

式中,C为装备系统的总费用。

(10)

(11)

式(11)为仅考虑费用约束的情况下，基于费用函数g(xj)得到的装备系统可靠性最优分配的数学模型，该模型为常微分方程组，求解该常微分方程组，便可以得到主装备的可靠性分配结果x。

2 实例分析

2.1 实例参数

在式(11)的求解过程中，按照之前的分析，令T=500 (小时)。由于惩罚速率μ的取值仅影响分配过程的计算速率，并不影响最终的装备系统可靠性分配结果，为简化计算，令μ=(1,1,1,1,1)。对于惩罚因子k而言，若k过小，则能量函数E(x,k)的极小值点会远离稳定状态，分配结果的准确性较低，达不到可靠性分配最优的目标；若k过大，则会增加求解E(x,k)极小值的计算量，浪费计算时间，通常我们选取一组递增的序列{kω}来进行计算，然后会得到{xω}的结果。由于内罚函数方法具有稳定收敛的特点，因此{xω}最终的收敛结果x*就是可靠性分配的最优结果。

费用函数g(xj)中的经验参数aj和bj的取值如表1所示，对于复杂度较高的分系统，参数aj和bj的取值相对较大。

系统产品的总费用C=2 000(万元)，由于采用内罚函数的计算方法，该方法的特点是在可行域中不断搜寻，最终找到问题的最优解，因此我们首先需要给定一组可行域中的初值x0=(0.1,0.2,0.3,0.25,0.35)，由初值x0出发，然后分别计算惩罚因子序列{kω}=(0.001,0.005,0.01,0.05,0.1,1,10,1 000)下的可靠性分配最优结果。

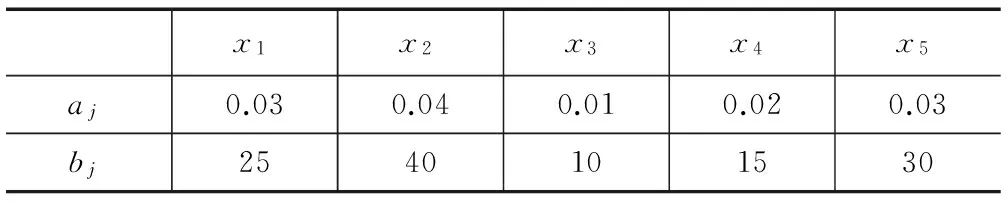
表1 经验参数aj和bj的取值

2.2 结果分析

在实际计算求解过程中，罚函数方法在Matlab中可以直接采用fminunc功能函数进行求解，但该方法存在不足之处，不能得到全局最优解，只能得到局部最优解，并且每次运行的结果均不相同[6,18]。由于所涉及的常微分方程组式(11)的初值问题为“刚性”问题，因此我们采用Matlab中的求解刚性常微分方程的ode15s功能函数进行求解，该算法计算结果准确度高，并且能得到全局最优解[18-21]。

表2为利用ode15s功能函数计算惩罚因子序列{kω}下的可靠性分配结果。

表2 惩罚因子序列{kω}下的可靠性分配结果

从表2的可靠性分配结果可以看出：

2)在k=0.01时已经达到最优分配结果，随着惩罚因子k继续增加，即使在k=1 000时，分配结果仍然稳定一致，没有出现波动，说明该分配方法稳定性较高。

图3 装备系统的可靠性分配结果

图3为当k=0.1时的装备系统可靠性分配结果。

从图3可以看出：1)随着计算步长t的增加，各分系统xi及装备系统的可靠度Rs曲线呈现迅速增加的趋势，说明计算速度很快；2)对于惩罚因子k=0.1，可靠度曲线在t=25附近达到最大值，随着t继续增长，各曲线的最大值保持不变，未出现曲线震荡现象，较为充分地说明了该可靠性分配结果是稳定收敛的。

3 结论

1)在仅考虑费用约束条件情况下，采用内罚函数方法，构造出含有参数的能量函数E(x,k)，利用Matlab中的ode15s功能函数求解可靠性分配的常微分方程组，实例验证说明该方法计算速度较快，分配结果稳定收敛。

2)在产品设计过程中，对于复杂度相对较高的分系统和设备，在进行可靠性分配时，通常分配较低的可靠性指标。这是因为分系统越复杂，其部件越多，要达到高可靠性指标相对困难并且费用较高，因此分配的可靠性指标相对较低一些，本文的实例验证结果也充分证明了这一点。

3)在构造费用函数g(xj)的过程中，将系统平均故障间隔时间(MTBF)纳入考虑范围当中，同时结合各分系统的复杂程度，得到了串联系统下考虑费用约束的可靠性分配数学模型。

可靠性分配可以作为一个演绎分解的过程，在实际的产品可靠性设计中，面临许多约束条件，如产品的重量、体积及功率等，依照本文的分析方法，采用内罚函数方法，可以综合多种约束条件同时进行可靠性分配工作；其中费用函数g(xj)中可以从多个角度同时进行构造，将故障率等可靠性参数纳入其中，同时考虑装备系统的重要度、装备工作环境的恶劣程度和采用的技术成熟程度，从而获得更准确的可靠性分配结果。从本质上来讲，可靠性分配可以看成一个综合权衡的优化设计的过程，对结构复杂的系统进行分配时，通常可以首先将系统按照结构简单的串联模型进行分析，当可靠性指标未能满足设计要求时，我们可以采用冗余的办法，对冗余部分再进行可靠性分配，最终达到系统的可靠性指标要求。

[1] 茆诗松，汤银才，王玲玲.可靠性统计[M].北京：高等教育出版社，2008.

[2] 曾生奎.可靠性设计与分析[M].北京：国防工业出版社，2013.

[3] 董 聪. 系统可靠性分配方法[J].系统工程与电子技术，1996,18(7):36-40.

[4] 宋保维，徐德民. 系统可靠性分配的模糊数学方法[J]. 西北工业大学学报,1998,16(2):271-275.

[5] 张新贵，武小悦. 基于自适应粒子群算法的航天测控系统任务可靠性分配[J].航空动力学报，2012,27(9):2147-2154.

[6] 邓乃扬,田英杰.数据挖掘中的新方法：支持向量机[M].北京：科学出版社，2004.

[7] Kuo W, Wan R. Recent advances in optimal reliability allocation [J]. IEEE Transactions on Systems, Man, and Cybernetics - Part A: Systems and Humans, 2007,37(2):143-156.

[8] 曹晋华，程 侃.可靠性数学引论[M].北京：高等教育出版社，2012.

[9] Kuo W, Prasad V R. An annotated overview of systems reliability optimization [J].IEEE Transactions on Reliability, 2000, 49(2):176-187.

[10] Nakagawa Y, Nakashima K. A heuristic method for determining reliability allocation[J].IEEE Transactions on Reliability, 1977, 26(3):31-38.

[11] Charles A O, Chu C B, Adiallah K H et al. Reliability Allocation Through Cost Minimization [J]. IEEE Transactions on Reliability, 2003, 52(1):106-111.

[12] 李海滨，段志信. 约束非线性规划问题的L1精确罚函数神经网络方法[J]. 电子学报,2009,37(1):229-234.

[13] Effati S, Baymani M. A new nonlinear neural network for solving convex nonlinear programming problems[J]. Applied Mathematics and Computation, 2005,168(2):1370-1379.

[14] Effati S, Jafarzadeh M. A new nonlinear neural network for solving a class of constrained parametric optimization problems[J]. Applied Mathematics and Computation, 2007,186(1):814-819.

[15] 连淑君. 近似逼近l1精确罚函数的罚函数[J]. 应用数学,2010,23(2):363-369.

[16] 陈海波,吕咸青,乔彦松. 梯度下降法在沉淀积物粒度分布拟合中的应用[J]. 数学的实践与认识,2011,41(13)：78-87.

[17] 高雪鹏,丛 爽. BP网络改进算法的性能对比研究[J]. 控制与决策,2001,16(2):167-171.

[18] 卓金武,李必文,魏永生,等. MATLAB在数学建模中的应用[M].北京：北京航天航空大学出版社，2011.

[19] Temesgen G, Lacy S. Modeling the influence of ethanol on the adsorption and desorption of selected BTEX compounds on bentonite and kaolin[J]. Journal of Environmental Sciences,2011,23(11):1865-1872.

[20] Holly M. MATLAB for Engineers Second Edition [M]. Pearson Education, 2012:348-383.

[21] 乔田田,李维国. 计算周期解时出现刚性问题的一种处理方法[J].计算物理,2007,24(3):367-372.

Application of Internal Penalty Function Method to Equipment System Reliability Allocation

Li Kai1, Xu Shimeng2, Liu Fusheng1, Qian Qian1, Teng Shangru1

(1.Department of Technical Engineering, Academy of Armored Force Engineering, Beijing 100072, China；2.Department of Fundamental Courses, Academy of Armored Force Engineering, Beijing 100072, China)

The problem of equipment system reliability allocation is nonlinear constrained optimization. Through the penalty function method, the problem of the cost restriction is transformed to non-restraint optimization problem. The fitting function is presented by the complex index and MTBF (mean time between failures) of the equipment, the mathematical model of system reliability allocation is established based on the fitting function between the reliability and the cost of the unit. The numerical solution was given with the ode15s function which fits the stiff function by the MATLAB software, the results show right convergence and stability when the penal factor was changing. This paper indicates that the internal penalty function method to system reliability allocation is feasibility.

reliability allocation; internal penalty function; optimization; nonlinear constrained optimization

2015-10-13；

2015-11-11。

李 锴(1990-)，男，山东淄博人，博士研究生，主要从事装备可靠性方向的研究。

1671-4598(2016)03-0118-04

10.16526/j.cnki.11-4762/tp.2016.03.032

TP3

A