无人水面艇航迹跟踪控制仿真

张 臣, 刘 收, 李宝安,3

(1.北京航空航天大学 自动化科学与电气工程学院，北京 100191; 2.北京航天测控技术有限公司，北京 100041;3.北京航空航天大学 无人驾驶飞行器设计研究所，北京 100191)



无人水面艇航迹跟踪控制仿真

张 臣1, 刘 收2, 李宝安1,3

(1.北京航空航天大学 自动化科学与电气工程学院，北京 100191; 2.北京航天测控技术有限公司，北京 100041;3.北京航空航天大学 无人驾驶飞行器设计研究所，北京 100191)

针对模型参数不确定、存在外界风浪流干扰的欠驱动无人水面艇的航迹跟踪问题，为提高无人水面艇自主航行能力，减小航迹跟踪过程中的轨迹偏差与跟踪迟滞，提出了一种分层控制结构的方法；由外至内采取航迹、航向、舵角三层控制，外环航迹控制层使用过渡目标点策略，根据无人水面艇的偏航距确定实时目标点，中环航向控制层使用最小转角策略，根据无人水面艇艏向角与目标方向角之差确定偏转打角，内环舵角控制层使用模糊自适应整定PID控制器，对模型参数的动态变化进行补偿；基于MATLAB GUI进行无人水面艇航迹跟踪控制仿真试验，结果表明，模糊自适应整定PID控制器提高了舵角的控制响应速度，无人水面艇在航行过程中的直线行驶、连续折线行驶均能得到较好的航迹跟踪控制。

无人水面艇；航迹跟踪控制；分层控制结构；模糊比例积分微分控制

0 引言

无人水面艇是一类能够实现无人自主操纵，具有自动感知、规划与航行能力的水面舰艇，主要用于执行不适于有人船只执行的军事或民用任务。

无人水面艇航迹跟踪控制是指在无人水面艇整体系统的作用下，使无人水面艇从预定的起始位置沿着指定轨迹一直航行到达目的位置。良好的航迹跟踪控制系统是无人水面艇工作的基础，能够为无人水面艇各项功能的实现提供基本保证，具有重要的应用价值。

1 航迹跟踪控制结构

1.1 航迹跟踪控制结构框图

航迹跟踪控制结构如图1所示，由3个闭环控制共同组成：外环航迹控制环、中环航向控制环和内环舵角控制环。

图1 航迹跟踪控制结构框图

外环航迹控制环将定位装置接收到的无人艇位置信息与预定航线进行比对。若无人艇位置不在预定航线上，则航迹控制算法根据航迹偏差进行运算，输出一个能消除航迹偏差的航向控制命令，作为中环航向控制环的输入。

中环航向控制环将姿态检测装置获取的无人艇实际航向与命令航向进行比对。若实际航向与命令航向存在偏差，则航向控制算法根据航向偏差进行运算，输出能消除航向偏差的舵角控制命令，作为内环舵角控制环的输入。

内环舵角控制环检测当前舵角，与接收到的命令舵角进行比对，若有偏差则驱动舵机伺服系统使实际舵角到达命令位置。

航迹跟踪控制系统通过3个闭环控制的共同作用，使无人艇在航行过程中消除航迹偏差，实现航迹跟踪控制。这种控制结构将位置控制与方向控制分离，捉高了系统的运行可靠性。

1.2 外环航迹控制层

假设无人水面船在航行过程中，海平面为二维平面，船的实时位置用经纬度表示。

假定船在某一时刻行驶某一指定航线，航线由起点A指向终点B，船的实时位置为点P。将船抽象为一个点，以船为中心，一定半径的圆内区域称为船的邻域。船的邻域位置由船的经纬度决定，船的邻域大小由邻域半径R决定，可表示为：

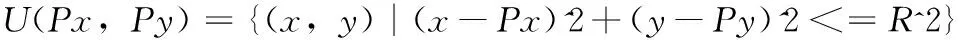
(1)

定义以航线起点A为中心、半径为R的圆为区域K1，以航线终点B为中心、半径为R的圆为区域K2，垂直于AB且与线段AB相交的所有直线组成的区域为K3，以K1、K2与K3的并集作为区域K。

如图2所示，区域K将整个平面分割为三块区域。当船在区域K中，认为船在当前航路行驶中。当船在区域K外且|PA|距离小于|PB|距离，认为船正在驶向当前航路。当船在区域K外且|PA|距离大于|PB|距离，认为船正在驶离当前航路。

图2 航域划分与航行状态区分

船的位置在航行过程中保持动态变化，根据船位置P的不同，实时的过渡目标点不同。

过点P作直线AB的垂线与直线AB相交于垂点Q，计算|PQ|的距离。连接PA、PB，并计算|PA|、|PB|的距离。求取目标点D作为中环航向控制环的输入：

1)Q在线段AB外，且R<|PA|<|PB|：

以A作为目标点D，驶向当前航路。

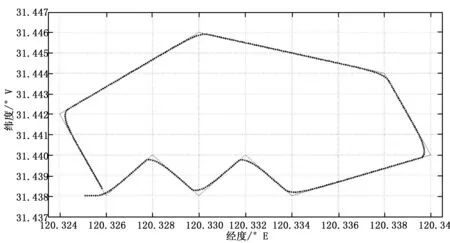
2)Q在线段AB外，且|PA|

P在A的邻域内，P邻域圆圆周交线段AB于M，以M作为目标点D。

3)Q在线段AB上，且|PQ|>R，|QB|>R：

P距离航路AB大于临界值R，Q作为目标点D进行航路修正。

4)Q在线段AB上，且|PQ|R：

P邻域圆圆周与线段AB相交于两点M1、M2，计算|BM1|、|BM2|并比较，取距离B点较远的一点M作为目标点D。

5)Q在线段AB上，且|QB|

P在B的邻域内，认为P已经到达当前航路终点，舍弃当前航路，若存在则装载下一航路，以B作为下一航路起始点，以C作为下一航路终点，重新进行航路规划。

6)Q在线段AB外，且|PA|>|PB|：

以B作为目标点D。当P进入B邻域，若存在则装载下一航路，以B作为起始点，重新进行航路规划。

1.3 中环航向控制层

船航行过程中，忽略真北与磁北差别。以真北为基准，顺时针旋转到船艏方向，定义转角为船的方向角。船的方向角α由姿态检测装置测量，范围为0°到360°。

船的位置和方向角在航行过程中保持动态变化。船的位置P与由外环航迹控制环解算的实时目标点D形成矢量PD，真北方向顺时针旋转到PD方向形成的角度可作为目标方向角θ，范围为0°到360°。

船的当前方向角α与目标方向角θ形成方向角偏差，Δα=θ-α，范围为-360°到360°。根据不同的Δα值，求取实际偏转方向角r：

(2)

1.4 内环舵角控制层

中环航向控制层解算的需求偏转角r作为内环舵角控制层输入，内环舵角控制层采取模糊PID进行舵角控制。

如图3所示为舵机模糊PID控制框图，r(k)作为系统输入，采集当前输出y(k)，则系统误差e(k)=r(k)-y(k)。根据前次e(k-1)和此次e(k)可得de(k)/dt。e(k)及de(k)/dt作为模糊控制器输入，经过模糊运算得到参数修正值ΔKp、ΔKi、ΔKd。e(k)作为PID控制器输入，Kp’、Ki’、Kd’作为控制器实际参数，输出舵机调节值。

图3 舵机模糊PID控制

PID参数整定结果为：

(3)

位置式PID离散表达式如下：

(4)

2 MATLAB GUI仿真

MATLAB GUI仿真可分为前台和后台两个部分。前台对人界面友好，主要用于实时人工输入指令和观察仿真输出状态。后台将前台设置的具体变量值代入，进行具体的运算，将运算结果反馈到前台状态栏，绘制航迹曲线，并通过UDP网络端口将数据传输到其它分系统如VegaPrime三维视景仿真系统、GoogleEarth航迹地图绘制系统等进行互联仿真。

MATLAB GUI程序包含.m代码文件和.GUI界面文件。后台程序主要包含在.m文件中，算法流程图如图4所示。

图4 MATLAB GUI仿真代码流程图

首先进行外环航迹控制运算，获取系统输入的当前航路AB，通过定位装置获取船的位置P，求取垂点Q，根据Q点的位置不同进行分类讨论，求取目标点D。

其次进行中环航向控制运算，根据当前船位置P以及目标点位置D可以得到目标方向角θ，通过姿态检测装置获取船实时方向角α，可得到方向角偏差Δα，根据Δα值不同进行分类，求取实际偏转角r。

再次进行内环舵角控制运算，航向控制运算结果得到的偏转角r，与实际输出偏转角y进行比对，可以得到偏转角误差e(k)=r(k)-y(k)，根据前次e(k-1)以及此次e(k)可以得到微分值ec(k)=e(k)-e(k-1)，将e(k)与ec(k)进行模糊化，模糊整定得到ΔKp、ΔKi、ΔKd，计算Kp’、Ki’、Kd’计算PID控制器输出。

最后由PID控制器的输出作用在无人水面艇，使艇发生位置改变和方向角转动，跟踪目标航线。重复上述过程，重新进行下一轮的运算，则可以使无人水面艇持续进行航迹跟踪控制，直到抵达目的地。

3 仿真结果及分析

选取江苏省太湖水域作为航路规划的参考位置，选取水域的经度范围在123.324°E至120.344°E，纬度范围在31.437°N至31.447°N。规划航路中的各个航点的经纬度坐标如表1所示。

表1 航点经纬度坐标

3.1 舵角模糊PID控制仿真

舵角控制环系统输入为偏转角r=15°，PID控制器初始参数kp0=21，ki0=10，kd0=17，设定各参数模糊规则语句，控制器输出经过一阶滤波处理，无人水面船的传递函数为带有实参的二阶模型，仿真结果如图5所示。

图5 普通PID与模糊PID仿真结果对比

由于机械延迟，舵机在系统输入2 s后开始响应。普通PID仿真值在4.5 s达到最大值，而模糊PID仿真值在4 s达到最大值，两者超调均接近10%，在6 s左右系统趋于平缓无振荡。由此可见，模糊PID相比普通PID响应更为迅速，控制效果得到改善。

3.2 直线航迹跟踪控制仿真

选取表1规划航路的第五点(120.334°E，31.438°N)、第六点(120.340°E，31.440°N)组成当前直线航路，设定船的初始位置为(120.335°E，31.4375°N)，仿真结果如图6。

图6 直线航迹跟踪控制仿真

图示连续直线表示指定航路，点状曲线表示船的跟踪轨迹。船起始位置不在指定航路上，在航迹跟踪初始阶段船朝着指定航路靠近，一段时间后船行驶至指定航路并保持稳定行驶。

3.3 折线航迹跟踪控制仿真

选取表1规划航路的第五点(120.334°E，31.438°N)、第六点(120.340°E，31.440°N)与第七点(120.338°E，31.444°N)组成当前折线航路，设定船的初始位置为(120.335°E，31.4375°N)，仿真结果如图7。

图7 折线航迹跟踪控制仿真

船起始位置在指定航路外，初始阶段靠拢并行驶至第一条航路，当行驶中判断到拐点时，进行拐弯并行驶至下一航路。仿真曲线拐弯处的平滑度以及响应快慢与设定的触发距离以及航路拐角大小有关。

3.4 预定航路航迹跟踪控制仿真

依表1所示航路点绘制预定航路，船初始位置设定为(120.325°E，31.4375°N)，航迹跟踪曲线图如图8所示。

图8 预定航路航迹跟踪控制仿真

连续直线表示预定航路，点状曲线表示跟踪航迹。船从初始位置出发，首先完成“M”形折线航路行驶，再完成若干条直线航路行驶，在不同的直线航路之间包含角度各异的锐角和钝角，最后船完成环路航行，回到起点。由图可见，全程航迹跟踪没有发生航路偏离，直线行驶平稳，拐角转弯过渡自然。

4 结论

通过研究无人水面艇航迹跟踪控制方法，按照分层结构进行独立控制，仿真结果表明：

1)船航行过程中，内层舵角控制采取模糊PID控制器简洁有效，较短时间内达到预期控制目标，控制器参数具有自适应性，可靠性强；

2)外层航迹控制采取过渡目标点策略以及中层航向控制采取最小偏转角策略能够快捷的帮助无人船实现航行决策，直线行驶和折线行驶均能平滑稳定的实现航迹跟踪。

本次仿真基于Matlab GUI平台，理论计算结果可通过通信链路传输到其它仿真模块进行二次验证，也可以作为无人水面艇实际工程的测试依据，有助于无人水面艇实际航迹跟踪控制系统的实现。

[1] 董祖舜.快艇动力学[M].武汉:华中理工大学出版社,1991.

[2] 高 双.高速无人艇的建模与控制仿真[D].哈尔滨：哈尔滨工程大学,2007.

[3] 姚云熙.水面无人艇在风浪流干扰下的运动仿真[D].哈尔滨：哈尔滨工程大学,2007.

[4] 吴恭兴.水面智能高速无人艇的控制与仿真[D].哈尔滨：哈尔滨工程大学,2008.

[5] Caccia M, Bibuli M, Bono R, et al. Basic navigation, guidance and control of an unmanned surface vehicle[J]. Autonomous Robots, 2008, 25(4): 349-365.

[6] Bibuli M, Bruzzone G, Caccia M, et al. Path-following algorithms and experiments for an unmanned surface vehicle[J]. Journal of Field Robotics, 2009, 8(26): 669-688.

[7] 吴恭兴,邹 劲,孙寒冰,等.高速无人艇的运动建模及其视景仿真[J].大连海事大学学报,2010(1)：9-13.

[8] 王国英.欠驱动水面艇运动控制建模及三维仿真实现研究[D].哈尔滨：哈尔滨工程大学,2011.

[9] 隋晓丽.水面无人艇航迹控制算法研究[D].大连：大连海事大学,2013.

[10] 耿以才,黄立新,陈凌珊,等.无人船安全目标追踪与自动避障算法[J].计算机测量与控制,2015,23(7):2467-2469.

Simulation of Path Tracking Control of Unmanned Surface Vessel

Zhang Chen1, Liu Shou2, Li Baoan1,3

(1.School of Automation Science and Electrical Engineering, Beihang University, Beijing 100191, China;2.Beijing Aerospace Measurement and Control Technology Co., Ltd, Beijing 100041, China;3.Unmanned Aerial Vehicle Design Institute, Beihang University, Beijing 100191, China)

In order to improve the autonomous navigation ability of Unmanned Surface Vessel (USV) and reduce path error and track delay of path tracking, this paper proposes a hierarchical control structure for the trajectory tracking of unmanned surface vehicle under external wind, wave and current disturbances with model parameters uncertainly. The structure can be divided into three layers from outside to inside. Outermost layer of track control takes transition destination strategy to determine the real-time target position by the cross track distance. Intermediate layer of direction control takes minimum rotation angle strategy to determine the deflection angle by the difference between the heading angle and the given path angle. Innermost layer of rudder angle control designs a fuzzy PID controller to compensate the dynamic changes of model parameters. Under the MATLAB GUI environment a simulation was completed and the results indicate that the fuzzy PID controller increases the response speed of the rudder angle control and the USV have a good path tracking control in linear driving as well as nonlinear driving.

unmanned surface vessel; path tracking control; hierarchical control structure; fuzzy PID

2015-09-25；

2015-10-26。

张 臣(1990-)，男，湖北荆州人，硕士研究生，主要从事无人器建模与控制方向的研究。

1671-4598(2016)03-0088-04

10.16526/j.cnki.11-4762/tp.2016.03.024

TP242.6

A