基于Matlab仿真的数据降维实验设计

张文盛, 刘忠宝

(1. 山西大学商务学院 信息中心, 山西 太原　030031；2. 中北大学 计算机与控制工程学院, 山西 太原　030051)



基于Matlab仿真的数据降维实验设计

张文盛1, 刘忠宝2

(1. 山西大学商务学院 信息中心, 山西 太原030031；2. 中北大学 计算机与控制工程学院, 山西 太原030051)

在Matlab的基础上,以3种经典的数据降维方法——主成分分析(PCA)、线性判别分析(LDA)和保局投影算法(LPP)为例,给出3种降维方法的最优化比较结果,对数据降维实验方法进行了探讨和设计。通过UCI标准数据集和ORL、Yale人脸数据集的比较实验表明:3种降维方法均能较好地完成降维任务,其中LPP和LDA数据降维方法效率较优,但在不同的实验条件下,表现略有不同。

数据降维； Matlab仿真； 主成分分析； 线性判别分析； 保局投影算法

随着互联网的飞速发展,产生了海量数据,如何从海量数据中挖掘有用知识成为一个热点问题。数据挖掘是从大量的数据中提取知识的处理过程,研究数据挖掘技术具有重要的现实意义。数据降维是数据挖掘的重点问题之一。数据降维指从高维数据获取一个能真实反映原始数据固有特性的低维表示[1]。本文以3种经典的数据降维方法——主成分分析(principal component analysis,PCA)[2]、线性判别分析(linear discriminant analysis,LDA)[3]和保局投影算法(locally preserving projections,LPP)[4]为例,对数据降维实验方法进行深入探讨。鉴于Matlab优良的数据处理能力及其在分析统计和图形绘制方面具的优势,笔者提出基于Matlab仿真的数据降维实验设计方法。学生在学习数据降维的基本理论后,利用Matlab实现上述3种降维算法,通过对标准UCI数据集和人脸数据集实验的深入分析,加深对数据降维知识的理解。

1　数据降维方法

假设x=(x1,x2,…,xN)T为由N个d维样本xi(i=1,2,…,N)组成的数据集,Ni(i=1,2,…,c)为各类样本数,其中c为类别数。

1.1主成分分析(PCA)

主成分分析的基本思想是通过对高维数据进行压缩,从而获得一组具有代表性的统计特征。主成分分析能够用较少的特征来描述原始数据,并且保证在降维的同时尽量保持数据的原始特征。本质上,主成分分析可以转化为计算数据矩阵x协方差的特征值和特征向量问题[5]。对数据矩阵x中的各行向量进行零均值处理后可得x的协方差矩阵:

(1)

对上式中C进行正交分解有

(2)

其中λ=diag(λ1,λ2,…,λN),λi(i=1,2,…,N)为C的特征值且按降序排列；V=[V1,V2,…,VN],Vi(i=1,2,…,N)为与特征值λi对应的特征向量,将其称为第i个主成分方向。

数据集x在前n个主成分方向上降维后的信息保留率θ为

(3)

在实际应用中,一般取θ>0.85。

1.2线性判别分析(LDA)

线性判别分析保证样本在其找到的降维方向上具有较好的可分度,即同类样本尽可能紧密,而异类样本尽可能远离[6]。上述思想可由如下优化问题表示:

(4)

其中,WLDA为线性判别分析找到的降维方向,SB是类间离散度,表示异类样本之间的距离；SW是类内离散度,表示同类样本之间的距离。SB和SW的定义如下:

(5)

(6)

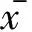
1.3保局投影算法(LPP)

保局投影算法的基本思想是保持高维数据在降维过程中相对关系不变，该思想可由如下最优化问题表示:

(7)

(8)

其中WLPP为降维方向,Dii=∑jSij,权重函数Sij用来表征样本之间的相似度,其定义如下:

(9)

其中t为常数。

上述最优化问题经代数变换可得如下形式:

(10)

(11)

其中L=D-S。

保局投影算法的降维方向WLPP可由方程XLXTWLPP=λXDXTWLPP的特征向量得到。

2　实验设计

实验的软硬件环境是IntelCorei3CPU,4GRAM,Windows7和Matlab7.0。实验的基本步骤如下:

(1) 将实验数据集按照一定比例划分为训练数据集和测试数据集；

(2) 在训练数据集上分别运行PCA、LPP、LDA等降维方法,得到相应的降维方向WPCA、WLPP、WLDA；

(3) 将测试数据集中的样本依次投影到降维方向WPCA、WLPP、WLDA上；

(4) 将降维后的测试样本通过支持向量机(supportvectormachine,SVM)与训练样本进行比较,得到识别结果。

2.1UCI数据集上的实验

选取UCI标准数据集中的Wine数据集[9],该数据集中样本数为178,类别数为3,维度为13。在上述数据集上分别运行PCA、LPP、LDA等降维方法,降维数为2,支持向量机算法的参数为

实验结果如图1所示,其中class1、class2、class3分别表示3类样本。

由图1可以看出:通过PCA降维后的3类样本重叠率较高,而且数据分布很不规律,降维效率较低；LPP和LDA均能较好地完成降维,但两者表现略有不同。通过LPP降维后的样本分布较为松散,并在各类边界有一定的重叠,但基本上能将3类样本分开；通过LDA降维后的样本分布紧凑,特别是3类样本没有重叠,与PCA和LPP相比,LDA降维能力较优。这是因为LDA在降维时保证同类样本距离尽可能近,而异类样本尽可能远,因此,通过LDA降维后的样本具有良好的可分性。

图1　UCI数据集上的实验结果

2.2人脸数据集上的实验

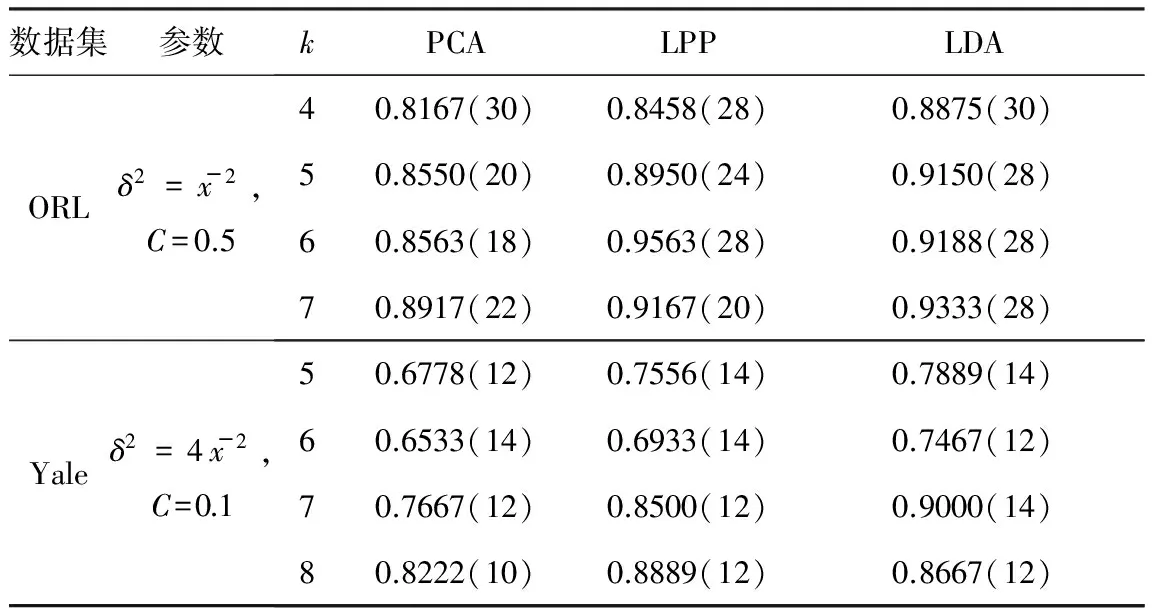
实验选取ORL人脸数据集和Yale人脸数据集,其中ORL人脸数据集包括40个人、每人10幅图像、共400幅图像,Yale人脸数据集包括15个人的165幅图像。上述人脸数据集的部分人脸图像如图2所示。实验分别选取ORL人脸数据集每人前m(m=4,5,6,7)幅图像以及Yale人脸数据集每人前n(n=5,6,7,8)幅图像为训练数据集,剩余样本用作测试。支持向量机的实验参数和在ORL、Yale数据集上分别运行PCA、LPP、LDA等降维方法,得到的实验结果如表1所示。

图2　人脸数据集部分人脸图像

数据集参数kPCALPPLDAORLδ2=x-2，C=0．540．8167(30)0．8458(28)0．8875(30)50．8550(20)0．8950(24)0．9150(28)60．8563(18)0．9563(28)0．9188(28)70．8917(22)0．9167(20)0．9333(28)Yaleδ2=4x-2，C=0．150．6778(12)0．7556(14)0．7889(14)60．6533(14)0．6933(14)0．7467(12)70．7667(12)0．8500(12)0．9000(14)80．8222(10)0．8889(12)0．8667(12)

注:括号外的值表示算法的识别率,括号内的值表示取得相应识别率时的维数。

由表1可以看出:与PCA和LPP相比,LDA在大多数情况下均能得到最优的降维效率。当训练样本选取ORL人脸数据集每人前m(m=4,5,7)幅图像以及Yale人脸数据集每人前n(n=5,6,7)幅图像为训练数据集时,LDA具有最优的降维效率；当训练样本选取ORL人脸数据集每人前6幅图像以及Yale人脸数据集每人前8幅图像为训练数据集时,LPP的降维效率最优,LDA次之,但两者相差不大。PCA在上述ORL和Yale人脸数据集上基本能完成降维,但降维效率较LPP和LDA低。

2.3进一步的实验

另外,LDA和LPP分别基于样本的全局特征和局部特征进行降维。需要研究一种兼顾样本的全局特征和局部特征的新的降维方法,以进一步提高降维效率。

3　结语

本文在Matlab的基础上,对PCA、LDA、LPP数据降维方法进行了实验研究。通过UCI标准数据集以及人脸数据集的降维实验表明,LPP和LDA数据降维方法效率较优,但在不同的实验条件下表现略有不同。该实验有助于学生深入理解数据降维的基本理论,为后续分类和聚类方法的学习奠定基础。

References)

[1] 刘忠宝.基于核的降维和分类方法及其应用研究[D].无锡:江南大学,2012.

[2] Du M J,Ding S F,Jia H J. Study on density peaks clustering based on k-nearest neighbors and principal component analysis[J].Knowledge-Based Systems,2016,99:135-145.

[3] Belhumeur P N, Hespanha J P, Kriegman D J. Eigenfaces vs. Fisherfaces:recognition Using Class Specific Linear Projection[J].IEEE Trans on Pattern Analysis and Machine Intelligence,1997,19(7):711-720.

[4] He X F,Niyogi P. Locality Preserving Projections[C]//Advances in Neural Information Processing Systems (NIPS).Vancouver,2003:153-160.

[5] Nobi A,Lee J W. State and group dynamics of world stock market by principal component analysis[J].Physica A:Statistical Mechanics and its Applications,2016,450:85-94.

[6] 王明合,张二华,唐振民,等.基于Fisher线性判别分析的语音信号端点检测方法[J].电子与信息学报,2015,37(6):1343-1349.

[7] Zhao Y,Wang K. Fast cross validation for regularized extreme learning machine[J].Journal of Systems Engineering and Electronics,2014,25(5):895-900.

[8] 郭美丽,覃锡忠,贾振红,等.基于改进的网格搜索SVR的话务预测模型[J].计算机工程与科学,2014,36(4):707-712.

[9] University of California Irvine. UCI Machine Learning Repository[EB/OL].http://archive. ics.uci.edu/ml/datasets/Wine.

[10] Alibeigi M,Hashemi S,Hamzeh A. DBFS:an effective density based feature selection scheme for small sample size and high dimensional imbalanced data sets[J].Data & Knowledge Engineering,2012,81/82(4):67-103.

Design of dimension reduction experiments based on Matlab simulation

Zhang Wensheng1, Liu Zhongbao2

(1. Information Center,Business College of Shanxi University,Taiyuan 030031,China;2. School of Computer and Control Engineering,North University of China,Taiyuan 030051,China)

The dimension reduction experiments based on Matlab simulation are designed. The performances of several traditional dimension reduction methods such as the principal component analysis (PCA), the linear discriminant analysis (LDA), the locally preserving projection (LPP) algorithm are compared in the standard datasets,and it can be concluded that the above methods can complete the dimension reduction task while their performances are slightly different from each other in different cases.

dimension reduction; Matlab simulation; principal component analysis (PCA); linear discriminant analysis (LDA); locally preserving projection(LPP)algorithm

10.16791/j.cnki.sjg.2016.09.030

2016-03-31

山西省高等学校科技创新项目(2014142)

张文盛(1974—),男,山西曲沃,硕士,实验师,主要研究领域为实验室信息化建设

E-mail：hello811120@sina.com

刘忠宝(1981—),男,山西太谷,博士,副教授,主要研究领域为智能信息处理.

E-mail：liu_zhongbao@hotmail.com

TP391

A

1002-4956(2016)9-0119-03