基于多重检验层次分析法的吸烟者戒烟影响因素研究

葛福婷　张秀　王家豪　朱家明*

(1. 安徽财经大学　统计与应用数学学院，安徽蚌埠　233030；2. 安徽财经大学　金融学院，安徽蚌埠　233030)



基于多重检验层次分析法的吸烟者戒烟影响因素研究

葛福婷1张秀1王家豪2朱家明1*

(1. 安徽财经大学统计与应用数学学院，安徽蚌埠233030；2. 安徽财经大学金融学院，安徽蚌埠233030)

针对吸烟者的戒烟意愿及戒烟成功的影响因素研究，运用MATLAB、SPSS、STATA等软件编程，分别构建频率分布、独立性检验和层次分析模型，得到吸烟者的戒烟意愿(分不同年龄、性别等讨论)，各因素影响下再吸烟者的累加发病率分布状况，CO浓度、距离抽最后一只烟的分钟数、每日抽烟只数为影响戒烟成功的主要因素等结论，从而对吸烟者采取有针对性的措施促进戒烟。

戒烟；独立性检验；层次分析法；White异方差检验；RESET检验；MATLAB；STATA；SPSS

众所周知，吸烟不仅有害自身健康，还会引起被动吸烟，危害公众身心健康。为此，如何帮助相关人士摆脱烟瘾的困扰成为一个重要的研究课题。笔者试图通过参与调查的234位吸烟者1年内的各种戒烟数据，探讨影响吸烟的戒烟意愿以及影响戒烟成功的影响因素，为发现有效的戒烟策略和方法提供理论依据[1]，有针对性地高效地促进吸烟者戒烟。

1　数据的获取和假设

数据源于2015年安徽财经大学数学建模暑期第一次模拟B题中234位参与调查的烟民1年间的相关统计数据[2]。为便于解决问题，提出如下假设：1)所研究的6个戒烟因素(性别、年龄、每日抽烟数、CO浓度、距离抽最后一支烟的分钟数和调整后CO浓度)对戒烟成功者毫无影响；2)戒烟天数除研究给出的6个因素外，不受其它因素的影响；3)所给的数据真实、可靠；4) 原烟民戒烟的可信度是很低的(即再犯者)，戒烟天数是是从0到他(她)退出戒烟或研究截止时间(1 年)的天数；5)参与戒烟研究的烟民中途均未退出；6)由于存在个别极端数据不合实际情况，所以存在人为修改的数据，修改幅度较小。

2　再吸烟者累加发病率分布状况分析

2.1研究思路

研究234名吸烟者中再次吸烟的累加发病率[指戒烟失败人数(即少于一年戒烟天数的人数)与总调查人数的比值]分布情况。首先，通过直观判断，发现存在数据的部分缺失，为了保证研究数据的完整性和可靠性，运用SPSS软件弥补缺失值；其次，根据定义，得到总体再抽烟的累加发病率状况，侧面反映戒烟率；再次，对研究的6大影响因素分阶段分析各影响因素下的累加发病率分布状况；最后，综合上述分析，直观全面的得到各因素下吸烟者再吸烟的累加发病率分布状况、戒烟率，得到初步规律，为下文定量研究影响戒烟成功的主要因素提供理论基础。

2.2研究方法

1)可能影响戒烟的因素。

根据已有研究数据，确定影响戒烟可能存在的6种因素：性别、年龄、每日抽烟数、CO浓度、距离抽最后一支烟的分钟数和调整后CO浓度(为研究方便，该文仅研究此6种因素)。

2)弥补缺失值。

将研究数据全部导入SPSS[3]软件，编辑易知所给数据缺失率为0.044 6，缺失率较小，故SPSS软件就可以满足数据的可靠填充，可使用“线性趋势法”进行补充[4]。鉴于数据过多，这里不赘述。

3)累加发病率分布。

(1)

根据公式(1)，进一步统计得总体戒烟的累计发病率，见表1。

表1　总体再抽烟的累加发病率状况

由表1可知，总体再抽烟的累加发病率为85.90%，即绝大多数戒烟人士人很难坚持365 d，但具体何种因素、如何具体来影响累加发病率，仍需要进一步研究。基于频率分布模型[5]，下面通过不同性别、年龄、每日抽烟数、CO浓度、距离抽最后一支烟的分钟数和调整后CO浓度情况下对累加发病率进行比较和分析。

①性别。

根据不同性别对吸烟者再抽烟的累加发病率影响进行统计，结果见表2。

表2　不同性别影响下累加发病率分布表

由表2可知，不同性别对再次吸烟的累加发病率的影响差别不是很大。男性的累加发病率为84.55%，而女性的累加发病率87.10%，总体来说女性的发病率略高于男性2.55%。换而言之，男性的戒烟率为15.45%，女性为12.90%。

②年龄。

通过对数据分析，易知调查对象的年龄跨度为21～76岁，结合联合国的世界卫生组织(WHO)的年龄划分规定及研究数据，将调查对象的年龄划分为4个阶段(鉴于调查对象年龄跨度的限制，对少年人和老年人的研究存在缺失及偏误)：青年人(20～44岁)，中年人(45～59岁)，年轻老年人(60～74岁)，老年人(75～76岁)，统计可得不同年龄阶段再次发病时的累加发病率分布状况，见表3。

表3　不同年龄影响下累加发病率分布表

由表3知，剔除仅1个样本量的老年人组(75～76岁)后，45～59岁的中年人的发病率最高，高达88.89%；其次是20～44岁的青年人，发病率达到86.43%；最低的是年龄段60～80岁的老年人，虽然最低但也高达71.43%。总的而言，抽烟的发病率都偏高，中年人戒烟难度最大，这与自身的约束力及累计烟龄有很大的关联。

③每日抽烟数。

通过对数据分析，易知每日抽烟数的数量跨度为2～90支，人为地将每日抽烟数划分为5个阶段：0～20、21～40、41～60、61～80、81～100，分别求出各阶段下的累加发病率，结果见表4。

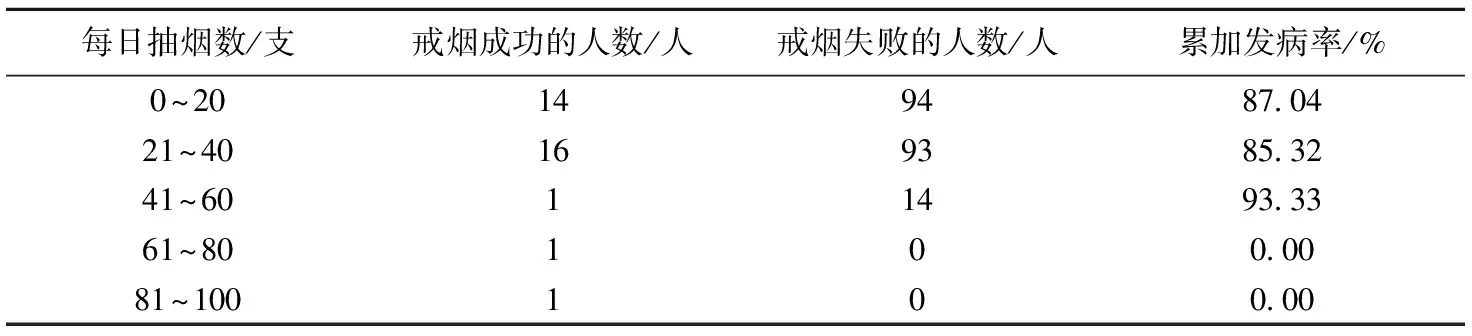
表4　不同每日抽烟数影响下累加发病率分布表

由表4知，每日抽烟数为41～60的调查人群再抽烟的累加发病率最高，高达93.33%；其次是每日抽烟数为0～20及21～40的调查人群，再抽烟的累加发病率达到87.04%、85.32%；每次抽烟人数为61～80及81～100的调查人群再抽烟的累加发病率最低，近似为0。综合而言，每日抽烟数在60支以上的人在少数具有偶然性，在分析时可适当忽略，剔除这种状况，每日抽烟数与累加发病率成正比。

④CO浓度。

通过对数据的分析，并结合EXCEL作出CO浓度与戒烟天数的散点图分析，CO的浓度跨度为40～990，将CO浓度划分为5个阶段：0～200、201～400、401～600、601～800、801～1 000。再计算出各阶段CO浓度下的累计发病率，见表5。

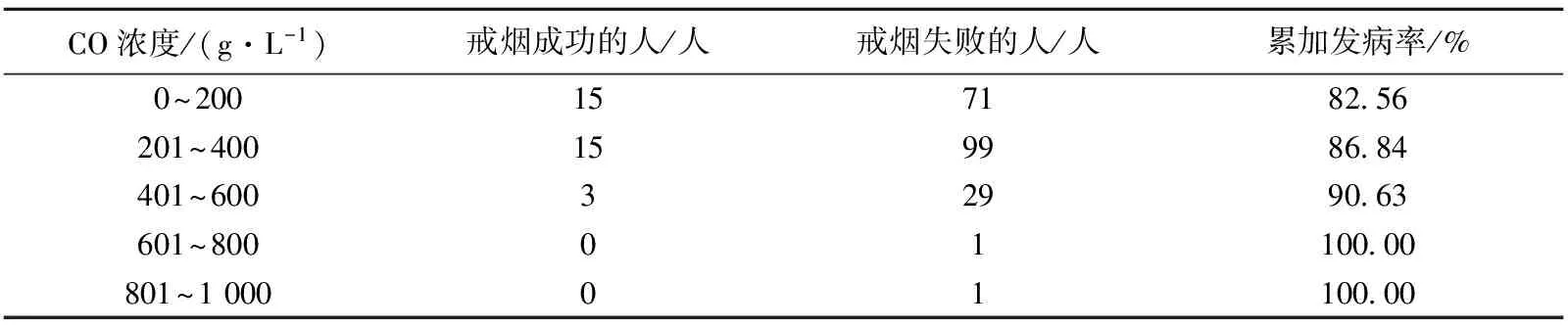
表5　不同CO浓度影响下累加发病率分布表

由表5易知，调查人群中再抽烟的累加发病率是随着CO浓度(即吸烟多年累计的CO浓度，反应为吸烟患者的烟龄和吸烟总量)的增加而递增的，总体呈现较高的累加发病率，当CO浓度达到600以上时吸烟者必然会再次吸烟。

⑤距离抽最后一支烟的分钟数。

根据已有相关数据，作出距离抽最后一支烟的分钟数与戒烟天数的散点图，如图1所示。可知距离抽最后一支烟的分钟数对累加发病率的影响并没有很强趋势的关系，即它对调查对象再抽烟的累加发病率分布没有形象化的规律。

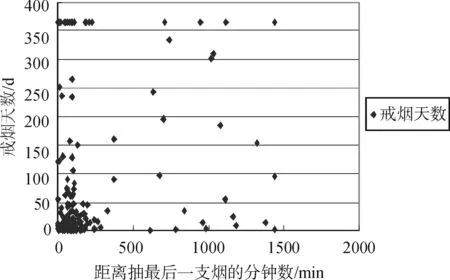
图1　距离抽最后一支烟的分钟数与戒烟天数散点图

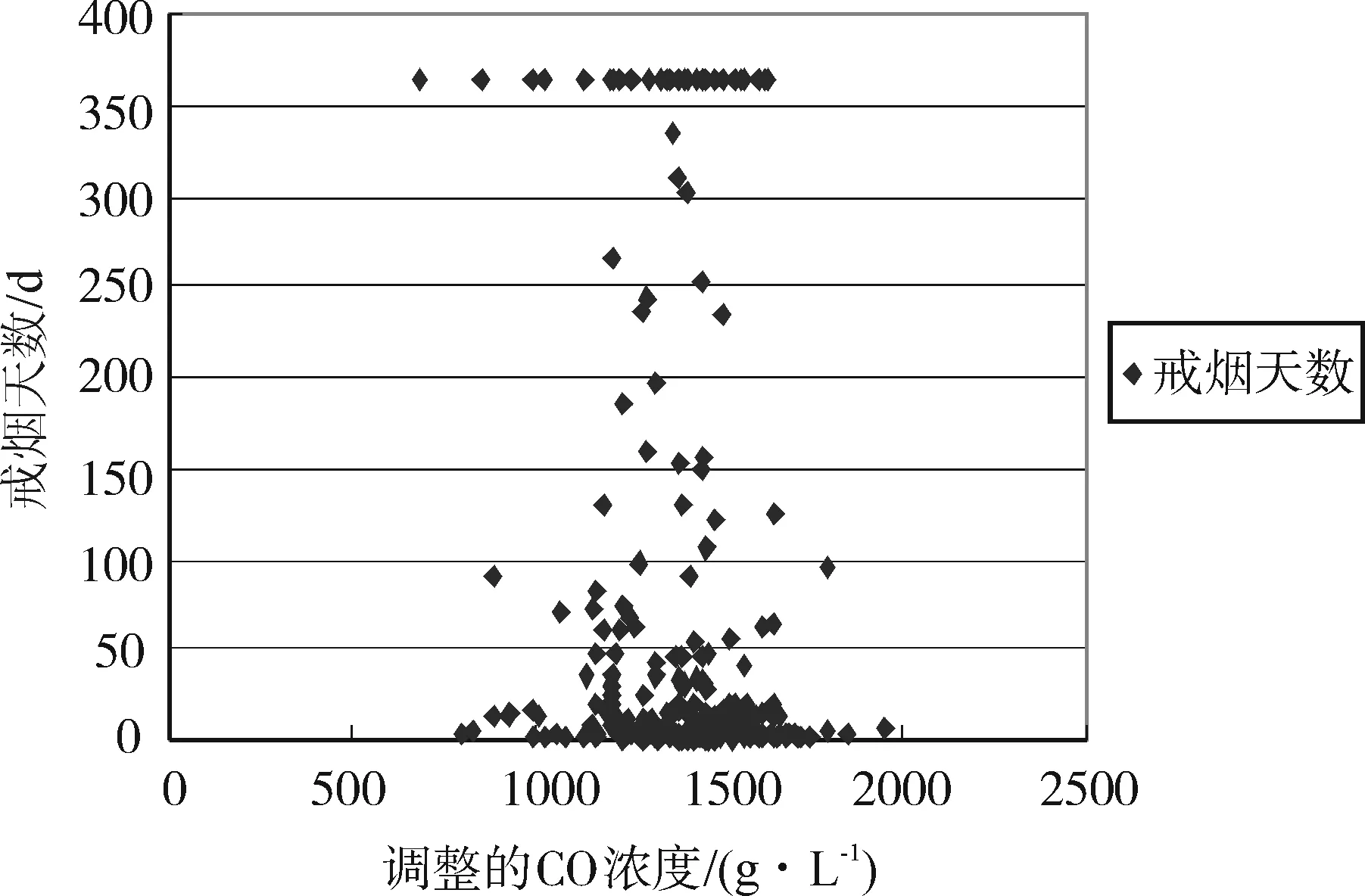
图2　调整的CO浓度与戒烟天数散点图

⑥调整的CO浓度因素的影响。

作出调整的CO浓度与戒烟天数的散点图，如图2所示。由此可知不同的CO浓度下戒烟天数分布的相对有一定的规律，人为将调整的CO浓度分为6个阶段：0～1 150、1 151～1 300、1 301～1 450、1 451～1 600、1 601～1 750、1 751～2 000。计算出不同阶段调整的CO浓度下再吸烟者的累加发病率，见表6。

表6　不同调整CO浓度影响下累加发病率分布表

由上述结果可知，再抽烟的累加发病率随着调整后的CO浓度的升高而增加，累加发病率偏高。

2.3结果分析

综上分析可知，总体上吸烟患者再吸烟的累加发病率是偏高，达85.90%，也即被调查者中85.90%的吸烟患者戒烟是不成功的，戒烟率为14.1%。概括其它6种影响因素下的累加发病率分布：吸烟患者再吸烟的概率偏高，达80%以上，女性患者较男性发病率略偏高，男性患者和女性患者的戒烟率分别为15.45%和12.90%；45～59岁的中年人的发病率最高，高达88.89%；剔除每日抽烟数在60支以上的少数患者，每日抽烟数与累加发病率成正比；一定范围内，累加发病率同CO浓度和调整后的CO浓度成正比；此外，累加发病率同距离抽最后一支烟的分钟数并无明显的规律性关系。上述结论将为进一步研究影响戒烟成功的主要影响因素提供理论支持。

3　影响戒烟成功的主要影响因素分析

3.1研究思路

要研究的是判断年龄、性别、每日抽烟支数及调整的CO浓度等因素对戒烟时间长短的影响，并对可能影响戒烟时间长短的因素进行定量分析[6]。首先，对可能影响再抽烟的累加发病率的因素进行编号，并用MATLAB对各因素对累加发病率的显著性作初始化的数据处理，得出各因素对戒烟时间有无显著性影响的初始结论；其次，依据上述结果，就影响戒烟时间长短的各因素作进一步的数据分析，拟合出趋势图[7]并量化表示戒烟时间与各影响因素间的关系。最后，归纳总结影响戒烟时间长短的各因素与戒烟时间的关系，以给出定量化的表达。

3.2研究方法

1)数据初始化处理。

对可能影响戒烟时间长短的因素编号：年龄X1、性别X2、每日抽烟支数X3、CO浓度X4、距离抽最后一支烟分钟数X5及调整的CO浓度X6，戒烟天数为Y。基于大样本数据(N= 234 > 30)的Z检验法，对各因素与戒烟时间的相关性与显著性进行检验，运用MATLAB编程[8]，整理结果见表7。

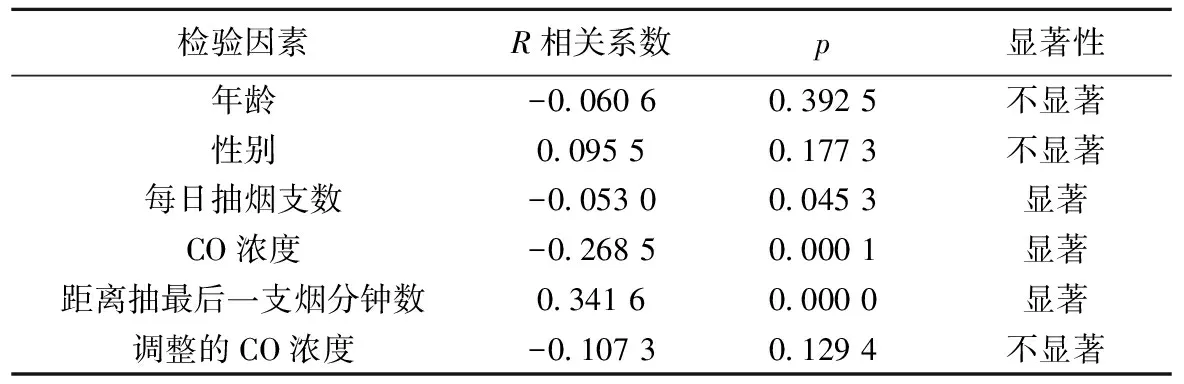
表7　各因素与戒烟时间的相关性及显著性检验

表7中，在5%的显著性水平下，年龄、性别和调整的CO浓度与戒烟时间无关，而每日抽烟只数、CO浓度以及距离抽最后一支烟分钟数对戒烟时间显著相关。但在多变量数据的相关性和回归性分析的情况下，仅由p<0.05来判断结果无效而被拒绝接受的水平的选择具有武断性。故为了更真实的反映戒烟时间是否与各因素存在关系，对各因素作进一步的分析判断。

2)戒烟时间与可能的影响因素定量分析。

通过简单的判断，戒烟时间为365 d的调查对象戒烟成功[9]，对相应的各因素不存在影响，故剔除掉戒烟时间为365 d对应的极端数据，进一步做定量分析。

①年龄因素的影响。

首先用EXCEL做出戒烟天数与年龄Y-X1的回归曲线，如图3所示，依据散点图，再运用STATA软件(后面各因素拟合处理方法类似)，多重函数迭代拟合得最优的回归函数(这里的最优是指软件本身可拟合的最好结果(R2>0.8)，不同函数形式可能拟合优度的高度差不多，结果不唯一)：

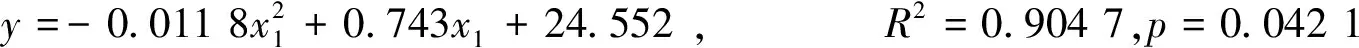
R2>0.9，可决系数较高，且在5%的显著性水平下，p=0.042 1<0.05,拒绝原假设：模型的建立是不合理的，即Y-X1间的回归函数是可靠的。

②性别因素的影响。

同理作出戒烟天数与性别的散点图，如图4所示，女性戒烟天数普遍比男性偏高。

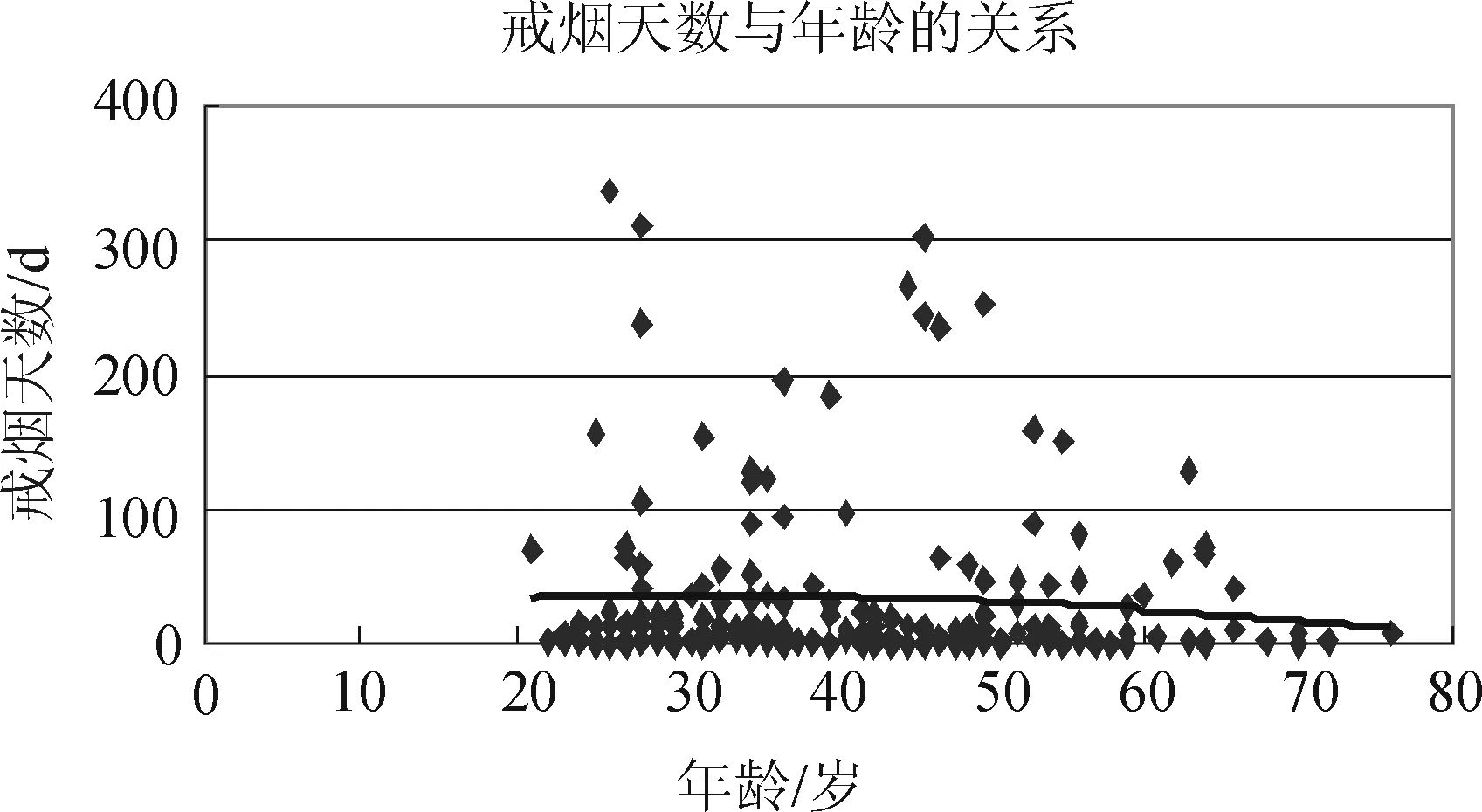
图3　戒烟天数与年龄关系图

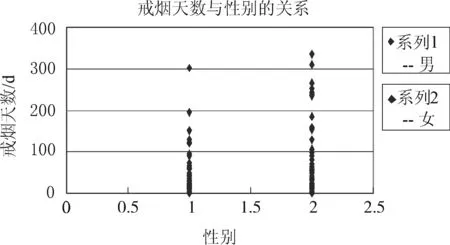
图4　戒烟天数与性别关系图

③每日抽烟支数因素的影响。

作出戒烟天数与每日抽烟支数的散点图，如图5所示。显然每日抽烟支数与戒烟天数关系不明显，通过Excel趋势得出的拟合曲线的可决系数R2较低，但在5%的显著性水平下拒绝原假设，所以每日抽烟支数与戒烟天数函数相对较合理(由于数据分布趋势性不强，拟合结果存在一定偏误)。

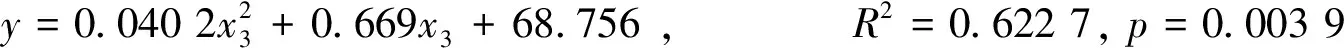
④CO浓度因素的影响。

作出戒烟天数与CO浓度关系的散点图并拟合曲线，如图6所示。从散点图走势和拟合曲线看出CO浓度越高，戒烟天数越低，存在相关性。

y=-30.388ln x4+197.59 ，R2=0.876 6， p=0.043 2 ，

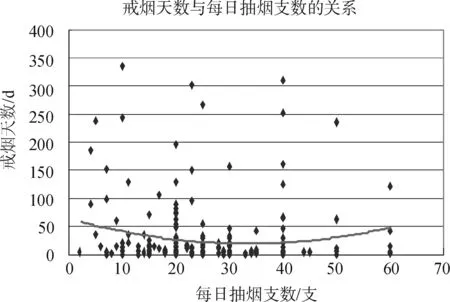
图5　戒烟天数与每日抽烟只数关系图

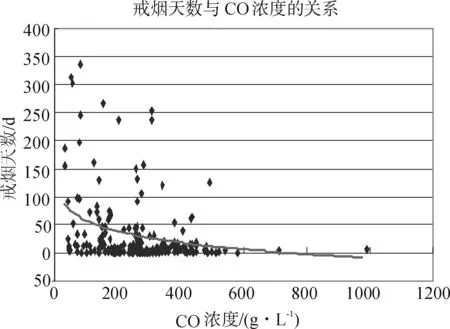
图6　戒烟天数与CO浓度关系图

⑤距离抽最后一支烟的分钟数因素的影响。

作出戒烟天数与距离抽最后一支烟的分钟数的散点图，如图7所示。

针对图7，通过拟合曲线看出大部分数据都聚集在0～200之间，并且趋势较直观，随着距离抽最后一支烟的分钟数的延长戒烟天数在增加，拟合函数如下：

y=10.729ln x5-13.858 ，R2=0.849 9， p=0.049 5 ，

易知函数拟合结果存在较强的相关性。

⑥调整的CO浓度因素的影响。

作出戒烟天数与调整CO浓度的散点图，如图8所示。多重迭代拟合后的最优拟合函数如下：

图7　戒烟天数与距离最后一支烟的分钟数关系图

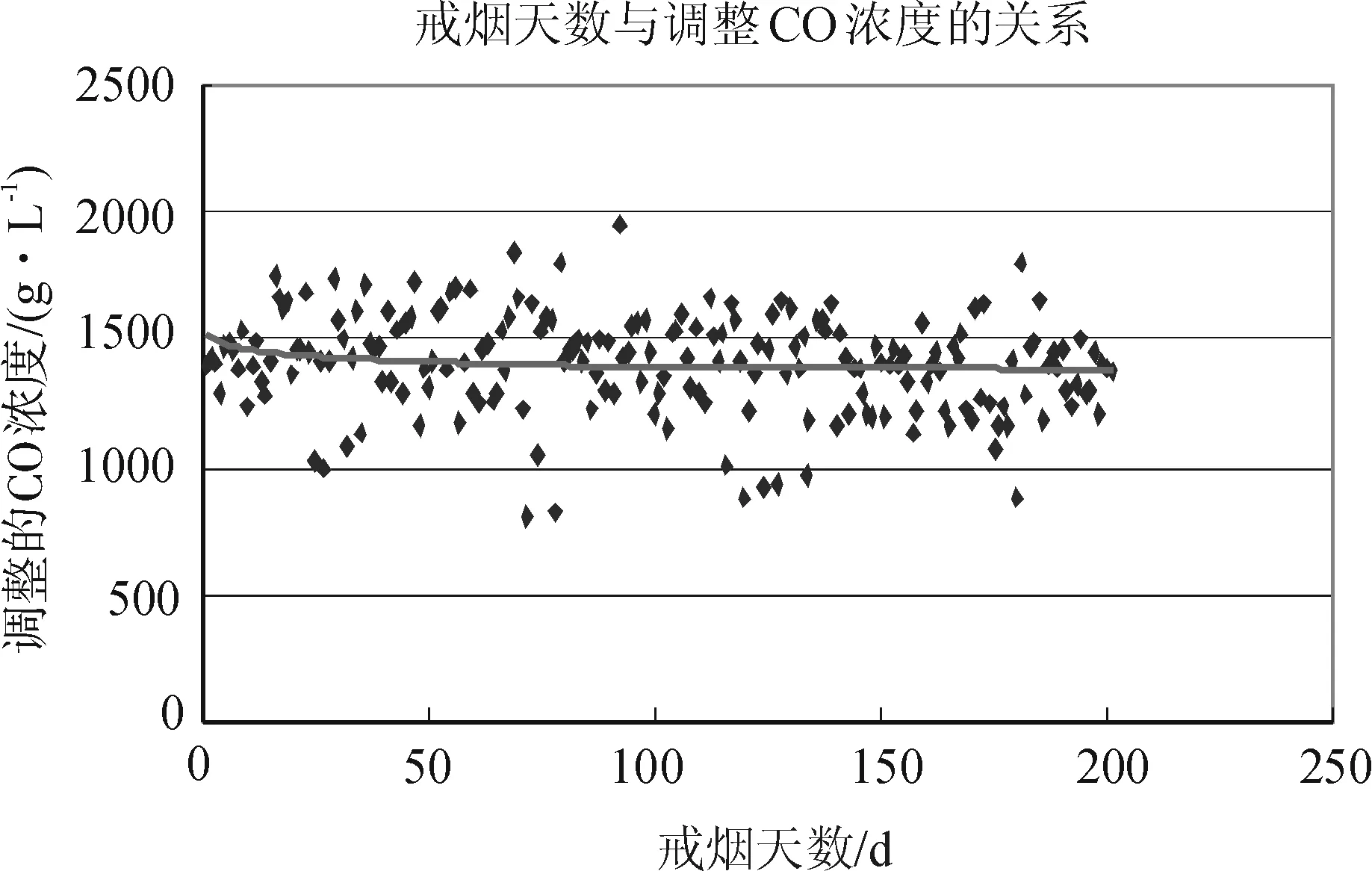
图8　戒烟天数与调整CO浓度关系图

拟合结果较佳，调整CO浓度越高戒烟天数越低，但是从拟合的曲线可知它们的关联较弱。

由此，宏观上了解到戒烟时间与各可能的影响因素间的关系，得到初步的结论，为更明确了解各因素影响大小，在(4)部分引入层次分析法[10]着重分析影响戒烟成功与否的主要因素。

3)模型的显著性检验。

为使拟合结果更有说服力，运用STATA软件，结合独立性检验的方法证明模型的合理性。对CO浓度对戒烟天数的影响的模型合理性详细阐释，其它各因素可类似处理，鉴于文章篇幅，不赘述。

I)White异方差检验。

原理[11]假设回归模型为：

Yi=β0+β1X1i+β2X2i+ui，

(2)

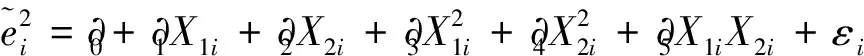
(3)

可以证明，在同方差性假设下，从该辅助回归得到的可决系数和R2与样本容量n的乘积，逐渐地服从自由度为辅助回归得到的解释变量个数的χ2分布：nR2～χ2。则在大样本(n>30,本文n=234)下，对统计量nR2进行相应的χ2检验。

辅助回归是为了检验与解释变量可能的组合的显著性，因此，辅助回归方程还可引入解释变量的更高次方。通过比较p值与给定的显著性水平的关系来判断是否与解释变量的某种组合有显著的相关性，当然，为了证明原定量模型的可靠性结果是不存在异方差的。

运用STATA软件编程，原始模型中戒烟时间y与CO浓度x的普通最小二乘法回归结果。

Source |SSdfMSNumber of obs = 234

Model |163209.102 1163209.102 Prob > F=0.0016

Residual |3712862.62 23216003.7182 R-squared =0.0421

Total |3876071.73 233 16635.501 Root MSE=126.51

y |Coef. Std. Err.tP>|t| [95% Conf. Interval]

lnx4 |-41.76158 13.07721-3.19 0.002-67.52686 -15.99631

_cons | 304.9826 70.94538 4.30 0.000 165.2031444.7622

原始模型进行普通最小二乘回归得到的残差平方项的辅助回归结果：

Source | SS df MSNumber of obs = 234

Model |2.4023e+09 21.2012e+09 Prob > F=0.1884

Residual |1.6502e+11 231 714359897 R-squared =0.0143

Total |1.6742e+11 233 718538435 Root MSE= 26728

e2 |Coef. Std. Err.tP>|t| [95% Conf. Interval]

lnx4 | 18853.05 35482.13 0.53 0.596-51056.9388763.02

lnx4sq |-2309.165 3465.161-0.67 0.506-9136.5264518.196

_cons |-17752.69 89874.43-0.20 0.844-194831.1159325.7

最后的p值输出结果：Chi2 =3.357 690 3 ,Prob=0.006 589 34。

在1%的显著性水平下，p<0.01，拒绝原假设：模型的误差项存在异方差。说明残差平方和与解释变量不存在显著的相关性，也证明了原模型变量的设置是可靠的。

II)RESET检验。

基于上述White异方差检验不存在异方差的理论基础，进一步地检验在给定的显著性水平下，模型是否存在设定误差[12]。运用STATA编程，运行结果如下：

Ramsey RESET test using powers of the fitted values of y

Ho:model has no omitted variables

F(3, 229)=0.42

Prob>F=0.005 6

在1%的显著性水平下，p=0.005 6<0.01，拒绝原假设：模型存在设定误差，即在给定的显著性水平下，模型不存在设定误差。

综合White异方差检验和RESET检验的结论，证明了原模型建立的可靠性。

4)影响戒烟成功的主要影响因素分析。

I)确定比较判断矩阵。

根据上述的层次关系，若计算出方案层对目标层的权重关系首先必须明确准则的比较判断矩阵。

通过查阅资料，得到专家认定影响戒烟成功与否的内、外在因素的比较判断矩阵如下：

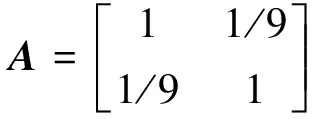
即内外在因素之比为0.1 ∶0.9，内在因素指年龄、性别，外在因素指每日抽烟支数、CO浓度、距离抽最后一支烟分钟数及调整的CO浓度。

II)确定各因素权重。

用变异系数法分别求得内、外在因素各因素权重，具体求法如下：

(4)

其中i=1,2,…,6，分别表示年龄、性别、每日抽烟支数、CO浓度、距离抽最后一支烟分钟数及调整的CO浓度六大因素，j=1,2,…,234分别表示各因素下的234个样本数据。

(5)

(6)

(7)

Step5运用MATLAB软件编程，得各指标数值分布表，见表8。

表8　变异系数法下内、外在因素各指标数值

III)确定各因素综合影响权重。

建立六行两列的内外在因素权重矩阵，求解方案层相对于目标层的总排序向量：

3.3结果分析

由上述权重的大小的比较可以得到各指标对戒烟天数的影响有强到弱依次为：距离抽最后一支烟的分钟数，CO浓度，每日抽烟支数，性别，年龄，调整CO浓度，结合85%的主成分权重原则[13](即依据权重从高到低累计，直至累计权重恰好大于85%所确定的因素，即为影响方案层的主成分分数)，确定影响戒烟成功的主要因素为：距离抽最后一支烟的分钟数，CO浓度，每日抽烟支数(53.04% + 16.77% + 15.75% = 85.56% > 85%)，前两个因素客观的反应为烟龄长短和累计抽烟数量。

4　结语

对目前研究较少的戒烟影响因素进行分析，探究影响戒烟的危险因素及吸烟者的戒烟意愿，从而为发现有效的戒烟策略和方法提供理论依据。基于234名吸烟者参与为期1年的戒烟调查数据，使用SPSS、STATA、MATLAB等软件对数据分析，结果检验采用Z检验、White异方差检验和RESET检验，以层次分析法综合多因素分析，筛选得到影响戒烟成功的主要因素，并探究作用的大小。

此外，戒烟成功与否还与个人性格特征因素、受教育程度、职业、环境因素、经济条件等有相关的联系，但出于数据获取难度大和已有的相关研究[14]，进一步拓展研究无现实意义，故不赘述。

基于研究的结果，提出如下建议：在高达85.90%的戒烟率(即累加发病率)下，加强吸烟者的管理，特别针对每日吸烟数多、烟龄长的中年人群，有针对性地采取措施，努力促进更多的吸烟者戒烟。同时，如果对社会经济地位较低人群早期干预，在工作场所严格限烟、禁烟可以降低吸烟率；加强控烟工作包括医务人员的戒烟知识培训、社会媒体、社会和学校的健康教育，加强烟草危害的宣传，会促进吸烟者的戒烟意愿，并促成其戒烟。

[1]林沛茹,何雩霏,张颖,等.吸烟者戒烟的影响因素分析[J].实用医学杂志,2013,29(9):1467-1470.

[2]朱家明.2015年安徽财经大学暑期数学建模模拟题1[EB/OL]. (2015-08-21)[2016-05-02].http://zhujm1973.blog.163.com/blog/static/31551355201581832245781/.

[3]龚学臣.SPSS18.0在裂区试验结果方差分析中的应用[J].河北北方学院学报,2014,30(5):53-55.

[4]杨桂元,朱家明.数学建模竞赛优秀论文评析[M].合肥:中国科学技术大学出版社,2013:136-165.

[5]谢华,黄介生.两变量水文频率分布模型研究述评[J].水科学进展,2008,19(3):30-37.

[6]葛福婷,朱家明,张秀,等.基于结构方程的西北干旱地区生物多样性研究[J].兰州文理学院学报,2016,30(2):30-37.

[7]李霞,方海玲,张荣,李媛.基于DEA 方法的中国能源工业技术创新效率研究[J].河北北方学院学报,2015,31(2):49-52.

[8]李柏年,吴礼斌.MATLAB数据分析方法[M].北京:机械工程出版社,2014:123-124.

[9]褚成静,张岚,杨彦春.成年男性戒烟失败影响因素分析[J].中国公共卫生,2012,28(1):7-9.

[10]钱军程,饶克勤,高军，等.戒烟与复吸影响因素及戒烟者健康状况分析[J].中国卫生统计,2009,26(2):150-153.

[11]刘明.异方差White检验应用的几个问题[J].统计与信息论坛,2012,27(6):45-48.

[12]韩本三,曹征,黎实.二元选择面板模型的设定检验[J].统计研究,2012,29(7):82-85.

[13]杨桂元.数学建模[M].上海:上海财经大学出版社,2015.

[14]刘文燕.吸烟与戒烟意愿及其影响因素的研究[D].长沙:中南大学,2011.

Analytic Hierarchy Process with Multiple Test

GE Futing1ZHANG Xiu1WANG Jiahao2ZHU Jiaming1*

(1. School of Statistics and Applied Mathematics, Anhui University of Finance and Economics, Bengbu 23303, China;2. School of Finance， Anhui University of Finance and Economics, Bengbu 23303, China)

With a focus on will and influence factors of success in quitting smoking, this paper describes the construction of frequency distribution, independence test and analytic hierarchy process, comprehensively analyzing the quitting smoking will (different age, gender, etc are discussed), the accumulative incidence distribution of re-smokers, and main influences of the successfully quitting smoking factors including carbon monoxide concentration, distance number of minutes of the last cigarette, and number of daily smoking through the software of MATLAB, STATA and SPSS, so as to take targeted measures to promote for smokers to kick the habit.

quit smoking; independence test; analytic hierarchy process; white heteroscedasticity testing; RESET inspection; MATLAB; STATA; SPSS

2016-05-09

国家级创新训练项目(AH201610378298)。

葛福婷(1995—)，女，安徽舒城人，主要从事经济统计方面研究。

朱家明(1973—)，男，安徽泗县人，副教授，硕士，主要从事应用数学与数学建模方面研究。

R163；R193.2

A

1009-0312(2016)05-0014-09