一类分数阶差分方程边值问题多重正解的存在性

王金华，向红军（湘南学院数学与金融学院，湖南郴州423000）

一类分数阶差分方程边值问题多重正解的存在性

王金华，向红军
（湘南学院数学与金融学院，湖南郴州423000）

考虑一类高阶分数阶差分方程边值问题.构造相关的格林函数，利用不等式技巧，分析格林函数的特征性质.运用不动点指数理论，获得了该分数阶差分方程边值问题存在多重正解的充分条件，举例说明了所获理论的有效性.

多重正解；边值问题；分数阶差分方程；存在性

1　引言

分数阶微积分是整数阶微积分的扩展，且比整数阶微积分能更好地描述现实中的某些现象.因此，近十年来得到了较好的发展，涌现了大量的研究文献.特别是分数阶微分方程边值问题理论得到了较大丰富，见参考文献［1-3］及所引参考文献.而离散分数阶微积分研究较少，主要是研究相对困难，因而发展较为缓慢.近年来，分数阶差分方程的相关研究也取得了一些非常可喜的开拓和发展.一些先行者如国内学者程金发和国外学者Atici F M，Eloe P W等取得很多系统的研究成果，介绍了分数阶差分方程理论及研究方法，参见文献［4-7］.由此，分数阶差分方程边值问题的研究受到国内外学者的关注，并逐渐成为热点，目前仍是一个很新的研究领域，见文献［8-15］.目前大多数文献研究的阶数不超过2，所用方法比较多见的主要是压缩映射原理，Schaefer’s不动点定理，K rasnosel’skii不动点定理等.如文献［11］用K rasnosel’skii不动点定理讨论了分数阶差分(边值问题：

分别获得了该问题正解存在性及唯一性的充分条件.

文献［12］描述了分数阶差分与整数阶差分方程边值问题的不同之处，研究了分数阶差分边值问题：

作者用偏序空间中的不动点理论得到了该方程正解存在唯一的充分条件.

本文考虑更高阶的分数差分方程边值问题：

2　预备知识

先给出本文后面要用到的一些定义和引理.

定义2.1［8，12］定义对任意t和v右边有定义.如果t+1-v是Gamma函数的极点，而t+1不是Gamm a函数的极点，则tv=0.

定义2.2［8，12］对v＞0，函数f的v阶分数和定义为

定义

α为实数，a，b为整数.

对v＞0，f的v阶分数差分定义为Δvf（t）：=ΔNΔv-Nf（t），t∈Na+N-v且N∈N满足0≤N-1＜v≤N.

引理2.1［8，12］假设N∈N，0≤N-1＜v≤N，则

引理2.2［14］设a∈R，v＞0.则Δ（t-a）v=v（t-a）v-1，对任意t两边有定义.此外，对n-1＜v≤n，n∈N1及µ∈R（-N1），

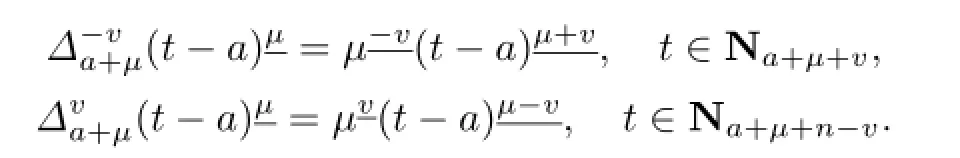
注1由引理2.2和Gamm a函数的基本性质，易得：

引理2.3［13］设Y是一个Banach空间，K⊆Y是Y内的一个锥.对q＞0，定义Kq=｛x∈K；‖x‖≤q｝.若Q：Kq→K是一个紧映射，使得当x∈∂Kq=｛x∈K，‖x‖=q｝时，有Qx/=x，那么（1）当x∈∂Kq时，若‖x‖≤‖Qx‖，则i（Q，Kq，K）=0；（2）当x∈∂Kq时，若‖x‖≥‖Qx‖，则i（Q，Kq，K）=1.

3　格林函数及其性质

为了简化主要结果的证明，先讨论与方程（1.1）相关的格林函数，并证明所得的格林函数的一些重要性质.

引理3.2 Green函数G（t，s）有如下性质：

当t=v+b时，

证由引理3.2的（2）-（4）可知：

4　解的多重性

本节用不动点指数理论证明分数阶差分边值问题（1.1）多重正解的存在性.

由引理3.1知，y（t）为边值问题（1.1）的解当且仅当满足y=Ty，y∈Y.

下面给出证明本节结论所需要的条件：

引理4.1 T是完全连续映射，且T（K）⊂K.

显然，由（H1）知T是完全连续映射.下面证明T（K）⊂K.

由引理3.3，对任意y∈K有，

即Ty∈K.

定理4.1设函数f（t，y）满足（H1）-（H3），则边值问题（1.1）至少存在两个正解y1，y2满足

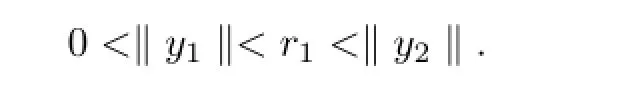
证取一个正数ξ＞0，使

由（H3）存在正数µ1，0＜µ1＜r1，使得f（t，y）≥ξy，对任意的0≤y≤µ1，t∈Nv+bv-3成立，因此，对y∈∂Kµ，有

即当y∈∂Kµ1时，‖Ty‖＞‖y‖.由引理2.3，有

即当y∈∂K时，‖Ty‖＞‖y‖.因此

另一方面，由（H2），对任意y∈∂Kr1有，

因此，当y∈∂Kr1时，‖Ty‖＜‖y‖.显然，当y∈∂Kr1时，Ty/=y，所以

综合（4.1）-（4.3），可得：

所以，T有两个不动点y1，y2，分别属于即边值问题（1.1）有两个正解y1，y2满足

定理4.2设函数f（t，y）满足（H1），（H4），（H5），则边值问题（1.1）至少存在两个正解y3，y4，满足：0＜‖y3‖＜r2＜‖y4‖.

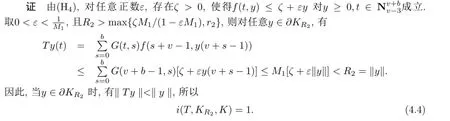
类似地，对0＜µ2＜r2，有i（T，Kµ2，K）=1.

另一方面，对任意y∈∂Kr2，有且由（H5）可得：

因此，当y∈∂Kr2时，有‖Ty‖＞‖y‖.显然，当y∈∂Kr2时，Ty/=y，所以

因此类似于定理4.1的证明，可得分数阶差分边值问题（1.1）至少有两个正解y3及y4，满足：

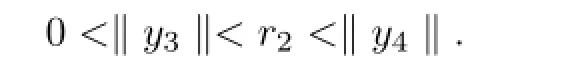
5　实例

例1考虑分数阶差分方程：

取b=10，令

A是一个常数，则

（1）显然（H）成立.

（2）

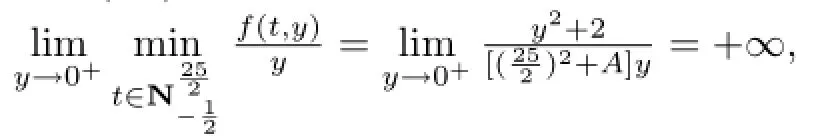
即（H3）成立.

从而由定理4.1可得：分数阶差分边值问题（5.1）至少存在两个正解y1，y2，满足：

例2考虑分数阶差分方程：

取b=10，令

B是一个正的常数，则

（1）显然（H1）成立.

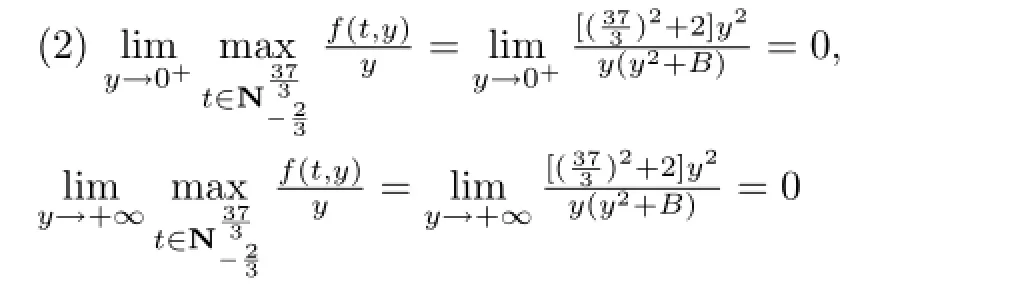
即（H4）成立.

从而由定理4.2可得：分数阶差分边值问题（5.2）至少存在两个正解y3，y4，满足：

［1］Ferreira R A C.Positive solutions for a class of boundary value prob lem s w ith fractional q-differences［J］.Comm put M ath App l，2011，61:367-373.

［2］Benchohra M，Ham ani S，N touyas S K.Boundary value p rob lem s for d ifferential equations w ith fractional order and non local conditions［J］.Nonlinear Anal，2009，71:2391-2396.

［3］Atici F M，Eloe P W.Two-point boundary value p rob lem s for finite fractional difference equations［J］.J Differ Equ App l，2011，17（4）:445-456.

［4］A tici F M，Sengu l S.M odeling w ith fractional difference equations［J］.J M ath Anal App l，2010，369（1）:1-9.

［5］Atici F M，Eloe P W.Two-point boundary value p rob lem s for finite fractional difference equations［J］.J Differ Equ App l，2011，17（4）:445-456.

［6］A tici F M，Uyanik M.Analysis of discrete fractional operators［J］.A pp l Anal Discrete M ath，2015，9（1）:139-149.

［7］程金发.分数阶差分方程理论［M］.厦门:厦门大学出版社，2011.

［8］Good rich C S.On discrete sequential fractional boundary value p rob lem s［J］.J Math Anal Appl，2012，385（1）:111-124.

［9］Good rich C S.Systems of discrete fractional boundary value prob lem s w ith non linearities satisfying no grow th conditions［J］.JDiffer Equ App l，2015，21（5）:437-453.

［10］Lv Weidong.Existenceand uniqueness of solutions for a discrete fractionalm ixed type sumdifference equation boundary value p rob lem［J］.Discrete Dyn Nature Soc，2015，A rticle ID 376261，10 pages.

［11］Luo Xiannan，Guo Shancui.Existence and uniqueness of solutions for fractional boundary value p rob lem w ith fractional boundary value conditions［J］.Qual Theory Dyn Syst，2014，（13）:1-17.

［12］Chen Y i，Tang Xianhua.The difference between a class of discrete fractional and integer order boundary value p roblem s［J］.Comm Nonlinear SciNum er Simu l，2014，（19）:4057-4067.

［13］Lv Zhanm ei，Gong Yanping，Chen Y i，et al.M u ltip licity and uniqueness for a class of discrete fractional boundary value p rob lem s［J］.App l Math，2014，59（6）:673-695.

［14］Holm M.Sum and difference com position in discrete fractional calcu lus［J］.CUBO M ath J，2011，13（3）:153-184.

［15］王金华，向红军，赵育林.一类非线性分数阶差分方程边值问题解的存在性及U lam稳定性［J］.中山大学学报，2016，55（2）:1-13.

M R Su b jec t C lassifica tion:26A 33；39A 10；39A 12

Ex istence ofm u ltip le p ositive solu tions for a boundary value p rob lem of fractional d ifference equation

WANG Jin-hua，X IANG Hong-jun
（College of M athematics and Finance，Xiangnan University，Chenzhou 423000，China）

By constructing the corresponding Green’s function and analysing the key properties with inequality technique，a high order fractionaldifference equation w ith boundary value conditions is studied in this paper.The existence ofmu ltip le positive solutions is obtained by using the fixed point index theory.Additionally，two exam ples are illustrated to guarantee themain resu lts.

multip le positive solution；boundary value p rob lem；fractional difference equation；existence

O 175.7

A

1000-4424（2016）02-0167-09

2015-11-21

2016-05-06

向红军，Em ail：hunxh jxh j67@126.com

国家自然科学基金（11471278）；湖南省自然科学基金（2016JJ6139）