优化的灰色非等距GM(1,1)预测模型在沉降监测中的应用
2016-11-16李志伟李克昭赵磊杰
李志伟,李克昭,2,赵磊杰
(1.河南理工大学 测绘与国土信息工程学院,河南 焦作 454000;2.北斗导航应用技术协同创新中心,河南 郑州 450052)
优化的灰色非等距GM(1,1)预测模型在沉降监测中的应用
李志伟1,李克昭1,2,赵磊杰1
(1.河南理工大学 测绘与国土信息工程学院,河南 焦作 454000;2.北斗导航应用技术协同创新中心,河南 郑州 450052)
初始值的选取和背景值的构造是影响灰色非等距GM(1,1)模型预测精度的两个重要因素。通过最小二乘原理选取非等距GM(1,1)模型的最优初值,利用指数函数法构造新的背景值,构建了优化的灰色非等距GM(1,1)预测模型。最后,结合秀山湖二期工程的沉降实测数据,运用新陈代谢的计算模式进行预测验证,并与传统的非等距GM(1,1)预测模型进行比较。结果表明:基于新陈代谢式优化的非等距GM(1,1)预测模型的拟合精度和预测精度优于传统的非等距GM(1,1)预测模型,新的预测模型的适用性更强。
非等距GM(1,1)模型;最小二乘原理;指数函数;新陈代谢;沉降监测
变形监测预报可用于指导建筑施工、控制施工质量和得到建筑物变形的先验信息。随着科学技术的发展,对建筑物的变形进行监测分析和预报是非常必要的。灰色系统理论是一种研究较少资料、实测数据贫乏以及不确定性问题的理论。变形监测数据本身具有一定的灰性,应用灰色系统理论建立预测模型是合适的。
灰色系统理论的预测模型有多种,其中用于变形监测的灰色预测模型主要有灰色GM(1,1)[1-2],优化的灰色GM(1,1)模型[3-7]以及灰色组合模型[8-10]等。但是,这些模型都是基于等时距序列建立的,而在变形监测的实际工作中,受到各方面因素的影响,时间序列往往是非等距的。基于此,很多学者针对非等距时间序列,构建了灰色非等距GM(1,1)预测模型[11-13],并应用到变形监测工作中,取得了一定的成果。但是,传统的灰色非等距 GM(1,1)预测模型本身固有的系统误差给预测工作造成一定的负面影响,致使预测精度不高。本文通过最小二乘原理选取非等距GM(1,1)模型的最优初值,利用等分函数法构造新的背景值,构建了优化的灰色非等距GM(1,1)预测模型。
1 优化的灰色非等距GM(1,1)预测模型
1.1传统的非等距GM(1,1)模型
传统的非等距GM(1,1)模型是灰色系统理论的预测模型之一,它是以灰色生成函数为基础,以微分拟合为核心的一种建模方法。非等距GM(1,1)模型的建模过程为:
假设一组非负原始数据序列,记为X(0),即
X(0)=[X(0)(t1),X(0)(t2),…,X(0)(tn)]
(1)
式中:tn为观测的时刻;X(0)(tn)为在tn时刻的观测值。
对原始数据X(0)序列进行一次累加,生成的累加数据序列记为X(1),即
X(1)=[X(1)(t1)X(1)(t2),…,X(1)(tn)]
(2)
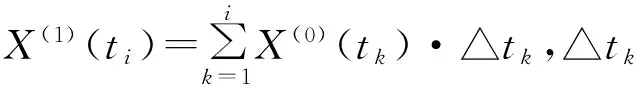
利用最小二乘原理[11-14]计算可得非等距GM(1,1)的预测方程为:

(3)
最后,恢复时间序列还原预测值
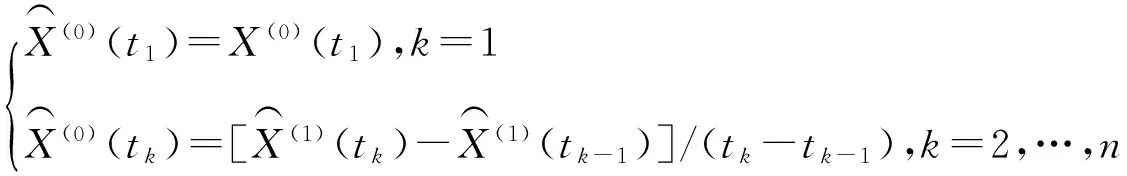
(4)
1.2基于最优初值选取优化的灰色非等距GM(1,1)模型
从式(3)中可以看出,初始值X(1)(t1)作为初始的计算值是不合理的。通过最小二乘原理对初始值进行修正[7],设初始值的修正形式为X(1)(t1)=X(1)(t1)+S,其中S为初始值的修正项。因此,式(3)的预测方程可表示为:

(5)

(6)
将式(6)对S求导,并令其等于0,则S为
S=a1/b1-[X(0)(t1)-a/b]
(7)
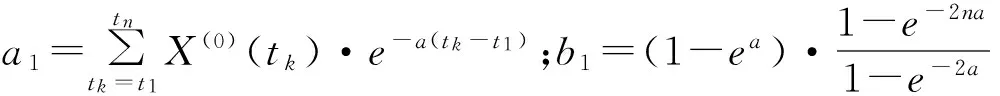
1.3基于指数函数法构造背景值优化的灰色非等距GM(1,1)模型
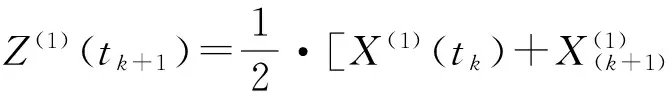

图1 背景值Z(1)序列的构造示意图
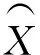
=di·e-a(ti+1-ti)
(8)
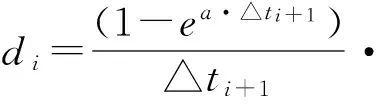
(9)


由X(1)(t1)=X(0)(t1)=D·e-a(t1-t1)+C=D+C可得:
(10)
结合式(8)~式(10)可以得到:
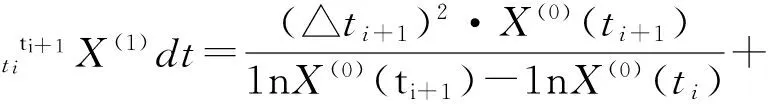
(11)
由式(11)构造新的背景值矩阵B1和向量Y1,得到:
(12)
利用式(12)得出的新背景值和最小二乘原理可求得式(3)的预测方程,最后累减还原时间序列可得到优化的灰色非等距GM(1,1)模型的预测值。
2 优化的灰色非等距GM(1,1)预测模型实例计算与结果分析
对秀山湖二期工程中的7幢楼进行沉降观测(12#、13#、15#、18#、19#、20#、21#)。本文以12#楼为例,由工作基点G3开始对12#楼的沉降点进行观测,按楼层数进行观测,每加盖2层观测1次,前后共观测20次。选取12-2点、12-4点和12-6点中的11期累计沉降数据为原始数据,如表1所示。
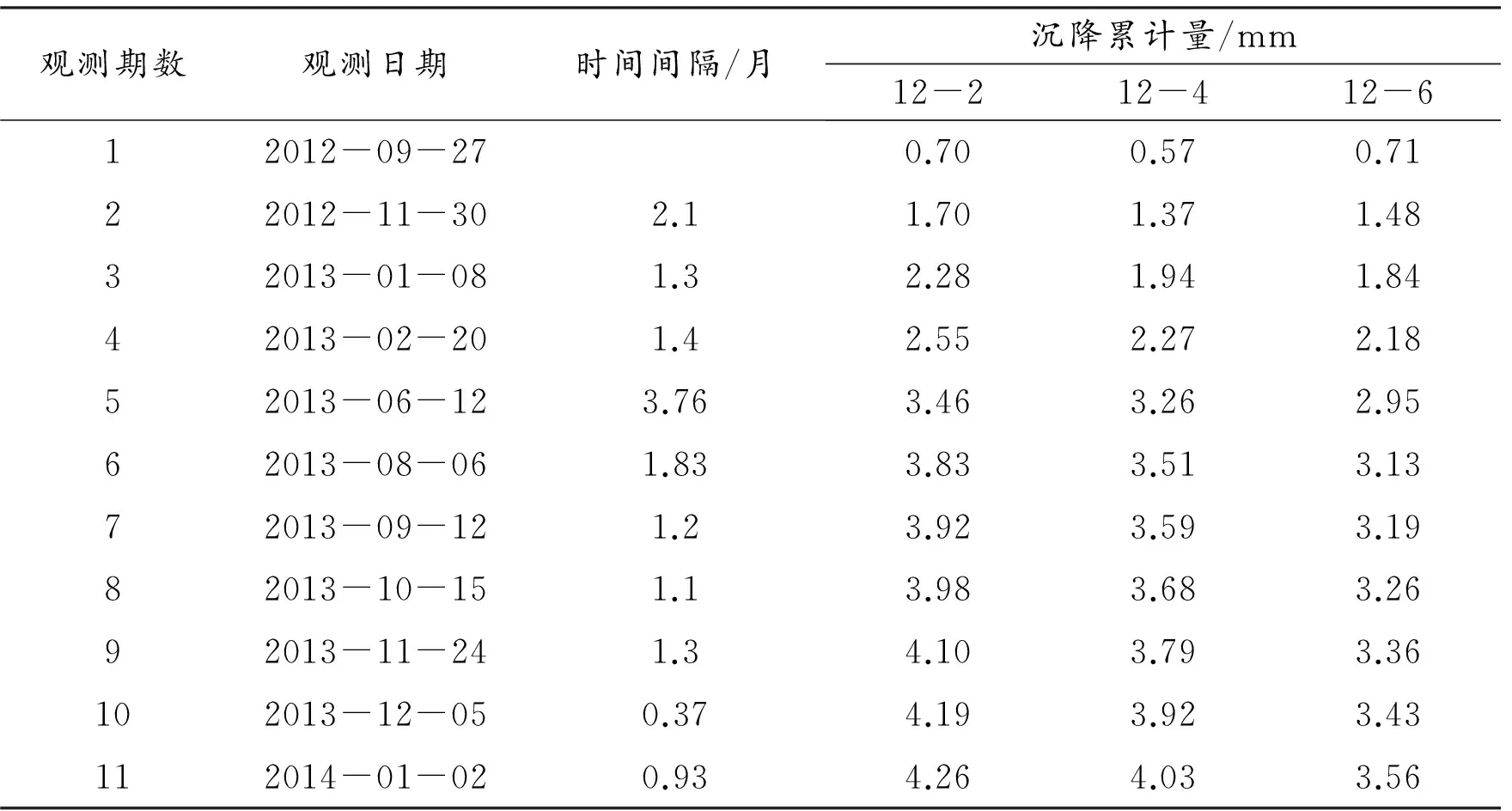
表1 实测沉降累计数据
2.1两种预测模型的拟合结果与分析
利用Matlab 7.0软件为平台,采用新陈代谢的计算方式编写程序,通过表1中前7期沉降累计量数据,预测第8~11期沉降累计量,即:首先利用前7期观测数据建立优化的灰色非等距GM(1,1)预测模型,计算得到第8期累计沉降量的预测值;然后去掉建模数据中的第1期数据,加入第8期的预测值重新建模,再计算第9期累计沉降量的预测值;依次类推,分别计算出第8~11期累计沉降量的预测值;最后,求取新陈代谢过程中产生的拟合值和预测值的平均值,将其作为最终优化的灰色非等距GM(1,1)预测模型的拟合值和预测值。2种预测模型的拟合结果分别如表2、表3所示。

表2 传统的灰色非等距GM(1,1)预测模型的拟合值 mm
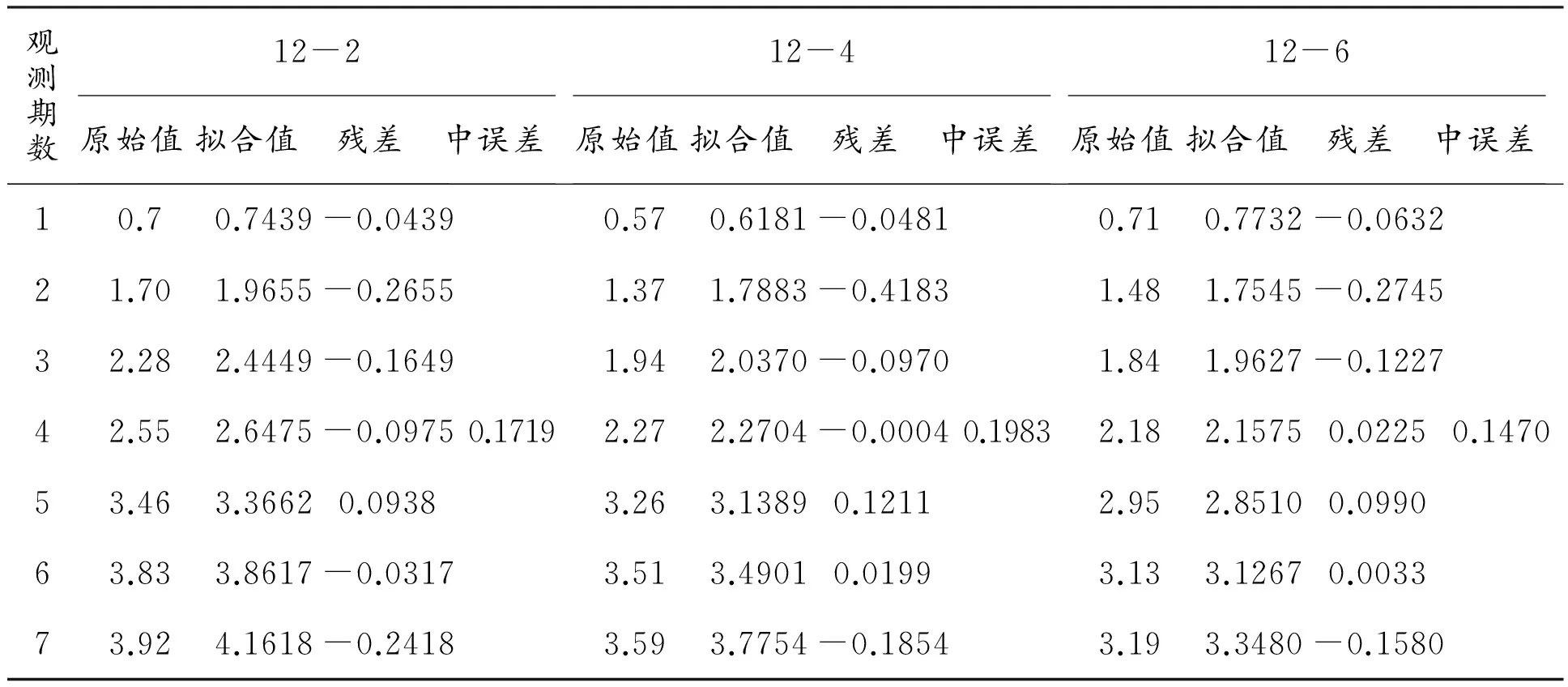
表3 优化的灰色非等距GM(1,1)预测模型的拟合值 mm
从表2和表3中的拟合结果可以看出:12-2点的传统灰色非等距GM(1,1)预测模型的中误差0.287 9 mm大于优化的灰色非等距GM(1,1)预测模型的中误差0.171 9 mm;12-4点的传统灰色非等距GM(1,1)预测模型的中误差0.290 5 mm大于优化的灰色非等距GM(1,1)预测模型的中误差0.198 3 mm;12-6点的传统灰色非等距GM(1,1)预测模型的中误差0.222 5 mm大于优化的灰色非等距GM(1,1)预测模型的中误差0.147 0 mm。基于此,利用3种不同的建模数据验证了优化的灰色非等距GM(1,1)预测模型的拟合精度优于传统的灰色非等距GM(1,1)预测模型。
2.2两种预测模型的预测结果与分析
两种预测模型的预测结果如表4所示。
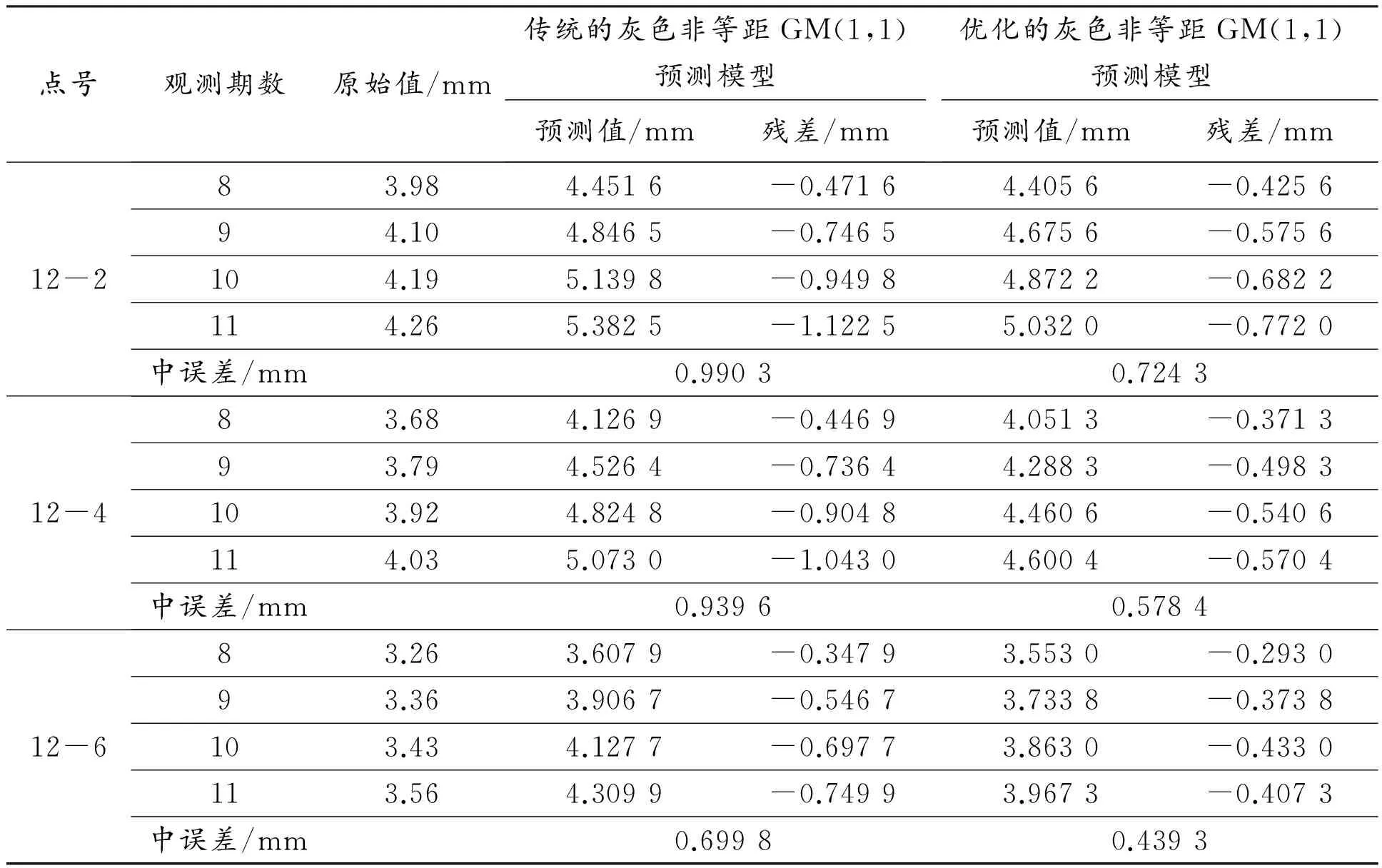
表4 两种预测模型的预测结果 mm
从表4中的模型预测结果得出:12-2点的传统灰色非等距GM(1,1)预测模型的中误差0.990 3 mm大于优化的灰色非等距GM(1,1)预测模型的中误差0.724 3 mm;12-4点的传统灰色非等距GM(1,1)预测模型的中误差0.939 6 mm大于优化的灰色非等距GM(1,1)预测模型的中误差0.578 4 mm;12-6的传统灰色非等距GM(1,1)预测模型的中误差0.699 8 mm大于优化的灰色非等距GM(1,1)预测模型的中误差0.439 3 mm。从计算的结果可以看出:3种不同的建模数据验证了优化的灰色非等距GM(1,1)预测模型比传统的灰色非等距GM(1,1)原模型预测精度更高、实用性更强。
3 结论
针对传统的灰色非等距GM(1,1)预测模型的固有系统误差,本文通过最小二乘原理选取非等距GM(1,1)预测模型的最优初值,利用等分函数法构造新的背景值,构建了优化的灰色非等距GM(1,1)预测模型。最后,结合秀山湖二期工程的变形实测数据,运用新陈代谢的计算模式进行预测验证,并与传统的二色非等距GM(1,1)预测模型进行比较。结果表明:基于新陈代谢式优化的灰色非等距GM(1,1)预测模型的拟合精度和预测精度优于传统的灰色非等距GM(1,1)预测模型,新的预测模型的适用性更强,具有一定的参考价值。在建模过程中,要充分考虑建模数据的相关程度,建议建模数据不要低于6期为宜,外推的预测值不要超过4期为宜,同时应根据实测数据,及时地更新建模数据,用最新的、更可靠的数据建立预测模型。
[1]岳仁宾,腾德贵,胡波,等.灰色模型在深基坑变形监测中的应用研究[J].测绘通报,2014(s1):85-87.
[2]陈俊杰,郭延涛.基于灰色系统理论的概率积分法参数确定研究[J].测绘通报,2012(s1):116-118.
[3]郭兰兰,邹志红,安岩.基于残差修正的GM(1,1)模型在水质预测中的应用[J].数学的实践与认识,2014,44(19):176-181.
[4]谭冠军.GM(1,1)模型的背景值构造方法和应用[J].系统工程理论与实践,2000,20(4):99-103.
[5]袁德宝, 崔希民, 高宁. 同时利用x(1)(1)和x(1)(n)为GM(1,1)建模初始条件的预测方法研究[J].大地测量与地球动力学, 2013, 33(3):79-82.
[6]李世贵,易庆林,吴娟娟,等.背景值优化的多点灰色模型在滑坡变形预测中的应用[J].中国地质灾害与防治学报,2015,26(2):3-9.
[7]张彬, 西桂权. 基于背景值和边值修正的GM(1,1)模型优化[J].系统工程理论与实践,2013,33(3):682-688.
[8]沈哲辉,黄腾,唐佑辉.灰色-马尔科夫模型在大坝内部变形预测中的应用[J].测绘工程,2015,24(2):69-74.
[9]吴浩,董元锋,李奎,等.灰色系统和几何耦合的边坡变形预测模型研究与应用[J].测绘通报,2014(s1):46-49.
[10]高宁,崔希民,高彩云.高层建筑物沉降变形的灰线性预测[J].测绘科学,2012,37(3):96-98.
[11]王鸣翠,于胜文,张帅帅,等.基坑变形非等时距灰色预测模型程序设计及应用[J].测绘地理信息,2015,40(1):41-44.
[12]成枢,李强.基于非等间隔GM(1,1)模型的沉降预测[J].测绘与空间地理信息,2015,38(4):33-35.
[13]李军亮,肖新平,廖锐全.非等间隔GM(1,1)幂模型及应用[J].系统工程理论与实践,2010,30(3):490-495.
[14]王叶梅,党耀国,王正新.非等间距GM(1,1)模型背景值的优化[J].中国管理科学,2008,16(4):159-162.
Application of optimized non-equidistance GM(1,1) prediction model in subsidence monitoring
LI Zhi-wei1,LI Ke-zhao1,2,ZHAO Lei-jie1
(1.SchoolofSurveyingandLandingInformationEngineering,HenanPolytechnicUniversity,Jiaozuo454000,China;2.CollaborativeInnovationCenterofBDSResearchApplication,Zhengzhou450052,China)
The original values,conformation of background values perform important double factors to the precision of the gray Non-equidistance GM (1,1) model.In this paper,we selected the optimal initial values of the Non-equidistance GM(1,1) model by the least square principle,created new background values by exponential function method,producing the optimized gray Non-equidistance GM(1,1) prediction model.Combined with data of the subsidence monitoring of the second phase of Xiu Shan Lake project,the metabolism computing model is used to prediction and we effectively compared the traditional Non-equidistance GM(1,1) model and the optimized Non-equidistance GM(1,1) model.The results show that the optimized Non-equidistance GM (1,1) prediction model based on the Metabolism prediction model of the accuracy is better than the traditional Non-equidistance GM(1.1) prediction model,new prediction model performed better applicability,which has practical reference value.
non-equidistance GM (1,1);the least square principle;exponential function;metabolism;subsidence monitoring
2015-12-02
国家自然科学基金资助项目(41202245;41272373)
李志伟(1991—),男,河南卫辉人,硕士研究生。
1674-7046(2016)02-0068-06
10.14140/j.cnki.hncjxb.2016.02.013
TU196+.1
A
