基于单基频S变换的电压凹陷分类

程　焰，易吉良，张　帅，杨晓芳，刘小文

（湖南工业大学 电气与信息工程学院，湖南 株洲 412007）

基于单基频S变换的电压凹陷分类

程焰，易吉良，张帅，杨晓芳，刘小文

（湖南工业大学 电气与信息工程学院，湖南 株洲 412007）

针对S变换计算量大的问题，提出了一种基于单基频S变换的电压凹陷分类方法。首先通过单基频S变换得到单基频S变换模向量；然后，从该向量提取凹陷信号幅值突变点个数、凹陷幅值和凹陷幅值标准差等特征量；最后，将这些特征量输入决策树对电压凹陷信号进行分类。仿真结果验证了该方法对电压凹陷分类的有效性。

单基频S变换；电压凹陷；幅值突变点；凹陷幅值；凹陷幅值标准差

0　引言

当代电力负荷中，复杂电子设备得到了广泛应用。但这些敏感电子设备对短时间的电压变化较为敏感，电压凹陷是使其不能正常工作的主要原因。分析电压凹陷产生的原因和发生的类别，对于有针对性地采取治理措施具有重要意义。

国内外学者对电压凹陷分类问题进行了大量深入的研究［1］。常用以小波为代表的时频分析方法作为分类工具［2-3］，而近期S变换因具有更直观的时频特性和无需选择小波函数等优点成为研究热点。文献［4］提出了基于S变换的标准模板相似度的电压凹陷分类方法，依据模板相似度最大原则，实现了任意持续时间长度的凹陷信号分类，该方法在噪声情况下能对暂降信号进行准确分类。文献［5］根据S变换模时频矩阵检测扰动信号的时频域特征，再利用时频域特征对电能质量进行检测和识别，该方法抗干扰性好。文献［6］采用改进不完全S变换与决策树相结合的方法对电能质量扰动进行分类，通过动态测度对改进不完全S 变换结果进行特征提取，再利用优化决策树对电能质量扰动进行分类。文献［7］采用改进S变换对不同原因引起的电压凹陷进行分类，提取凹陷幅值、凹陷时刻和相位等特征量，利用分类判决规则对凹陷扰动源进行正确识别，该方法能正确识别3种暂降扰动源。文献［8］提出了基于改进S变换的电压暂降识别方法，通过分频逐行计算相似度值，分析各类凹陷的差异，实现扰动分类。上述基于S变换或改进S变换的电压凹陷分类方法中，在S变换运算过程中，对所有频率点进行了计算，因此，算法的运算量大，运算时间长，实时性较差［9-10］。

在S变换计算过程中，若只利用基频向量，则可大大减少运算时间。基于上述思想，本文提出了基于单基频S变换（single fundamental frequency S-transform，SFST）的电压凹陷分类方法。本文先对基频频率点加高斯窗进行IFFT（inverse fast Fourier transform）运算，得到电压凹陷分析所需的基频向量，以最大限度地减少S变换的运算量；再求取SFST的模向量，提取相关特征量，利用决策树对4种电压凹陷进行分类识别［11］。最后，利用MATLAB进行仿真试验，验证了本文方法的有效性。

1　S变换

S变换是对连续小波变换和短时傅里叶变换的发展［12］。信号h（t）的一维连续S变换S（， f）定义为

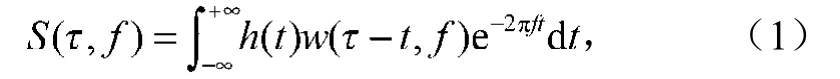
式中：为调节高斯窗口的参数；

f为频率；

t为时间；

w（-t， f）为高斯窗口，即

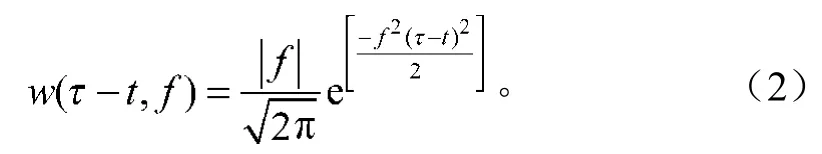
由式（2）可以看出，高斯窗口的高度和宽度随频率改变。S变换克服了短时傅里叶变换中窗口高度和宽度固定的缺陷［13-14］。

S变换的离散形式为：

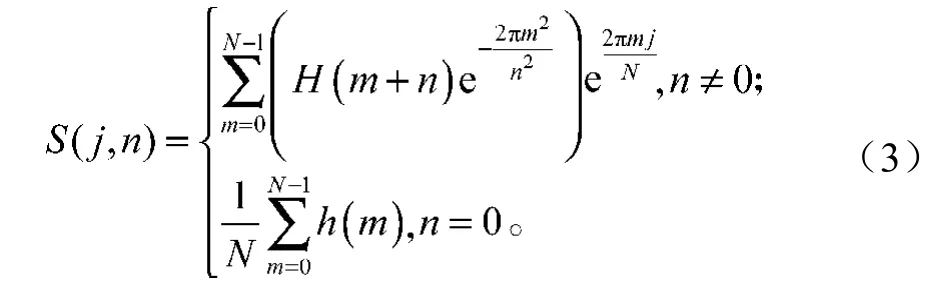
式中：j， n分别为时间采样点和频率采样点，j， n =0，1， …，N-1；

N为总采样点数；

H（m+n）为信号h（t）的离散傅里叶变换的移位运算；

h（m）为对连续时间信号h（t）进行采样得到的离散时间序列。

由式（3）可以看出，S变换可由快速傅里叶变换（fast fourier transform，FFT）实现快速计算，其计算结果为一个复时频矩阵。因此，可从S变换模时频矩阵的基频向量中提取相关特征量，来对电压凹陷进行分类。该方法除计算基频向量外，还计算了其他无用向量，导致运算时间较长。

2　SFST算法介绍

2.1SFST原理

将S变换应用于电压凹陷分类时，本文只对基频频率点进行计算，故定义SFST为

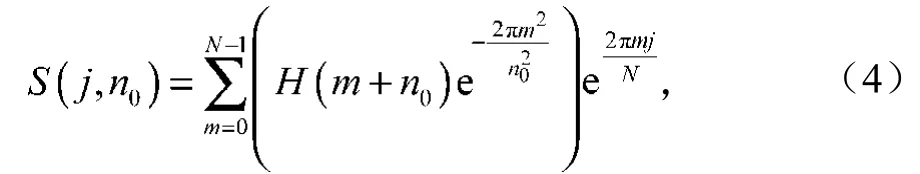
式中n0为基频频率采样点，与信号总时长有关系。n0和实际频率f0的换算关系为

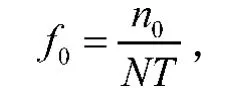
式中T为采样周期。通过式（4）得到一维复数向量，对其求模，得到基频模向量。

SFST的计算过程与S变换基本类似，区别在于S变换对所有频率点都进行运算，而SFST只针对基频频率点进行计算。SFST的计算过程如图1所示。

图1　SFST基本原理框图Fig.1　Diagram of the fundamental principles of SFST

由图1可以看出，SFST的基本流程是：先将输入的电压凹陷信号进行FFT变换，得到离散傅里叶变换h（m），再进行移位运算，得到H（m+n0）；计算高斯窗G（n0， m），其中n0为窗中心；再进行加窗运算H（m+n0）×G（n0， m），对加窗运算后的结果做IFFT变换，得到单基频S变换复数向量S（j， n0）；最后输出电压凹陷的SFST模向量信号。

2.2特征量提取

本文考虑4种类型的电压凹陷。为了方便表述，将故障引起的记为A类凹陷；异步电动机引起的记为B类凹陷；变压器励磁涌流引起的记为C类凹陷；故障自清除引起的记为D类凹陷。凹陷持续时间和幅值取文献［3］中的参数取值范围，4种类型的电压凹陷模型表达式如表1所示。表1中的变量名含义如下：w为角频率；b， b1为幅值，0.1＜b＜0.9，0.1＜b1＜0.3；t为电压凹陷的持续时间，不同凹陷信号的持续时间段有差别。

表1　电压凹陷的信号模型表达式Table 1　Signal model expression of voltage sags

根据表1电压凹陷的信号模型，得到电压凹陷信号如图2所示。

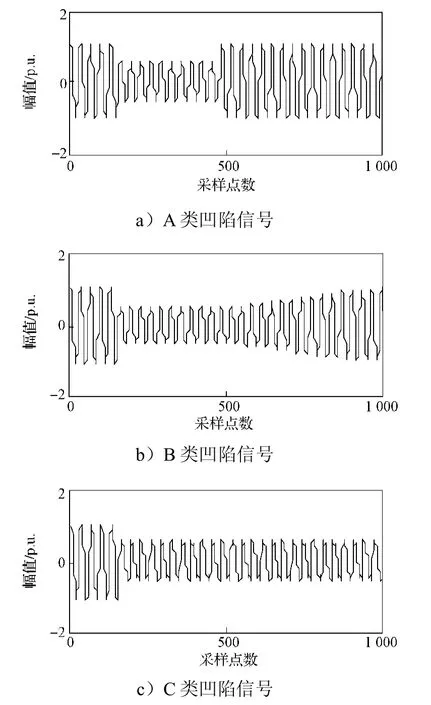
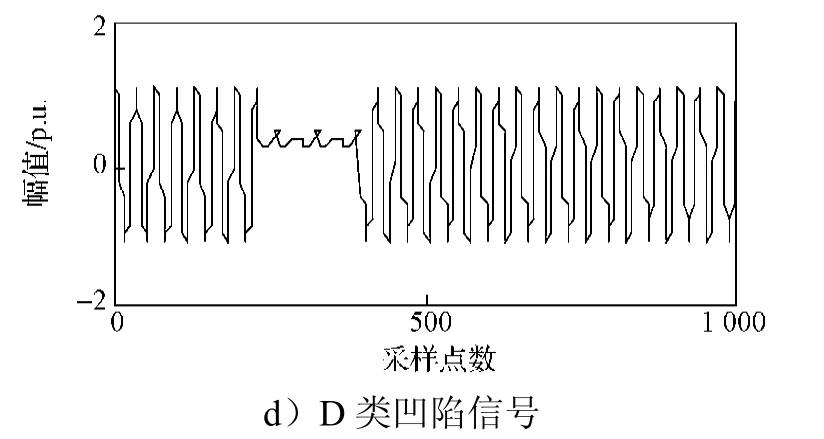
图2　电压凹陷信号Fig.2　Voltage sag signals

由图2可以看出：A类凹陷信号在开始和结束时刻伴有幅值的突变，形状类似长方形；B类凹陷信号恢复正常状态的过程相对缓慢，且该类凹陷只具有一次明显幅值的突变；C类凹陷信号可持续相对较长时间；D类凹陷信号持续时间最短，凹陷期间幅值很小，会导致较大的幅值突变。

为了更加明确地区分这4类电压凹陷信号，本文利用SFST得到4类电压凹陷信号相应的基频模向量，如图3所示。

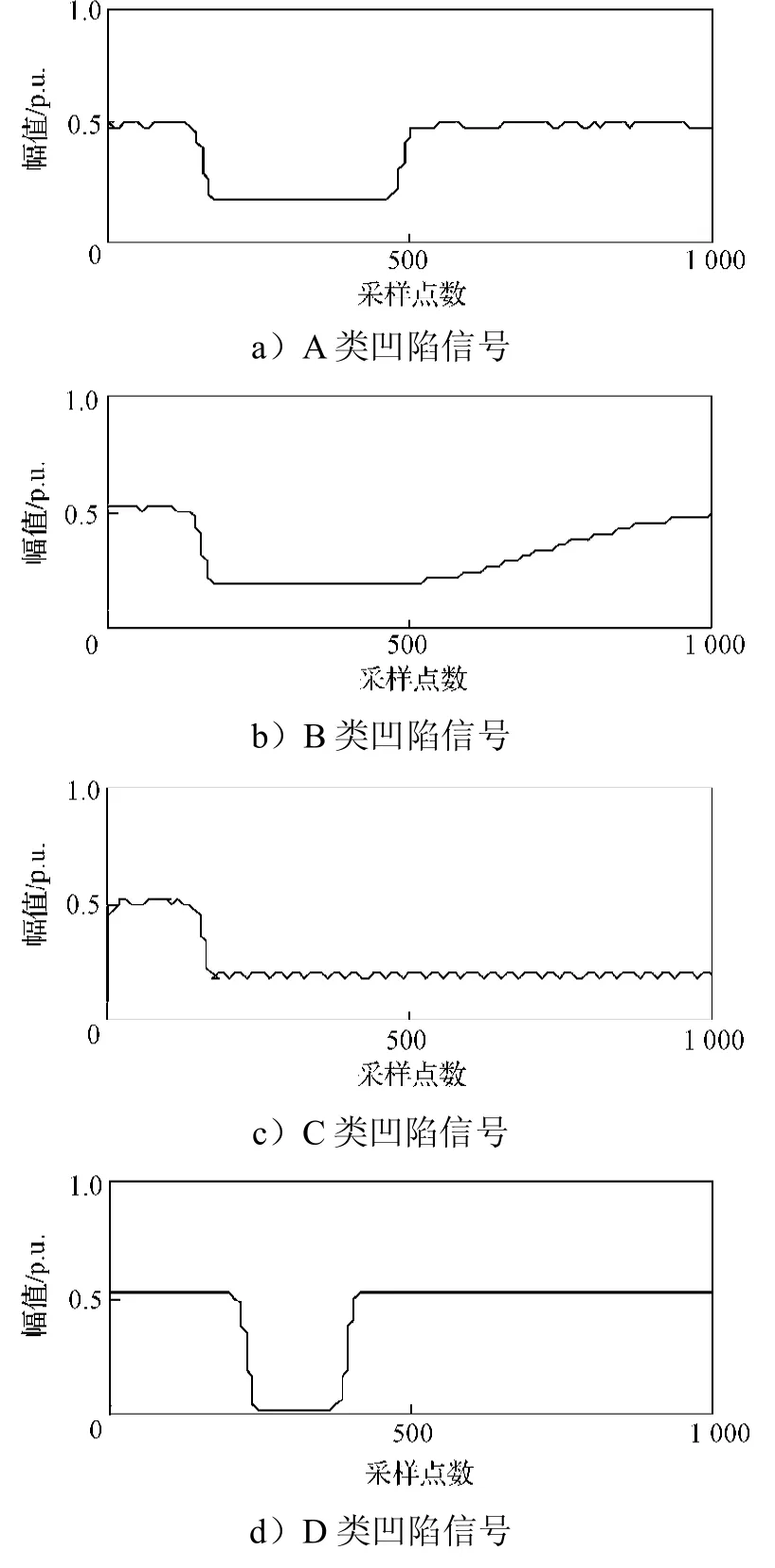
图3　电压凹陷信号的SFST模向量Fig.3　SFST mode vector of voltage sag signals

由图3可以看出，从SFST模向量提取3种特征量，即凹陷信号幅值突变点个数（F1）、凹陷幅值（F2）和凹陷幅值标准差（F3），能有效对上述4种凹陷信号实现分类［14-15］。

1）F1反映凹陷发生时刻和凹陷结束时刻是否存在幅值突变，如果凹陷起止时刻都有突变，则F1的值为2，否则为1。由图3可以看出，B类和C类凹陷的特征量F1值为1；A类和D类凹陷的特征量F1值都为2。

2）F2反映电压降落程度，可通过检测SFST模向量差分的极值进行定量求取。当幅值突变时，突变的向量差分绝对值比起非突变的会大很多。不同原因引起的凹陷幅值会有差异。由图3可以看出，A类凹陷幅值明显大于D类。经测试发现，当F2小于0.05时，为D类凹陷信号；否则，为A类凹陷信号。

3）F3反映各类凹陷信号在凹陷持续过程中凹陷幅值的变化情况。本文采用MATLAB产生不同凹陷时间的B， C类凹陷信号，再对B， C类凹陷在跌落点后SFST模向量幅值标准差进行对比研究，分析F3的变化情况。B， C类凹陷信号F3在不同凹陷时间的分布情况如图4所示。图中，T1， T2， T3分别对应凹陷突变点后第2个周期、第8个周期和第15个周期。

由图4可以看出，B， C两类凹陷的特征量F3差异明显，B类凹陷特征量F3值明显高于C类；B类凹陷特征量F3随着凹陷幅值的增大而减小，而 C类凹陷特征量F3几乎没有变化。因此，B类和C类凹陷可以很好区分。经测试发现，当F3大于0.01时，为B类凹陷，否则，为C类凹陷。

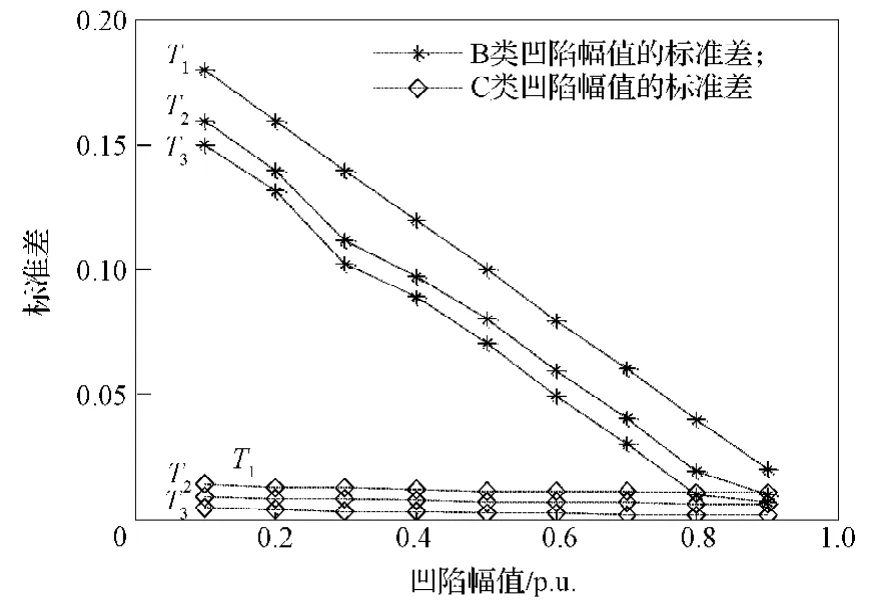
图4　B， C类电压凹陷幅值对应的标准差Fig.4　Corresponding standard deviation for B and C-type voltage sag amplitudes

2.3分类原理

基于SFST原理，以及对4类电压凹陷特征量的计算与分析，本文采用决策树对电压凹陷进行分类［16-20］，分类原理如图5所示。首先，根据特征量F1可以确定输入信号是属于A， D类或B， C类；若是A， D类，则根据F2确定为A类或D类；若是B， C类，则根据F3确定为B类或C类。这样能实现4类凹陷信号的分类。

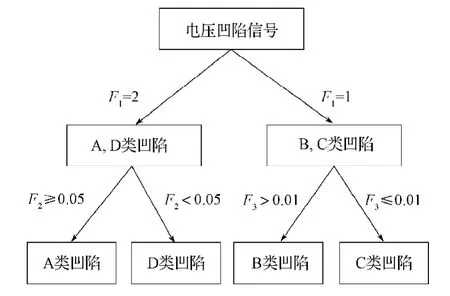
图5　电压凹陷分类原理图Fig.5　Schematic diagram for the classification of voltage sags

算法流程如图6所示。首先，将电压凹陷信号进行SFST变换；其次，求S模向量；然后，通过向量得到特征量F1～F3；最后，将特征量输入决策树，根据特征量阈值对电压凹陷进行分类。

图6　算法流程图Fig.6　Algorithm flow chart

3　仿真分析

利用MATLAB随机产生A， B， C， D四类电压凹陷波形信号各200个测试样本，采样频率为1.6 kHz，基频频率为50 Hz。对每个测试样本分别叠加20， 40 dB的噪声后，进行仿真试验，分类结果如表2和表3所示。从表2和表3可以看出，各类凹陷识别正确率达到99%以上，说明本文电压凹陷分类方法准确率较高，而且对噪声不敏感。

为验证SFST电压凹陷分类方法相比于S变换分类方法在运算效率方面的优势，测试了不同数据点数情况下SFST和S变换的运算时间，结果如表4所示。由表4可以看出，随着数据量的增加，S变换的运算时间呈指数增长，数据量为6 400时，计算时间达到6 788.1 ms，因此，S变换的实时性很差；随着数据量的增加，SFST的运算时间也会增加，当数据量为6 400时，其计算时间约为S变换的千分之一，因此，本算法的实时性较好。

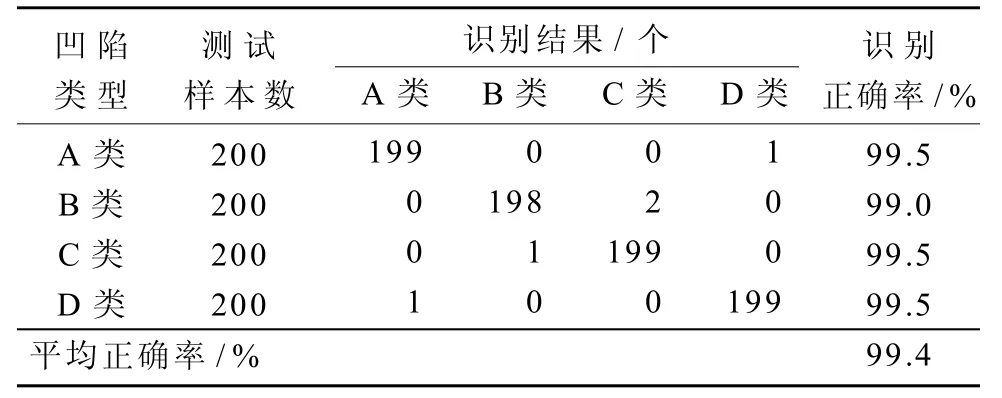
表2　20 dB噪声下4类凹陷信号的识别结果Table 2　Diagnostic results of 4 kinds of sag signals under 20 dB noise

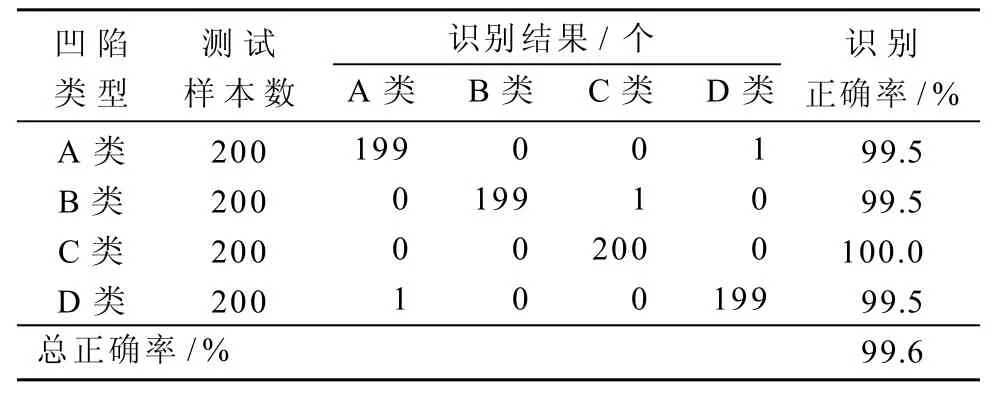
表3　40 dB噪声下4类凹陷信号的识别结果Table 3　Diagnostic results of 4 kinds of sag signals under 40 dB noise

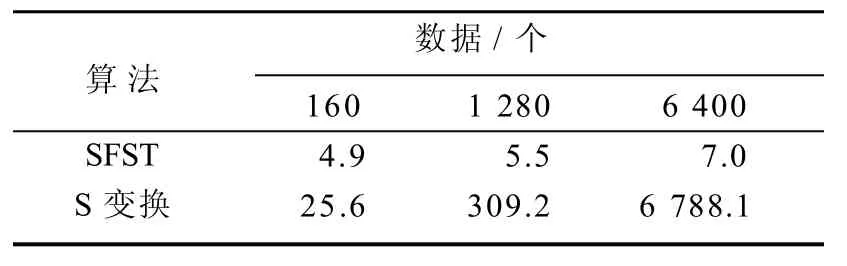
表4　SFST和S变换的运算时间对比Table 4　Comparison of computation time between SFST and S-transform　ms

4　结论

本文提出了基于SFST模向量特征量和决策树的电压凹陷分类方法。测试了本文方法对4种常见电压凹陷信号的分类效果，比较了本文方法和S变换的运算时间。具体结论如下。

1）电压凹陷信号经SFST后，基频幅值模向量能凸显4类凹陷信号的特征，且噪声干扰影响小。各类凹陷的识别正确率达到99%以上。

2）相对于S变换，SFST只需计算基频模向量，大大降低了计算量，减少了运算时间。

因此，本文选取的特征量及分类方法是可行的、有效的。

［1］肖湘宁.电能质量分析与控制［M］.北京：中国电力出版社，2010，28-32.XIAO Xiangning.Power Quality Analysis and Control［M］.Beijing：China Electric Power Press，2010，28-32.

［2］鲁波涌，黄文清.结合小波变换和能量算子的电压暂降检测方法［J］.电工技术学报，2011，26（5）：171-177.LU Boyong，HUANG Wenqing.Hybrid Wavelet Energy Operator Methods for Voltage Sag Detection［J］.Transactions of China Electrotechnical Society，2011，26（5）：171-177.

［3］王克星，宋政湘，陈德桂，等.基于小波变换的配电网电压暂降的干扰源辨识［J］.中国电机工程学报，2003，23（6）：29-34.WANG Kexing， SONG Zhengxiang， CHEN Degui， et al.Interference Source Identification of Voltage Sag in Distribution System Based on Wavelet Transform［J］.Proceedings of the CSEE，2003，23（6）：29-34

［4］李康瑞，杨洪耕.基于S变换标准模板相似度的电压暂降分类［J］.电工技术学报，2010，25（12）：139-146.LI Kangrui，YANG Honggeng.S-Transform Based on Classification for Voltage Dips According to Standard Template Similarity［J］.Transactions of China Electronical Society，2010，25（12）：139-146.

［5］孙楚平，杨旭.基于S变换模时频矩阵的电能质量扰动检测与识别［J］.电力系统保护与控制，2013，40（7）：60-65.SUN Chuping，YANG Xu.Detection and Recognition of Power Quality Disturbance Based on Module Time-Frequency Matrixes by S-Transform［J］.Power System Protection and Control，2013，40（7）：60-65.

［6］郭俊文，李开成，何顺帆，等.基于改进不完全S变换与决策树的实时电能质量扰动分类［J］.电力系统保护与控制，2013，41（22）：103-110.GUO Junwen，LI Kaicheng，HE Shunfan，et al.A Real Time Power Quality Disturbance Classification Based on Improved Incomplete S-Transform and Decision Tree［J］.Power System Protection and Control，2013，41（22）：103-110.

［7］全惠敏，戴瑜兴.电压暂降的改进S变换分析与分类［J］.湖南大学学报（自然科学版），2011，38（3）：45-50.QUAN Huimin，DAI Yuxing.Detection and Classification of Voltage Sags Based on Modified S-Transform［J］.Journal of Hunan University（Natural Sciences），2011，38（3）：45-50.

［8］徐方维，刘亚梅，杨洪耕，等.基于改进 S变换的电压暂降识别［J］.电力系统保护与控制，2013，41（17）：18-24.XU Fangwei，LIU Yamei，YANG Honggeng，et al.Voltage Sags Identification Based on Generalized S-Transform［J］.Power System Protection and Control，2013，41（17）：18-24.

［9］易吉良，彭建春.基于广义S变换的短时电能质量扰动信号分类［J］.电网技术，2009，33（5）：22-27.YI Jiliang，PENG Jianchun.Classification of Short-Time Power Quality Disturbance Signals Based on Generalized S-Transform［J］.Power System Technology，2009，33（5）：22-27.

［10］占勇，程浩忠，丁屹峰，等.基于 S 变换的电能质量扰动支持向量机分类识别［J］.中国电机工程学报，2005，25（4）：51-56.ZHAN Yong，CHENG Haozhong，DING Yifeng，et al.S-Transform-Based Classification of Power Quality Disturbance Signals by Support Vector Machines［J］.Proceedings of the CSEE，2005，25（4）：51-56.

［11］HE Shunfan，LI Kaicheng，ZHANG Ming.A New Transient Power Quality Disturbances Detection Using Strong Trace Filter［J］.IEEE Transactions on Instrumentation and Measurement，2014，64（12）：2863-2871.

［12］ TAYJASANANT T，SURISUNTHON S.Impacts of Distributed Generation on Voltage Sag Assessment in Thailand’s Distribution Systems［C］//2012 IEEE 15th International Conference on Harmonics and Quality of Power.Hong Kong：IEEE，2012：624-629.

［13］STOCKWELL R G，MANSINHA L，LOWE R P.Localization of the Complex Spectrum：The S Transform［J］.IEEE Transactions on Signal Processing，1996，44（4）：998-1001.

［14］DE MAESSCHALCK R，JOUAN-RIMBAUD D，MASSART D L.The Mahalanobis Distance［J］.Chemometrics and Intelligent Laboratory Systems，2000，50（1）：1-18.

［15］MLADEN K，YUAN L.A New Method for Classification and Characterization of Voltage Sags［J］.Electric Power Systems Research，2001，58（1）：27-35.

［16］肖娟，唐邵玲.决策树和判别分析在分类问题中的比较研究［J］.湖南工业大学报，2008，22（3）：27-31.XIAO Juan，TANG Shaoling.Comparison Research on Decision Tree and Distinction Analysis in Classified Questions［J］.Journal of Hunan University of Technology，2008，22（3）：27-31.

［17］石贵民.武夷山九曲溪湿地鸟类联网监测及识别系统［J］.湖南工业大学报，2013，27（2）：84-88.SHI Guimin.The Birds-Networking Monitoring and Recognition System in Nine Turns Stream Wetland of Mt.Wuyi［J］.Journal of Hunan University of Technology，2013，27（2）：84-88.

［18］徐鹏，林森.基于C4.5 决策树的流量分类方法［J］.软件学报，2009，20（10）：2692-2704.XU Peng，LIN Sen.Internet Traffic Classification Using C4.5 Decision Tree［J］.Journal of Software，2009，20（10）：2692-2704.

［19］关晓蔷.基于决策树的分类算法研究［D］.太原：山西大学，2006.GUAN Xiaoqiang.Research on the Classifying Algorithm Based on Decision Tree［D］.Taiyuan：Shanxi University，2006.

［20］陈沛玲.决策树分类算法优化研究［D］.长沙：中南大学，2007.CHEN Peiling.Research on the Algorithm Optimization of Decision Trees Classification［D］.Changsha：Central South University，2007.

（责任编辑：邓彬）

Classification of Voltage Sags Based on Single Fundamental Frequency S-Transform

CHENG Yan，YI Jiliang，ZHANG Shuai，YANG Xiaofang，LIU Xiaowen
（School of Electrical and Information Engineering，Hunan University of Technology，Zhuzhou Hunan 412007，China）

In view of the large computational quantity involved in the S-transform， a new classification of voltage sags， which is based on single fundamental frequency S-transform， has been proposed for its improvement.First， the acquisition of module vector is achieved through S-transform of single fundamental frequency， followed by the extraction of such characteristic parameters as mutation point numbers， sag magnitude and sag amplitude standard deviation from this vector.Finally， a classification is made of voltage sag signals based on the characteristic parameters input in the decision tree.Simulation results show that the proposed method is effective for the classification of voltage sags.

single fundamental frequency S-transform；voltage sag；amplitude change point；sag amplitude；sag amplitude standard deviation

TM714.2

A

1673-9833（2016）04-0021-06

10.3969/j.issn.1673-9833.2016.04.005

2016-04-14

国家自然科学基金资助项目（61503131），湖南省教育厅科学研究基金资助项目（14C0327）

程焰（1992-）女，湖南常德人，湖南工业大学硕士生，主要研究方向为电力系统自动化，E-mail：719833717@qq.com

易吉良（1972-）男，湖南株洲人，湖南工业大学副教授，主要研究方向为电能质量分析，数字信号处理，E-mail：yi.jiliang@163.com