基于线性二次型最优控制的小水电自并励励磁控制器设计★

邓昭俊，雷敏，曾进辉，李丹

（湖南工业大学 电气与信息工程学院，株洲 412007）

基于线性二次型最优控制的小水电自并励励磁控制器设计★

邓昭俊，雷敏，曾进辉，李丹

（湖南工业大学 电气与信息工程学院，株洲 412007）

随着电能质量与电能需求的要求不断提高，小水电发电机励磁系统的稳定性成为了当今重要的研究课题。本文以提高小水电发电机励磁系统的稳定性为目的，在线性二次型最优控制理论下，建立了单机无穷大系统的状态方程，设计了以机端电压、角速度、有功功率为反馈量的线性二次型7MW最优自并励励磁控制器。在单机无穷大系统下用MATLAB仿真软件对大、小两种扰动进行算例仿真，且对比了AVR+PSS。仿真结果表明本文设计的最优控制器具有较好的阻尼性和动态性，具有一定的实际应用价值。

线性二次型；最优控制；自并励励磁控制器

0 引言

励磁系统是同步发电机的重要组成部分。从某种程度上看，励磁系统决定了同步发电机输出的电能质量。AVR+PSS的控制方式是在低频振荡不足的条件下诞生的。由于它在控制方面具有突出的效果，所以，直到今天仍在广泛地使用，随着电能质量与电力系统的要求逐渐地提高，相比之下，这种控制方式出现了一些障碍。一些新型的控制方式在现代控制理论的发展中脱颖而出，而最优控制理论就是其中的一种，它具有独特的优点[1]，是现代控制理论中比较完善的一种。基于多变量的励磁控制方式要比单变量的励磁控制方式所取得的控制性能要好，多变量励磁调节方式也是未来励磁调节方式的发展方向之一[2]。所以本文基于多变量的线性最优算法励磁控制方式的励磁调节器的仿真研究是设计最优控制器的重要方法与手段。

本文的目的就是在线性二次型最优控制的基础上设计7MW的励磁控制器，通过MATLAB的仿真，对比AVR+PSS控制下的励磁控制系统与最优控制下的励磁系统在小扰动下的静态特性与大扰动下的暂态特性，从而，既可以证明最优控制比AVR+PSS控制更好，又可以验证最优控制的7MW励磁控制器的设计是更好的。

1 水电站自并励发电机励磁系统建模

1.1 自并励励磁系统的组成

图1就是自并励静态励磁系统的结构图。从整体来看，发电机励磁绕组的电源来自发电机，

只不过，这种电能不是由发电机直接输出的，而是由变压器变换电能后通过整流装置变换获得的。励磁控制器的控制量是非常灵活的，既可以是电压互感器的二次电压，又可以是附加的电流互感器的二次电流，还可以是发电机的转速与电磁功率。发电机的运行状况是随着电网的运行变化而变化的，同时，励磁控制器都可以采集到这些变化量，通过这种变化量，调节可控整流装置的控制角，从而就可以改变发电机的励磁[3-5]。

1.2 单机-无穷大系统的数学模型

从宏观上来看，发电机有三个绕组，分别是定子绕组、转子绕组以及阻尼绕组，而这几个绕组之间都存在磁耦合，同时由于转子的位置在不断地变化，这必然导致绕组之间的磁耦合与转子位置存在着函数系。所以，励磁控制系统的模型是非常复杂的，也是一个随着时间而变化的动态过程。在一定的约束范围下，一个简单的模型可以代替一个复杂的模型，因为那些次要的因数对整个励磁控制系统的影响并不大。因此，可以采用图2所示的单机——无穷大母线输电系统的数学模型[6-7]。

图1 自并励励磁系统结构图Fig.1 Independent the shunt excitation system structure

图2 单机—无穷大系统Fig.2 Single - infinity system

2 自并励发电机励磁系统线性二次型最优控制器设计

2.1 线性最优控制原理

线性最优控制原理就是选取最优的控制规律，在特定的指标约束条件下让控制系统性能达到最优。最优控制系统框图3所示。

线性定常系统状态空间方程的一般形式为：

式中，A为状态系数矩阵；B为控制系数矩阵；X为n维状态向量；U为r维控制向量。

图3 最优控制框图Fig.3 The optimal control block diagram

如图3所示，可以引入状态反馈构成闭环系统以达到改善系统性能。反馈系统的状态向量为：

式中，K为状态反馈增益矩阵。

将式（1）和式（2）合并，可以得到：

由（3）可见，最优控制的本质就是选取反馈矩阵K，以使它在给定控制规律下达到特定条件下的最优[8-11]。

2.2 二次型性能指标

假定y（t）为系统的实际响应，ξ(t)为系统预期的响应。最优控制性能指标是使两者的偏差最小，即

式中，J是随函数y(t)而变化的一个泛函数，是在0～∞时间内求取偏差平方的积分，称为二次型指标。如果以X(t)为实际状态向量，以X(t)为预期状态向量，则要求状态向量偏差最小的二次型性能指标为：

在二次型性能指标中，也需要引入控制量约束。如果没有这个约束，所设计的控制器中，控制量的变化范围可能会很大，难以实现。引入控制量约束的二次型指标为：

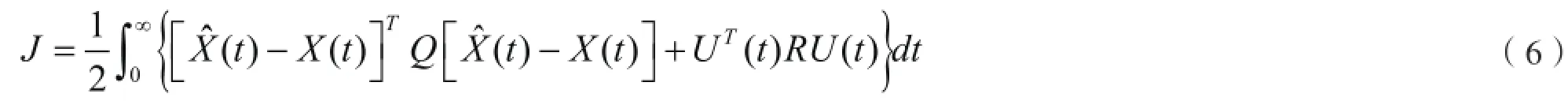
式中Q和R分别表示态向量和控制向量的权矩阵。

为了便于分析，通常把系统平衡点置于状态空间的原点，即X（t）=0，则式（6）可以变换为：

公式（7）作为性能指标设计最优控制系统的唯一依据，而且可以证明这个最优控制规律是存在且唯一的，表达式为：

式中，K为最优反馈增益矩阵。P为n x n维对称常矩阵，矩阵P是黎卡梯方程：

2.3 线性二次型最优控制器的数学模型

本文的研究对象是建立在某水电站7MW的水轮发电机上，利用可控硅的自并励励磁方式，建立比较精准的同步发电机数学模型七阶派克模型[13]。由于转子绕组的时间常数与定子绕组的时间常数大得多，所以，在建立线性最优励磁控制器的数学模型时，可以忽略不计，而且在满足一定的约束范围内，为了简化计算，还可以作如下的假设[10]：

（1）同步发电机的此暂态过程可以忽略；

（2）同步发电机定子回路电阻与输电线路电阻对模型建立的影响极小，可以忽略不计；

（3）忽略转速变化对电磁过程的影响，用恒定阻尼系数D来反映机械阻尼转矩的影响；

（4）励磁机的时间常数Te≈0，系统控制量是发电机的励磁绕组的偏差ΔEf。

由于转子的运动偏差方程为：

励磁绕组的动态偏差方程为：

所以系统状态方程为：

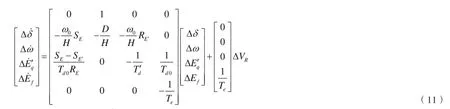
H为转动惯量，由于qE′不便于测量，所以采用机端电压ΔVt来代替qE′，即

又由于在实际系统中采用的是ΔPe、Δω、ΔVt和ΔEf的一组状态量，通过状态变量置换，再结合式（11），可以得到ΔPe、Δω、ΔVt和ΔEf所表示的状态方程：

由于发电机采用可控硅励磁系统，则可以忽略励磁时间常数Te≈0，那么控制量U就是励磁绕组电压ΔEf，系统状态方程可以表示为X.=AX+BU 形式的三阶形式[8][12]：

式（14）即为在单机无穷大系统条件下，最优励磁控制系统的状态空间方程。下面对该状态方程中的相关变量的求解作一阐述。

对于凸极机：

无论是对于凸极机还是隐极机有：

在以上各式中，Vs表示无穷大母线电压，δ称为转子运行角，Td0为定子绕组开路时励磁绕组的时间常数，D为机组的阻尼系数[12-14]。

2.4 7MW线性二次型最优励磁控制系统设计

由线性二次型最优励磁控制系统的数学模型如式（14）知，系数矩阵：

7MW水轮发电机的仿真参数如表1所示：

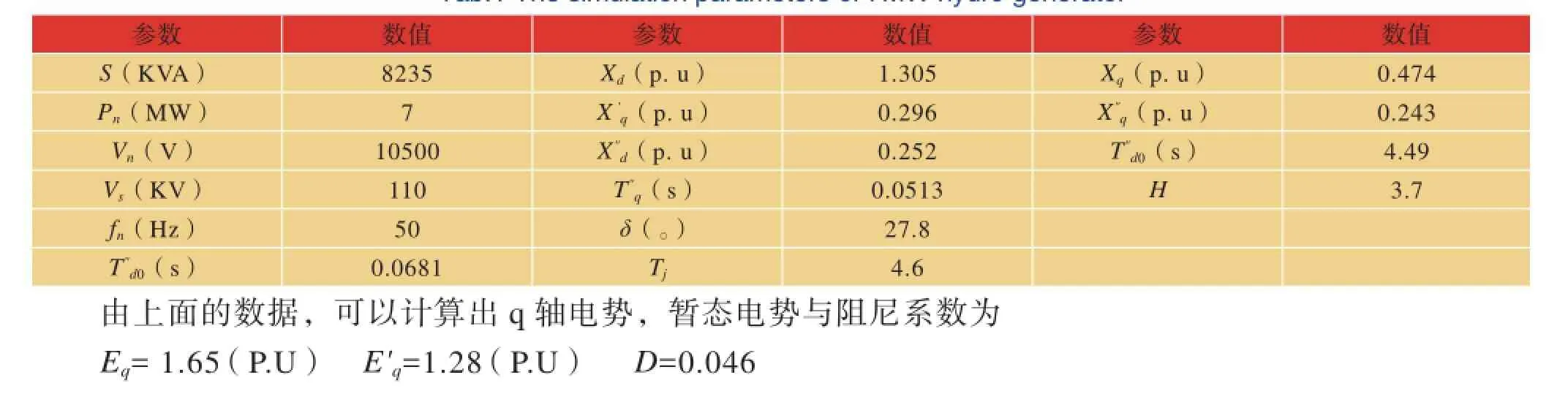
表1 7MW水轮发电机的仿真参数Tab.1 The simulation parameters of 7MW hydro generator

则系数矩阵分别为

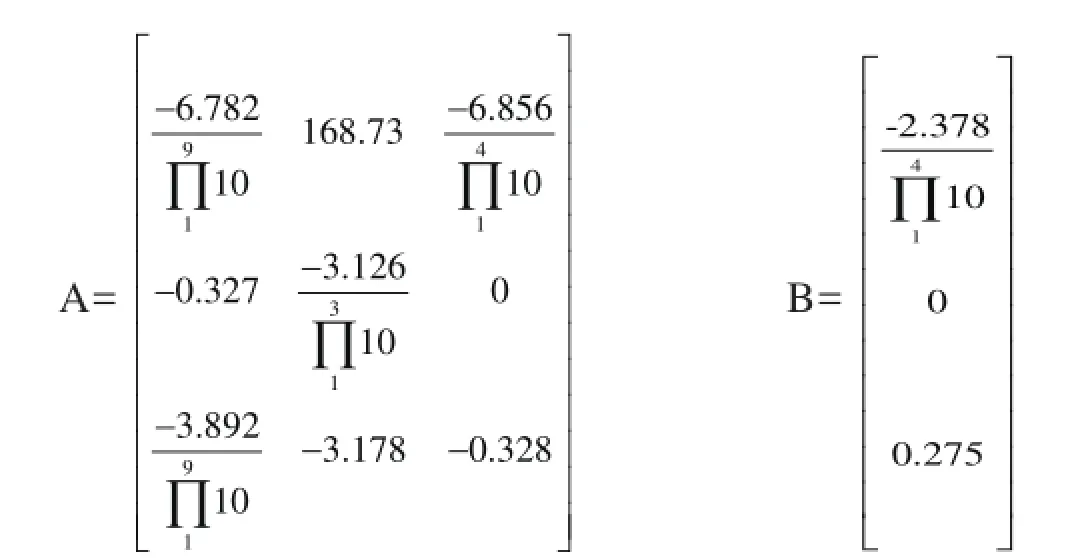
由于D=[B AB A2B]，经计算D的行列式不等于零。根据控制理论，该励磁控制系统完全可控。

3 算例仿真分析

3.1 仿真模型的建立

为了保证所研究的问题具有普遍性，本文仍是采用单机无穷大系统这个模型为基本假设，建立7MW的同步发电机多变量线性最优二次型励磁控制系统的仿真模型如下图5，MATLAB提供的模块有7MW同步发电机（Synchronous Machine）、出口侧升压变压器、励磁调节器（Excitation system）、测量元件等[14-17]。

图4 单机——无穷大系统仿真模型Fig.4 Single - infinity system simulation model

上图4仿真模型中的励磁控制器的内部模型如下图5

同时，为了验证本文设计的线性二次型最优励磁控制器的合理性、正确性。因此与AVR+PSS励磁控制器在静态小扰动和暂态大扰动下的控制效果进行对比。

图5 线性二次型最优励磁系统的控制器Fig.5 The linear quadratic optimal controller of excitation system

3.2 在线性二次型最优励磁控制与AVR+PSS励磁控制下的静态小扰动仿真

由图6与图7可知，在最优控制与AVR+PSS控制两种控制下，施加相同的小扰动，无论是从波动的幅度还是持续波动的时间的角度来看，最优控制下的励磁控制器有绝对的优势，因为它不仅波动的幅度小，而且持续的波动时间也短，对小扰动表现了更强的适应性。

3.3 在线性二次型最优励磁控制与AVR+PSS励磁控制下的暂态大扰动仿真

由图8与图9可知，在线性二次型最优控制与AVR+PSS控制两种控制下，施加相同的大扰动，无论是从波动的幅度还是持续波动的时间的角度来看，最优控制下的励磁控制器有绝对的优势，因为它不仅波动的幅度小，而且持续波动的时间也短，对大扰动表现了更强的动态特性。

4 结论

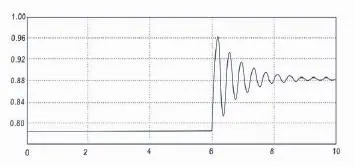
图6 在最优控制下小扰动系统电功率的阶跃响应Fig.6 Small disturbance under the optimal control system of electric power step response

图7 在AVR+PSS励磁控制下小扰动系统电功率的阶跃响应Fig.7 Small disturbance under AVR + PSS excitation controlsystem of electric power step response

图8 在最优控制下大扰动系统电功率的阶跃响应Fig.8 Big disturbance under the optimal control system of electric power step response

图9 在AVR+PSS励磁控制下大扰动系统电功率的阶跃响应Fig.9 Large disturbance under AVR + PSS excitation controlsystem of electric power step response

本文通过利用自并励发电机励磁模型的研究，充分使用最优控制原理以及充分体现设计最优控制的基本步骤，设计了7MW最优自并励励磁控制器。通过对7WM单机无穷大励磁控制系统的仿真，用图形验证了系统的稳定性与可控性，同时，通过在AVR+PSS励磁控制与线性最优励磁控制两种控制下，施加静态小扰动与暂态大扰动的仿真，从图形中可以看出，最优控制系统具有更好的动态特性与良好的阻尼性。正如前文所说，最优控制比AVR+PSS控制方式有更好的适用扰动的能力，具有更好的实际应用价值。

［1］ 李啸骢，谷立基，徐俊华，等. 基于模糊协调控制策略的同步发电机励磁系统研究［J］. 电力系统保护与控制，2011，39（11）：62-66. LI Xiaocong，GU Liji，XU Junhua，et al. Study on the synchronous excitation system based on the strategy of fuzzy coordinated control［J］. Power System Protection and Control，2011，39（11）：62-66.

［2］ 程启明，程尹曼，薛阳，等. 同步发电机励磁控制方法的发展与展望［J］. 电力自动化设备，2012（2）. CHENG Qiming，Cheng Yinman，Xue Yang，et al. Development and outlook of synchronous generator excitation control method ［J］. Electric power automation equipment，2012 （2）.

［3］ 邓超. 同步发电机励磁控制器研究与开发［J］. 2012. Deng chao. Synchronous generator excitation controller of research and development ［J］. 2012.

［4］ 杨慧敏. 区域电网低频振荡特性分析与抑制方法的研究［D］. 武汉：华中科技大学，2009. YANG Huimin. Area of low frequency oscillation characteristics analysis and suppression method research ［D］. Wuhan：huazhong university of science and technology，2009.

［5］ 董宸. 600MW汽轮发电机组励磁系统建模研究［D］. 武汉：华中科技大学，2006. Dong Chen. 600 mw steam turbine generator excitation system modeling research ［D］. Wuhan：huazhong university of science and technology，2006.

［6］ 李东辉. 船舶柴油发电机组的建模与运行仿真研究［D］. 大连：大连海事大学，2011. LI Donghui. Marine diesel generator set runs of modeling and simulation study ［D］. Dalian：dalian maritime university，2011.

［7］ 罗建，冯树辉，蔡明，等. 基于可观测量的同步发电机参数的时域辨识［J］. 电力系统动，2011，35（7）：24-28. LUO Jian，FENG Shuhui，CAI Ming，et al. Time domain parameter identification of synchronous generator based on measurable variables［J］. Automation of Electric Power Systems，2011，35（7）：24-28.

［8］ 孙元章，黎雄，戴和平，等. 同时改善稳定性和电压精度的非线性励磁控制器［J］. 中国电机工学报，2007，27（1）：14-18. SUN Yuanzhang，LI Xiong，DAI He-ping，et al. A nonlinear excitation controller to improve both power system stability and voltage regulation accuracy［J］. Proceedings of the CSEE，2007，27（1）：14-18.

［9］ 杨伟，李仁东. 带电压反馈的非线性最优励磁控制器设计［J］. 电力系统保护与制，2010，38（14）：110-114. YANG Wei，LI Ren-dong. Design of nonlinear optimal excitation controller with voltage feedback［J］. Power System Protection and Control，2010，38（14）：110-114.

［10］ 刘取. 电力系统稳定性及发电机励磁控制［M］. 北京：中国电力出版社，2007：90-95. Liu Qu. Power system stability and generator excitation control ［M］. Beijing：China power press，2007：90-95.

Design of Small Hydropower Self-shunt Excitation Controller Based on the Linear Quadratic Optimal Control

DENG Zhao-jun, LEI Min, ZENG Jin-hui, LI Dan
(College of Electrical and Information Engineering, Hunan University of Technology, Zhuzhou, 412007 China)

Nowadays, the stability of small hydropower generator excitation system has become an important research topic, with the increasing requirement of power quality and power demand. Aiming to improve the stability of small hydropower generator excitation system， this paper established the state equation of a single machine infinite bus system and designed a linear quadratic type 7MW optimal self-shunt excitation controller with feedback of machine terminal voltage, the angular velocity and active power， under the linear quadratic optimal control theory. In the single-machine infinite system， using MATLAB simulation software simulates large and small two disturbances numerical example and compared AVR + PSS. The simulation results show that the optimal controller has better damping and dynamic, and it has a certain practical application value.

Linear quadratic; Optimal control; Self-shunt excitation controller

10.3969/j.issn.2095-6649.2016.02.003

DENG Zhao-jun, LEI Min, ZENG Jin-hui, et al. Design of Small Hydropower Self-shunt Excitation Controller Based on the Linear Quadratic Optimal Control［J］. The Journal of New Industrialization， 2016， 6（2）: 13-20,26.

湖南省自然科学基金项目（2016JJ5038）；湖南省研究生科研创新基金资助项目（CX2015B563）

邓昭俊（1987-），男，湖南邵阳人，硕士研究生，主要研究方向：电力网络自动化技术及应用

雷敏（1973-），女，湖南工业大学副教授，博士，研究方向为复杂网络理论及其在电网稳定性分析中的应用等

本文引用格式：邓昭俊，雷敏，曾进辉，等. 基于线性二次型最优控制的小水电自并励励磁控制器设计［J］. 新型工业化，2016，6（2）：13-20，26.