紧凑型轴流式血泵电机的设计与仿真

魏朝富，杨石平

(武汉理工大学机电工程学院，湖北武汉430070)



紧凑型轴流式血泵电机的设计与仿真

魏朝富，杨石平

(武汉理工大学机电工程学院，湖北武汉430070)

针对传统轴流式磁悬浮血泵存在轴向尺寸偏长，不利于植入问题。提出一种将无刷直流电机与径向磁悬浮轴承集成结构，可有效缩短血泵轴向尺寸；在讨论血泵结构的基础上，重点通过对无轴承直流电机进行理论计算，获得其设计参数，然后采用数值仿真，讨论了电流、位移以及转子位置角对无轴承直流电机径向悬浮力的影响关系。

轴流式血泵 无轴承电机 径向悬浮力 数值仿真

0 引言

目前血泵因心脑血管疾病高发得到广泛研究[1]。对于轴流式血泵，其轴向长度过长会使得血泵不利于植入人体，并且加大了血液流经血泵的路程，从而增大对血细胞的破坏作用。本文以减小血泵轴向长度过长为目的，提出将无轴承无刷直流电机应用于轴流式血泵，无轴承无刷直流电机可有效整合无刷直流电机和径向电磁轴承[2-3]，从而大大缩短轴流式磁悬浮血泵轴向长度。对无轴承无刷直流电机的研究，日本学者Masahide Ooshima是其中的代表[4-5]。近年来国内江苏大学陈雷刚等人建立无轴承无刷直流电机径向悬浮力的数学模型[6]，刘贤兴等人通过有限元分析无轴承无刷直流电机的电磁性能[7]，朱熀秋等人设计了一种新型的无轴承无刷直流电机的控制策略[8]。本文将对电流、位移以及转子位置角对无轴承无刷直流电机径向悬浮力的影响关系进行研究。

1 紧凑型轴流式磁悬浮血泵设计

图1展示了采用无轴承无刷直流电机作为支撑和驱动结构的紧凑型轴流式血泵的结构。其由定子部分、转子部分以及壳体部分组成，血液流经血泵流道时在高速旋转的转子叶轮驱动下向前推进，从而使得该血泵达到辅助心脏泵血的作用。

对于血泵的转子，其轴向自由度由两组锥形永磁轴承约束，并且由于血泵的驱动装置和磁悬浮支撑装置被整合，其轴向长度得到缩短。相较于径向电磁轴承，无轴承无刷直流电机没有结构限制，其对转子施加的悬浮力可在转子全长范围内产生，则在转子的轴向长度较短的情况下，将无轴承无刷直流电机轴向长度加长，由于锥形永磁轴承对转子所施加的约束作用以及定子对转子所施加的径向悬浮力均布于转子，在此仅用一个无轴承无刷直流电机径向支撑转子并且给转子提供转矩。

图2 无轴承永磁无刷直流电机结构图

图2为无轴承无刷直流电机的原理示意图，其由一个12槽的定子铁芯和一个表面嵌入4极永磁体的内转子组成。定子铁芯上嵌入两组绕组，一组给转子提供悬浮力，另一组给转子提供转矩。转矩绕组采用三相星形连接，其中A1、A2、A3、A4四个线圈串联成A相绕组，B1、B2、B3、B4四个线圈串联成B相绕组，C1、C2、C3、C4四个线圈串联成C相绕组。同时，a1和a2、b1和b2、c1和c2三套即六对绕组组成悬浮力绕组，因此可产生六个方向的悬浮力，每对绕组又由对称的两个线圈串联而成，如图中的a11、a12串联成a1，a21、a22串联成a2，其它的亦是如此。

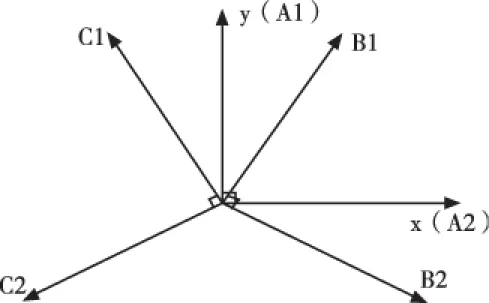
图3 悬浮力生成相位坐标示意图

当上述任意一对绕组通电后，便会打破气隙中的磁场平衡，从而产生一个电磁拉力。转矩绕组为三相两通六状态，因此任意时刻转矩绕组不通电的那一相的四个定子齿上的悬浮绕组通电产生径向悬浮力，因此同齿的悬浮绕组和转矩绕组不同时通电，二者之间的耦合很小，更有利于控制。每组悬浮绕组可以产生两个垂直方向的径向悬浮力，故可合成平面内任意方向的力来平衡转子偏移，每组悬浮绕组产生悬浮力可通过旋转坐标系来进行相位之间的联系，根据图2中各个悬浮绕组位置可得到三对悬浮绕组产生悬浮力的相位坐标图(图3)。

2 无轴承无刷直流电机结构设计

作用在转子上的力包括了三个部分：

1)永磁体在气隙产生的永磁磁场和悬浮绕组通电产生的电磁磁场相互作用产生的电磁拉力。

2)转子偏心在永磁磁场作用下产生的偏移磁拉力。

3)转子所受的重力。

其中1)和2)的合力便是电机提供的悬浮力。因此要使得无轴承无刷直流电机的转子可以悬浮起来，悬浮绕组设计的原则是：悬浮力=电磁拉力+最大偏移磁拉力≥转子重力。可以此设计原则为思想来计算悬浮绕组的相关参数。

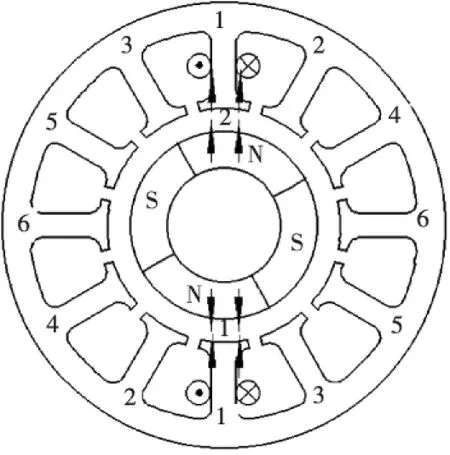
图4 单对绕组导通磁场方向

如图2所示，重力方向为垂直向下即图示1齿方向，因此当转子向下有个最大偏移量时，所需产生的悬浮力最大。悬浮绕组a1导通，悬浮绕组a1是由绕组a11和a12串联而成，假设转子向下的偏心位移为x，绕组中通入图4所示方向的电流i，气隙减小处1电磁线圈与永磁体产生的磁场相互抵消，气隙增大处2电磁线圈与永磁体产生的磁场相互叠加。为了方便计算，将磁路做对称处理，以两个气隙处磁场为分析对象,计算1齿方向受力情况。

设定参数：hm—永磁体的厚度，la—转子轴向长度，α—平均气隙长度，N—线圈a11和a12的匝数，x—转子向下偏心的位移，i—绕组中通过的电流，m—转子质量，Sa—磁路有效磁通面积，μ0—真空磁导率，μr—相对磁导率，Fm—永磁体磁势。

当转子处于中间位置时，即x=0，永磁体和定子之间的偏移磁拉力为0，计算电磁拉力为：

(1)

对于图2，由于上式计算为偏移方向的那两个齿1对转子的偏移磁拉力，与偏移方向垂直的方向没有偏移，磁拉力合力为0，如图4所示永磁体位置，齿3和齿4不走磁路，亦不对转子产生偏移磁拉力，因此竖直方向上的偏移磁拉力的合力为齿1、2、5对转子作用的合力。考虑电流i=0，分析几何关系有偏移磁拉力的合力为齿1偏移磁拉力的2倍：

Fx=Fx1(1+cos230°+cos260°)

(2)

由上述结果可知，电磁拉力与偏移磁拉力的符号相反，即方向是相反的：悬浮力=电磁拉力+最大偏移磁拉力≥转子重力。则有：

Fi≥|Fx|+mg

(3)

定子铁芯的外径40 mm，内径20 mm；转子外径15.8 mm，内径5 mm。单边流道腔的间隙2.1 mm，转子重量0.031 kg，转子启动前处于最低点，转子中心偏心距离0.2 mm，根据式(3)设计原则，设计无轴承无刷直流电机的结构参数如表1所示。

表1 无轴承无刷直流电机相关结构尺寸参数

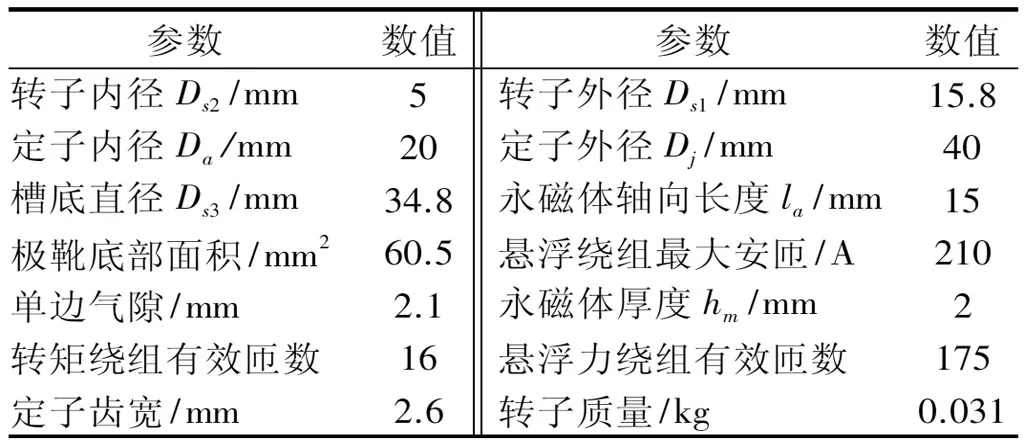
参数数值参数数值转子内径Ds2/mm5转子外径Ds1/mm15.8定子内径Da/mm20定子外径Dj/mm40槽底直径Ds3/mm34.8永磁体轴向长度la/mm15极靴底部面积/mm260.5悬浮绕组最大安匝/A210单边气隙/mm2.1永磁体厚度hm/mm2转矩绕组有效匝数16悬浮力绕组有效匝数175定子齿宽/mm2.6转子质量/kg0.031

按照设计数据可知，通过式(1)计算电磁拉力为：

Fi=3.849 N

通过式(2)可以求得最大偏移磁拉力为：

Fx=-3.456 N

重力为0.31 N，因此表1数据满足式(3)的要求。

3 无轴承无刷直流电机的仿真分析

本文在ANSYS中建立该无轴承无刷直流电机的有限元模型，图5为线圈不通电流时的磁通密度分布和单对线圈通电2 A后磁通密度分布云图。

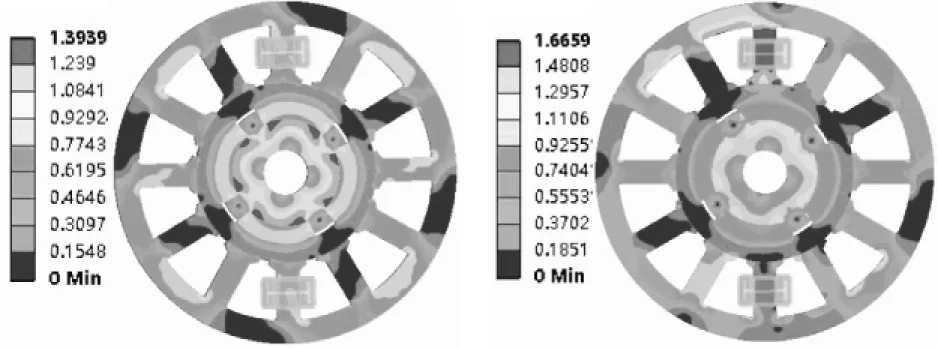
(a)线圈电流为0 A (b)线圈电流为2 A图5 无轴承无刷直流电机磁场分布云图

图7 偏移磁拉力与转子中心偏移量的关系

图6与图7分别为单套悬浮线圈导通后电流对转子产生的电磁拉力以及转子偏心后偏移量对偏移磁拉力的仿真结果。由图可知电流对力和偏移量对力均呈良好的线性关系，这与计算结果也是比较吻合的。

由表1设计最大安匝电流与设计悬浮绕组匝数可知，设计线圈最大电流为1.2 A，由图6可知电磁拉力仿真值为4.3 N，由图7可知当最大偏移为0.2 mm时有最大偏移磁拉力为2.65 N，因此仿真结果也满足式(3)的要求。通过图6数据比较可知，上述计算过程中，电磁拉力计算值小于仿真值，偏移磁拉力计算值大于仿真值，但相差都不是特别大，因此只要计算值满足式(3)要求，仿真值亦满足。

上文仿真计算的转子处于某一位置时的结果，因此需验证不同转子位置角下设计过程是否合理。由无轴承直流电机的原理可知，某一对悬浮绕组的通电间隔为30°的转子位置角，因此需考虑转子位置对悬浮力的影响，验证悬浮力在运动过程是否满足式(3)。如图8所示从永磁体的一边边线正对齿的中心线开始作为0°起点，每5°一个间隔，线圈电流为1A，仿真线圈产生的电磁拉力随转子位置角的变化的关系，结果如图9和图10所示。

图10 x向电磁拉力随转子位置角之间的关系

根据图9，转子位置角的改变会使得y向电磁拉力发生改变，当转子位置角为35°时，定子齿正对永磁体中心，这时悬浮绕组通电产生电磁拉力最大，且以 35°为中心两边成对称。当处于20°到50°之间时，电磁拉力处于3.5 N到4 N之间，由前面公式计算得其计算值为3.2 N，因此转子旋转过程中也可保证有足够转子位置角段为通电区间提供足够电磁拉力。由图10，转子位置角的改变会产生x向的电磁拉力，两个方向的电磁拉力随转子位置角的改变存在耦合，x向电磁拉力随转子位置角改变呈良好的线性关系。当定子齿正对永磁体中心时x向耦合力为0，因为此时电机定转子处于对称位置。另外，通过仿真还发现转子位置角的改变对偏移磁拉力的影响很小，这也验证了设计计算过程的合理性。

综上所述，可知当定子齿正对永磁体中心时可产生更大的悬浮力且悬浮力比较稳定，耦合力也较小。参考这一结论，结合无轴承无刷直流电机原理，在控制过程中应该选择图8所示的20°到50°这一转子位置段作为该绕组的通电间隔。

4 结束语

本文设计了一种应用无轴承无刷直流电机的紧凑型轴流式血泵结构，这种结构可有效减小血泵轴向长度过长带来的不利影响。通过对无轴承无刷直流电机的研究，给出其结构设计计算方法与过程，通过ANSYS软件建立无轴承无刷直流电机的有限元模型，验证了设计计算过程的合理性，通过仿真得到电磁拉力随转子位置角改变的关系以及两个方向悬浮力的耦合关系。此外悬浮绕组一个通电间隔内，应使得通电定子齿尽可能正对永磁体的中心，这样有利于产生稳定的悬浮力，并且两个方向的径向悬浮力耦合也较小。

[1] 郭龙辉.第三代血泵的研究进展[J].中国胸心血管外科临床杂志, 2010,17(4): 321-325.

[2] 刘奕辰, 朱熀秋. 无轴承无刷直流电机研究现状及发展趋势[J]. 微电机, 2014 (8):74-78.

[3] 贾磊, 朱熀秋, 徐亚超. 无轴承无刷直流电动机原理、控制及应用综述[J]. 微电机, 2009, 42(4):62-65.

[4] Ooshima M, Takeuchi C. Magnetic suspension performance of a bearingless brushless DC motor for small liquid pumps[J]. IEEE Transactions on Industry Applications, 2011, 47(1):72-78.

[5] Ooshima M, Rahman M A. Control strategy of magnetic suspension and performances of a bearingless BLDC motor[C]// 2011 IEEE International Electric Machines & Drives Conference (IEMDC). IEEE, 2011:71-76.

[6] 陈雷刚, 朱熀秋. 无轴承无刷直流电机径向悬浮力精确数学模型[J]. 中国电机工程学报, 2012, 32(36):75-81.

[7] 刘贤兴,李慧慧, 李兵伟. 一种新型无轴承无刷直流电机电磁性能的有限元分析[J]. 微电机, 2012, 45(7):15-19.

[8] 朱熀秋，单龙.无轴承无刷直流电机悬浮力新型控制策略[J]. 江苏大学学报(自然科学版), 2015, 36(2):209-214.

Design and simulation of the motor for compact axial-flow blood pump

WEI Chaofu, YANG Shiping

Aiming at the problems of overlength axial size and implantation difficulty of the traditional axial-flow maglev blood pump, we designed an integrated structure with BLDC and radial maglev bearing, which could effectively reduce the axial size of the pump. We analyzed the design parameters of the bearingless motor by theoretical calculation, then carried out numerical simulation to analyze the effects of the electric current, the displacement and the rotor position angle on the radial levitation force of the bearingless motor.

axial-flow blood pump; bearingless motor; radial levitation force; numerical simulation

TM35

A

1002-6886(2016)05-0061-04

魏朝富(1992-)，男，武汉理工大学机电工程学院硕士，主要研究血泵及无轴承电机。

2016-04-10