微重力主动隔振系统电磁作动器设计与仿真
2016-11-16陈作明陈昌皓
陈作明,陈昌皓
(武汉理工大学机电工程学院,湖北武汉430070)
微重力主动隔振系统电磁作动器设计与仿真
陈作明,陈昌皓
(武汉理工大学机电工程学院,湖北武汉430070)
为满足空间科学实验载荷对微重力环境的要求,需应用隔振系统对实验载荷进行振动抑制。由于被动隔振仅在特定频率范围有效,低频振动抑制必须采用主动隔振手段。在主动隔振的若干种作动器中,电磁作动器以电气传动、非接触、响应速度快和允许偏移大等特点适用于微重力主动隔振系统。本文设计了一种基于洛伦兹力原理的电磁作动器,并利用有限元软件ANSYS Workbench对作动器特性进行仿真,了解作用力与电流和位移的关系。
微重力 主动隔振 洛伦兹力 作动器 仿真
0 引言
太空环境为微重力环境下的各类科学实验提供了绝佳的实验条件,然而通过对空间微重力环境的典型评估发现,由于航天器姿态调整,设备运转和人员运动等影响,加速度环境超出了许多对振动敏感实验的需求[1-2]。图1[3]绘制了各类微重力科学实验对环境的要求以及典型空间站环境评估值,可以看出典型空间站环境评估值在0.01 Hz~100 Hz频段的大部分超出了实验载荷对空间站环境的要求,因此需要在科学实验载荷与飞船之间设置微重力隔振系统。
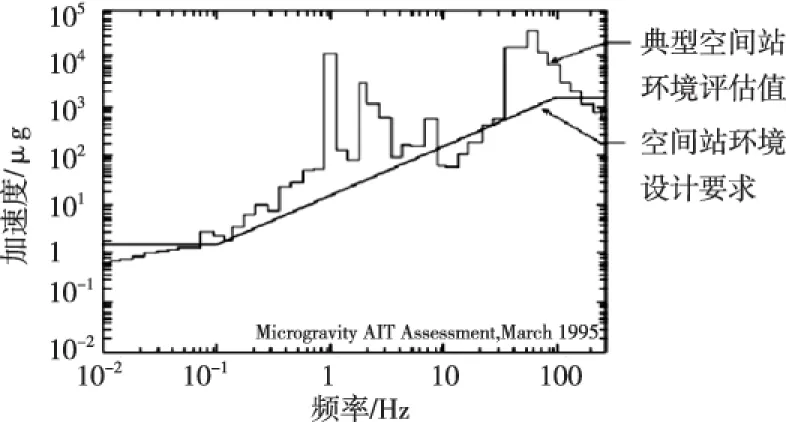
图1 空间站典型微重力环境

1 作动器原理与结构介绍
1.1 作动器基本原理
作动器是主动隔振系统的关键部件,一般安装在隔振对象和振动来源中间,并通过产生可控的作用力对隔振对象过高的加速度水平进行衰减。现有作动器主要有电磁作动器、气/液压作动器、磁致伸缩合金作动器、电致伸缩陶瓷作动器等[6]。其中电磁作动器以电气传动、无需介质、非接触、响应速度快和允许偏移大等特点较适用于微重力环境下实验载荷的振动抑制。
电磁作动器设计原理主要基于电磁力原理和洛伦兹力原理,其基本原理图如图2[7]所示。电磁力原理是指由变化的电流产生可控磁场,该磁场对置于其中的导磁材料产生作用力。洛伦兹力原理是由永磁体或电磁铁产生稳定磁场,该磁场对置于其中的通电导线产生作用力,其计算公式为F=nBIL,其中F为线圈在磁场中的受力,在此可视为作动器作用力,n为线圈匝数,B为导线所处磁场的磁感应强度大小,L则是在磁场中的导线长度。由于基于电磁力原理设计的作动器作用力方向不可改变,且作用力与电流和位移均为非线性关系,不适用于微重力主动隔振系统,因此本文设计的作动器基于洛伦兹力原理。
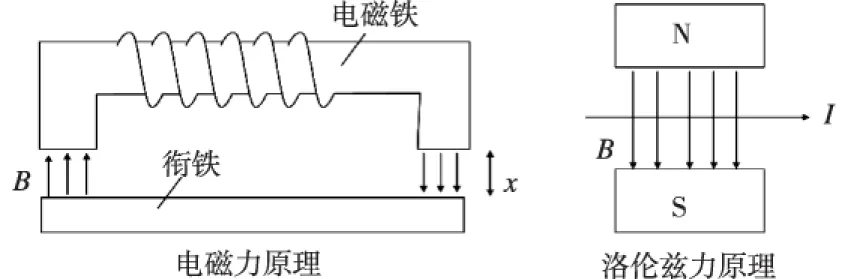
图2 电磁作动器原理图
1.2 作动器设计
根据作动器的应用场景和相关指标,基于洛伦兹力原理设计电磁作动器,其示意图如图3所示,该作动器主要由永磁回路和线圈两部分构成。永磁回路包括磁轭和永磁体,线圈缠绕方法参考双D型缠绕法[8],采用双O型缠绕方法,该方法可以保证位于磁场中的导线电流方向相同且无效线圈处于有效磁场外。永磁回路部分采用自退磁效应设计[9]并基于有限元软件优化,作动器相关参数列于表1中。

表1 作动器参数表
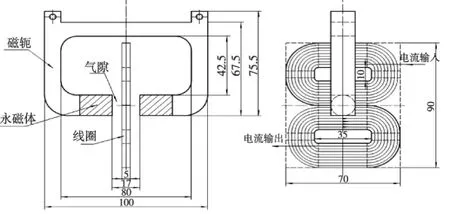
图3 基于洛伦兹力的电磁作动器示意图
2 作动器仿真
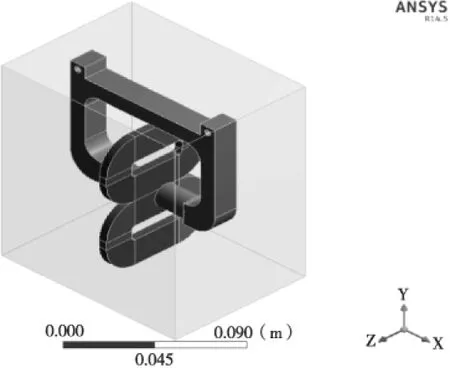
图4 仿真模型
利用ANSYS Workbench软件对作动器的特性进行仿真分析。建立模型如图3所示,在仿真过程中,磁轭部分为固定不动,线圈可自由移动,线圈中心移动的坐标原点位置为永磁回路气隙正中心。坐标轴方向与图4中所示坐标系相同。线圈在x、y、z三个坐标轴方向的受力记为Fx,Fy,Fz。其中Fy为作动器主要作用力,Fx和Fz则是线圈所受到的干扰力。
2.1 电流与作用力的关系
在仿真过程中保持线圈位置固定, 改变线圈通电电流,获得不同电流输入下作动器的作用力。分别将线圈中心固定于坐标(0,0,0)和(5,5,5)两处,获得对应的作用力绘制成折线图如图5和图6所示。

从图5可以看出,当线圈坐标为(0,0,0)时,线圈所受的干扰力接近为零,作动器作用力Fy与线圈通电电流成线性关系。从图6可以看出,当线圈坐标为(5,5,5)并且通以电流时,线圈所受的干扰力Fx和Fz均不为零,电流在0到2.5 A范围时,线圈受到的三个方向的力与电流均成线性关系。当线圈通电电流为1.6 A时,线圈受力Fx=0.246 N,Fy=4.17 N,Fz=-0.099 N。结果表明,当在线圈所受各方向的力均存在时,各方向的力与电流均成线性关系,该结论与理论一致。
2.2 位移与作用力的关系
保持线圈通电电流为1.6 A不变,移动线圈,获得线圈位移与作用力的对应数据,由于仿真模型关于y轴与x轴对称,因此仿真位移点坐标为x从0到5,y从-5到5,z从0到5,且间距均为1。采用MATLAB软件绘制数据等高图,并局部加权回归散点平滑法(Lowess)对图形进行平滑处理。图7代表了x为0到5的各平面对应的yz平面的作用力等高图,图中横坐标均为z轴坐标,纵坐标均为y轴坐标,颜色条代表对应点作用力大小。
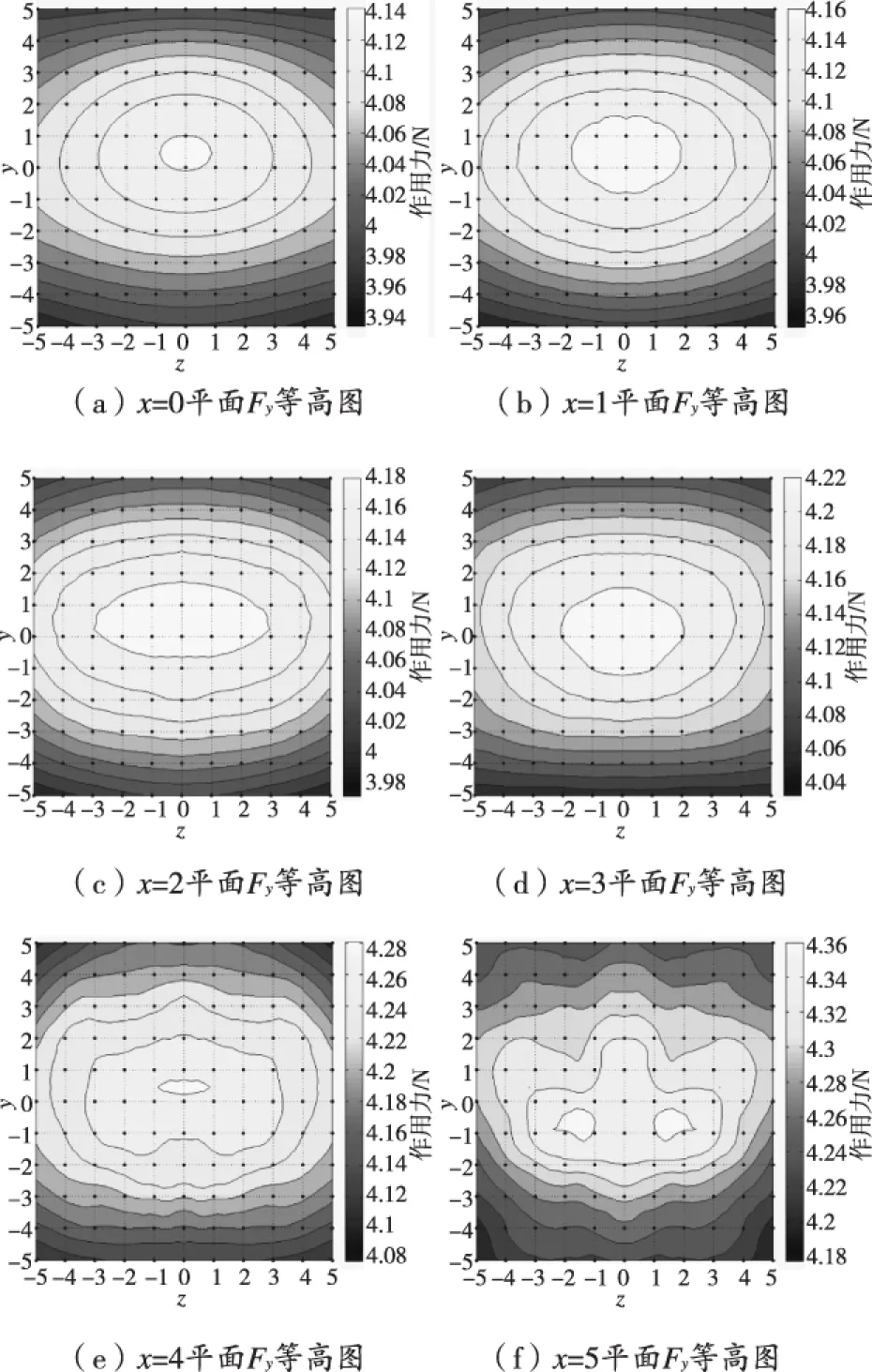
图7 不同平面作用力Fy的等高图
观察图7各图的颜色条可以发现,当x坐标增加时,颜色条数值相应增加。因为当线圈靠近永磁体时,线圈所处磁场增大,作用力也整体相应增大。透过图7(a)到图7(e)可以发现,图形的y轴对称中心约在y=0.5处,即作动器沿y轴移动时,作用力Fy并非关于z轴对称,原因可能为磁轭上下不对称,导致在各个平面x方向磁场中心不在原点处。
图7(a)到图7(d)可近似看成多个同心圆的叠加,等高线之间的间隔近似相等,这意味着在x=0到x=3的这些平面中,作用力Fy与y坐标和z坐标均近似为线性关系。而图7(e)和图7(f)中等高线不再是圆形,且分布变得不均匀,表明当线圈靠近永磁体时,作用力与y坐标和z坐标的线性关系改变。另外,观察各图作用力随着y轴和z轴的变化可以发现,作用力关于y轴变化速率大于关于z轴变化速率,可得出作用力对线圈y轴方向移动更为敏感的结论。
2.3 位移与干扰力的关系
分析模型与仿真结果可以知道,当线圈处于x=0平面时,线圈平面处磁场方向均为x轴方向,干扰力Fx和Fz接近于0,可以忽略不计。而当线圈沿x轴方向移动,线圈所处磁场开始出现沿y轴和z轴方向的分量,伴随着线圈在y轴和z轴方向的移动,这些分量对线圈的受力产生了相应的影响。仿真分析发现在x≠0时,各平面干扰力规律相同,而当x=5时由于最靠近永磁体,干扰力数值较大,规律更加明显,因此选取线圈位于x=5平面时的干扰力绘制成等高图见图8。
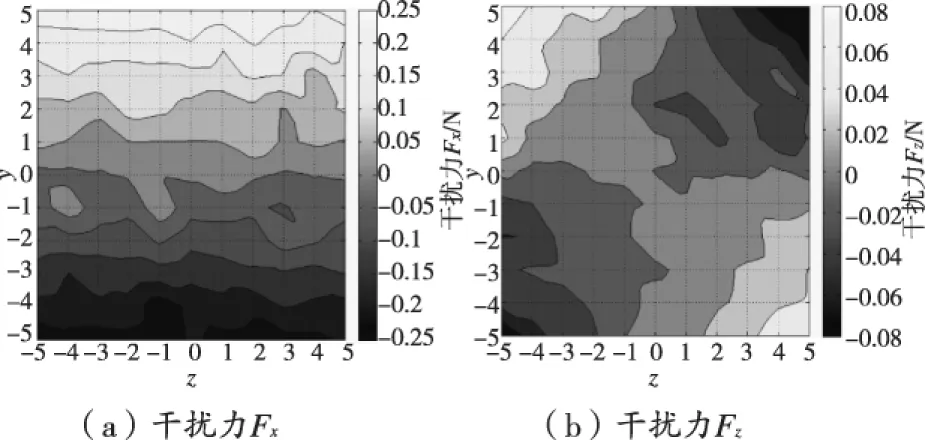
图8 线圈处于x=5平面干扰力等高图
从图8(a)可知,图形在y轴方向有明显层次,当y坐标不变,干扰力Fx基本不随z坐标变化而变化。当y坐标为0时,干扰力Fx为0,当y坐标增加时,Fx相应增加,方向与x轴方向相同,当y坐标减小为负值时,Fx绝对值相应增加,方向与x轴方向相反。
从图8(b)可知,图形可视为关于中心对称,干扰力Fz在y坐标和z坐标绝对值均为5处即图形四个边角处绝对值最大。当y坐标或z坐标有一者为0时,Fz为0。
干扰力的产生原因主要是由于当线圈偏离中心,所在磁场存在y方向与z方向分量,由于在y轴和z轴方向的移动导致线圈各处磁场不对称从而产生了相应的干扰力。通过干扰力的分析对以后作动器的优化设计提供了依据。
3 结论
本文基于洛伦兹力原理设计了一种应用于微重力主动隔振系统的电磁作动器,该作动器主要由永磁回路和线圈构成。运用有限元仿真软件ANSYS Workbench对作动器的特性进行了仿真,获得电流与作用力、干扰力之间的关系,分析了线圈位移对作动器作用力与干扰力的影响,为了解作动器的特性与后续的优化设计提供了依据。
[1] 薛大同,雷军刚,程玉峰,等.“神舟”号飞船的微重力测量[J].物理,2004,33(05):351-358.
[2] 杨彪,胡添元.空间站微重力环境研究与分析[J].载人航天,2014(02):178-183.
[3] Jackson M, Kim Y, Whorton M. Design and analysis of the g-LIMIT baseline vibration isolation control system[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit. Monterey: AIAA, 2002.
[4] 王晓雷,杨庆俊,郑钢铁.整星主动隔振平台研究[J].宇航学报,2007,28(2):438-441.
[5] 任明章.机械振动的分析与控制以及计算方法[M].北京:机械工业出版社,2011:57-107.
[6] 张磊,付永领,刘永光,何琳.主动隔振技术及其应用与发展[J].机床与液压,2005(2):5-8.
[7] 陈进新,王宇.空间微重力磁悬浮平台激励器研究[J].空间科学学报,2008,28(6):584-591.
[8] Edberg D L, Harduvel J T, Schenck D J. Non-contacting isolated stabilized microgravity platform system: US 5638303 A [P].1997-06-10.
[9] 林其壬,赵佑民.磁路设计原理[M].北京:机械工业出版社,1987:154-178,361-408.
Design and simulation of the electromagnetic actuator for the active vibration isolation system under microgravity
CHEN Zuoming, CHEN Changhao
To meet the microgravity environment requirement of spatial scientific experiments, vibration isolation systems are needed to reduce the vibration of the experimental load. Since passive isolation systems are only useful within certain frequency range, active isolation systems are required to provide vibration suppression at low frequencies. Electromagnetic actuator is suitable for the active vibration isolation system under microgravity because of its advantages of electric driving, non-contact, quick response and large allowable displacement. In this article, we designed an electromagnetic actuator based on Lorentz force principle, and carried out simulation with ANSYS Workbench to analyze the relationship between the acting force, the electric current and the displacement.
microgravity,active vibration isolation,Lorentz force,actuator,simulation
TH703; TB535
A
1002-6886(2016)05-0038-04
陈作明,男,武汉理工大学在读研究生,主要从事主动隔振相关研究工作。
2016-04-14
