HRB500钢筋混凝土梁静动态受弯承载力试验研究

李　磊，何　翔，孙　敖，王世合，高　杰

（1.61489部队，河南 洛阳 471023；2.河南省特种防护材料重点实验室，河南 洛阳 471023）

HRB500钢筋混凝土梁静动态受弯承载力试验研究

李磊1，2，何翔1，2，孙敖1，王世合1，2，高杰1

（1.61489部队，河南 洛阳 471023；2.河南省特种防护材料重点实验室，河南 洛阳 471023）

为研究HRB500钢筋混凝土简支梁的受弯承载力，进行7组21根适筋梁的静、动态三分点弯曲加载试验，分别采用0.6%、1.0%两种配筋率，C40、C60两种强度等级的混凝土，3种加载速度，获得梁的截面应变分布曲线，以及开裂载荷、屈服载荷、极限载荷和延性比等参数。通过对比分析试验结果，认为在动态载荷作用下，平截面假定依然成立，梁的开裂载荷可提升1倍以上，屈服载荷和极限载荷有小幅提升。动态屈服载荷可采用静载时的计算方法进行计算，但需要将钢筋和混凝土的静态强度替换为动态强度。梁的延性比基本不受加载速度的影响，配筋率越高的梁延性比越低。

HRB500钢筋；混凝土梁；动态试验；屈服载荷；延性比

0　引　言

HRB500钢筋是一种强度高、韧性好的新型钢筋，在国外的混凝土结构中已得到广泛应用，尤其是在高层建筑、大跨度建筑和抗震等级高的建筑中。我国虽然早在1998年就将HRB500钢筋纳入了GB 1499——1998《钢筋混凝土用热轧带肋钢筋》标准中，但因缺乏相应的钢筋混凝土结构试验资料，直到2010年才将其列入GB 50010——2010《混凝土结构设计规范》［1］。而后国家出台相应政策，在工程领域中大力推广应用HRB500钢筋，近几年其产量得到稳步提升，应用范围正逐步扩展。在军事领域中，军事建筑大量采用钢筋混凝土结构，军事建筑不仅要满足正常的承载力要求，还必须具有一定的抵抗武器打击的能力，而武器对建筑物的作用大部分表现为爆炸、冲击等动态载荷，所以必须对钢筋混凝土结构的动态承载力开展研究，以便为军事建筑的设计建造提供依据。

在动态载荷作用下，钢筋和混凝土等材料的力学行为会发生明显变化［2-5］，材料力学性能的变化必然会影响到钢筋混凝土结构的力学性能，所以应在研究材料动态力学特性的基础上开展钢筋混凝土结构件的动态力学特性研究。钢筋混凝土梁是最常见的结构件，其动态力学性能正逐渐受到国内研究人员的重视。清华大学的陈肈元是国内研究爆炸载荷下钢筋混凝土结构动力性能的开创性学者，其研究成果在最近出版的专著［6］中进行了全面的总结。钱七虎［7］和方秦［8］对防护结构中的钢筋混凝土结构动力性能和设计计算方法进行了更为深入的研究。都浩等［9］和李振宝等［10］分别采用有限元软件对钢筋混凝土梁的动态力学性能进行了数值模拟研究，肖诗云等［11］采用分层纤维模型研究了混凝土的动态特性和钢筋的动态特性对适筋梁和超筋梁的开裂弯矩、开裂曲率、极限弯矩和极限曲率的影响，李敏等［12］对地震作用范围内加载速率对钢筋混凝土梁的影响开展了试验研究与数值模拟。上述研究中涉及到的钢筋都是400MPa级以下的，由于HRB500钢筋列入规范的时间较短，关于HRB500钢筋混凝土梁的动态力学性能研究在国内还未曾见诸报道。笔者利用总参工程兵科研三所的KG400T动载试验机，对HRB500钢筋混凝土梁开展了静态和动态抗弯试验，对其受弯承载力进行了初步分析。

1　试验概况

1.1试件尺寸及载荷预估

本试验的目的是研究动态载荷作用下钢筋混凝土梁的力学响应，试验的加载过程应根据梁的实际承载过程进行简化。动态载荷对结构的作用方式可分为局部作用和整体作用，如果动态载荷作用于结构局部，如直接撞击、接触爆炸等情况，载荷作用点附近区域材料质点将获得极高的速度，使结构局部范围内产生很大的应力，此时难以精确衡量结构局部应力应变的大小，通常只能宏观地研究结构破坏现象。如果动态载荷作用于结构整体，如远距离爆炸、地震等情况，结构将产生整体变形和内力，结构破坏是由于出现过大的变形、裂缝，甚至整体倒塌，破坏部位一般发生在产生最大内力的地方，此时可以采用动力分析方法对结构的动态响应进行较为准确的分析计算。本试验主要研究动态载荷对钢筋混凝土梁的整体作用，所以参照GB/T 50152——2012《混凝土结构试验方法标准》［13］的方法，选取典型的简支梁三分点集中加载方式模拟梁的整体弯曲，研究梁在静态和动态载荷作用下的受弯承载力，并进行对比分析。

本试验共设计了7组21根试验梁，每组3根梁的试验状态完全相同，以降低试验误差。所有试件尺寸全部相同，长度1 800 mm，支撑跨距1 500 mm，剪跨500 mm，截面尺寸300 mm×150 mm，受拉主筋均为HRB500钢筋，混凝土设计强度等级为C40和C60两种，主筋配筋率为0.6%和1.0%两种，主筋混凝土保护层厚度为25mm，理论计算均为适筋梁。试件的配筋方式见图1，采用两根受拉主筋和两根构造筋，中部纯弯曲段受压区没有构造钢筋，箍筋采用直径6mm的HRB400钢筋，箍筋间距根据受拉主筋屈服时不发生剪切破坏的原则计算选取，试件的实际配筋率及实测钢筋强度见表1。

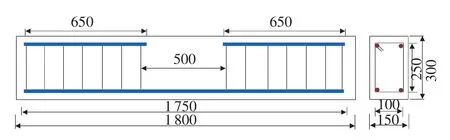
图1　试件配筋示意图（单位：mm）

表1　试件实际配筋率及实测强度

试验梁采用钢模支撑，人工浇筑混凝土，常规浇水养护28天，同时每一根梁分别留存了3个边长150mm的立方体混凝土试块测量立方体抗压强度按照GB/T 50152——2012中的方法，推算混凝土的轴心抗压强度轴心抗拉强度和弹性模量再参照GB/T 50010——2010计算受拉主筋开始屈服时的弯矩和开裂弯矩按照加载方式换算为屈服载荷和开裂载荷计算中所有材料参数均取实测值，试件参数及载荷预估值见表2，表中还列出了试件的实测尺寸和试验速度，其中低速试验是指从加载到试件屈服的时间较长，约为60ms，高速试验是指该时间较短，约为30ms。

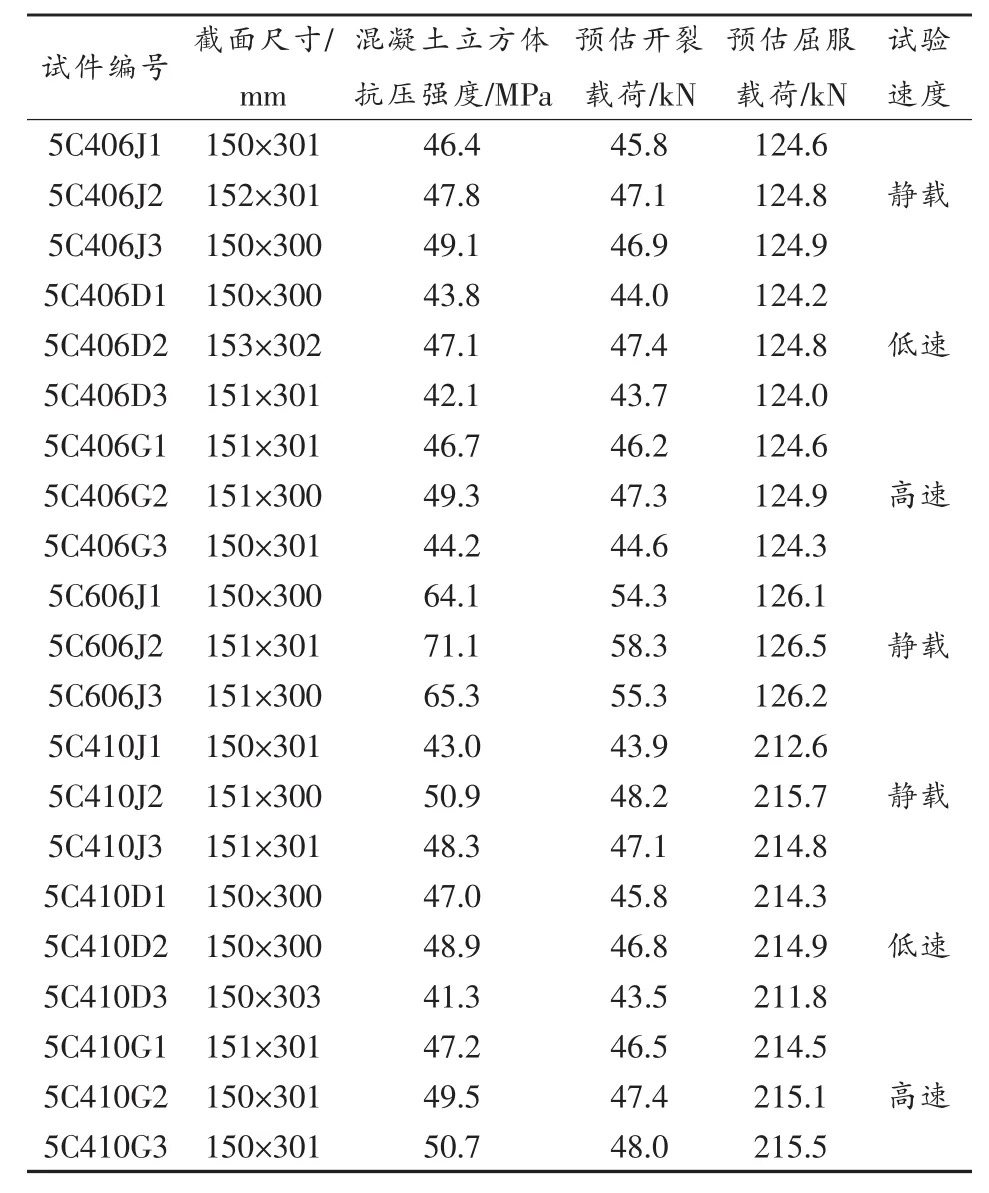
表2　试件参数及载荷预估值

1.2试验方法

本次试验在总参工程兵科研三所的KG400T动载试验机（见图2）上进行，该试验机主要技术指标见表3。该试验机以高压气体作动力，采用气-液联动系统快速产生高压力，使试件获得基本恒定的加载速度，图3为设备的加载原理图。试验前储能器中为高压气体，加载时打开快速阀，气体压力推动活塞快速移动，通过液压油将载荷传递到主缸活塞，主缸活塞对试件施加快速压力，试验中可通过调节阀改变加载速度。

图2　KG-400T动载材料试验机

表3　KG400T动载试验机指标

试验测点布置见图4，混凝土表面应变测点（εc）5个，采用BA120-100AA箔式应变片，在跨中位置从上表面到下表面均匀布置，主要测量混凝土表面应变沿高度的分布情况；钢筋应变测点（εs）4个，采用BF120-5AA箔式应变片，在跨中位置两个主筋上各布置2个应变片，主要测量跨中位置钢筋应变。跨中布置位移传感器（y），量程50mm，测量试件跨中挠度，力传感器（F）固定在分配钢梁上，量程500kN，测量试件承受的总载荷，所有测点均采用东华DH5960超动态信号测试分析系统采集信号。在实际试验中，由于试验机的作动头在下部，固定端在上部，考虑到作动头直接作用于支撑钢梁不利于钢梁稳定和数据测量，可能带来不必要的试验误差，所以采用倒置加载的方法进行试验，将支撑钢梁焊接固定在试验机上部，分配钢梁放置于试件下部，作动头从底部向上加载。由于试验机主活塞行程只有25mm，为了充分加载，在静载试验中采用手动千斤顶加载，动载试验中采用试验机作动头加载。

图3　快速加载原理图

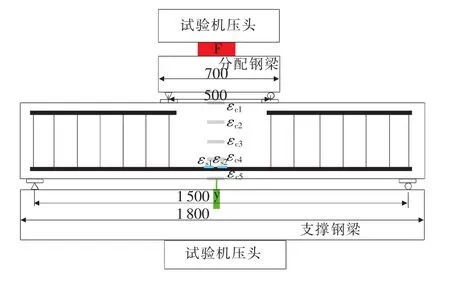
图4　测点布置位置（单位：mm）

静载试验的加载程序参考GB/T 50152——2012确定，试件屈服前按照载荷分级加载，试件屈服后按照跨中挠度增量控制加载。动载试验采用连续快速加载方法，试件直接加载到作动头的最大行程，加载速度由设备中的调节阀控制，分别进行低速和高速两种速度的动载试验。

2　试验结果与分析

2.1试验现象

试验中设计的试件均为适筋梁，静载试验的试验过程可分为以下3个阶段：

1）开裂前阶段。开始加载时，试件受力在弹性范围内，截面尚未开裂，整体变形较均匀，载荷-挠度曲线接近直线变化，试件中性轴位于高度方向的中线上。

2）带裂缝工作阶段。当加载到试件开裂载荷时，在试件跨中或加载点对应位置受拉混凝土表面出现一条或多条垂直裂缝，载荷-挠度曲线上出现第1个明显的转折点，由于裂缝的出现，受拉区混凝土退出工作，其开裂前承担的拉力将转移给钢筋承担，因而裂缝附近的钢筋应变突然增加。随着载荷的继续增大，混凝土裂缝宽度不断增大并缓慢向受压区延伸，同时纯弯段还有新裂缝出现，载荷-挠度曲线的斜率比开裂前有明显降低，曲线斜率随载荷增长有幅度很小的降低趋势，试件中性轴逐步向受压区移动。

3）破坏阶段。当钢筋应力达到屈服强度时，受压区混凝土一般尚未压坏，载荷-挠度曲线上出现第2个明显的转折点。此转折点之后，钢筋进入塑性受力阶段，试件承受的载荷缓慢增长但挠度增长迅速，载荷-挠度曲线变为接近水平的曲线，纯弯段混凝土裂缝宽度增长较快，裂缝深度增长较慢，裂缝深度一般均超过梁高度的3/4，试件中性轴进一步向受压区移动，同时受剪截面出现剪切斜裂缝并不断增长。随着载荷的进一步增大，受压区混凝土出现水平裂缝，并开始剥落、掉块，试件承受的载荷在达到峰值后开始下降，最终受压区混凝土被压溃，出现较为剧烈的碎裂声音，实验结束。

动载试验为瞬时加载，试验机作动头一次加载到最大行程，低速试验的总加载时间为150～200ms，试件屈服的时间为50～70 ms，高速试验的加载时间为70～100ms，试件屈服的时间为20～30 ms，加载完成后保持压力10min。受到试验机作动头的行程所限，难以加载到受压区混凝土破坏，仅有部分试件的受压区混凝土开裂掉块。图5给出了5C406组部分试件的载荷-挠度曲线，从图中可以看出，动载试验的载荷-挠度曲线与静载试验的曲线相似，但是屈服载荷有了明显的提升。

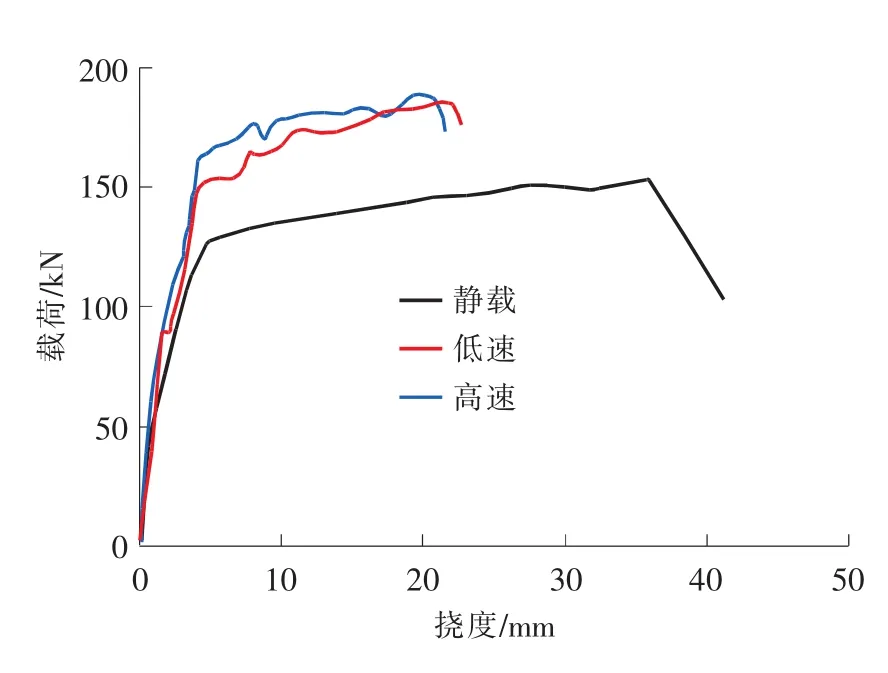
图5　5C406组部分试件的载荷-挠度曲线

2.2试验结果

1）截面应变分布

平截面假定是目前混凝土结构设计规范中受弯构件计算方法的基础，已有很多学者通过静载试验进行了验证，但在动载情况下该假定是否依然成立，需要通过动态试验来验证。本次试验通过沿梁高度方向均布的混凝土应变片测得截面的应变分布情况，可验证在静态和动态载荷作用下平截面假定是否成立。试验中不论静载还是动载试验，部分试件的截面应变分布与平截面假定吻合良好，如图6中给出的5C406J1、5C406G3试件；还有一部分试件的截面应变分布明显与平截面假定不符，如图6中给出的5C606J2、5C406D1试件。出现这种差异的原因在于，混凝土应变片布置与跨中，长度为100mm，当混凝土开裂后，如果裂缝穿过应变片，则应变片测得的为钢筋与混凝土的平均应变，由于混凝土性能的离散性，裂缝在纯弯段出现的位置具有一定的随机性，100mm的范围内并不是一定有裂缝出现，如果应变片在两条裂缝中间，那么应变片测得的为表面混凝土的应变，而两条裂缝中间的混凝土会产生回缩，因而出现了不同的应变分布图。平截面假定是针对整个截面的平均应变而言的，所以应变片在两条裂缝中间的情况应为无效数据。本次试验测得的大部分应变分布情况均基本符合平截面假定，所以在动载情况下平截面假定依然适用。

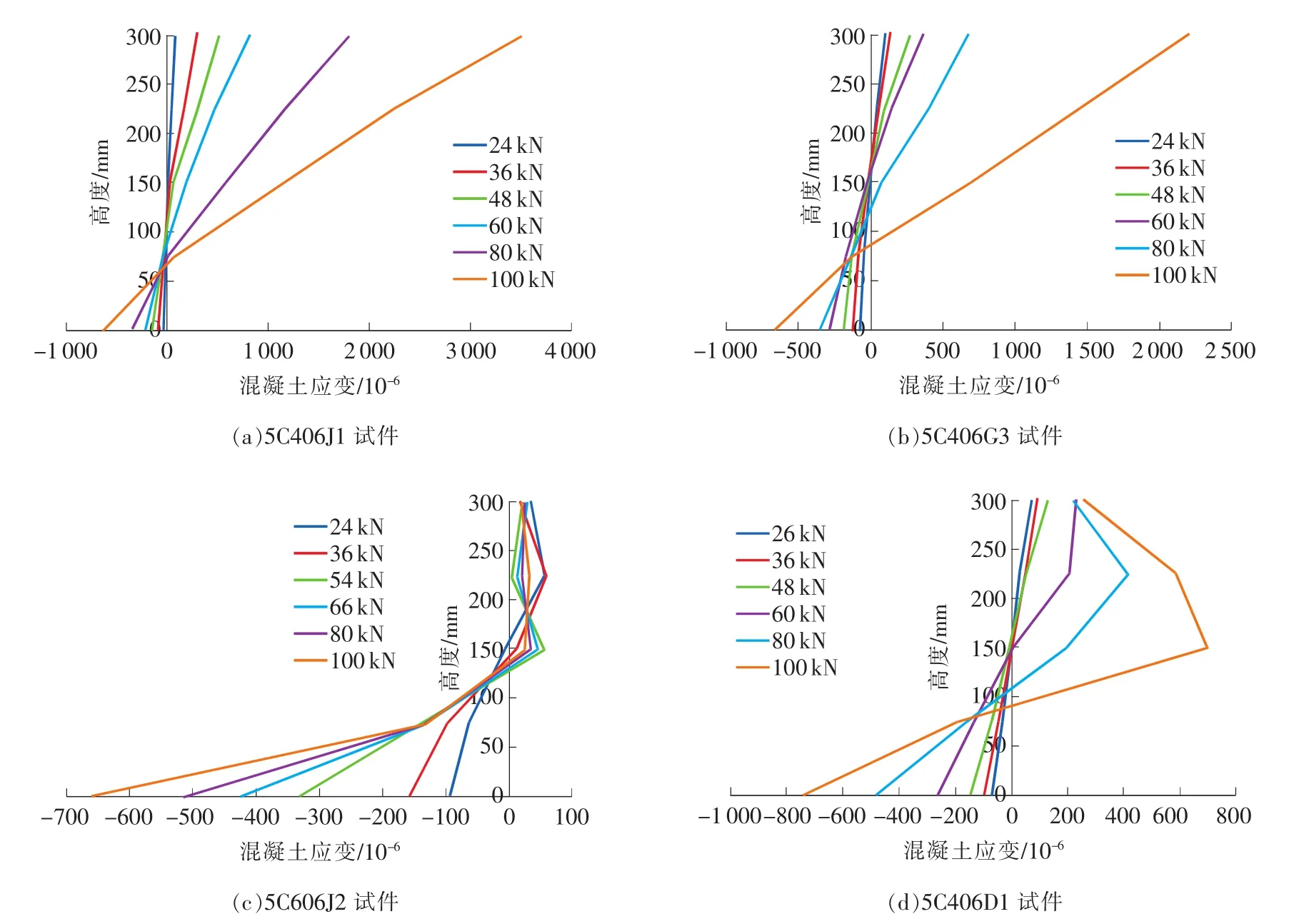
图6　截面应变分布图

2）开裂载荷和屈服载荷

静载试验中依据试验标准和实时观察的试验现象可判断开裂载荷F0cr和屈服载荷Fy0，动载试验的加载过程难以进行实时观察，所以开裂载荷和屈服载荷只能通过试验曲线来判读。图7给出了5C410D3试件的载荷-挠度曲线和载荷-钢筋应变曲线，从图中可观察到较为明显的拐点，如试件开裂时载荷-钢筋应变曲线中的拐点，钢筋屈服时载荷-挠度曲线中的拐点，以这些拐点为依据综合判读试件的开裂载荷和屈服载荷。

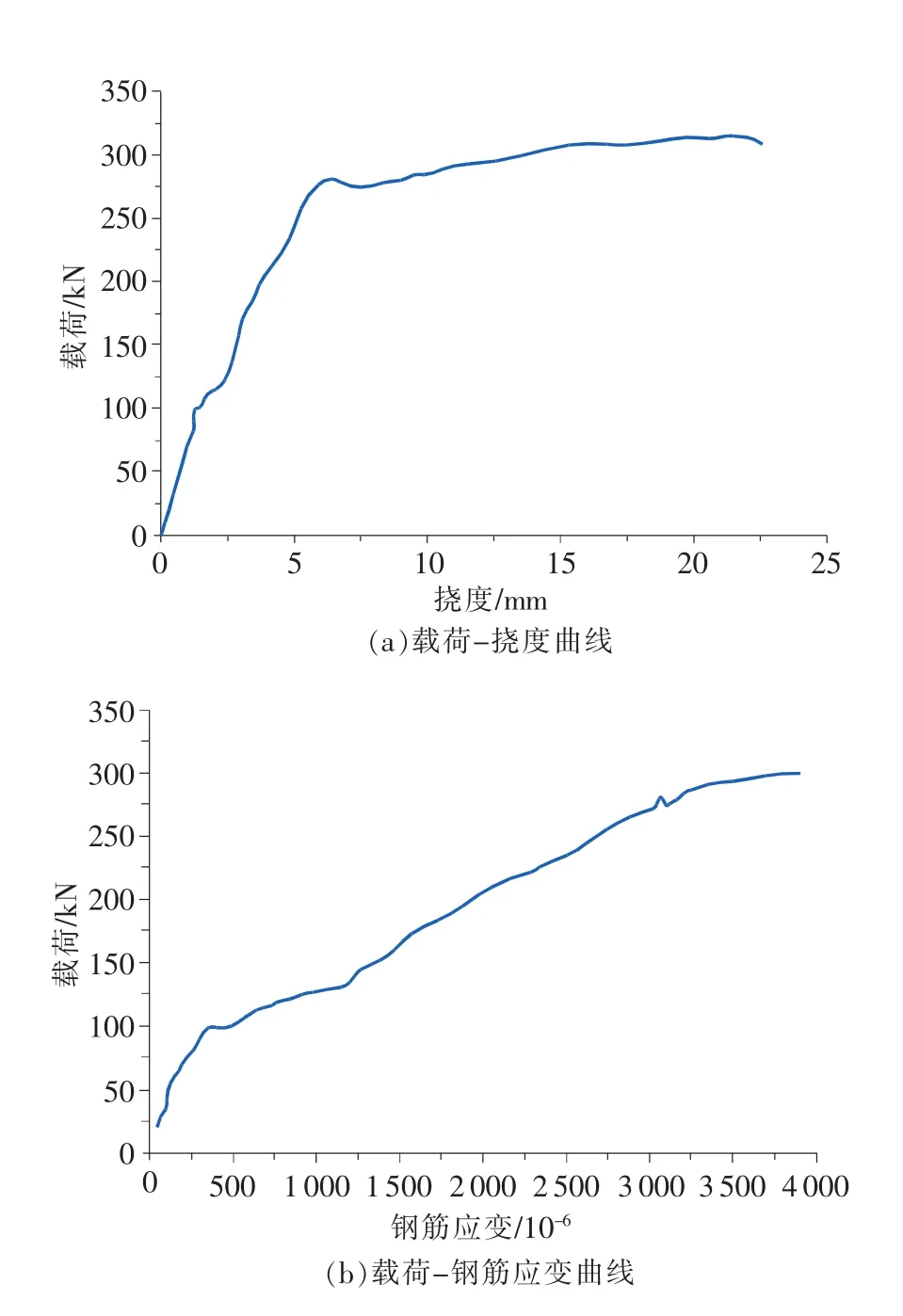
图7　5C410D3试验曲线

3）极限载荷与延性比

极限载荷Fu0为整个试验过程中试件能够承受的最大载荷，一般对应受压区混凝土剥落和崩裂。但动载试验中受试验机行程所限，大部分试件未出现受压区混凝土剥落和崩裂，这里以测得的最大载荷作为极限载荷，实际的极限载荷肯定高于该数值。试件的延性比β为极限载荷下试件的挠度fu0与屈服载荷下的挠度fy0比值，这一数值可反映试件的塑性变形能力。所有试件的试验结果列于表4，其中ts为试验开始加载到试件屈服的时间，5C406J1试件因加载前已有裂缝，其开裂载荷没有测得。5C410D1、5C410D2和5C410G3加载完成后受压区混凝土破裂。

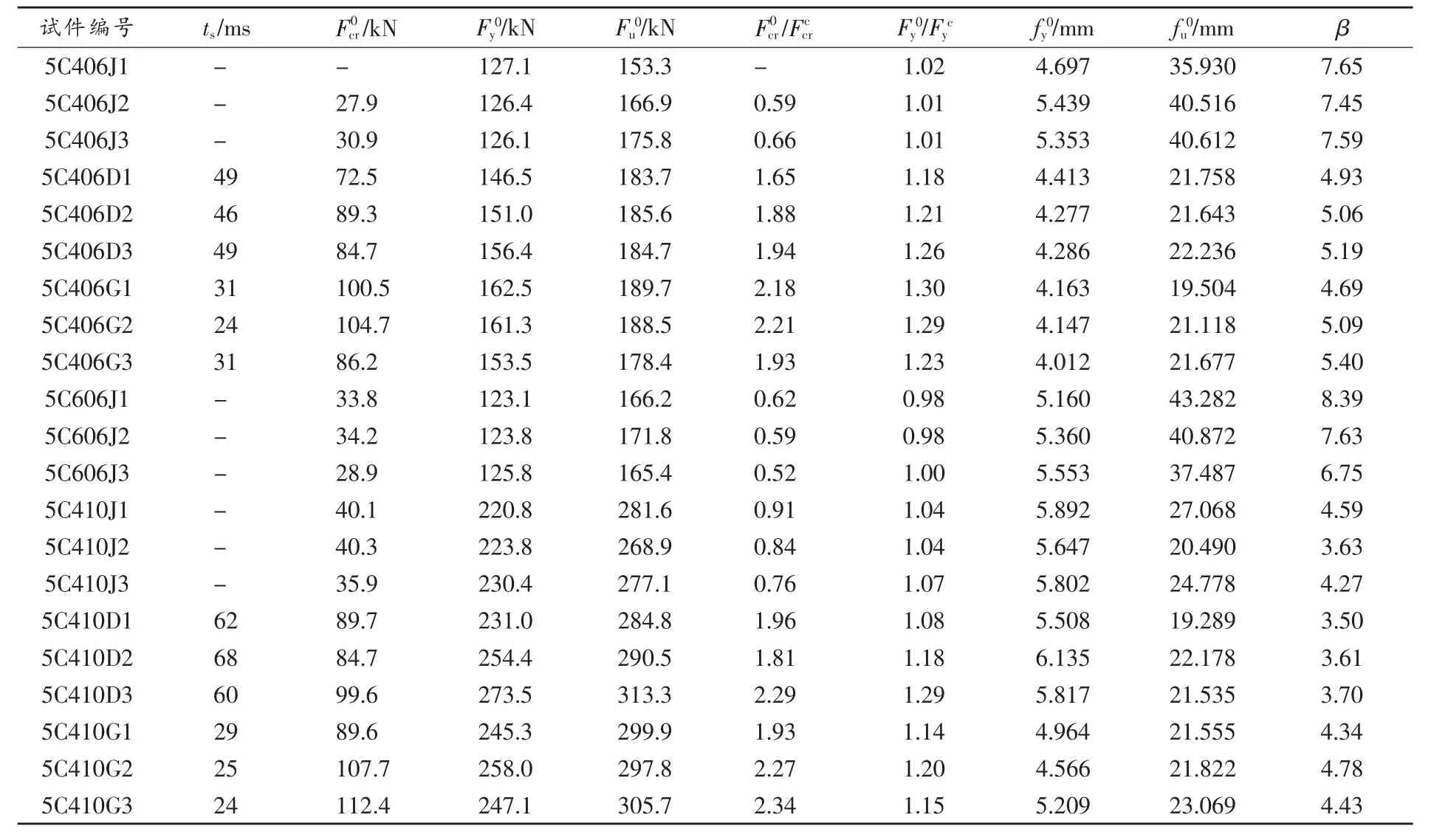
表4　试验结果汇总表

试验中的支撑钢梁在试验载荷范围内会产生一定的弹性弯曲变形，对试验梁的跨中挠度测量有一定影响，经试验测量和理论计算综合分析，支撑钢梁支座处的刚度约为350 kN/mm，即总载荷达到350 kN时支座处会产生1mm的沉降，在数据处理中已将该变形量对挠度测量的影响进行了修正。试件加载前放置在分配钢梁上，经计算由试件自重产生的最大弯矩约为0.22kN·m，仅占屈服弯矩的0.4%～0.8%，可将其影响忽略。

2.3对比分析

1）开裂载荷

本次试验中静载试验的开裂载荷实测值均小于其理论预估值，其原因可能是试件浇筑时振捣不够充分，另外试验时间为冬季，最低气温已降至0℃以下，试件内部混凝土可能已产生冻融损伤。

动载试验测得的开裂载荷较静载时有显著提升，提升幅度可达到100%～200%，提升的原因有两方面，一是混凝土抗拉强度在动态加载时比静态加载时可提升30%以上［6］，另一方面是由于静载试验和动载试验中确定开裂载荷的方法不同。静载试验中通过裂缝测宽仪放大40倍查找裂缝，发现裂缝的时间较为准确，在发现裂缝后至少保持载荷5 min，裂缝得以充分发展；而动载试验中是通过载荷-挠度曲线和载荷-钢筋应变曲线的拐点确定开裂载荷的，加载过程为瞬态连续加载，试件开裂后需经过一定时间的扩展才能使挠度和钢筋应变产生突增，而在这段时间内载荷还是不断增长的，曲线出现拐点的时间点比开裂时间点有一定的延迟，这也会导致从曲线中读取的开裂载荷比实际开裂载荷偏大。

2）屈服载荷

静载试验测得的屈服载荷与理论预估值十分接近，9个静载试件的试验结果中，Fy0/Fyc的平均值为1.017，说明静态加载时钢筋混凝土梁正截面受弯承载力的理论计算方法精度很高，同时也可验证静载试验的准确性。

动载试验时的屈服载荷较静载试验时有所提升，其比值见表5，表中数值为每组3个试件的平均值。由于适筋梁中钢筋屈服时受压区混凝土仍处于弹性阶段，钢筋混凝土梁的屈服载荷主要由钢筋的屈服强度决定，所以屈服载荷的提升幅度应与屈服强度的提升幅度密切相关。动载试验中低速加载时钢筋应变率为0.045～0.065s-1，受压表面混凝土应变率为0.023～0.026s-1，高速加载时钢筋应变率为0.09～0.125s-1，受压表面混凝土应变率为0.032～0.046s-1。根据文献［6］和文献［14］中的结果，低速加载时可取钢筋屈服强度提高系数为1.05，混凝土抗压强度提高系数为1.15，高速加载时可取钢筋屈服强度提高系数为1.10，混凝土抗压强度提高系数为1.17，将考虑动态强度提高系数后的材料参数代入静态屈服载荷的计算公式，可计算得到低速加载时屈服载荷提高系数为1.054～1.059，高速加载时屈服载荷提高系数为1.103～1.105，屈服载荷提高系数与钢筋屈服强度提高系数十分接近，可近似取为钢筋屈服强度提高系数。配筋率较低的5C406组试件，屈服载荷提高系数实测值比计算值更大，而配筋率较高的5C410组试件，屈服载荷提高系数实测值与计算值相当。

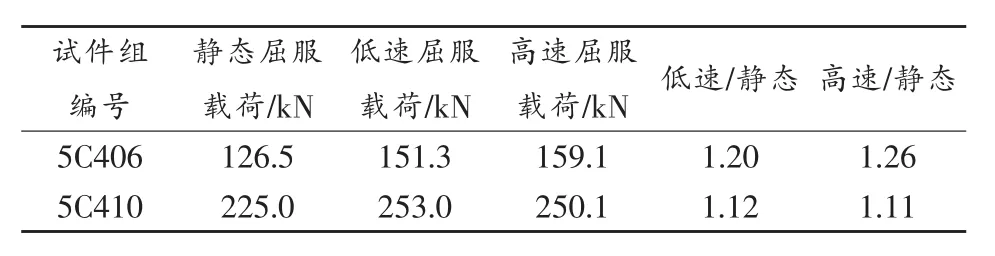
表5　梁试件屈服载荷对比

3）极限载荷与延性比

5C406组试件动载试验中并未测得试件真实的极限载荷，但动载作用下极限载荷肯定高于静载极限载荷。5C410组试件中部分动载试验后受压区混凝土破裂，可认为测得的极限载荷与真实的极限载荷十分接近，那么动载试验极限载荷平均值与静载试验平均值的比值为1.08，可作为极限载荷的提高系数，极限载荷的提高系数比屈服载荷的提高系数低一些。该组试件的延性比也可认为接近真实值，那么动载试验中试件延性比的平均值为4.06，与静载试验中延性比平均值4.16相近，而且动载试验中真实的延性比还会更高一些，说明动态加载时钢筋混凝土梁的塑性变形能力与静态加载时基本相当。

对比3种静载试验的结果，可发现混凝土强度对延性比影响较小，而配筋率对延性比影响显著，配筋率越高延性比越低。

3　结束语

通过HRB500钢筋混凝土简支梁的静动态抗弯试验，研究了不同混凝土强度等级（C40、C60）和不同配筋率（0.6%、1.0%）试件的受弯承载力，可以得到以下结论：

1）在动态载荷作用下，平截面假定依然成立，可以作为计算分析的基础。

2）动载试验中梁的开裂载荷有显著提升，提升幅度可达到100%～200%。

3）动载试验中梁的屈服载荷和极限载荷均有提升，可采用静载时计算屈服载荷的方法计算动态屈服载荷，但需要将钢筋和混凝土的静态强度替换为动态强度，而且这样计算对结构而言是偏于安全的。配筋率较低的梁动态屈服载荷的提高比例较高。

4）动态载荷作用下梁的延性比与静态加载时基本相当，配筋率越高延性比越低。

［1］混凝土结构设计规范：GB 50010—2010［S］.北京：中国建筑工业出版社，2011.

［2］林峰，顾祥林，匡昕昕，等.高应变率下建筑钢筋的本构模型［J］.建筑材料学报，2008，11（1）：14-20.

［3］李敏，李宏男.建筑钢筋动态试验及本构模型［J］.土木工程学报，2010，43（4）：70-75.

［4］MALVAR L J，ROSS C A.Review of strain rate effects for concrete［J］.ACI Materials Journal，1998，95（6）：735-739.

［5］MALVARLJ，ROSS C A.Review of strain rate effects for concrete in tension［J］.ACI Materials Journal，1999，96（5）：614-616.

［6］陈肈元.爆炸载荷下的混凝土结构性能与设计［M］.北京：中国建筑工业出版社，2015：103-109.

［7］钱七虎，王明洋.高等防护结构计算理论［M］.南京：江苏科学技术出版社，2009：37-45.

［8］方秦，柳锦春.地下防护结构［M］.北京：中国水利水电出版社，2010：179-188.

［9］都浩，邓芃，杜荣强.爆炸荷载作用下钢筋混凝土梁动力响应的数值分析［J］.山东科技大学学报（自然科学版），2010，29（6）：50-54.

［10］李振宝，宝小超.加载速率对钢筋混凝土梁动态性能的影响［J］.防灾减灾工程学报，2011，31（6）：627-631.

［11］肖诗云，许东.钢筋混凝土梁正截面率相关特性分析［J］.防灾减灾工程学报，2012，32（2）：152-157.

［12］李敏，李宏男.钢筋混凝土梁动态试验与数值模拟［J］.振动与冲击，2015，34（6）：110-115.

［13］混凝土结构试验方法标准：GB/T 50152—2012［S］.北京：中国建筑工业出版社，2012.

［14］李磊，何翔，王世合，等.新型高强钢筋快速拉伸试验研究［J］.防护工程，2015，37（5）：16-21.

（编辑：李妮）

Static and dynamic experimental investigation on flexural bearing capacity of HRB500 reinforced concrete beam

LI Lei1，2，HE Xiang1，2，SUN Ao1，WANG Shihe1，2，GAO Jie1
（1.Unit 61489 PLA，Luoyang 471023，China；2.He'nan Key Laboratory of Special Protective Materials，Luoyang 471023，China）

In order to study the flexural bearing capacity of HRB500 reinforced concrete simple supported beam，static and dynamic tests of three dividing point loading were carried out.21 beams in 7 groups were tested under 3 different loading speeds.The reinforcement ratio was 0.6% and 1.0%respectively，and the strength grade of concrete was C40 and C60 respectively.The strain distribution in the section，cracking load，yield load，ultimate load and ductility ratio were obtained.The comparative analysis of the experiment results show that，under dynamic load，plane section assumption is also tenable，and the cracking load of beam is significantly raised more than one time.The yield load and ultimate load increased a little.The dynamic yield load can be calculated by the method derived from static load condition，but the static strength of rebar and concrete must be replaced by the dynamic strength.The ductility ratio of beam is basically not influnced by loading speed，but it is lower when the reinforcement ratio is higher.

HRB500 rebar；concrete beam；dynamic experiment；yield load；ductility ratio

A

1674-5124（2016）10-0049-07

10.11857/j.issn.1674-5124.2016.10.010

2016-05-05；

2016-06-18

河南省科技创新人才计划（154200510028）

李磊（1980-），男，河南开封市人，助理研究员，博士，主要从事工程防护材料及其试验技术研究。