基于改进的QP算法和MPC理论的智能车纵向速度控制方法

周晶晶，徐友春，李明喜

(1.军事交通学院 研究生管理大队，天津 300161； 2.蚌埠汽车士官学校 运输勤务系，安徽 蚌埠 233011；3.军事交通学院 军用车辆系，天津 300161)



● 车辆工程Vehicle Engineering

基于改进的QP算法和MPC理论的智能车纵向速度控制方法

周晶晶1，2，徐友春3，李明喜3

(1.军事交通学院 研究生管理大队，天津 300161； 2.蚌埠汽车士官学校 运输勤务系，安徽 蚌埠 233011；3.军事交通学院 军用车辆系，天津 300161)

基于模型预测控制(MPC)理论的智能车纵向速度控制问题可以转换为二次规划问题。针对该二次规划(QP)问题，利用一种改进的有效集(IASM)二次规划算法减少MPC计算成本。该方法包含两步：首先对等式约束引进一种降维算法；然后利用梯度投影方向对有效集算法的搜索方向进行改进。改进的QP算法减少了迭代次数，降低了MPC纵向控制的计算成本。仿真结果证明了该方法的有效性。

二次规划；改进的有效集算法；模型预测控制；纵向速度控制；智能车

模型预测控制(model predictive control，MPC)是20世纪80年代初发展起来的一类新型控制算法。MPC直接运用于工业过程控制的实际应用，并在与工业应用的紧密结合中不断地完善和成熟[1]。文献[2-4]将MPC运用于智能车的横向或纵向控制，均取得了一定的效果。但目前面临的主要问题之一是在优化目标较多时计算成本较高，影响智能车控制系统实时性的要求。本文讨论MPC转化为二次规划(quadratic programming，QP)问题后，通过改进QP算法来降低计算成本，提高MPC的实时性。

QP问题的求解方法很多，可以采用内点法[5]、并行二次规划法[6]、有效集法(active set method，ASM)或者原始对偶法[7]等求解。其中等式约束凸二次规划一般采用零空间法[8-9]和拉格朗日法[7]；一般凸二次规划常用方法是有效集法和内点法。本文首先将基于MPC理论的智能车纵向速度控制问题转化为QP问题；而后针对该问题，利用一种改进的有效集二次规划算法减少迭代次数、改进搜索方向以减少计算量；最后用Matlab进行仿真验证。

1　MPC纵向速度控制问题转化为QP问题

车间运动学模型是一种简单描述两辆同向行驶的车辆之间位置变化关系的数学模型[3](如图1所示)。建立xoy坐标系，被控车辆位置为xh，其速度、加速度为vh、ah；目标车辆位置为xd，其速度、加速度为vd、ad；两车间相对距离、相对速度和相对加速度为xr、vr和ar；期望车间距和实际车间距分别为Δxdes、Δx，δ为二者间距误差。

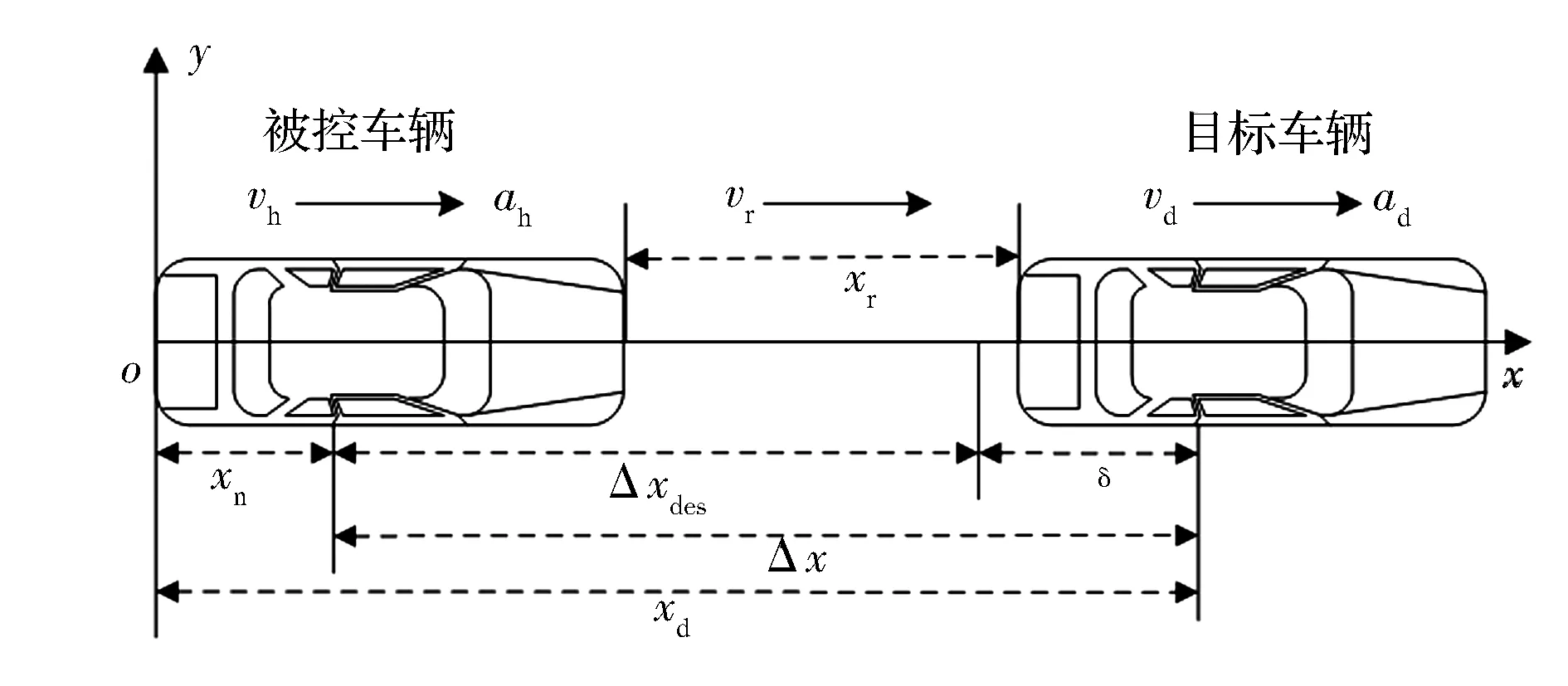
图1　车间运动学模型示意

在李明喜等[3]、罗莉华等[4]车间运动学模型的基础上，建立如下模型。其中两车间相对距离xr、相对车速vr可由安装在智能车前方的雷达测得，被控车辆的速度vh、加速度ah可由车载惯导测得。设采样时间为Ts，执行器惯性环节时间常数为τ，期望加速度指令(控制输入)为u，车辆的加加速度(加速度的导数)为j，反应Δxdes的时间常数为χ。为了保证安全，采用鲁棒MPC的思想，把前面车辆的加速度视为有界干扰，并对车间运动学模型进行离散化。在初始时刻(t=0)条件下，车间运动学方程为

(1)

将目标车辆加速度ad(k)视为控制系统的扰动w(k)，控制变量向量u(k)=[ah(k)]，状态变量向量x(k)=[Δx(k),vr(k)，vh(k)，ah(k),jh(k)]T表示相对距离、相对速度、本车速度、本车加速度、本车加加速度；y(k)=[δ(k),vh(k),ah(k),jh(k)]T为输出变量向量，表示车间距误差、本车速度、本车加速度、本车加加速度。车间纵向运动学模型为

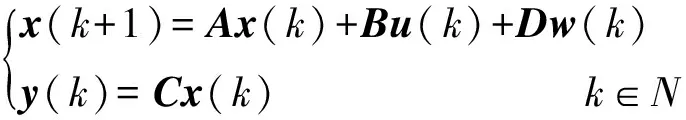
(2)

式中：x为5维状态向量；u为控制输入向量；w为系统扰动输入向量；y为输出向量；A、B、C、D分别为状态矩阵、控制输入矩阵、状态输出矩阵及扰动矩阵，各系数矩阵如下：

同时为保证纵向控制的平稳性和舒适性，在设定y(k)的参考轨迹时，取平稳趋近于y(k)期望值的指数衰减函数作为参考，其函数为

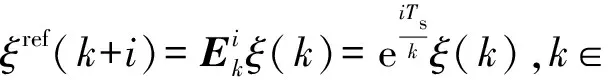
式中：τδ、τv、τa、τj分别为相应参考轨迹的时间常数；E=diag[Eδ，Ev，Ea，Ej]，且均在(0，1)区间，则参考轨迹向量为

yref=(k+i)=Eiy(k)，i=1,2,…Np

搭建好纵向控制的预测模型之后，智能车纵向控制的目标函数J可以构建为

(3)

式中：ε为松弛因子；ρ为松弛因子权重系数；Q为输出变量权重矩阵；R为控制变量权重矩阵；Np、Nc分别为MPC的预测时域和控制时域。

此外，为保证智能车纵向控制的安全性(d0为最小安全距离)、平稳性和舒适性，状态变量及输出变量需要满足如下约束条件：

因此，可将基于车间运动学和MPC理论的智能车纵向速度控制问题转化为式(4)带有等式、不等式约束的QP问题：

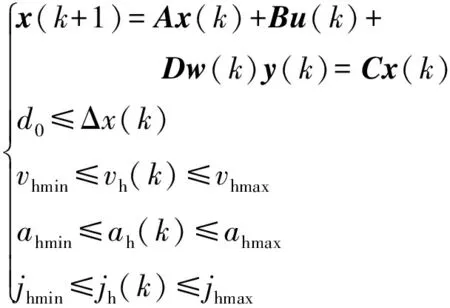
(4)

2　QP问题求解优化

考虑一般的QP问题表达式为

(5)

式中：H为n×n阶对称方阵(Hessian矩阵)；c为常数向量。

有效集法求解QP问题的基本原理为：从一个初始点x0开始计算，用拉格朗日乘子法求解等式约束子问题得到全局极小点和对应的拉格朗日乘子dk、λk。若dk=0且等式约束子QP问题是原QP问题的可行解，则判断λk的正负：若λk非负，则该解是全局极小点，停止迭代；若λk为负，则去掉一个约束重新求解等式约束子问题。若dk不为零，重新确定搜索方向和步长因子，调整有效集。若等式约束子QP问题不是原QP问题的可行解，那么需要增加约束继续迭代求解所得的QP问题。

2.1等式约束QP求解的改进

首先考虑式(6)的等式约束QP问题(ECQP)的改进方法。为解决此问题，采用文献[11]中的降维算法(dimension reduction algorithm，DRA)。

(6)

设H、A矩阵及x、b、c向量为

x=[x1x2…xn]T

b=[b1b2…bn]T

c=[c1c2…cn]T

设A行满秩，即r(A)=m，A中一个非奇异子矩阵为M，且A=M+N，M、N分别为

其中，{i1，…，im}∪{j1，…，jp}={1，2，…，n}，

m+p=n。J对x求梯度：

▽J(x)=Hx+c=P(x)+Q(x)

(7)

式中P(x)、Q(x)分别为

令N*=M-1N，增广矩阵(A，b)经初等行变换变为(A*，b*)，则式(6)的ECQP问题转换为

(8)

相应地满足Kuhn-Tucker条件的拉格朗日乘子为λ=-(M-1)T(Hmx+cm)。ECQP问题降维算法流程如图2所示。可以发现，DRA算法和拉格朗日乘子法求解ECQP问题都是通过求解方程组得到最优解，但DRA算法中方程组个数为n个，而拉格朗日乘子法方程组个数为m+n个，DRA算法维数降低，减少了存储空间和计算成本。

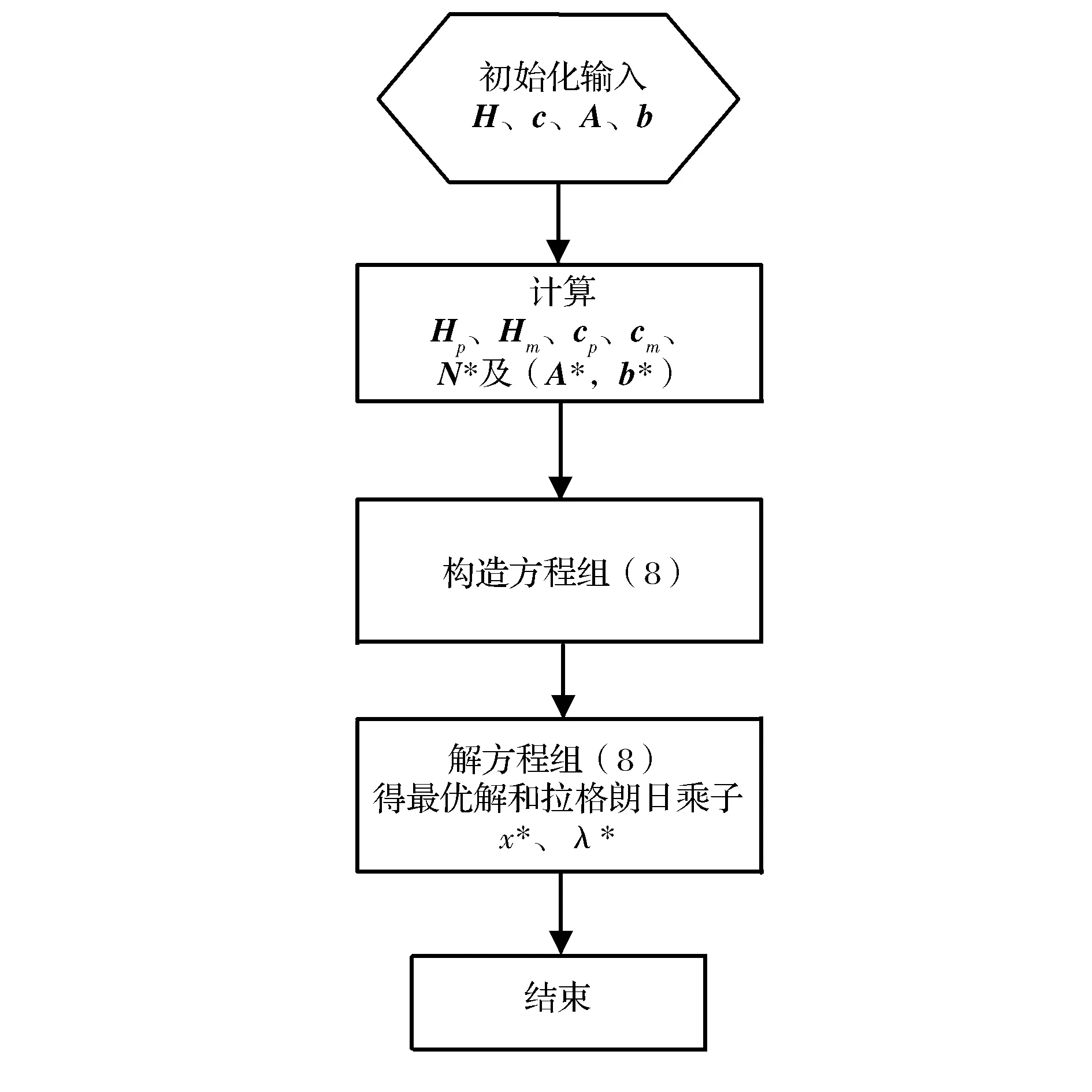
图2　ECQP问题DRA算法流程

2.2改进的QP问题求解算法

式(5)的一般QP问题中，定义如下集合：I(x)={i∈I|aiTx=b}，S(x)=E∪I(x)为有效集。文献[10]已经证明：若H矩阵是半正定的，则式(5)是一个凸二次规划；如果有至少一个向量满足约束并且在可行域有下界，则凸二次规划问题就有一个全局最小值；如果H是正定的，则式(5)为严格的凸二次规划，那么全局最小值是唯一的。从图2可以看出，当ECQP的最优解不是式(5)QP问题的可行解时，xk+1=xk+αkdk中虽然保证沿下降方向搜索，但不能确定是最速下降方向。为了提高QP算法的收敛速度，采用文献[12]中的梯度投影算法(gradient-projection algorithm，GPA)，用GPA算法解决最速搜索方向问题。为改进搜索方向，设xk是式(5)QP问题的可行解，有效集为S(xk)=E∪I(xk)。

(9)

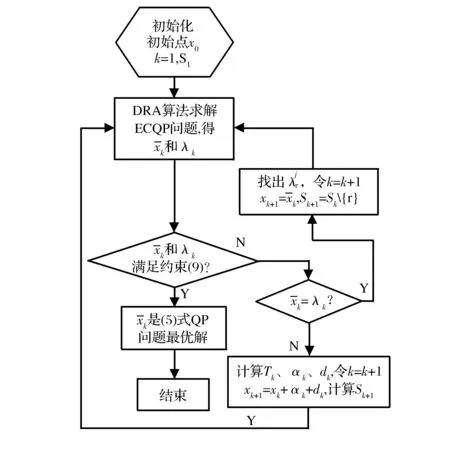
图3　IASM算法流程

3　IASM数值和Matlab仿真实验

3.1IASM算法数值实验

利用Matlab实现上述IASM算法，并与Matlab优化工具箱中的QUADPROG算法(以下简称QP算法)及文献[7]中的希尔德雷思二次规划(hildreth quadratic programming，HQP) 算法比较，将IASM算法与QP、HQP算法在迭代次数、计算时间(10次取平均值，单位ms)进行对比。IASM算法使用Matlab(R2010a)编写。采用文献[13]中的典型测算例进行对比测试，P为算例编号、n为优化变量数、x0为初始点，对比结果见表1，其中A1为HQP算法、A2为QP算法、A3为IASM算法。

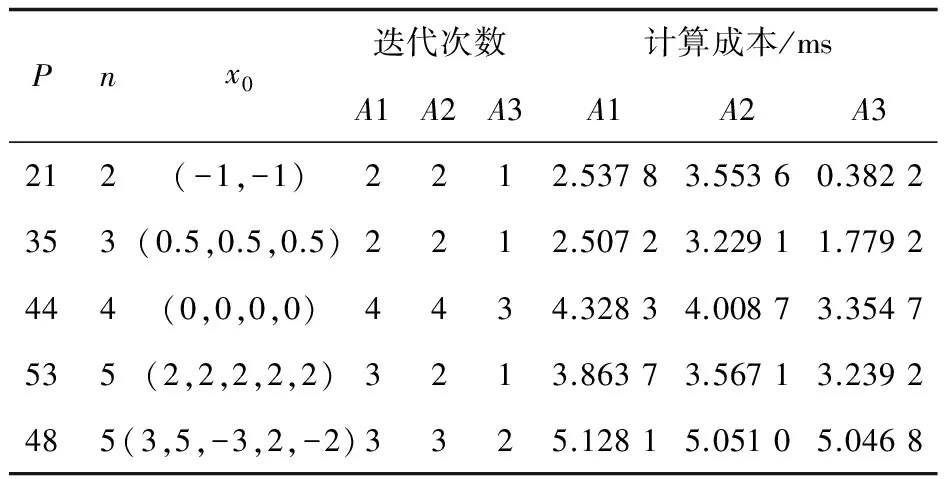
表1　IASM算法与QP、HQP算法算例对比

3.2纵向速度控制Matlab仿真

运用上述算法，解决式(4)的基于车间运动学的和MPC理论的智能车纵向速度控制问题。仿真参数值为：Np=15，Nc=5，Ts=0.01 s,Nsim=400，χ=1.2 s，τ=τδ=τv=τa=τj=0.5 s，d0=Δx=5 m，xh0=5 m/s。输出变量权重系数和控制变量权重系数分别为0.6和0.8；约束条件为vhmin=0 m/s，vhmax=5 m/s，ahmin=0m/ s2，ahmax= 4 m/s2，jhmax= 0 m/s3，ahmax= 0.8 m/s3，改变预测时域Np，3种算法的MPC计算成本(单位ms)对比见表2。

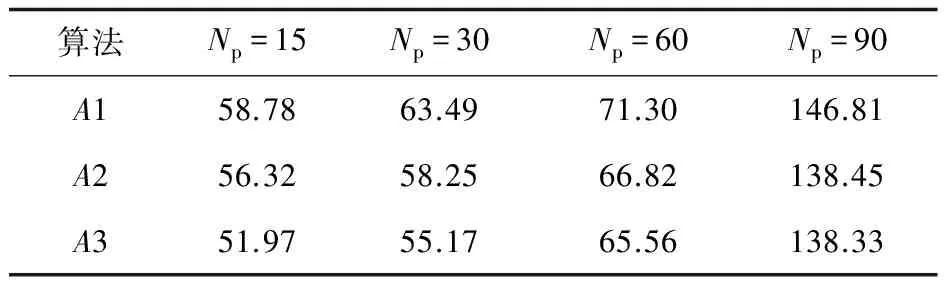
表2　MPC计算成本对比　ms

通过表1可以看出，在优化变量数n较少(n≤4)时，IASM算法迭代次数较少，计算成本比QP及HQP算法更低；当优化变量数n增加到一定程度(n≥5)时，IASM算法计算成本优势不明显，原因是在求解最速搜索方向时需要计算梯度投影。仿真结果表明算法是有效的。表2表明，在相同初始条件和预测时域下，IASM算法计算有一定优势。Np≤60时，计算成本小于智能车实时控制周期100 ms，满足控制实时性要求。

[1]李国勇.智能预测控制及其MATLAB实现[M].2版.北京:电子工业出版社,2010:255-268.

[2]FALCONE P, BORRELLI F, ASGARI J, et al. Predictive active steering control for autonomous vehicle systems[J]. Control Systems Technology, IEEE Transactions, 2007, 15(3): 566-580.

[3]李明喜,章永进,彭永胜,等.车间运动学模型在智能车速度跟踪控制中的应用[J].军事交通学院学报.2015,17(11):49-53.

[4]LUO Lihua, LIU Hong, LI Ping, et al. Model predictive control for adaptive cruise control with multi-objectives: comfort, fuel-economy, safety and ca-following[J]. Journal of Zhejiang University SCIENCE A, 2010,11(3):191-201.

[5]KUHNE F, LAGES W F. Model predictive control of a mobile robot using linearization[J]. Proceedings of Mechatronics and Robotics, 2004:525-530.

[6]BRAND M, SHILPIEKANDULA V, YAO C, et al. A parallel quadratic programming algorithm for model predictive control[C]//Proc. 18th World Congress of the International Federation of Automatic Control, 2011,18(1): 1031-1039.

[7]WANG Liuping. Model Predictive Control System Design and Implementation Using MATLAB[M]. London: Springer, 2009:60-73.

[8]卢桂馥,王勇,邹健.一种快速的零空间算法[J].西安交通大学学报,2012,46(2):59-63.

[9]桂湘云,刘树成.一般二次规划问题的交换型零空间方法[J].应用数学学报,1988,11(2):209-221.

[10]马昌凤.最优化方法及其Matlab程序设计[M].北京:科学出版社,2010:190-211.

[11]易颖华.二次规划的改进有效集算法[D].南昌:江西师范大学,2008:8-13.

[12]崔睿贇.求解凸二次规划的自适应投影梯度算法[D].南京:南京大学,2009:14-20.

[13]HOCK W, SCHITTKOWSKI K. Test Examples for Nonlinear Programming Codes[A]. Lecture Notes in Economics and Mathematical Systems.Berlin: Springer-Verlay, 1981, Vol. 187:44-76.

(编辑：张峰)

Longitudinal Speed Control Method of Intelligent Vehicle Based on Improved QP Algorithm and MPC Theory

ZHOU Jingjing1,2, XU Youchun3, LI Mingxi3

(1.Postgraduate Training Brigade， Military Transportation University， Tianjin 300161， China；2.Transportation Service Department， Bengbu Automobile NCO Academy， Bengbu 233011， China；3.Military Vehicle Department， Military Transportation University， Tianjin 300161， China)

The problem of longitudinal speed control of intelligent vehicle based on MPC (model predictive control) theory can be converted to QP (quadratic programming) problem. Considering this QP problem, the paper proposes a method which can reduce MPC costs with IASM(improved active set method). Firstly, it introduces a dimension reduction algorithm for equality constraints. Then, it improves the search direction of active set algorithm with gradient-projection direction. The improved QP algorithm reduces the number of iterations and the computational cost of MPC longitudinal control. The simulation result verified the effectiveness of the method.

QP; IASM； MPC longitudinal speed control; intelligent vehicle

2016-06-02；

2016-08-23．

国家自然科学基金项目(91120306;91220301).

周晶晶(1986—)，男，硕士研究生；

徐友春(1972—)，男，博士，教授，博士研究生导师．

10.16807/j.cnki.12-1372/e.2016.10.012

TP273

A

1674-2192(2016)10- 0049- 05