基于复杂网络理论的国防公路网鲁棒性研究

蒋益伟，范精明，尹福文，周　伟，宋　恒

(1.军事交通学院 研究生管理大队，天津 300161； 2.军事交通学院 训练部，天津 300161；3.南京陆军指挥学院，南京 210045； 4.天津警备区 司令部，天津 300050)



● 国防交通National Defense Traffic

基于复杂网络理论的国防公路网鲁棒性研究

蒋益伟1，范精明2，尹福文1，周伟3，宋恒4

(1.军事交通学院 研究生管理大队，天津 300161； 2.军事交通学院 训练部，天津 300161；3.南京陆军指挥学院，南京 210045； 4.天津警备区 司令部，天津 300050)

明确国防公路网鲁棒性的定义，选取某省国防公路网中桥梁、隧道作为节点，运用UCINET生成拓扑图；基于复杂网络理论，利用Matlab编程分别模拟某省国防公路网在随机、度优先和介数优先3种攻击策略下，网络效能的变化。结果表明：在介数优先攻击下，某省国防公路网表现出较差的鲁棒性；度优先攻击下鲁棒性较介数攻击略好；而在随机攻击下，表现出较强的鲁棒性。

复杂网络理论；国防公路网；网络效能；鲁棒性

从现代几场高技术战争来看，精确打击敌方重点交通目标，破坏其交通保障线，成为一种新型作战方式。美军在新颁布的《空中作战》中对“五环目标”理论进一步细化，将“输送系统”作为第三位打击目标，这值得我们深思。随着我国大力建设公路基础设施，国防公路网日益发达，形成了一个复杂网络系统。路网中关键节点则是敌方打击的重要目标，一旦失效将会造成严重后果。本文基于复杂网络理论，运用Matlab模拟国防公路网遭受打击后网络效能的变化，得出鲁棒性分析，最后给出提高国防公路网鲁棒性建议，对于提高国防公路网保障能力具有重要的现实意义。

1　概念内涵

1.1复杂网络理论

复杂网络理论研究起源于欧拉的“七桥问题”，是一种用来描述自然、社会和工程领域中互相关联现象的理论。复杂网络理论的相关研究已取得相当多的成果，但目前学界对其还没有一个统一的定义。钱学森提出了一个比较被认可的定义：复杂网络是具有自组织、自相似、小世界、吸引子、无标度中部分或者全部性质的网络[1]。

复杂网络理论研究的基础是图论。根据图论，一个具体的网络如交通网络、电力网络、作战网络等，可以抽象为图G(V，E)，其中V为网络中的点集，G为边集。用数学方法将图转换成邻接矩阵，便于利用计算机编程计算。

1.2国防公路网鲁棒性

鲁棒性是系统网络的基本属性，是指系统在内部结构发生扰动的情况下，抵御外部干扰，仍可维持它预期功能或提供预期服务的能力。鲁棒性是系统的健壮情况，它是系统在异常和危险情况下得以生存的关键[2]。

结合鲁棒性定义和国防公路网的军事属性，将国防公路网鲁棒性定义为:国防公路网在受到敌方打击、恐怖分子袭击和自然灾害等情况下，其网络结构仍能维持稳定，以保障部队机动和完成运输任务的能力。

2　基础数据选取

在现代几场高技术战争中，西方发达国家采用精确制导武器大肆破坏敌方的交通设施。据统计，科索沃战争中南联盟共有50余座桥梁被毁，基本上使交通陷入瘫痪，军事部署无法进行，取得了不战而屈人之兵的效果。桥梁、隧道在交通运输网中起着跨越河谷、山川等障碍区域的作用，具有易损毁、难修复的特点，是交通网络中的重要节点。这些节点若遭受敌方精确打击损毁，短时间内难以修复，将会导致公路网运输能力大幅度下降，引起交通混乱，迟滞部队投送任务的完成。可以说，桥梁、隧道是公路输送系统中的咽喉，敌要破坏我公路输送系统，必定重点打击桥梁和隧道。

某省山地、丘陵占全省面积的80%以上，境内桥梁、隧道颇多，其中大型桥梁和隧道，战时必将成为敌方攻击的重点目标，这些公路控制节点若被摧毁，很有可能造成交通瘫痪，导致部队难以机动，影响作战进程甚至作战结局。

本文拟选取某省境内大型桥梁和隧道共198个节点，然后对所有节点进行编号排序生成节点集V(1，2，…，n)，节点间的连接状态作为边集E(i，j，y),其中i,j∈V；y为节点i和节点j的距离，构造网络图G(V，E),根据节点集V和边集E，利用Matlab编程生成邻接矩阵M，作为后续研究的基础数据[3]。运用网络分析软件UCINET载入邻接矩阵M生成某省国防公路网拓扑图(如图1所示)。

3　某省国防公路网鲁棒性分析

目前，运用复杂网络理论研究交通网络较多，且研究交通网络的可靠性较多，研究其鲁棒性较少。路网可靠性倾向从出行者的角度研究交通网络，路网鲁棒性是研究关键节点失效条件下，网络整体结构和性能的变化，侧重从网络自身的角度研究交通网。

3.1假设条件

为更好地分析国防公路网的鲁棒性，在研究前做以下假设：

(1)公路网线路一般具有双向通行能力，本文不考虑公路网线路的方向性，即本文所构造的某省国防公路网为一个无向网络。

(2)不考虑节点失效的概率和过程，本文只讨论节点失效后给网络带来的后果。

(3)节点遭受攻击后，损毁严重，短时间内难以修复，即在研究期内不考虑节点失效程度和修复性。

(4)节点的负载流量在其最大负载流量之内，不考虑由于流量过载导致级联失效的发生。

在实际情况中，节点遭受攻击后是不一定完全损毁的，且网络中某一节点的失效可能会引起级联失效的产生，但本文研究的侧重点是分析节点完全失效后，对网络鲁棒性产生的影响，暂不讨论节点失效的概率、程度以及级联失效的发生，因此做出以上假设是可行的。

3.2测度指标

为分析网络在遭受攻击的情况下所表现出的鲁棒性，对攻击造成节点失效后网络性能建立测度指标，来衡量节点按既定策略依次删除后对网络性能的影响。此类测度指标主要有全网效能、聚集系数、最大连通子图。

全网效能E(G)为路网中任意两点间的效能eij的平均值，节点i、j间的效能eij用此两点间最短路径dij的倒数表示。

(1)

从军事斗争的特殊性来看，最大连通子图规模和聚集系数虽然能反映网络拓扑结构的变化，但不能反映部队行程时间的变化，而部队行动恰恰对时间要求非常高，因此两个指标不适合军事运输网络测度指标。全网效能是由网络中两点间最短距离的倒数计算得来，当行驶速度一定时，全网效能值越大，最短路径越短，行程时间越短，运输网络越可靠。因此选用全网效能指标来测度国防公路网在遭受攻击时的鲁棒性，在遭受攻击时，全网效能值减少越慢，则说明网络鲁棒性越强，反之越弱。

3.3攻击策略

信息化战争背景下，精确打击已成为打击对方重要目标的主要手段，由于桥梁、隧道对公路交通运输控制作用，战时极易遭受敌方精确导弹攻击。敌方会在火力允许的条件下，根据掌握的情报资源，按照一定攻击策略，以造成最大破坏为目标打击我公路网[4-5]。

(1)随机攻击。当敌方不掌握路网任何信息时，随机选择目标展开攻击，以及台风、地震、设施老化等自然因素造成节点的失效，属于随机攻击，可利用程序随机删除网络中的节点，模拟随机攻击。

(2)度优先攻击。度是复杂网络理论中描述网络结构特征简单且非常重要的统计量。节点i的度ki为与该节点相连的路段的条数。从直观上看，某一节点的度值越大，就说明通过该节点的路段数越多，即节点越重要。

当敌方不能获取公路网全部信息时，会从直观上选择度值大的节点进行破坏袭击。利用Matlab模拟度优先攻击的过程：

步骤1：首先计算公路网中度值最大的节点，然后删除此节点，再计算测度指标值。 若有多个节点的度值相同，则选择排序最靠前的节点进行删除。

步骤2：在第一步完成的基础上，重新计算剩余节点中度值最大的节点展开攻击，再计算测度指标值，照此循环下去直至节点删除完毕。

步骤3：将每次删除节点后计算所得测度指标值存储，最后按比例以图的形式展示出来。

(3)介数优先攻击。节点i的介数定义为: 经过节点i的最短路径数目占网络中最短路径总数的比值。其数学表示式为

(2)

式中：bi为节点i的介数；V为网络的点集；ωvv′(i)为经过节点i的最短路径数目；ωvv′为网络中最短路径总数。

某一节点的介数反映了该节点对网络中其他节点联络和牵制作用，体现了节点在网络中的重要程度。公路网中节点介数越大，说明经过该点的最短路径越多，在战时对行程时间严格要求的情况下，经过该点的可能性越大，即节点的重要程度越高。因此，介数能够较好地识别网络节点的重要度。

利用Matlab编程模拟介数优先攻击，步骤与度优先攻击类似，每次攻击完后，程序自动计算剩余节点中介数最大的点进行攻击，直至最后一个节点。

在复杂网络理论中，介数和度是识别节点重要度的两个重要概念，度值和介数越大，说明节点越重要，越有可能遭受敌方的精确打击。因此，分别用介数优先攻击和度值优先攻击是模拟分析精确打击的一种有效手段，利用Matlab编程模拟某省国防公路网在随机攻击、度优先攻击和介数优先攻击情况下，根据网络效能的变化分析某省国防公路网的鲁棒性。

3.4结果分析

利用Matlab编程分别模拟随机、度优先和介数优先3种攻击策略下，某省国防公路网鲁棒性测度指标全网效能值的变化，结果如图2所示。

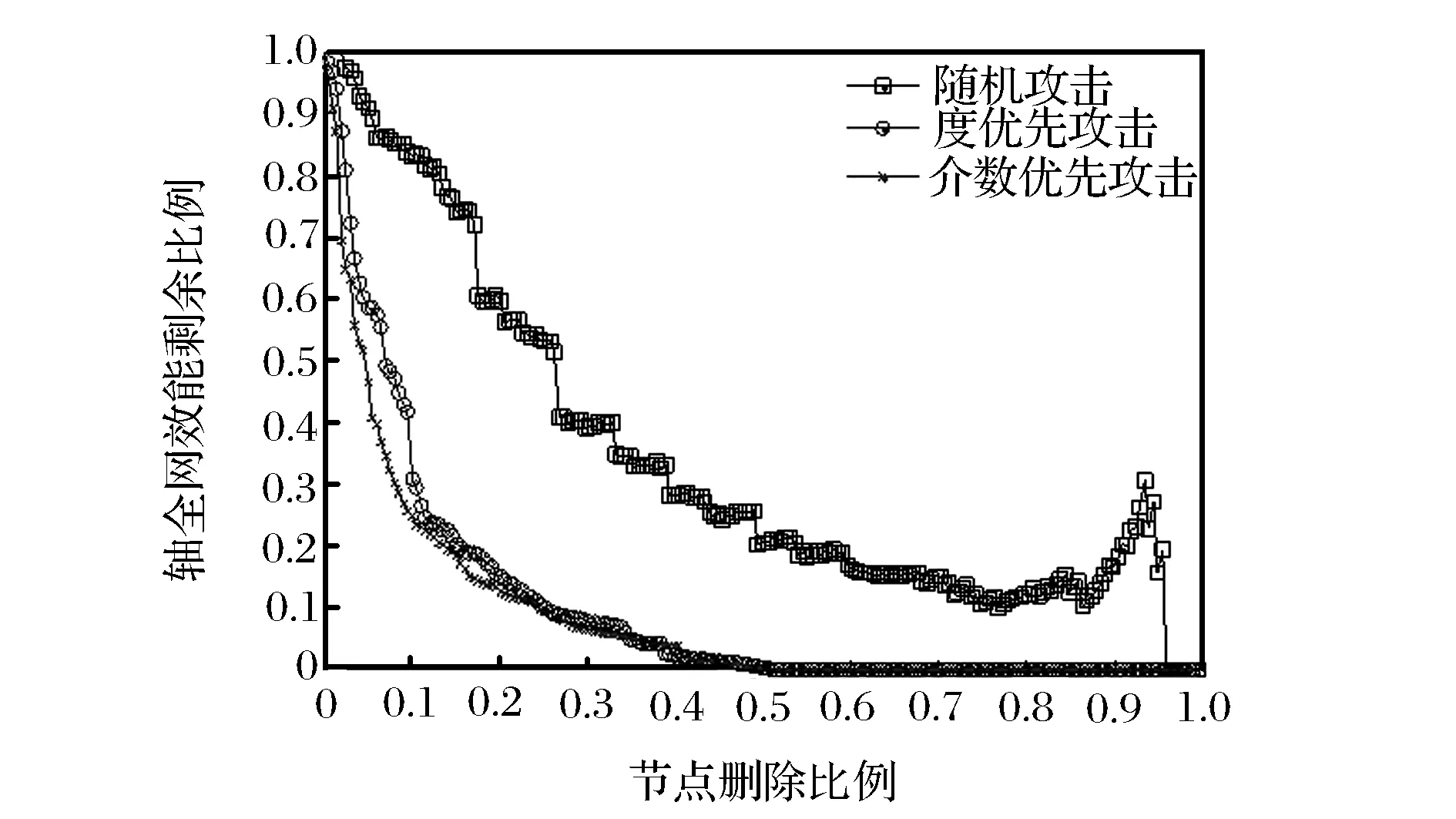
图2　3种攻击策略下全网效能值变化趋势

根据Matlab模拟攻击结果，作出以下分析：

(1)3种攻击策略中：介数优先攻击下，网络效能值下降得最快，某省国防公路网表现出较差的鲁棒性；度优先攻击效果次之；而在随机攻击下，公路网表现出较强的鲁棒性。介数优先攻击成为最优打击策略，这与介数定义是相符的，介数是根据最短路径计算得来，最能准确识别出国防公路网中节点的重要程度。

(2)介数优先攻击和度优先攻击具有良好的打击效果，而介数优先攻击更优。当仅删除网络中6%的节点时，介数攻击策略下，全网效能损失了59%；度优先攻击策略下，全网效能损失42%，这样的打击效果是惊人的，当删除网络中10%的节点时，可使网络丧失大部分运输能力，基本上使公路网陷入瘫痪。

(3)随机攻击模式下，全网效能降低相对缓慢，某省国防公路网表现出较好的鲁棒性。随机攻击下，全网效能值有几个明显呈跳跃降低的点，这是由于删除了网络中的重要节点导致的。在随机攻击的最后阶段，全网效能值明显增大，从全效能值的定义来看，这是因为当攻击到最后阶段时，删除节点对网络最短路径影响不大，而总节点数在减少，因此会造成效能值增大，而在介数优先和度优先攻击中，最短路径变化显著，故不会出现这种情况。这种情况只会在随机攻击的最后阶段才会出现，此时网络已经陷入瘫痪，因此这种情况的出现并不会影响测度指标全网效能的准确性。

4　结　语

国防公路网鲁棒与否，对于战时保障部队机动和运输至关重要。某省战略地位极其重要，根据上文的分析，可给出提高某省国防公路网鲁棒性的3点建议：

(1)公路建设前，进行充分论证、科学布局，优化干、支线的搭配，改善路网的拓扑结构，服务经济发展的同时，兼顾国防要求。

(2)参考节点介数，合理确定交通防护重点目标。从模拟攻击结果来看，介数攻击具有最优效果，而路网中介数较大的节点，不一定具有较大的度值，不容易引起注意，且当前制订交通防护方案时，不注重从网络角度进行考虑，因此可以借鉴复杂网络理论，科学确定交通防护重点目标。

(3)对路网中介数较大的节点，根据需要做好战备预案，战时采取浮桥、伪装等替代和防护措施，必要时建设迂回线、环线等备用线路。

[1]汪小帆，李翔，陈关荣.复杂网络理论及其应用[M].北京:清华大学出版社，2006：3-16.

[2]武云鹏. 鲁棒性军事行动过程方案生成与优化方法研究[D]. 长沙：国防科学技术大学，2012.

[3]马力，张明智.基于复杂网络的战争复杂体系建模研究进展[J].系统仿真学报，2015,27(2)：217-225.

[4]乔金锁，王喜富.煤炭运输网络结构鲁棒性评价及应用研究[J].交通运输系统工程与信息，2013,13(4):126-132.

[5]胡鹏，帅斌，狄兆华.突发状况下危险品运输网络鲁棒性建模和仿真[J].交通运输系统工程与信息，2015,15(2): 109-115.

(编辑：闫晓枫)

Robustness of National Defense Highway Network Based on Complex Network Theory

JIANG Yiwei1, FAN Jingming2, YIN Fuwen1, ZHOU Wei3, SONG Heng4

(1.Postgraduate Training Brigade, Military Transportation University, Tianjin 300161, China;2.Training Department, Military Transportation University, Tianjin 300161, China;3.Nanjing Army Command College, Nanjing 210045, China； 4.Command of Tianjin Garrison， Tianjin 300050, China)

Firstly, the paper introduces the definition of robustness of national defense highway network, and generates topological graph by UCINET with bridge and tunnel of a province’s national defense highway network as node. Then, with mat lab, it simulates the changes of network efficiency under random, degree first and betweenness first attack respectively based on complex network theory. The result shows that the national defense highway network appears to bad robustness under betweenness first attack and better under degree first attack, and best robustness under random attack.

complex network theory; national defense highway network; network efficiency; robustness

2016-04-07；

2016-04-19．

蒋益伟(1991—)，男，硕士研究生；

范精明(1963—)，男，博士，教授，硕士研究生导师．

10.16807/j.cnki.12-1372/e.2016.10.006

U412．1

A

1674-2192(2016)10- 0024- 04