基于改进遗传粒子滤波与SME的多目标跟踪算法*

熊志刚，黄树彩，吴潇，苑智玮

（空军工程大学防空反导学院，西安710051）

基于改进遗传粒子滤波与SME的多目标跟踪算法*

熊志刚，黄树彩，吴潇，苑智玮

（空军工程大学防空反导学院，西安710051）

针对基于对称量测方程的多目标跟踪，传统的滤波手段无法解决因对称变换带来的非高斯问题，提出一种新的遗传粒子滤波方法。新的滤波算法利用粒子的噪声含量与权值的负相关，改进了更新过程中权值计算所依赖的概率密度函数，避免了新量测噪声的求解。同时利用遗传算法的优势，保障了粒子的多样性，提高了粒子的使用效率，防止了滤波发散及局部最优。仿真结果表明，基于对称量测方程的多目标跟踪中，改进的遗传粒子滤波算法较扩展卡尔曼滤波算法、不敏卡尔曼滤波算法和联合概率数据关联滤波算法跟踪效果更好。

多目标跟踪，对称量测方程，遗传粒子滤波，非高斯，权值计算

0　引言

数据关联是多目标跟踪的关键和难点。联合概率数据关联（Joint Probability Data Association，JPDA）［1］在目标数目已知的条件下，可以通过数据关联的手段，对多个目标的状态进行估计，完成多个目标的跟踪。但是，随着目标数目的增加，JPDA计算十分复杂。对称量测方程（Symmetric Measurement Equation，SME）是Kamen针对多目标跟踪中的数据关联而提出的一种新方法［2］。SME在传统的多目标跟踪模型的基础上引入了一组对称变换方程，通过这组方程对观测量进行对称变换，产生新的量测来实现多个目标状态的更新，有效避免了数据关联。SME虽然成功解决了数据关联的问题，但也带来了新的挑战。对称变换不仅有加法运算，还包括元素的相乘，这就会带来非线性问题。另外，虽然原来的量测噪声是服从高斯分布的，但是经过乘法运算之后，新的量测噪声不一定服从高斯分布，也就是会产生非高斯问题。对于非线性问题，一些经典的非线性滤波算法，如扩展卡尔曼滤波算法（ExtendedK almanFilter，EKF）［3］和不敏卡尔曼滤波算法（UnscentedKalmanFilter，UKF）［4］可以很好地解决。至于非高斯问题，有学者引入了高斯组合近似的方法［5］，然而，随着目标数目的增加，近似方法计算异常复杂。

本文就SME非高斯问题作了相关研究，并提出了一种依靠改进的遗传粒子滤波（Genetic Particle Filter，GPF）的解决办法，核心思想是：基于权值和粒子的噪声含量的负相关，建立反比例模型，在更新阶段对权值进行计算。同时，为保障粒子的使用效率，本文根据所研究的内容，引入并改善了遗传算法。

1　多目标跟踪模型

基于改进GPF-SME多目标的跟踪中，跟踪模型由3部分组成：联合的目标运动模型、联合的目标观测模型、对称量测方程。

1.1联合的目标运动模型

则k时刻的联合目标机动模型可以表示为：

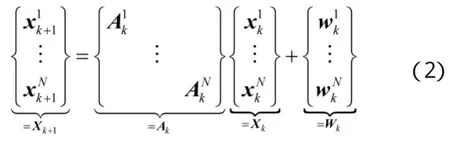
1.2联合的目标观测模型

假设k时刻N个目标的观测值是可以得到的，没有虚警，也没有漏警。目标观测模型是：

则k时刻，对目标的联合观测：

1.3对称量测方程

SME的核心思想是，利用原始的观测数据，通过对称变换，构造新的量测值，并利用新的量测值来实现目标状态的最优估计。常用的对称变换方式有乘积和、幂次和。

本文中，考虑二维平面上两个目标的跟踪，原始的观测数据为目标的位置。引入复平面坐标系，则目标在复平面中的位置可表示为，然后结合平方和的对称变换形式可以得到对称量测方程：

由式（5）可知，经过对称变换得到的新量测值并不受原始观测数据排列的影响。这样，就避免了数据关联。

2　遗传粒子滤波

GPF主要是将遗传算法中的选择、交叉、变异等进化思想引入到粒子滤波算法中，代替传统的重采样的方法［6］。

GPF将权值作为粒子的适应度，适应度的方差对应粒子重要性权值的方差。理论上，当适应度方差满足要求时，所有的粒子都是合理粒子，应当保留。反之，则需要进行选择、交叉、变异。

2.1初始化

基于先验概率分布p（x0）和初始化的状态x0采样得到粒子集，并令粒子所有的权值为1/N。

2.2权值更新

k时刻，粒子权值更新的公式如下：

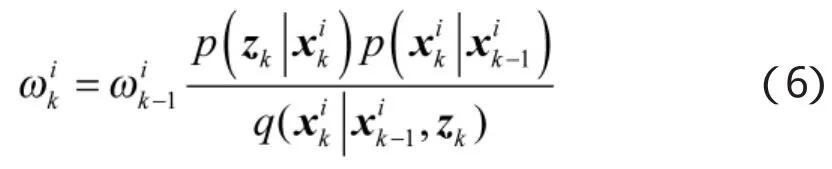
对权值进行归一化处理：

2.3遗传

计算粒子的权值方差。若方差Sω符合要求（小于设定的阈值Noff），则保留粒子为，并直接转到第4步；如果权值的方差不符合要求，则需要对粒子进行交叉、变异。

2.4估计并输出状态值

2.5状态预测

3　改进的GPF-SM E算法

3.1基于负相关的权值计算

GPF算法和SME滤波手段的结合涉及到更新阶段权值计算所依赖的概率密度函数的求解，yk为新的量测值。基于似然函数服从高斯分布（简称py）计算公式如下：

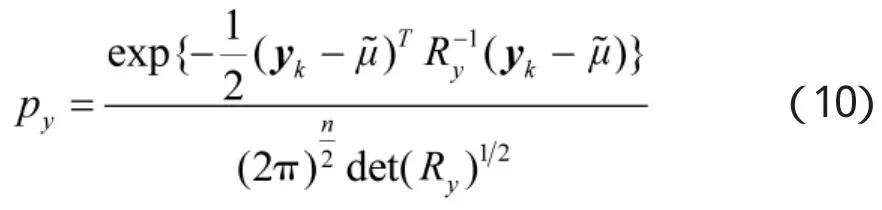
由式（10）可知，似然函数的计算需要得到新的量测噪声Ry，Ry计算很复杂［4］。而且，从式（5）中可以看出，对称变换既有乘法运算又有加法运算，得到的新量测变量不一定服从高斯分布。因此，需要对更新阶段权值计算方式作改进。

王秋平在文献［7］中对粒子滤波权值计算作了改进，中心思想是：基于反比例函数和高斯函数在第1象限的相似性，用反比例函数取代高斯函数作为更新过程中权值计算依赖的概率密度函数，以实现粒子的权值更新。从图1中可以看出反比例模型更能够区分噪声粒子的差别，降低误差。由此可以得到新的粒子权值计算方法：

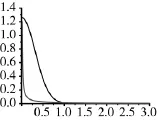
图1　反比例模型和高斯模型

3.2选择

由于粒子的权值比较小，受计算机能力的限制，计算粒子权值的方差Sω和阈值Noff比较作为选择的依据在仿真操作中是难以实现的。本文采用权值平方和作为选择判断的标准［8］：

根据式（12），当Ne≥N/3时保留所有粒子，否则进行交叉和变异操作。

3.3交叉

本文编码方式是浮点数编码，选择算术交叉算子，具体实施步骤是，随机选取粒子，按照以下方式进行交叉操作：

3.4变异

变异的两个重要因素是变异概率Pm和变异算子。变异算子对粒子的多样性十分重要。

变异算子：对粒子集的权值按从大到小的方式为标准正态分布，η本进行排列：。选择前Ns=Ps×N个粒子，按照下列方式进行变异操作：

3.5新的滤波算法流程

3.5.1初始化

3.5.2权值更新

对采样粒子集和原始观测值，由观测式（4）和对称量测式（5）可得到新的量测值，然后根据式（8）和式（11）对粒子的权值进行更新。

3.5.3遗传

按改进的遗传算法对粒子进行选择、交叉、遗传和变异得到粒子集。

3.5.4状态估计输出

基于以上得到的粒子集，根据式（1）可以对目标的状态进行估计。

3.5.5下一时刻的状态预测

需要说明的是，在遗传粒子滤波算法中，控制因子的设置十分关键。这些因子包括粒子数、交配概率Pc、变异概率Pm。关于遗传粒子滤波中关键控制因子的设置，本文参照文献［9］以及多次试验的结果选择如下：

表1　遗传粒子滤波控制因子

4　仿真

仿真场景设置：为便于观察，目标的数目设置为2，初始位置和速度分别为（0，1，0，1），（0，1，50，-1）；目标的运动分为4个阶段，前16个仿真步长内两个目标在平面内的两个方向均做匀速运动，16至26个仿真步长内目标在水平方向做匀速运动，26个仿真步长后恢复至原来的运动；目标的观测量为位置坐标，采样周期为1，σx=σy=1，仿真次数为80次。

图2表示目标真实的运动轨迹和观测值，图3为改进的GPF-SME对目标的跟踪效果展示，图4和图5为不同算法（UKF-SME、EKF-SME、JPDAF和改进的GPF-SME的RMSE比较。从图2和图3中可以看出，改进的GPF-SME对多目标跟踪的效果好，精度高。从图4和图5可以发现改进的GPF-SME滤波方法性能好于其他的算法。

5　结论

本文论述了基于改进的遗传粒子滤波与对称量测方程的多目标跟踪方法。基于对称量测方程的多目标跟踪中，非高斯问题突出，本文对此作了相关研究，并提出了GPF-SME滤波方法。GPF-SME滤波方法计算简便，在避免数据关联的基础上解决了非高斯问题。仿真结果表示，新算法能够有效实现多目标的跟踪。

［1］BAR-SHALOM Y，DAUM F，HUANG J.The probabilistic data association filter［J］.IEEE Contr.Systems，2010，29（6）：82-100.

［2］KAMEN E W.Multiple target tracking based on symmetric measurement equations［J］.IEEE Trans.AutomatContr.，1992，37（3）：371-374.

［3］LEVEN W F，LANTERMAN A D.Multiple target tracking with symmetric measurement equations revisited unscented Kalman filters，particle filters，and Taylor series expansions［J］.Proc.ofSPIE，2005，5810：56-67.

［4］LEVEN W F，LANTERMAN A D.Unscented kalman filters for multiple target tracking with symmetric measurement equations［J］.IEEE Trans.Automat Contr.，2009，54（2）：370-375.

［5］BAUM M，NOACK B，BEUTLER F，et al.Optimal Gaussian filtering for polynomial systems applied to association-freemulti-target tracking［C］//inInt.Conf.Inform.Fusion（FUSION），Chicago，Illinois，USA，2011：1-8.

［6］占荣辉，张军.非线性滤波理论与目标跟踪应用［M］.北京：国防工业出版社，2013.

［7］王秋平，周原，康顺.改进权值计算的EPF算法及在目标跟踪中的应用［J］.电光与控制，2011，18（4）：10-12.

［8］陈善静，杨华，曾凯.基于遗传算法的粒子滤波跟踪算法［J］.光电工程，2010，37（10）：16-22.

［9］张军，詹志辉.计算智能［M］.北京：清华大学出版社，2009.

Multi-target Tracking Algorithm Based on Advanced Genetic Particle Filter and Symmetric Measurement Equation

XIONG Zhi-gang，HUANG Shu-cai，WU Xiao，YUANZhi-wei
（School of Air and Missile Defense，Air Force Engineering University，Xi’an 710051，China）

To investigate the non-Gaussian problem caused by symmetry transformation while tracking multiple targets with symmetric measurement equation，which could not be solved by traditional filtering methods，an improved genetic particle filter is proposed.The advanced method uses the negative correlation between the noise component and the weight of particles to improve the probability density function upon which the weight calculation is dependent in the stage of update，and avoids the calculation of the new measurement noise.Meanwhile，genetic algorithm can help increase the use efficiency and diversity of particles as well as avoid the filter divergence and local optimization. Simulation was made，and it turned out that the filtering performance of advanced Genetic Particle Filter is better than Extended Kalman Filter，Unscented Kalman Filter and Joint Probability Data Association filter in multi-target tracking based on symmetric measurement equation.

multi-targettracking，symmetricmeasurementequation，geneticparticlefilter，non-Gaussian，weightcalculation

TN953

A

1002-0640（2016）10-0134-04

2015-08-18

2015-09-26

陕西省自然科学基金资助项目（2012JM8020）

熊志刚（1992-），男，湖北英山人，硕士研究生。研究方向：空天协同目标跟踪。