鱼雷装备备件隶属关系的两级库存系统配置优化研究*
2016-11-16魏勇穆连运
魏勇,穆连运
(海军潜艇学院,山东青岛266042)
鱼雷装备备件隶属关系的两级库存系统配置优化研究*
魏勇,穆连运
(海军潜艇学院,山东青岛266042)
备件库存系统配置优化是提高武器装备的战备完好性和降低寿命周期费用的重要途径,但在装备组成结构中,由于部件之间存在一定的隶属关系,并不是所有的项目都能够进行串件。针对现有两级库存系统备件配置优化研究的不完善之处,根据装备结构层次特点,通过分析鱼雷装备LRU和SRU备件两级库存系统,提出了备件初始配置方案下的备件库存缺货数模型,并在此基础上建立了基于备件隶属关系的两级库存系统配置优化模型。该模型以鱼雷装备使用度和库存费用为优化目标,通过优化备件库存配置结构,生成较好的备件库存配置方案,从而节约备件配置费用,避免造成资源浪费。
两级库存系统,优化配置,备件,隶属关系
0 引言
近年来,国内外对基于备件隶属关系的备件库存系统配置优化还未见到相关研究,仅有的研究主要局限于库存供应关系、可修件及不可修件等的情况。文献[1-2]建立了两级库存供应关系的装备常用备件初始配置模型和可修复航材存储策略模型,文献[3-4]建立了多级不可修件模型。这些模型均不能实现系统备件资源优化且不能解决一个仓储中心及多个分仓库的备件隶属关系的备件配置优化问题。本文研究对象是一个仓储中心及其多个同级分仓库的两级库存系统,分别针对仓储中心和基层级仓库的LRU和SRU备件的配置问题进行研究,使其在达到装备最优使用可用度要求的前提,尽量降低LRU和SRU备件配置费用。
1 问题描述与基本假设
1.1问题描述
由于SRU是LRU的分组件,两者之间存在隶属关系,所以SRU在库存系统中的运行与LRU的运行密不可分。因此,建立可修复、可更换件LRU和部分可修复、可更换件SRU在两级库存系统中的LRU+SRU的运行模式。其中:“+”表示隶属关系,“a+b”表示b隶属于a。LRU+SRU在两级库存系统中的运行模式如图1所示。

图1 LRU+SRU在两级库存系统中的运行模式
1.2基本假设
为简化问题,结合装备保障实际,进行以下关键性假设:
(1)一个仓储中心负责向k个基层级仓库供应备件,且每个基层级仓库都对应一个基层级维修单元;
(2)k个基层级维修单元和仓库负责完全相同型号的装备备件的维修和供应;
(3)某装备共有n种LRU,每种LRU又有m种分组件SRU;
(4)各基层级面对的LRU和SRU需求均服从泊松分布;
(5)不同类别的LRU和SRU需求相互独立,且需求量稳定;
(6)先到先维修,故障维修时间服从负指数分布,且每一个故障件的修理时间相互独立;
(7)仓储中心和各基层级库存均采取(S-1,S)和立即送修的策略;
(8)各分仓库之间不存在横向的备件转运和维修;
(9)LRU与SRU的重要程度不同,LRU缺货将导致飞机停飞,SRU缺货只延误LRU的修理时间;
(10)每一个SRU从属于唯一的LRU,且一件分组件SRU出现问题就可以使组件LRU发生故障;
(11)基层只负责LRU的修理,不对SRU进行维修,对故障的SRU只进行拆装替换。
2 LRU+SRU在两级库存系统中的配置优化模型
2.1仓储中心库存缺货数计算
从备件的运转流程可以看出,在一段时间内,部分备件送修,造成现有库存数低于初始备件库存量S,还有一些时间现有库存为0,在备件出现短缺时,在修备件大于S。因此,库存量可以表示为:

式中,SOH为现有库存数;SR为待接受备件数;SBO为短缺数,3个变量均是非负的随机变量。
当发生一次需求时,SR增加一件,若现有库存数大于0,它就减少一件,否则短缺数就增加一件,当修理完成后,SR减少一件,短缺数减少一件,或者是无短缺时SOH增加一件。因此,短缺数可以表示定义为:

2.1.1仓储中心SR U库存缺货数

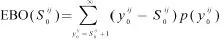
2.1.2仓储中心LR U库存缺货数


2.2基层级仓库库存缺货数计算
2.2.1基层级SR U库存缺货数
根据2.1节分析,当第i类LRU第j个分组件SRU在基层级仓库的库存量为时,可以得到基层级SRU库存期望缺货数为:
2.2.2基层级LR U库存缺货数
同理可以得到基层级LRU库存期望缺货数为:

2.3LRU+SRU的库存配置优化模型
2.3.1系统的装备使用可用度

则整个系统的装备使用可用度可表示为:式中,Nu表示第u个基层级负责保障的装备数量;Zi表示第i类LRU的单机安装数;γu为各基层级u的权重

2.3.2系统的备件库存费用
任务期[0,T]内系统的备件库存费用包括:系统的备件购置费用、储备费用、补货差旅费,以及缺货损失费[7]。
系统的备件购置费用:

由于库存补给策略为(S-1,S),则备件的总存储费用可近似为:

库存补给策略为(S-1,S),假设备件的寿命服从指数分布,则任务期[0,T]内总补货差旅费为:

系统的备件缺货费用为:

库存费用:

2.3.3备件配置优化模型[8-9]
模型I:以装备使用可用度为目标函数,保障费
用为约束条件:

模型II:以保障费用为目标函数,使用可用度为约束条件:

模型III:综合考虑可用度要求和库存费用约束:

3 算例分析
以一个仓储中心和两个基层级仓库组成的备件库存系统为例,对系统中各库存单元的备件配置进行优化。假设各基层级分别负责5条同型号鱼雷装备的备件保障,装备上的两种主要LRUi(i=1,2)组件和其所属的分组件SRUj(j=1,2)在系统中的单机安装数均为1,利用本文模型计算备件LRUi和SRUj的最优备件配置方案。表1给出了几种备件的相关参数信息。

表1 各仓库装备部件相关参考信息
根据建立的基于鱼雷系统使用可用度的库存优化模型,采用遗传算法进行求解[13]。定义个体适应度评价函数为:

遗传算法参数设计为:采用十进制编码,群体大小M=40,赌轮盘选择,交叉率为0.4,变异率为0.2。算法求解过程如图2所示。最终得到系统使用可用度为0.9386时的最优库存量如表2所示。
表2给出了经过优化后的6种备件的配置方案,各分仓库各备件的备件满足率如表2所示均达到要求。如果将备件全部置于分仓库达到相应的备件满足率要求需要6种备件的数量分别为:7,9,5,7,6,5。
通过优化配置结构可以节约的6种备件的数量分别为:2,2,1,1,2,1。从而可以节约费用630万元。随着分仓库的数目增加,中心仓库通过备件共享降低不确定性以减少备件配置费用的优势将更加明显,备件利用率将进一步提高。

图2 LRU+SRU最优库存求解过程性能跟踪

表2 各项备件的库存配置信息
4 结论
本文建立的模型可以对复杂装备的具有LRU+SRU隶属关系备件的两级库存系统进行优化,实现在备件费用和系统使用可用度约束条件下库存系统效能的最大化,并得出最优库存方案。利用该模型可以合理地调整各分仓库以及中心仓库各备件的配置数量,在达到备件满足率的基础上,减少备件配置费用,避免造成资源的浪费。通过算例分析,将全部备件配置与分仓库相比,该模型生成的备件配置方案需要更少的备件配置费用。需要说明的是该模型是稳态模型,且适用于寿命服从指数分布的备件。由于备件的需求量、维修时间和申请补给时间都是随机变量,存在不确定性,因此,备件保障系统实际上是一个复杂的离散事件系统,运用系统仿真优化的方法能提高计算精度,值得深入研究。
[1]周伟,郭波,张涛.两级供应关系装备常用备件初始配置模型[J].系统工程与电子技术,2011,33(1):89-93.
[2]付兴方,李继军,李宗植.基于两级供应关系的可修复航材存储策略模型研究[J].系统工程理论与实践,2004,24(4):111-115.
[3]范浩,贾希胜,贾云献,等.基于遗传算法的备件两级优化建模与仿真研究[J].系统工程与电子技术,2006,28(1):150-152.
[4]刘喜春,郑华,仲辉,等.备件配置优化问题研究[J].系统工程与电子技术,2008,30(10):1934-1937.
[8]阮昊智,李庆民,李承,等.改进的分层边际算法优化备件的初始配置方案[J].兵工学报,2012,33(10):1251-1257.
[9]罗袆,阮曼智,李庆民.任意结构下可修复备件的配置方案优化[J].系统工程与电子技术,2012,34(9):1866-1872.
[10]王正元,宋建社,何志德.一种备件多级库存系统的仿真优化模型[J].系统仿真学报,2007,19(5):1003-1007.
[11]王睿,彭英武,李庆民.面向动态任务的作战单元两等级两层级可修复备件优化[J].系统工程与电子技术,2013,35(4):761-769.
[12]聂涛,盛文,王晗中.装备备件两级闭环供应链库存优化与分析[J].系统工程理论与实践,2010,30(12):2309-2314.
[13]张建宇,韩国柱,陈明.武器系统备件储备量的遗传算法求解[J].军械工程学院学报,2005,17(3):36-38.
Research on Two-echelon Storage System Configuration Optimizing Based on Torpedo Equipment Spares Relation
WEI Yong,MU Lian-yun
(Navy Submarine Academy,Qingdao 266042,china)
Echelon system optimizing is an important approach to improve operational readiness and reduce life cycle cost for equipments.Through analyzing the two-echelon system for LRU and SRU spare parts of complex equipment,under a given spares configuration scheme,a calculating model of spares out of stock is proposed.Then spares configuration models of a two-echelon system is built based on spare parts contained relation.This model aims to save the spares configuration cost and avoid waste of resources through optimizing the spares configuration structure and generating a better spares configuration scheme.
two-echelonsystem,optimal configuration,spareparts,containedrelation
TP301
A
1002-0640(2016)10-0043-05
2015-08-19
2015-09-18
军队装备维修改革基金资助项目(2013825)
魏勇(1979-),男,河北沧州人,博士,讲师。研究方向:综合保障理论与技术。
