基于矢量合成的相干信号干涉仪测向模型

石　荣，李　潇，刘　畅

(电子信息控制重点实验室,　成都 610036)



·信号处理·

基于矢量合成的相干信号干涉仪测向模型

石荣，李潇，刘畅

(电子信息控制重点实验室,成都 610036)

基于通道间相位差测量的传统干涉仪测向模型在对相干多信号进行测向时会产生较大的误差，甚至测向失效，在分析其失效原因的基础上，利用相干多信号矢量合成方法，根据干涉仪基线几何结构，构建了新的相干信号干涉仪测向模型，并详细讨论了模型的求解过程。该模型不仅能够对相干多信号实施测向，而且通过对求解结果的分析可推断产生相干效应的信号个数，也能实现对传统单信号的测向，即具有较好的向下兼容性。最后通过仿真验证了模型的有效性，从而为干涉仪测向理论的发展和抗干扰应用提供了重要参考。

干涉仪；相干多信号；矢量合成；信号个数判断；测向模型；向下兼容性

0　引　言

采用干涉仪对射频信号的来波方向进行测量在射电天文、电子对抗和频谱监测等领域获得了十分广泛的应用，这其中所使用的测向模型大多以干涉仪各通道间的相位差测量为基础，从而使得在同一个工作频率上瞬时只能对一个信号实施测向。如果有两个或两个以上的同频复制的信号同时到达干涉仪，它们相互之间就会产生干涉，通常称之为相干信号。传统干涉仪测向模型在对相干信号进行测向时，通常会产生较大的误差，甚至完全失效。利用此现象文献[1]提出对干涉仪的测向过程实施相干干扰，从而达到扰乱电子侦察系统的目的。到目前为止虽然有大量的文献针对阵列天线对相干信号的测向问题进行过研究与讨论，所提出的方法主要包括：基于空间平滑的各种MU-SIC多重信号分类算法[2-5]、基于各种去相关的ESPRIT旋转不变子空间算法[6-9]、基于DFT离散傅里叶变换及变参考阵元特征法[10]、基于虚拟阵列的算法[11]、基于压缩感知的方法[12]等。但是，上述文献中所提出的方法如何在干涉仪测向中进行应用并没有相关的分析与探讨。

针对这一问题，本文分析了传统干涉仪测向模型在对相干信号测向时产生失效的原因，在此基础上利用同时到达干涉仪的多个相干信号具有相同频率这一特点，采用多信号矢量合成方法，建立了新的理论模型，通过对其求解结果的分析，可以对同时到达干涉仪的相干信号的个数进行推断。如果判定的结果是当前到达干涉仪的信号个数只有一个时，该模型所得测向结果与传统针对单信号的干涉仪测向模型所得结果完全一致，所以该模型具有较好的向下兼容性。相关的理论分析和仿真验证详细阐述如下。

1　传统干涉仪测向模型

假设在所关注的时段内干涉仪只接收到一个信号S1(t)，其波长为λ，从与天线视轴夹角为θ1的方向到达测向天线A和B，两天线之间的距离为d，如图1所示。

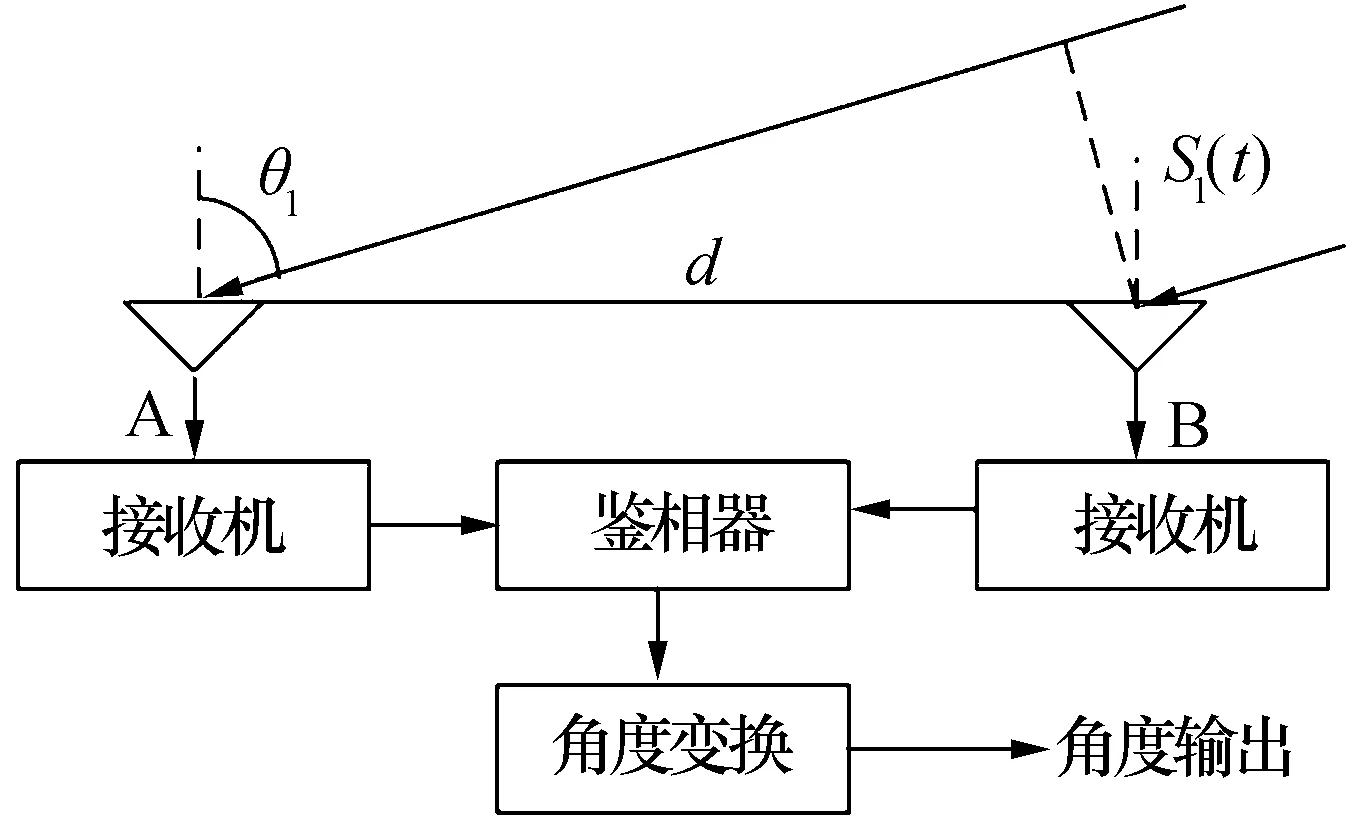
图1　单基线干涉仪测向

于是干涉仪两个接收通道中的信号分别为

SA,1(t)=a1·sin(2πfct+φ1)+nA(t)

(1)

SB,1(t)=a1·sin(2πfct+φ1+φAB,1)+nB(t)

(2)

式中：fc为信号的载波频率；φ1为初始相位；a1为信号幅度；φAB，1为信号S1(t)到达两天线的路径不同而引起的相位差；nA(t)与nB(t)分别是两个接收通道引入的噪声。在一定信噪比条件下，由式(1)、式(2)可求解出φAB，1，于是信号的来波方向θ1为

(3)

由式(3)可知，在单基线干涉仪测向应用中为了避免相位差测量过程中的相位模糊，要求d≤λ/2。如果需要进一步提高测向精度，可使用多基线干涉仪，即用长基线获得较高精度的相位差测量值，用短基线来解相位差模糊。但无论干涉仪的长短基线如何设计，传统求解方法仍是通过通道间信号的相位差测量来实现的。

2　在相干信号条件下传统模型的失效性分析

对于单频正弦波信号而言，当两个信号具有相同频率时，这就成为一对相干信号。如果相干信号S1(t)与S2(t)同时到达干涉仪的测向天线A和B，且其来波方向分别为θ1和θ2，如图2所示。

图2　干涉仪对两个同时到达信号的测向

此情况下干涉仪两接收通道中的信号分别表示为

SA，2(t)=a1·sin(2πfct+φ1)+

a2·sin(2πfct+φ2)+nA(t)

(4)

SB,2=a1·sin(2πfct+φ1+φAB,1)+

a2·sin(2πfct+φ2+φAB,2)+nB(t)

(5)

式中：φ2为信号S2(t)的初始相位；a2为其幅度；φAB,2为信号S2(t)到达两天线的路径不同而引起的相位差。由式(3)可知φAB,1和φAB,2由下式所决定

φAB,1=2πdsin(θ1)/λ

(6)

φAB,2=2πdsin(θ2)/λ

(7)

实际上这两个相干信号在同一个接收通道内可以合成一个稳定的同频信号，即

SA,2(t)=a1·γA·sin(2πfct+φA)+nA(t)

(8)

SB,2(t)=a1·γB·sin(2πfct+φB)+nB(t)

(9)

式中：γA、γB分别为A、B通道中信号相干合成后的幅度变化系数；φA、φB分别为信号相干合成后的相位，上述四个参数可由式(4)、式(5)计算如下

(10)

(11)

(12)

(13)

由上可见，在两个相干信号合成之后干涉仪两个通道所接收到的合成信号的幅度在大多数情况下是不相等的，即γA≠γB；另一方面，干涉仪两个通道所接收到的合成信号之间的相位差φAB,T为

φAB,T=φA-φB

(14)

在两个相干信号到达角不相同时，相位差φAB,T既不等于φAB,1，也不等于φAB,2。显然利用φAB,T来推算出的来波方向角既不等于θ1，也不等于θ2。虽然上述分析是以单基线干涉仪为基础进行的，但对于多基线干涉仪来说，上述分析流程同样适用，所以传统干涉仪测向方法对两个相干信号的测向错误在理论上就是不可避免的。

3　基于矢量合成的相干多信号干涉仪测向模型

实际上由式(4)、式(5)所表达的相干信号的时域信号模型可知，相干信号具有相同的载频fc，如果将时域信号模型转换为复平面上的矢量信号模型，虽然每一个信号矢量都以相同的角速度2πfc绕原点旋转，但各个信号矢量的相对位置关系是保持不变的，在复平面上以信号的幅度和相位为基础，将产生相干的N个信号Si,c表示成复矢量形式如下

Si,c=ai·exp(jφi) ，i=1,2,…,N

(15)

式中：ai表示第i个信号的幅度；φi表示第i个信号到达干涉仪中参考单元天线时的相位，如图3所示。

图3　第i个信号到达干涉仪的方位关系图示

图3中的1#天线为参考天线单元，θi是第i个信号Si(t)的来波方向与干涉仪法向之间的夹角，d1k表示1#天线单元与k#天线单元之间的距离。于是所有相干信号在1#天线处所合成的综合信号矢量S1,z可以表示为

(16)

同理，所有相干信号在k#天线(k=2, 3, …,M，M为干涉仪单元天线的总数)处所合成的综合信号矢量Sk,z可以表示为

(17)

式(17)中的附加相位项是由于信号到达不同天线单元时的延迟所产生的。为了形成统一的数学表达式，可从形式上定义1#天线与其自身的距离d11=0，于是基于矢量合成的相干多信号干涉仪测向理论模型可统一表示为

k=1,2,…,M

(18)

式中：nk为第k#天线测量时所引入的噪声矢量。

4　测向模型的求解及相干信号个数的判断

在式(18)所表达的模型中待求解的未知数的个数为3N；而方程的个数为2M，在不考虑通道噪声影响的情况下，满足如下条件时该模型才有解

2M≥3N

(19)

(20)

式中：‖·‖p表示p范数，在p=2时，式(20)则表示均方误差最小，diff(k)表示第k#天线单元对最终解所引入的噪声影响项，即

(21)

显然满足式(20)的最优解可通过对整个解空间进行优化搜索的方法来得到。但上述求解过程中，还隐含了一个假设，即已知同时到达干涉仪的相干信号的个数N。实际上在求解式(20)之前，N是一个未知数，因为我们并不知道所得到的测量数据中究竟有多少个相干信号。所以在求解该式之前，需要利用式(19)对N的上限值Nmax做一个估计

Nmax≤⎣2M/3」

(22)

式中：⎣X」表示不超过X的最大整数。首先，假设有Nmax个相干信号同时到达干涉仪；然后，对式(20)进行求解，即可得到Nmax个信号参数解集合{ai,φi,θi|i=1,2,…,Nmax}。在此基础上，对上述Nmax个解按照对应的信号幅度ai的大小由大至小排序如下

aj1≥aj2≥…≥ajNmax

(23)

如果在上述信号个数推断过程中，直接得到的结果是Nth=1，这说明此时干涉仪所接收到的是单信号。在此条件下既可按照传统的通道间相位差测量方式来获得该信号的来波方向，也可以通过求解式(20)来获得该信号的来波方向，在此情况下两种方法所得到的解应具有一致性。这也同时说明，新模型相对于传统模型来讲，更具有普适性，同时对传统模型也具有向下兼容性。

5　仿真验证

在如下仿真过程中采用(幅度，初相，来波方向)的三元组形式来进行信号参数和求解结果的描述，其中幅度为相对值，初相以到达干涉仪第一个单元天线位置处为参考，来波方向以与干涉仪天线阵的法向夹角来表达。

1)干涉仪对两个相干信号的测向

仿真条件：一维干涉仪由5个单元天线组成，它们之间的间距分别为0.05m，0.20m，0.80m，3.00m，两个信号的载波频率均为3GHz，其信号参数分别以三元组形式表示为(1.0，40°，50.1°)，(1.6，110°，19.9°)，如图4所示。

图4　干涉仪及两相干信号来波方向示意图

按照前文所提出的信号矢量表示方法，以1#天线作为参考天线，可以测量得到在五个单元天线处的综合信号矢量如图5所示。

图5　干涉仪五个天线所测得的双信号合成矢量图示

图5中各信号矢量均添加了标准差为0.02的高斯白噪声。根据式(22)，在此条件下最多可实现三个相干信号的测向。于是首先假设三个不同方向的同频信号同时到达，采用式(20)进行求解。由于整个解空间比较大，所以在求解搜索策略上采用了由粗至精的两步搜索法，粗搜索的步进较大，幅度步进为0.25，相位步进为30°，来波方向步进为5°。通过粗搜索可得到几个候选结果，其中一个表示为(1.5，120°，20°)；(1，30°，50°)；(0.25，60°，15°)。在几个候选结果附近区域都做精搜索，精搜索的幅度步进为0.1，相位步进为5.0°，来波方向步进为0.2°。通过精搜索所得到的结果为(1.6，115.0°，20.0°)；(1.1，35.0°，50.2°)；(0.1，55.0°，15°)。

上述结果是在三个同时到达的相干信号假设条件下得到的，其信号幅度值分别为1.6，1.1，0.1。前两个数值明显大于第三个，且第三个值趋近于零，由此判断：所接收到的相干信号的个数为2。在此条件下，采用两个信号的合成模型再对式(20)进行求解，最终可得这两个相干信号的来波方向分别为19.88°，50.02°；误差分别为-0.02°，-0.08°。

2)干涉仪对单信号的测向

除了信号个数减少至一个之外，即信号参数为(1.0，40.0°，50.1°)，其他仿真条件同前。同样可测量得到五个综合信号矢量如图6所示。

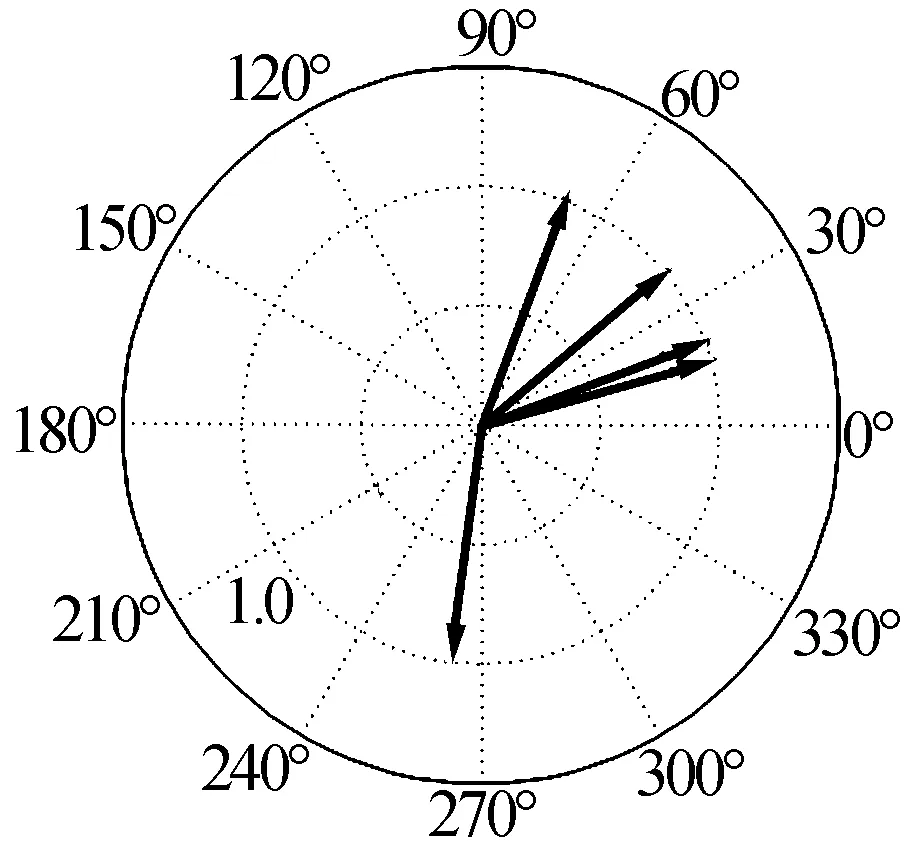
图6　干涉仪五个天线所测得的单信号矢量图示

由图6可见，五个信号矢量的幅度几乎全部一样，这也满足单信号到达干涉仪时的特征。同样通过解空间搜索，得到的结果以三元组形式表示为(1.0，40.0°，50.0°)，(0，0，0)，(0，0，0)。显然此时只有一个信号到达干涉仪天线阵。在一个信号条件下，再对式(20)进行求解，从而可得该信号的来波方向为50.09°，误差为-0.01°。

6　结束语

本文针对干涉仪应用中的相干多信号测向问题，提出了一个新的基于矢量合成的理论模型，该模型消除了传统的基于通道间相位差计算而带来的相干信号情况下的测向失效条件，通过解空间搜索优化方法可直接求解出各个相干信号的来波方向。在求解过程中，不仅可实现对相干信号个数的推断，而且还能得到产生相干的各个信号的幅度大小和相对相位值。另一方面，该模型对单信号测向同样适用，所以相对于传统方法来说具有向下兼容性。相关的仿真结果也印证了理论分析的有效性。虽然本文对相干信号源建模时以单频信号为对象展开讨论，实际上对于调制信号，如相位编码、调频信号等，在对信号幅值与初相参数测量之后，也可采用此方法进行测向。综上所述，本文从理论和仿真上对基于矢量合成的相干信号干涉仪测向方法进行了分析，后续还需继续开展应用方面的研究工作，以解决工程中相关的应用性问题。

[1]杨军佳, 毕大平, 陈慧. 相位法测向系统相干干扰效果分析[J]. 电子信息对抗技术, 2012, 27(6): 47-49.

YANG Junjia, BI Daping, CHEN Hui. Coherent jamming effect analysis on interferometer[J]. Electronic Information Warfare Technology, 2012, 27(6): 47- 49.

[2]司锡才，甄佳奇，那振宇. 二维相干信号测向估计方法[J]. 系统工程与电子技术, 2009, 31(8): 1982-1984.

SI Xicai, ZHEN Jiaqi, NA Zhenyu. Approach to 2-D angles direction estimation for coherent signals[J]. Systems Engineering and Electronics, 2009, 31(8): 1982-1984.

[3]肖雷，管振辉，杨春华. 基于MUSIC算法对相干信号DOA估计的研究[J]. 舰船电子对抗, 2010, 33(6): 114-117.

XIAO Lei, GUAN Zhenhui, YANG Chunhua. Research into the DOA estimation of coherent signals based on MUISC algorithm[J]. Shipboard Electronic Countermeasure, 2010, 33(6): 114-117.

[4]吴小强，刁鸣，缪善林. 基于内插阵列变换的相干源测向方法研究[J]. 应用科技, 2007, 34(2): 1-4.

WU Xiaoqiang, DIAO Ming, MIAO Shanlin. Study on DOA estimation of coherent sources based on interpolated array transformation[J]. Applied Science and Technology, 2007, 34(2): 1-4.

[5]张聪，胡谋法，卢焕章. 基于虚拟阵列空间平滑的相干信号DOA估计[J]. 电子学报, 2010, 38(4): 929-933.

ZHANG Cong, HU Moufa, LU Huanzhang. Virtual array-based spatial smoothing method for direction finding of coherent signals[J]. Acta Electronica Sicinca, 2010, 38(4): 929-933.

[6]何劲，嵇玮玮，刘卫平，等. 基于线性tripole阵列的相干信号角度和极化估计与跟踪[J]. 上海航天, 2015, 32(1): 17- 21.

HE Jin, JI Weiwei, LIU Weiping, et al. Angle-polarization estimation & tracking for coherent signals using a linear tripole array[J]. Aerospace Shanghai. 2015, 32(1): 17-21.

[7]甄佳奇，司锡才，王桐，等. 基于虚拟阵列的相干信号快速测向算法[J]. 吉林大学学报(工学版), 2010, 40(3): 848-851.

ZHEN Jiaqi, SI Xicai, WANG Tong, et al. Fast approach for direction estimation coherent signals based on virtual array[J]. Journal of Jilin University (Engineering and Technology Edition), 2010, 40(3): 848-851.

[8]张辉，葛临东. 利用时间平滑技术估计相干信号二维波达方向[J]. 信息工程大学学报, 2007, 8(1): 68-71.

ZHANG Hui, GE Lindong. UCA based 2-D DOA estimation of multi-source multipath signals[J]. Journal of Information Engineering University, 2007, 8(1): 68-71.

[9]杜刚，张永顺，姜新迎. 相干信号源的空时三维参数分离估计方法[J]. 现代雷达，2008, 30(3): 67-69, 73.

DU Gang, ZHANG Yongshun, JIANG Xinying. Space-time three-dimension parameter separable estimation method of coherent signals[J]. Modern Radar, 2008, 30(3): 67-69, 73.

[10]林亭，曾新吾，孙海洋. 离散傅里叶变换及变参考阵元特征法在相干信号估计中的应用[J]. 信号处理, 2012, 28(3): 404-409.

LIN Ting, ZENG Xinwu, SUN Haiyang. DFT and shift reference sensor method applied in coherent signal parameter estimation[J]. Signal Processing, 2012, 28(3): 404-409.

[11]甄佳奇，丁群，赵冰. 虚拟阵列下的相干信号测向算法[J]. 系统工程与电子技术, 2013, 35(10): 2032-2035.

ZHEN Jiaqi, DING Qun, ZHAO Bing. Direction finding algorithm for coherent signals by virtual array[J]. System Engineering and Electronics, 2013, 35(10): 2032-2035.

[12]刁鸣，安春莲. 独立信号与相干信号并存的二维DOA估计新方法[J]. 西安电子科技大学学报(自然科学版), 2013, 40(5): 66-71,98.DIAO Ming, AN Chunlian. 2-D DOA estimation of coexisting uncorrelated and coherent signals[J]. Journal of Xidian University(Natural Science), 2013, 40(5): 66-71,98.

石荣男，1974年生，博士，研究员。研究方向为电子对抗，雷达与通信系统等。

李潇女，1993年生，硕士研究生。研究方向为电子对抗。

刘畅女，1988年生，硕士。研究方向为电子对抗。

Direction Finding Model for Coherent Multi-signals by Interferometer Based on Vectors Composition

SHI Rong，LI Xiao，LIU Chang

(Science and Technology on Electronic Information Control Laboratory, Chengdu 610036, China)

The conventional direction finding model by interferometer is based on the phase difference measurement among its channels. When it is used for the coherent multi-signals, there are huge errors and even failure sometimes. After the reason is given for this problem, the direction finding novel model for coherent multi-signals by interferometer is established for geometric configuration of its baselines, utilizing the method of vectors composition. Then the resolving method is discussed in detail. Not only the direction of coherent multi-signals can be found, and the number of signals is deduced by the result analysis, but also it is feasible for the single signal. Its compatibility downward is good for the conventional processing. The validity of this model is demonstrated by the simulations in the end. It is important for the development of direction finding theory and anti-jamming application of the interferometer.

interferometer；coherent multi-signals；vectors composition；deducing number of signals；direction finding model；compatibility downwards

10.16592/ j.cnki.1004-7859.2016.09.005

石荣Email：wyx1719@sina.com

2016-04-20

2016-06-22

TN971

A

1004-7859(2016)09-0023-05