高速公路连拱隧道出入口过渡段长度设计的探讨
2016-11-15宋俊涛
宋俊涛
(山西省交通科学研究院,山西 太原 030006)
1 概述
随着山区高速公路快速发展,桥梁、隧道等构造物逐渐增多。在公路设计过程中,根据山区公路的地形特点、围岩条件、施工方法、支护时间、占地大小、环境影响和工程造价等因素的影响,隧道设置类型也不同[1]。在高速公路穿越垭口、鸡爪沟等地形时,当路堑的开挖深度大于40 m,并且设置分离式隧道困难,或者设置分离式隧道需要增加较大的工程量时,就可以考虑采用连拱隧道。采用连拱隧道能够维持自然景观不被破坏和可以避免高边坡的不稳定对运营造成的安全隐患。并且采用连拱隧道的线形指标要求较低,线形布设方便,接线工程数量小且线形较为顺畅[2]。在连拱隧道设计过程中,要充分考虑到连拱隧道并行双洞的相互影响,为了保证连拱隧道安全,必须设置能够满足要求厚度的中隔墙,从而导致隧道段中央分隔带的宽度与一般整体式路基的中央分隔带宽度不一致,隧道出入口行车环境发生了较大的变化,大大降低了隧道行车的安全性[3]。根据公路隧道设计规范要求,隧道洞口外与之相连的路段应设置距洞口不小于3 s设计速度行程长度,且不小于50 m的过渡段,在满足车道行驶轨迹的条件下,保持公路断面过渡的顺适[1]。设置合理过渡段长度的连拱隧道出入口,则可保证驾驶人驾驶车辆在进出隧道前后视觉的连续性和车辆安全行驶速度变化的需求[4]。因此,本文针对设计中隧道中隔墙宽度不同,设计速度不同的隧道出入口过渡段长度进行计算,以期在设计过程中得到隧道出入口过渡段合理长度。
2 行车轨迹分析
在高速公路行驶的车辆,驾驶人根据道路几何线形的诱导作用,在各自的行车道上按规定速度行驶,进入连拱隧道前后,由于隧道横断面与路基的横断面不一致(见图1),行车道的线形发生变化,从而导致汽车的行车轨迹发生变化。
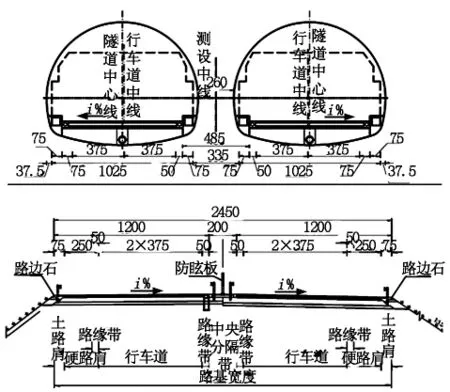
图1 80 km/h高速公路连拱隧道与整体式路基横断面对比示意图(单位:cm)
2.1 换道分析
汽车在行驶过程中,驾驶员通过转动方向盘,使得车辆发生转向,从而完成换道操作。隧道进出口车辆的行车轨迹决定了渐变行为的持续时间,根据Worrall等人的研究成果,车辆在行车道发生变化或者换道行驶时,调整行驶过程分为3个阶段,见图2[5]。因此,隧道出入口缓和段的行车轨迹可以简化为汽车换道行驶进行分析。

图2 车辆换道示意图
2.2 相关参数分析
通过查阅相关资料,驾驶人驾驶车辆在经过隧道出入口或者当行车道线形发生变化时,车辆的变道行驶轨迹为一条曲率连续变化的缓和曲线,如果将车辆换道行驶的第二阶段以刚刚跨越行车道边线为界,将行车轨迹划分为两个阶段(见图3),第Ⅰ、Ⅱ两阶段之间是通过回旋线将两个反向圆曲线径向连接的S曲线,且两回旋线长度之比为1∶1。在第Ⅰ阶段和第Ⅱ阶段中,车辆的运行轨迹为两条连续且同向的曲线,该曲线是一条通过回旋线径向连接而形成的卵形曲线。基于车辆换道行驶的轨迹特征,缓和曲线轨迹与车辆逐渐转动方向盘的运行轨迹吻合,此时Ⅰ、Ⅱ阶段中的两卵形曲线可以分别等分为两段等长的同向缓和曲线,则相连处的圆曲线半径为该速度下的最小安全转弯半径[6]。首先,确定圆曲线的最小转弯半径,然后根据测量学[7]中带有缓和曲线的平曲线测设中的内容,利用缓和曲线变道轨迹进行计算,从而得出缓和段的长度。
2.2.1 圆曲线最小转弯半径的确定
根据《公路工程技术标准》中4.017~4.018条的规定,圆曲线最小半径以汽车在曲线部分能够安全而顺畅地行驶所需的条件而确定的。圆曲线最小半径的实质是汽车行驶在公路曲线部分时,所产生的离心力等横向力不超过轮胎与路面的摩阻力所允许的界限[8]。根据车辆在弯道行驶时的受力状况及各种力的几何关系,得出公式(1):

式中:R为圆曲线半径,m;V为设计速度,km/h;μ为横向力系数,见表1;ih为超高值。
车辆变道行驶与正常行驶过程的不同之处在于存在反超高,并且以存在反超高为最不利情况,在该情况下的半径为最小安全半径。通过计算可以得出,不同速度下的最小转弯半径,见表1。
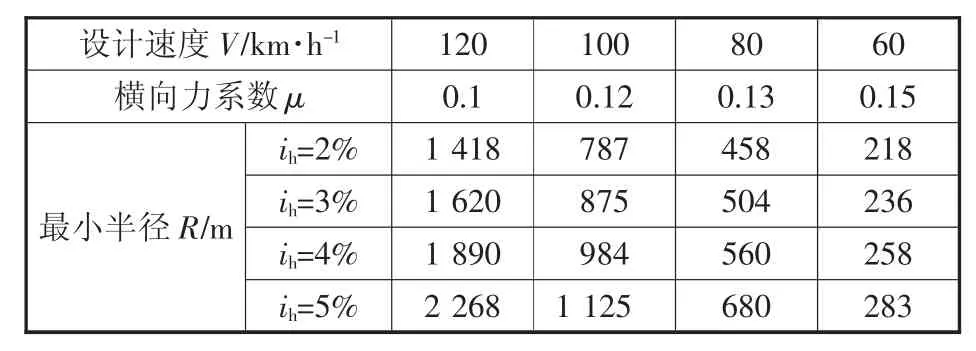
表1 不同设计速度下最小安全转弯半径
2.2.2 运行轨迹方程相关参数确定

图3 运行轨迹示意图
如图3所示,设汽车前进的方向为X方向,垂直方向为Y方向,则在换道行驶的过程中,ΔY为汽车侧向移动距离,ΔX为前进方向行驶距离。
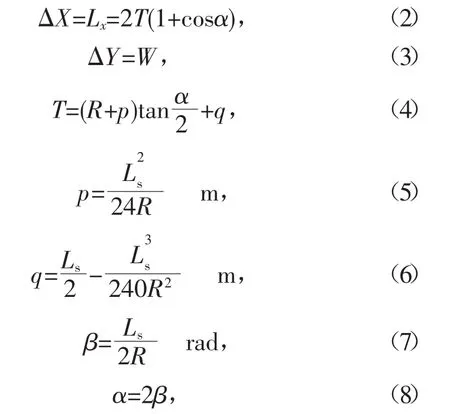
式中:T为切线长;p为内移距;q为切线增值;Ls为缓和曲线长,m;β为缓和曲线角。
假设汽车在移动过程中保持匀速行驶,那么由式(2)~式(8)可以得到:
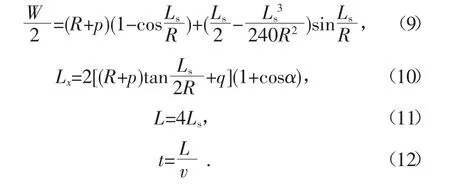
式中符号同前,其中L为汽车实际运行距离;t为汽车换道行驶时间;v为设计速度。
2.3 过渡段长度计算模型
以山西某高速公路连拱隧道为例,该高速公路设计速度80 km/h,整体式路基中央分隔带宽度2 m,整体式路基中央分隔带与连拱隧道中隔墙相接,中隔墙、检修道合计4.85 m(图1),为保证行车的连续性,应将连拱隧道前后一段范围内设置缓和段,将中央分隔带的宽度由2 m渐变至4.85 m,使得隧道断面中隔墙和检修道组成的中央分隔带完全与整体式路基横断面相对应。在设计中采用两侧对称渐变的方式进行隧道缓和段渐变设计,如图4所示。汽车行驶轨迹随着行车道的变化而变化,其变化宽度为横断面变化的一半。假设中央分隔带宽度变化值为ΔW,则ΔY=ΔW/2,利用2.2中相关公式,可以得出:

解方程得到 Ls,根据公式(11)、(13),可以得出车辆换道行驶前进距离L,即所求缓和段长度的最小值,本例计算缓和段长度为80 m。

图4 隧道出入口过渡段设计示意图
3 过渡段长度计算值
通过上文的分析计算,可以得出不同设计速度,不同中隔墙宽度的连拱隧道出入口过渡段长度,见表2。
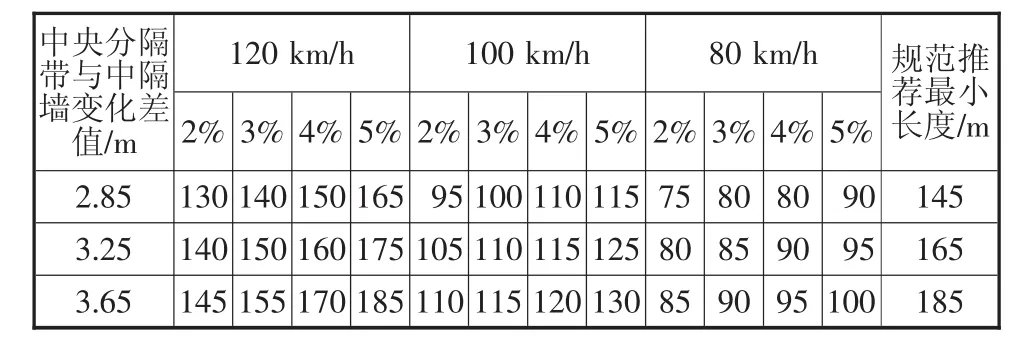
表2 不同设计速度渐变段计算长度及规范规定推荐最小值
由计算结果可以看出,以设计速度80 km/h,中央分隔带与中隔墙之差为2.85 m的连拱隧道缓和段为例,当隧道进出口位于半径为850 m的圆曲线上时,圆曲线超高为4%,通过计算可以得出最小安全转弯半径为560 m,所需渐变段长度为80 m,渐变所需要的时间为3.6 s。《公路路线设计规范》要求,当中间带的宽度增宽或减窄时,应设置过渡段,过渡段的渐变率不应大于1/100[9]。当连拱隧道的中隔墙厚度为2.85 m时,一侧的变化宽度为1.425 m,根据规范要求1/100的渐变率进行计算,可以得出,渐变段长度取145 m(145 m>80 m),即满足规范要求的渐变段长度大于车辆在隧道出入口变道所需的最小长度。因此在设计中应将两者的计算结果进行对比,选择较大值作为隧道出入口缓和段长度取值。
4 结论
本文通过对行车轨迹的分析,对隧道进出口过渡段的长度进行验算分析,得出如下结论,为相关设计提供参考。
a)设计速度不同,渐变段长度不同,速度越大,所需过渡段长度越长;在同一设计速度的情况下,中隔墙宽度越大,缓和段长度越长;连拱隧道所在的平曲线半径越小,即超高值越大,过渡所需缓和段长度越长。
b)为保证隧道过渡段的行车安全,过渡段长度取值应不小于采用本文方法计算的长度与规范要求值中的较大值。
