基于LMS的自适应陷波器的设计与实现

陈颉

（安康学院 电子与信息工程学院，陕西 安康 725000）

基于LMS的自适应陷波器的设计与实现

陈颉

（安康学院 电子与信息工程学院，陕西 安康 725000）

自适应陷波器是一种特殊的滤波器，它能够通过不断地自我学习和调整使系统始终工作在最佳状态。本文针对一般陷波器的缺陷，在LMS算法的基础上，设计了自适应陷波器，并通过M atlab编程实现了抑制单频干扰和双频干扰的自适应陷波器。系统测试结果表明，合理选择收敛因子值，可以使自适应滤波器具有优良的滤波特性。该研究为微弱信号检测以及消除各种通信系统中的窄带干扰提供了参考价值。

一般陷波器；自适应陷波器；LMS算法；自适应干扰对消

随着通信技术的应用越来越广泛，通信系统对滤波器精度的要求也越来越高[1-2]。当通信系统遭遇功率较大的窄带信号干扰时，该系统将无法正常工作，这时必须借助某种滤波技术削弱这种干扰[3-4]。一般陷波器陷波频率固定，无法跟踪窄带干扰频率，很难适应复杂的环境变化，因此笔者提出一款利用自适应理论和相关技术设计的自适应陷波器以滤除干扰。自适应陷波器是一个可以自动调节其特征的数字滤波器，它根据输入信号自动地变化，特别适合于滤出频率在一定范围内随机变化，且与信号的频谱在同一范围内的干扰波[5-6]。本文研究和改进了一般陷波器，并通过Matlab编程设计和实现了自适应陷波器。

1　系统设计

自适应陷波器的频率响应具有按照某些准则自动改变以提高其性能的性质，使滤波器根据输入信号的特性而改变。其特性变化是由自适应算法通过调整滤波器系数来实现的[7]。

1.1LMS自适应算法研究

一般梯度估值的自适应算法，需要分别取权值经扰动后的两个均方误差估值之差作为梯度的估值。LMS算法（Least Mean Square，即最小均方算法）避免了一般梯度估值带来的弊端，它简单地直接利用单次采样数据误差的平方e2（n）替代E｛e2（k）｝的估计。于是其自适应过程每次迭代中的梯度估值如下：

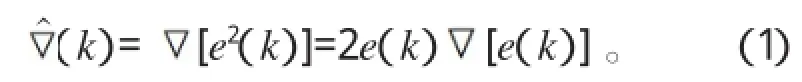
于是有

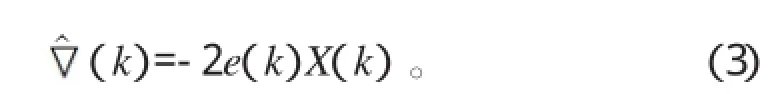
LMS自适应算法最终可改写为：

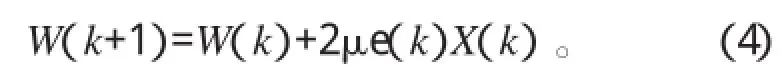
LMS算法有两个关键：梯度（k）的计算及收敛因子的选择。LMS算法流程图如图1所示。

图1　LMS算法流程图

1.2自适应陷波器设计

自适应陷波技术来源于自适应噪声抵消，它设定一个正弦信号作为参考信号，以抵消窄带噪声中的每一个分量。当用正弦波作为参考输入时，LMS算法便成为自适应陷波滤波器，它可以在中心位于参考频率附近的窄带内消除掉主频谱分量，由于自适应陷波器只有一个参数需要估计，因而算法简单，易于控制带宽、零点深度大，并且能够精确地自适应跟踪干扰频率和相位等，而且通过将极点限制在单位圆内，稳定性得到了保证[8]。

1.2.1单频干扰自适应陷波器设计

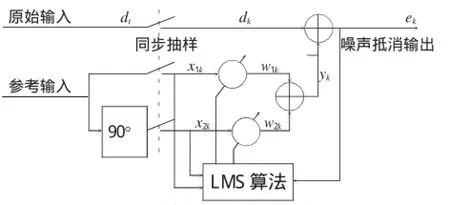
图2　单频干扰自适应陷波器

单频干扰自适应陷波器的原理框图如图2所示，它具有2个自适应权系数。原始输入是真实信号s与单色干扰n的混合波形s+n，其中噪声和信号不相关。参考输入是一个和信号不相关而和噪声相关的信号x。自适应滤波的目的是利用参考输入信号x估计噪声n。

原始输入经采样送至dk端；参考输入x经采样送至x1k端和x2k端，x2k为参考输入x经过90°相移后的采样值，其目的是获得w1k和w2k两个权，从而使组合后的正弦波振幅和相位都可以与原始输入中的干扰分量的振幅和相位相同，参考输入加权后的输出为yk，它是对噪声nk的估计。这样含有干扰频率的采样信号dk与yk相减后，就得到有用信号的最佳估值ek。

假定输入的信号形式任意，参考输入为一单频正弦波C cos（Ω0t+φ），式中Ω0为模拟信号角频率。将原始输入和参考输入以时间间隔T进行周期采样，则ω0=Ω0T为抽样信号数字角频率。采样后的参考输入可表示为式（5）：

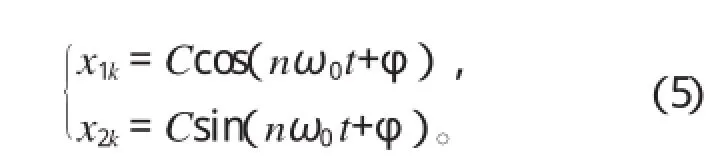
采用LMS算法进行自适应陷波时，权矢量的修正过程如下：

利用LMS算法进行迭代计算，可以得到单频干扰自适应陷波器传递函数为：

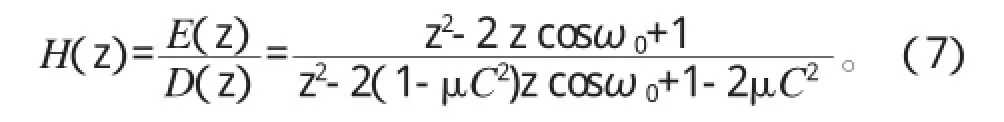
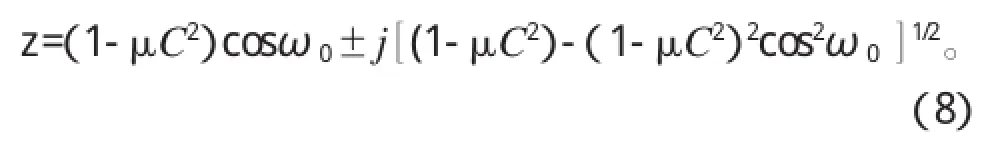
极点在单位圆内，它们与原点的径向距离为（1-μC2）1/2，近似等于1-μC2，故系统是稳定的。

由以上分析可知，当参考输入为单一频率正弦波时，即使参考频率缓慢变化，自适应过程也能保持对消的正确相位关系，因此零点的深度一般优于固定滤波器的零点深度。

1.2.2多频干扰自适应陷波器

多频干扰自适应陷波器采用并联型结构实现，并联型结构即指原始输入仍为受干扰信号，而将参考输入扩充为多个，分别都用2个权来调节振幅和相位，实现多个频率的陷波。自适应陷波器输出部分为两级陷波器的输出之和。噪声对消器的输出即为原始信号输入与此自适应滤波器输出和的差。假设干扰信号频率为ω0和ω1，参考输入即为：C0cos(ω0t+φ0)和C1cos(ω1t+φ1)，此时系统的传递函数为：

此种结构在ω0和ω1处仍具有无穷大衰减，但是由于是并联结构，极点同时与参数C0、C1、ω0、ω1有关，调节相对复杂。另一种形式为级联型结构，即第一级陷波器输出作为第二级陷波器的输入，组成级联形式。此结构可以避免并联结构的弊端，其原理框图如图3所示。

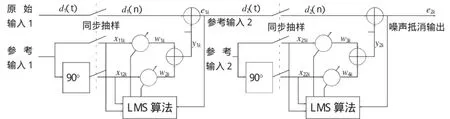
图3　多频干扰自适应陷波器

系统传递函数如下：

不难看出，系统的零极点分别是每级陷波器的零极点，可以直接改变其中某一级的调整参数而不影响另一级陷波器的零极点特性，因此采用级联型结构，不仅具有单频陷波器的优点，而且使陷波器的性能调节变得简单有效，更容易实现。

2　系统实现

2.1单频干扰自适应陷波器

单频干扰自适应陷波器设计如图4所示，原始信号经过采样后，经权值调节后输出估计信号，与期望输出量相减后，通过误差向量控制自适应算法，进而控制权值，经过多次循环以后，误差逐渐减小，权值趋于最优值，输出信号也将逼近真实信号。

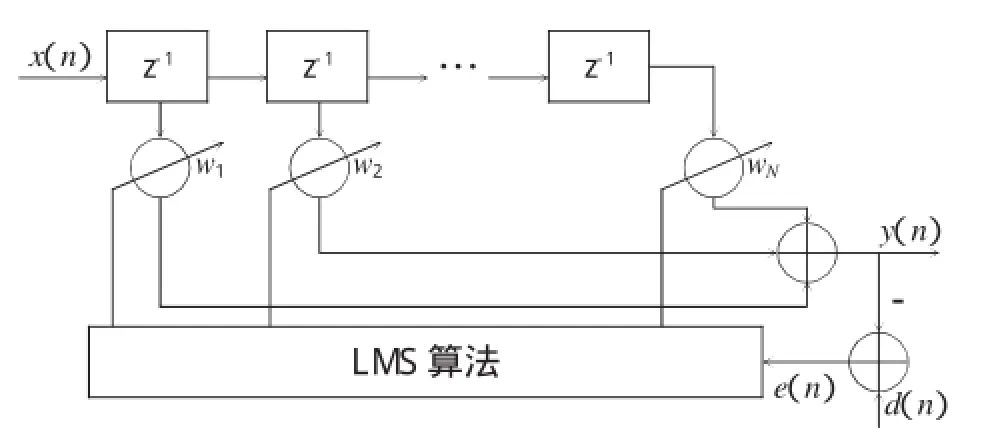
图4　单频干扰自适应陷波器流程图

以工频干扰为例，首先设定输入信号为200Hz的输入和60Hz的工频干扰信号的叠加，然后进行自适应陷波器设计，以60Hz的正弦信号作为参考信号输入，采用LMS算法进行自适应陷波，陷波后观察输入与输出的幅频特性如图5所示，可以明显看出，具有良好的滤波效果。

图5　单频干扰下滤波前后幅频特性比较

2.2双频干扰自适应陷波器

在单频干扰自适应陷波器的基础上，设计受两个频率干扰的自适应陷波器。根据图2的两个频率干扰的自适应陷波器原理，双频干扰自适应陷波器由两级单频自适应陷波器级联而成，只需将60Hz 和50Hz正弦信号分别设为两级的参考输入即可，其它算法和单频自适应陷波器相同。第一级先滤除掉60Hz的干扰，输入第二级后，再滤除掉50Hz干扰，输出信号即为有用正弦信号的估计。

输入信噪比为SNR1=5dB，采样频率fs=5000H z，采样点N=5000。信号为：s=sin（2π×200t），噪声分别为：

陷波后观察输入与输出的幅频特性如图6所示，可以明显看出，滤波效果良好。

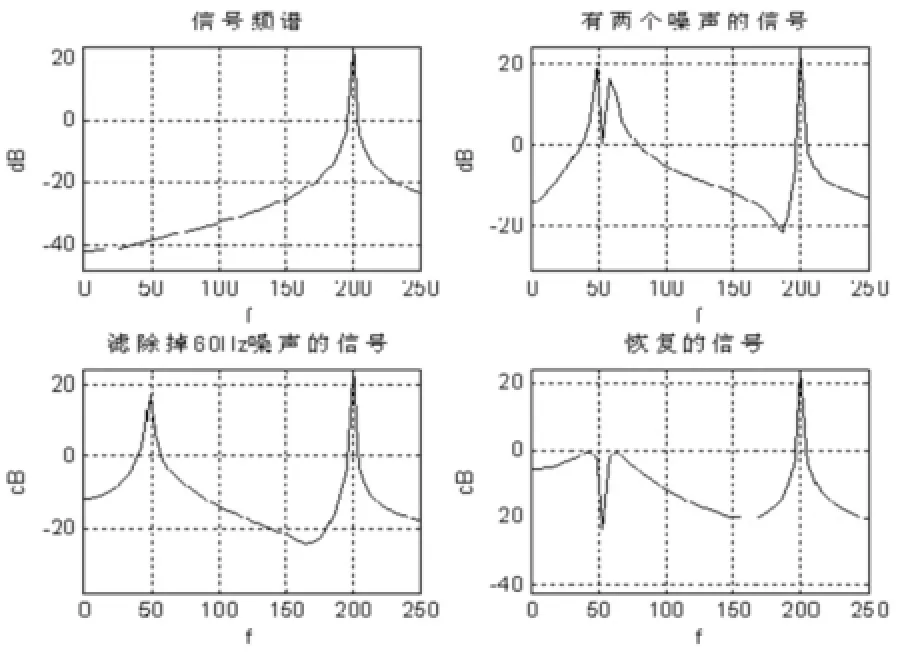
图6　双频干扰下滤波前后幅频特性比较

3　性能分析

3.1收敛因子对滤波效果的影响

修改前文设计的单频自适应陷波器的收敛因子，观察其对滤波效果的影响。结果表明，随着收敛因子的增大，需要迭代的次数减少，即收敛速度变快，但是误差将会变大。所以，设计自适应陷波器时，应根据具体情况设置收敛因子值，需在迭代次数和误差之间作出选择，权衡利弊，加以取舍。工程上，收敛因子值按如下公式选取比较合适[7]：

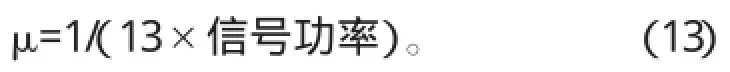
3.2信号与干扰频率差对滤波效果的影响

设置单频自适应陷波器的信号为200Hz，信噪比设为5dB，让干扰频率逐渐靠近信号频率，观察滤波效果。测试结果表明，当干扰频率靠近信号频率时，误差将变大，但是滤波效果仍然理想，当频率差仅为10Hz时，干扰衰减仍可达到15dB以上，因此干扰频率接近信号频率时，自适应陷波器仍具有良好的滤波特性。

4　结语

针对现有一般陷波器存在的缺点，笔者提出利用LMS算法设计和实现了一款自适应陷波器，并对其性能进行了测试。结果表明，这种自适应陷波器的性能优于一般陷波器。该研究对微弱信号检测以及消除影响仪器性能的工频干扰以及消除各种通信系统中的窄带干扰具有参考价值。

[1]孟庆萍，周新力，刘华芹.罗兰C接收机中窄带干扰的抑制技术[J].微电子技术，2007（22）：132-134.

[2]自适应算法[EB/OL].（2016-04-10）[2016-04-26].http：// baike.baidu.com/view/3378814.htm?fr=ala0_1.

[3]常建华，全书海.自适应陷波器的原理、应用及其算法仿真[J].武汉汽车工业大学学报，1998，20（3）：46-49.

[4]姚天任，孙洪.现代数字信号处理[M].武汉：华中理工大学出版社，1999：11.

[5]曹余庚，谢敏.自适应工频陷波器的原理与设计[J].电测与仪表，1985（11）：17-20.

[6]李勇，徐震.MATLAB辅助现代工程数字信号处理[M].西安：西安电子科技大学出版社，2002：10.

[7]刘芳芳.基于自适应陷波器的干扰抑制研究[J].应用科技，2008，35（9）：33-38.

[8]薛年喜.MATLAB在数字信号处理中的应用[M].2版.北京：清华大学出版社，2008：1.

【责任编校李林霞】

The Design and Im p lem entation of Adap tive Notch Filter Based on LM S A lgorithm

CHEN Jie
（School ofElectronics&Information Engineering，AnkangUniversity，Ankang 725000，Shaanxi，China）

Adaptive Notch Filter（ANF） is a special filter，which can make the system work in an optimal condition by continuously self-learning and adjustment.This article first introduces some related knowledge of the Adaptive Filter technology，and analyzes the general basic principle of the Notch Filter，focusing on its shortcomings；Then it investigates the theoretical basis of ANF——LMS algorithm and Adaptive Interference Cancellation；Based on the LMS algorithm，the schematic of ANF was established.And by Matlab programming，two ANF，which can respectively achieve the inhibition of single-frequency interferenceand dual-frequency interference，wereobtained.At last，itemphasizes the performances of ANF.The resultsof the performanceanalysisshow that：the reasonable choice of the value u can make the design more practical；and when the interference frequency is close to the signal frequency，the filtering effect is still good.；when the interference isnon-single frequency，the ANF still hasexcellent filtering properties；however，when the interference frequency is too strong，the ANF will notapply in the real.

General notch filter；Adaptive notch filter；LMS algorithm；Adaptive InterferenceCancellation

TN713

A

1674-0092（2016）05-0113-04

10.16858/j.issn.1674-0092.2016.05.025

2016-05-10

陈颉，男，陕西安康人，安康学院电子与信息工程学院助教，硕士，主要从事卫星导航与通信研究。