智能电网环境下多零售商的实时定价决策分析

韩精艺+代业明

摘要： 输配电价改革是我国电力体制改革的关键环节，其重要内容之一是调整电网盈利模式。文章在智能电网环境下提出多个电力零售商之间基于需求侧管理的Stackelberg博弈模型，并进行模型分析与求解，然后根据实际情况进行仿真模拟。结果表明：根据用户需求量变化反映出的信息，文章所提出的实时定价机制，不仅能够缓解电力供需矛盾，而且能为所有电力零售商提供了一种利润最大化定价策略。

Abstract： Transmition and distribution reform is the crucial aspect of the power price reform in China， and one of its important content is the earning model. The paper introduced a stackelberg model under the smart grid condition， which was based on the demand-side management between all electricity retailers， and analyzed the model and solve it， then simulate and imitate the result with datum based on the real situation. The result shows that， according to the information that reflected by the changes of consumers demand， the real-time pricing model provided by this paper not only could help releasing the contradiction between the amount of demand and supply of power， but also could provide a profit maximization strategy for electricity retailers.

关键词： 智能电网；实时定价；Stackelberg博弈；需求侧管理

Key words： smart grid；real-time pricing；Stackelberg game；demand-side management

中图分类号：F426 文献标识码：A 文章编号：1006-4311（2016）29-0080-03

0 引言

随着电器种类增多和电力需求量增大，对传统电网的挑战逐渐加剧，特别是一些发达地区的发电量已无法满足用电高峰时期的电力需求。需求侧管理（Demand-side Management，DSM）作为一种提高电网可靠性的重要机制，可通过电力需求的动态变化来优化电力基础设施的运行和管理，实时定价是DSM的重要策略之一[1-4]，通过实时告知电力用户电价，使用户根据自己的需求和意愿选择用电方式，实现用户主动调节负荷，削峰填谷，达到资源的优化配置。

近年来国内外学者对智能电网的推广应用研究已有很多[5-11]，与博弈理论结合解决了各种决策问题。当一个地区同时存在两个或多个电力零售商时，一个零售商的决策在受到了其他零售商决策影响的同时，也影响其他零售商的决策。文献[8]中未将用户的行为量化成需求函数，而是提出了一个电器水平的跟随者的博弈模型，文献[9-11]提出几种不同的实时定价算法，在保持消耗总电量低于发电能力前提下可以最大化系统总所有用户收益和最小化电力供应商成本。文献[5]中将不同区域中的不同电力零售商抽象为领头零售商和尾随零售商两类，建立相应的Stackelberg博弈模型，分析二者在智能电网实时定价中的策略互动。

然而，受电力市场改革进程影响，针对多个零售商共存在同一地区时如何制定最优的定价策略的研究依然不多，并且缺乏考虑对零售商之间价格差异如何影响用户的电力需求量。本文在文献[5]的基础上进行拓展，建立多个零售商之间一主多从的stackelberg博弈模型，研究电力市场中零售商们之间的相互影响，并通过零售商之间单位价差导致用户需求的转移量来刻画价差的影响，然后进行模型分析与求解，得到能够使各电力零售商获得的利润最大化定价策略。下面首先对基本变量进行假设，然后针对多个零售商建立一主多从的stackelberg博弈模型，之后对模型进行求解得到最优决策，最后得到相应的结论并对以后的研究方向进行展望。

1 模型准备

1.1 基本假设

定义G零售商的策略空间，即G=[p1，p2，…ph，…，pH]，其中ph代表在h时的电力价格，pH代表在H时的电力价格。同时，记先行零售商为FL，所有跟随零售商都包含在集合U中，即U=（F1，F2，…，Fn），则Fi∈U，i=1，2，…，n。

在供电量充足的条件下，假定电力用户是理性的，可以根据先行商和跟随商的定价灵活地选择使用哪一家的电力，并根据需求和成本控制做出正确的决策。电力用户可以根据智能电表上显示的某时段的电价，选择是否使用某些电器。如果用户觉得某一时段的电价太高，而某些电器是可以改变使用时间或者直接减少使用，则可以通过选择电价较低的时段来使用这些电器，并且每一个用户每次只能选择使用某一家零售商的电力。

1.2 基本函数

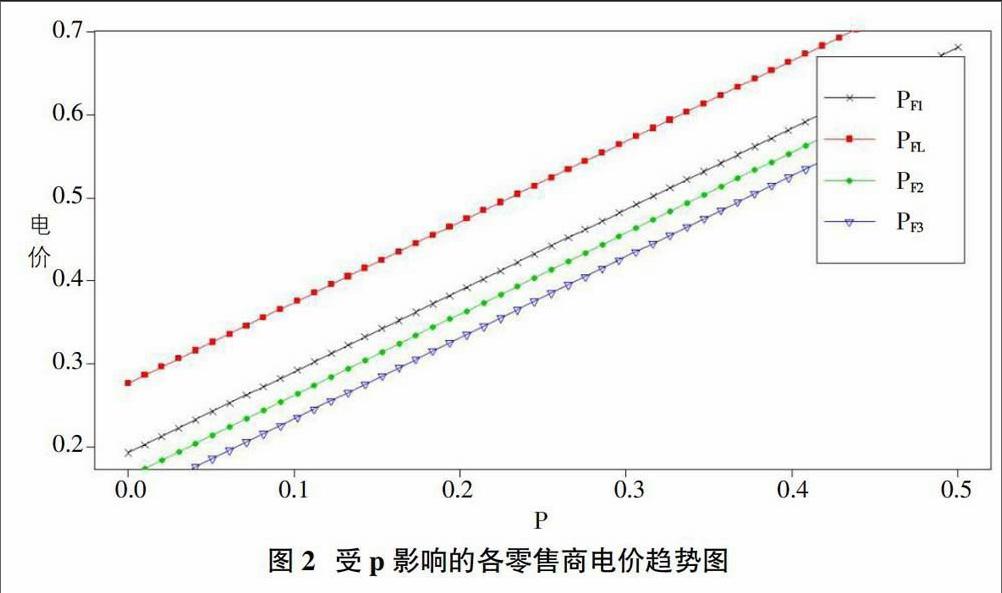
图2显示的是当各零售商的进电价p的取值区间为[0，0.5]时，各零售商的电力定价决策是如何变化的，可以看出先行者零售商制定的电价高，若进电价p越低，在同等用电量水平上成本越低，则各零售商制定的电价也会越低，同时受电价为零时用户需求量多寡的影响，各跟随者零售商之间的价格也不尽相同。

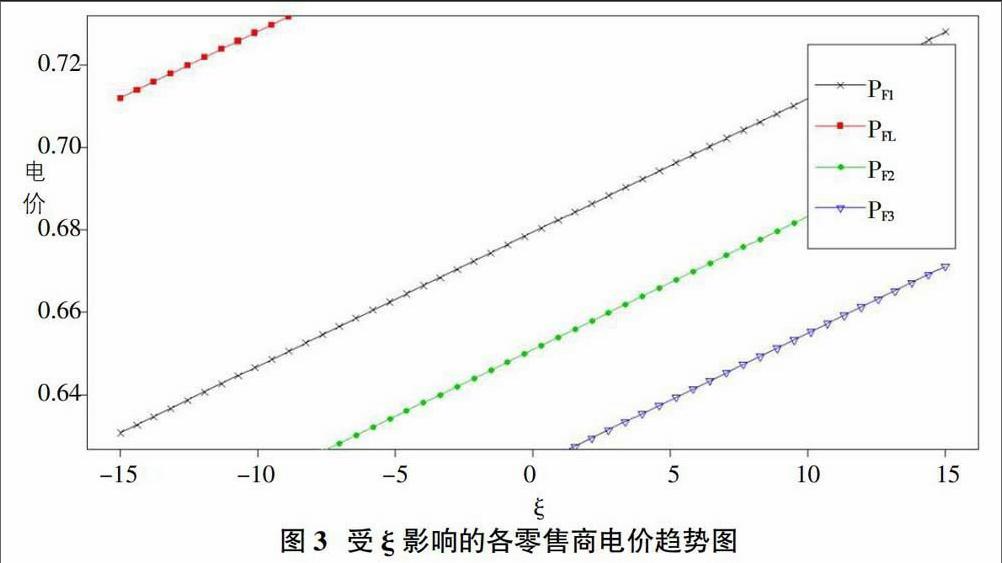
图3显示的是当各零售商的需求弹性？孜的取值区间为[-15，15]时，各零售商的电力定价决策是如何变化的，发现除了先行者零售商的电价高，需求价格弹性？孜越小，各零售商制定的电价越低，而且各零售商的电价高低也受电价为零时用户需求量多寡的影响。

3 结论和展望

本文从电力需求侧管理出发，通过对智能电网实时定价问题进行建模研究，发现电力零售商通过科学合理的实时定价可以实现利润最大化，用户可以通过智能电表和转移用电时间来有效控制用电成本，保证低收入家庭的用电需求和生活质量，同时还能有助于节能减排的实现。此外，各零售商在制定各自的电力价格时，需要考虑单位价差导致的用户需求转移量、进电价以及电力的需求价格弹性三方面因素的影响，然后制定相应的利润最大化策略。

由于本文主要是针对多个零售商之间的价格竞争进行探讨，没有考虑到不同电器分类对电力定价的影响，所以进一步的拓展研究可以向多个电力零售商和多个用户之间的互动博弈以及考虑到电器分类的影响等方向进行。

参考文献：

[1]T Jin， M Mechehoul. Ordering electricity via internet and its potential for smart grid systems[J]. IEEE transactions on Smart Grid， 2010， 1（3）： 302-310.

[2]A H Mohsenian-Rad， V W S Wong， J Jatskevich， et al. Autonomous demand-side management based on game-theoretic energy consumption scheduling for the future smart grid[J]. IEEE Transactions on Smart Grid， 2010， 1（3）： 320-331.

[3]P Samadi， R Schober， V W S Wong. Optimal energy consumption scheduling using mechanism design for the future smart grid[C] // IEEE International Conference on Smart Grid Communications （SmartGridComm）， 2011： 369-374.

[4]S R Bu， F R Yu， P X Liu. A game-theoretical decision-making scheme for electricity retailers in the smart grid with demand-side management[J]. In： 2011 IEEE international conference on smart grid communications （SmartGridComm）， 2011， 387-391.

[5]代业明，高岩.基于智能电网需求侧管理的多零售商实时定价策略[J].中国电机工程学报，2014，34（25）：4244-4249.

[6]F L Meng， X J Zeng. A stackelberg game-theoretic approach to optimal real-time pricing for the smart-grid[J]. Methodologies and application， 2013， 17（12）： 2365-2380.

[7]C Chen， S Kishore， L Snyder. An innovative rtp-based residential power scheduling scheme for smart grids[J]. In： Acoustics， speech and signal processing （ICASSP）， 2011 IEEE international conference on IEEE， 2011， 5956-5959.

[8]A H Mohsenian-Rad， A Leon-Garcia. Optimal residential load control with price prediction in real-time electricity pricing environments[J]. IEEE Transactions on SmartGrid， 2010，1（2）： 120-133.

[9]W Saad， Z Han， H Poor， et al. Game-theoretic methods for the smart grid： An overview of microgrid system demand-side management， and smart grid communications[C]//IEEE Signal Processing Magazine， 2012， 29（5）： 86-105.

[10]代业明，高岩.具有多类资源多类用户智能电网实时定价决策[J].系统工程理论与实践，2015（09）：2315-2323.

[11]代业明，高岩.分布式发电系统动态定价决策[J].系统工程，2016（02）：70-75.