关于滑动摩擦力做功的一点想法

2016-11-14北京

高中数理化 2016年19期

◇　北京　俞　鹏　彭　征

(作者单位

关于滑动摩擦力做功的一点想法

◇北京俞鹏1彭征2

在人教版高中物理教材《必修2》第7章第2节“功”当中,其实已对2种功的定义都给出了“明确”的说法:“到了19世纪20年代,法国科学家科里奥利扩展了这一基本思想,明确地把作用于物体上的力和受力点沿力方向的位移的乘积叫作‘力的功’”;“……一个物体受到力的作用,并在力的方向上发生了一段位移,这个力就对物体做了功”．

考虑到给普通高中学生不宜过分强调2种功的区别,教材中对这2种功的区别做了模糊处理．但这种处理方式对那些爱刨根问底的学生而言,可能会引起概念上的混乱．

首先,对这2种功的定义及其使用情景做个明确的说明:对于某一段功ΔW=F·Δs, 位移Δs是谁的?

情况1Δs是作用点的位移,这时对应的功叫作广义功．广义功标志了能量在物体间的转移,即能量转化的量度,但不一定能拿来处理物体的质心动能变化.

情况2Δs是物体(质心)的位移,这时对应的功叫作狭义功,又叫赝功．狭义功不一定能作为能量转化的量度,但可以用在质心动能定理当中来计算质心动能的变化．

如果受力对象的各个细微部分(小到每一个分子)的运动轨迹都完全一样(绝对的平动),那么作用点的位移自然就是物体质心的位移,此时广义功和狭义功是一样的,因此这种情况下我们写出的功既可以用来计算功能关系,也可以应用到动能定理．比如:用绳将一个重力为mg的木块缓慢提高h,绳对木块做的功W=mgh可以同时表示2种功(广义功和狭义功)．因此,一方面W可以表示绳传递给木块的能量，另一方面W也可以用在对木块的动能定理当中，即W-mgh=0-0．

但是,对于作用点和质心位移不一样的情况,使用这2种功就应当注意区别了．

在举例之前,先对质点组的能量情况做个说明:

对于一个由N个质点构成的系统,Fi表示第i个质点受到的所有外力,Fij表示第i个质点对第j个质点的内力,则对第i个质点列出方程:

方程两边同时对i求和,可得:

①

式①常被人叫作质点组的动能定理,即系统所有质点的总动能变化量等于外力对每个质点做的功与所有内力做功之和,如果认为每个质点都不具有从式子中涉及的力获得“内部能量”的能力(比如原子能级的跃迁),则这里的功都可以当作广义功,即都可以用来描述能量的转移．事实上,上式左边第1项代表了外界与系统的能量交换,第2项则代表了系统内部势能与动能的转化．

对该质点组的能量,还可以有另外一种处理方式:

②

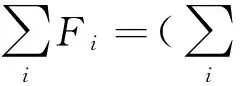
图1

分析该问题一般这样处理:将做功考虑成力乘以受力物体的位移,则摩擦力对小木块做功为W1=-Ffs1,摩擦力对长板做功为W2=Ffs2,可以看出这里求得的应当是狭义功,因此可以利用W1和W2对木块和木板分别使用动能定理,易得小木块动能减少了Ffs1,长板动能增加了Ffs2,而一对摩擦力做的总功就是W1+W2=-FfL,这就是耗散产生的热量．

然而,对于上面的这种解释,总是有一些爱钻研的同学会提出这样的问题:木板对小木块做了-Ffs1的功,木板将从木块那里得到Ffs1的能量，而木块对木板做了Ffs2的功,木块将给木板Ffs2的能量，那么事实上木块到底给了木板多少能量呢?

这个问题里涉及滑动摩擦力,其实滑动摩擦力的成因非常复杂,我们并不十分清楚,但可以认为滑动摩擦力应该是接触面上若干个分子之间相互作用的结果,所以滑动摩擦力Ff应该是若干个分子间作用力Ffi的合力,即Ff=∑Ffi．实际上,我们不可能去研究出每个分子在相互作用时的位移si,因此我们在计算摩擦力做功时就只有一个选择了:直接用∑Ffi乘以质心的位移sc．因此,笔者认为:滑动摩擦力做功为狭义功,不可以拿来讨论功能关系!由此可知,上面的W1和W2都是赝功,都不能描述木块给了木板多少能量,只能描述木块和木板的(质心)动能变化．至于生热Q=Ffs相对=FfL是能量转化的结果,它在任何参考系里看也不可能是广义功,因此Ffs相对也不能拿来描述功能关系,只能用来表示耗散的机械能．

同样,还是在人教版高中物理教材《必修2》第7章第2节“功”当中,还说了这样一段话:“当一个物体在几个力的共同作用下发生一段位移时,这几个力对物体所做的总功,等于各个力分别对物体所做功的代数和．可以证明,它也就是这几个力的合力对物体所做的功．” 然而,应当注意的是,这段话只是对狭义功才是正确的,因为在计算狭义功时,可以有

②

若是对于广义功,系统各质点的位移可能不同,则合力该乘以谁的位移呢?就算乘质心,也是

②

因此,教材中的这段话对于广义功是不对的,所以,教材这样处理其实有点引导学生们走狭义功和动能定理这条路的意思．不过这样做也很有道理,毕竟,滑动摩擦力做功的问题是回避不了的,而按前文中的观点,滑动摩擦力做功都只能是狭义功．

广义功和狭义功这2种功的形式我们都应该关注并且了解,广义功拿来算功能关系,狭义功用来解决质心动能,各有意义,没有优劣之分,我们不能完全回避某一种功,也不能将这2种功混淆使用．其实,有很多能量问题如果能从广义功和狭义功2个方面都做分析,往往可以理解得更加透彻．

分析假设汽车的截面积为A,当汽车以一定速度运动时,将推动前方的空气使之获得相应的速度,则在Δt时间内,车前方以A为底、vΔt为高的柱形空气获得的动能ΔEk=Δmv2/2=ρAvΔt×v2/2.