引例说明数列问题求解方略

◇　山东　王　慧

(作者单位：山东省枣庄市枣庄八中南校)



引例说明数列问题求解方略

◇山东王慧

数列是高中数学主干内容之一,其中与数列的前n项和、递推关系有关的内容是高考重要考查点.问题处理的关键是通过构造、转化,将一般数列化归为特殊数列求解．下面引例说明．

(1) 求a1的值;

(2) 求证:(n-2)an+1=(n-1)an-1(n≥2);

(3) 判断数列{an}是否为等差数列,并说明理由.

本题以等差数列为背景,给出其前n项和公式,证明其递推关系,并判断{an}为等差数列．

第(1)问属于基础题,下面对第(2)、(3)问的解答进行探究．

1　常规解答

与通项公式有关的内容主要有: 1) 给出前n项和求通项公式．求解方法通常是利用公式an=Sn-Sn-1(n≥2)． 2) 给出递推关系求通项公式．此类问题的求解方法较多,但本质是“构造”,即根据已知递推关系将其构造为特殊的等差或等比数列,再利用等差或等比数列的通项公式求解．

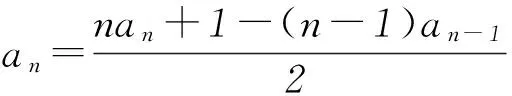
(3) 方法1数列{an}是等差数列.理由如下:

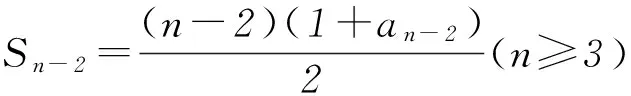
因为n≥3, 所以an-2an-1+an-2=0,即an-an-1=an-1-an-2(n≥3). 所以数列{an}是以1为首项、a2-1为公差的等差数列.

2　思路拓展

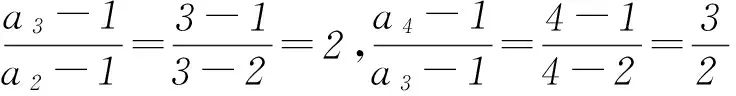
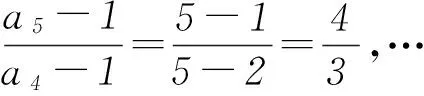
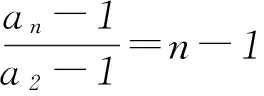
方法4若数列{an}为等差数列,则有an=a1+(n-1)d,下面用数学归纳法证明:

当n=1时,等式成立; 设当n=k(k≥2)时,等式成立,即ak=1+(k-1)d．

当n=k+1时,

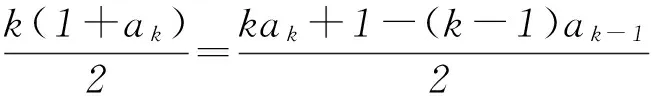
(k-1)ak+1+1=kak.

又因为ak=1+(k-1)d,所以

(k-1)ak+1+1=k[1+(k-1)d],

即ak+1=1+kd,所以数列{an}是以1为首项、d为公差的等差数列.

3　变式探究

证明必要性：设数列{an}的公差为d．

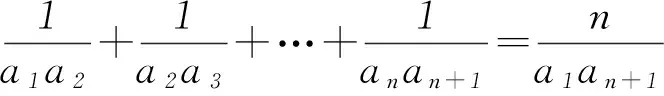
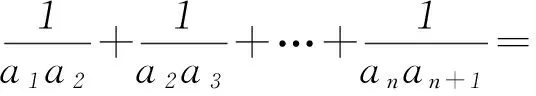
充分性：数学归纳法证明.

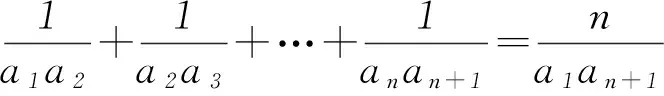
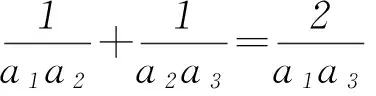
设ak=a1+(k-1)d．由已知等式可得

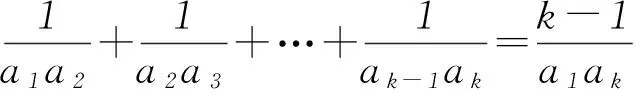
①

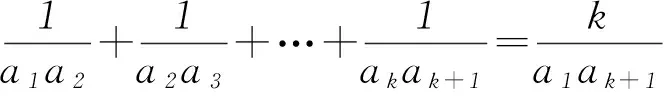
②

将式①代入式②得

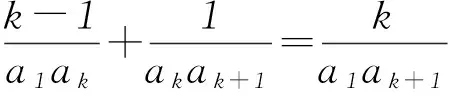
在此式两端同乘以a1akak+1,得

(k-1)ak+1+a1=kak.

③

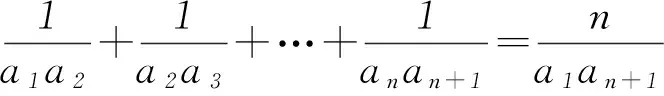
(作者单位：山东省枣庄市枣庄八中南校)