潮滩上应用ADV进行波浪观测与特征参数计算

芦军，范代读，2，涂俊彪，张悦，张艳伟

（1.同济大学海洋地质国家重点实验室，上海　200092；2.长江大学地球科学学院，湖北　武汉　430100）

潮滩上应用ADV进行波浪观测与特征参数计算

芦军1，范代读1，2，涂俊彪1，张悦1，张艳伟1

（1.同济大学海洋地质国家重点实验室，上海200092；2.长江大学地球科学学院，湖北武汉430100）

声学多普勒流速仪（ADV：Acoustic Doppler Velocimetry）可以同时测量水体流速与水压的高频变化信息，通过合理的设置采样工作模式和数据后处理方法，可以计算得到高精度的波浪特征参数。本次实验选择在长江口南汇边滩低潮滩开展野外观测，布放仪器包括ADV和光学后向散射浊度计（OBS）各一台，均采用连续工作模式，ADV采样频率为32 Hz。数据处理首先进行原始流速观测数据的信号质量检查和异常值去除等步骤，剔除信噪比小于5 dB或相关系数小于70%的观测数据；对压力数据进行中心化和消除趋势项处理，降低因潮位变化引起的偏移。在运用传递函数将压力谱转换成表面波谱时，需要首先确定一个截断频率，对比分析发现，潮滩环境采用高频截断频率固定在0.5 Hz效果最理想。通过计算得到观测期间的主要波浪特征参数值分别为，有效波高为0.03～0.51 m，平均有效波高为0.3 m；平均周期为2.52～7.22 s，平均跨零周期为2.46～6.57 s；波浪的轨道流速为0.03～0.13 m/s，平均轨道流速为0.09 m/s。波高与水深之间具有良好的正相关关系，说明对于潮滩上固定站点，涨落潮水位变化是制约波高发展的重要因素。可见，ADV可以实现对潮滩流场和波浪作用的同步观测，为开展波流共同作用下潮滩沉积地貌演变的沉积动力学研究提供了手段与方法支持。

潮滩；ADV；异常值处理；截断频率；波浪参数

波浪和潮流是河口海岸地区重要的动力因素。和周期性的潮流相比，短周期的波浪更加复杂和难于观测，但其对河口海岸地区沉积物的再悬浮与输运有着重要影响。Sanford（1994）在对切萨匹克湾泥质底床冲淤变化的研究发现，波浪导致沉积物再悬浮是潮流作用的3～5倍。Christie等（1999）通过对亨伯河口湾研究，发现风暴天气条件下潮滩悬沙浓度要比平静天气大一倍多。Ralston等（2007）在对旧金山湾潮间带研究发现，当风浪趋于平静时水体中悬沙浓度迅速下降。开敞型潮滩更易受波浪的影响，波流相互作用是塑造沉积地貌的重要机制（Fan，2012）。江浙沿岸潮滩现场观测表明，风浪的出现和加强导致水体悬沙浓度显著增加与滩面发生蚀低等现象（李平等，2008；Wang et al，2012；Zhu et al，2014）；涨落潮水位和流速变化影响风浪过程与再悬浮沉积物输运距离与通量，从而形成不同的潮滩蚀淤剖面（Fan et al，2006）。可见，开展潮滩波浪的现场观测与研究具有重要意义。

在传统波浪观测方法中，压力测波法是一种比较常用的方法，传统的压力测波法是利用在海底固定压力测波仪，通过仪器中高分辨率的压力传感器感应波面升降所引起的压力变化，从而记录波面的起伏变化（Cavaleri，1980；刘华兴，2010），比如美国InterOcean公司生产的S4ADW压力式波浪仪和中科院南海所研发的SAS3-1型压力式波潮仪（龙小敏等，2005）。声学多普勒流速仪（ADV：Acoustic Doppler velocimetry）是一种利用多普勒原理测量流速的仪器，能够同时高精度且高分辨率地测量水体中的流速与水压变动信息，后者为利用ADV反演波浪信息提供了可能。最早由Gordon等（1999，2001）分别在破浪带和浅水区域测试并对比了ADV和Aquadopp测量波浪的准确度，认为这两种仪器都能够准确地观测波浪的波谱和波高。运用Gordon方法，Bolanos等（2010）将迪河河口观测获得的ADV压力数据转换成波高；MacVean等（2014）把在旧金山湾内泥质潮滩观测的ADV数据，通过计算获得了波浪的波高、周期以及轨道流速等参数。国内就目前所知，尚未见利用ADV进行波浪特征参数反演的相关报道。本文在结合前人关于压力测波法研究的基础上，利用长江口南汇边滩的一组ADV观测数据进行波浪参数的反演计算，探讨该方法的实用性和有效性。

1　研究区域和方法

1.1研究区域

南汇边滩地处长江口和杭州湾的交汇地带（图1），外形呈犁头状，是长江口近岸泥沙输运及其与杭州湾交换的通道，受长江丰富的泥沙供应以及杭州湾北部潮流的影响，在两者结合部形成了宽广的边滩。南汇边滩受波浪、潮汐和径流的共同控制，其中潮汐属于非正规浅海半日潮，年平均潮差3.2 m，大潮潮差可达4 m以上，河口口门附近年均波高为1 m，最大波高可达6.2 m（上海市海岛资源综合调查报告编写组，1996）。

1.2野外仪器布放与工作模式

为了进行仪器的方法性实验和小尺度波流相互作用过程观测，分别于2013年9月5-7日在南汇边滩的低潮滩上设立观测站S1（30°59′8.59″N，121°57′14.15″E，图1），2013年9月9-10日设立观测站S2（30°52′17.44″N，121°56′49.67″E），均放置ADV和OBS（Optical Back Scatter）各一台。ADV为Nortek公司生产的6 MHZ声学多普勒流速仪，测量精度为测量值的0.5%或者±0.1 cm/s，观测期间探头上视，其中S1站位流速探头距底床高度为0.52 m，压力传感器距底床高度为0.68 m。OBS为Campbell公司生产的光学后向散射浊度计，探头距底0.52 m（图1）。为了得到悬沙浓度值，在S2站位观测期间每隔15 min取OBS探头同层位水样约500 mL，共计22个样品；带回室内进行静置、去掉上层清液、烘干和称重等，求得悬沙浓度；进行OBS浊度值与悬沙浓度的相关性分析，相关系数达0.62（未发表数据）。S1站点未进行同步取水样实验，OBS悬沙浓度换算采用S2站点的拟合关系式。

图1　长江口南汇边滩野外观测站点位置（a）和仪器布放方式（b）

在野外仪器布放进行采样之前需制定详细的工作模式，包括采样频率、时长以及间隔等（Schwartz，2006）。采样频率和时长的选择需要根据测点的波浪特征，因此在观测实验之前需尽量收集研究区已有的波浪资料进行分析，了解历史上波浪的最高频率，进而根据奈奎斯特采样定理确定采样频率。采样时长的选择取决于测点波浪的峰值周期，一般来说，采样时长至少是后者的150倍（Schwartz，2006）。采样间隔的选择取决于观测目的，本文主要目的是仪器的方法性实验和小尺度波流相互作用过程观测，在存储和续电能力许可下采用了连续工作模式，ADV采样频率为32 Hz，OBS采样间隔为10 s。

1.3波浪参数计算方法

海面以下某深度的水压可分为两部分，一是平均海平面到此深度所产生的压力，称为静压，另一是波动所产生的压力，称为动压（文圣常，1984）。根据线性波理论，水面下Z处动压随时间变化为（式1）：

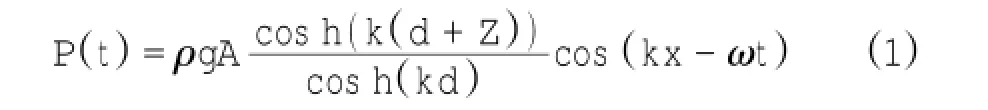
式中，ρ为海水密度，g为当地重力加速度，A为表面波振幅，d为水深，k为波数（k=2π/L，L为波长），ω为波浪圆频率（ω=2π/f，f为波浪频率）。根据表面波弥散关系，波数和频率关系如下：ω2=gktan h（kd）。因此，在获得高频压力数据后，需先将压力数据转化为压力谱，再根据线性波理论，将压力谱转化成表面波谱（式2）：

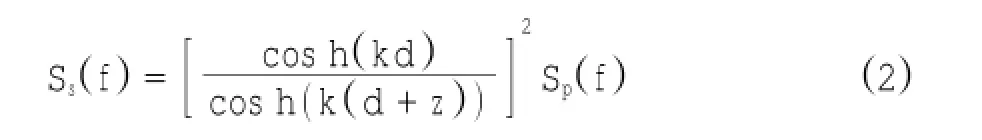
式中，Ss（f）为表面波谱，Sp（f）为压力谱，z为传感器所在深度 （z轴向上为正） （Gordon et al，2001）。

一般将一段时间内观察到的波高按从大到小排列，其中三分之一最大波高的平均值即为有效波高（Longuet-Higgins，1952；Dalrymple et al，1991）。对于谱分析，我们用谱矩来描述谱的分布，n阶谱矩定义如下：

假设表面波高遵循瑞利分布，则有效波高等于（徐德伦，2001），其中为表面波谱的零阶谱矩，即：

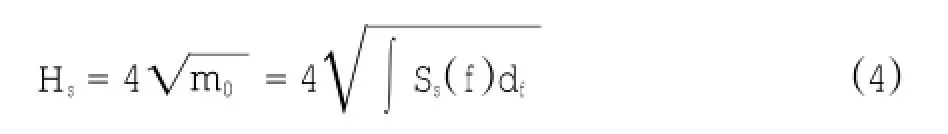
计算出有效波高后，还可计算其他特征波高参数，如均方根波高，十分之一波高H1/10=1.8 Hrms=1.27 Hs。

和利用表面波谱计算波高一样，也可以通过表面波谱来计算波浪的周期参数。通过表面波谱计算的平均跨零周期为（Earle，1996），其中m2为表面波谱的二阶谱矩，平均周期则可以通过Tm=m0/m1（Wiberg et al，2008）计算得到，式中m1为波谱的一阶谱矩。对于波浪的研究而言，波浪的谱峰周期Tp也是一个重要的特征量，它被定义为波浪谱中最大谱值所对应的周期，可通过计算波谱中最大值所对应的频率，再求其倒数获得Tp值。本文只讨论波浪的有效波高、平均跨零周期和平均周期等常用的参数。

在波浪的研究中，波浪的轨道运动导致底质沉积物的再悬浮，因此波浪的轨道流速也是一个十分重要的参数。和波高、周期的计算一样，对ADV测量的高频流速数据进行处理可以得到波浪的轨道流速（Wiberg et al，2008；MacVean et al，2014），即：

式中，Suv=Suu+Svv，Suu、Svv为ADV测量的水平流速谱。

2　结果与讨论

2.1观测期间水文特征

观测期间（2013年9月5日下午至7日上午）共经历3次涨落潮周期（图2），主要盛行偏北风，风速变化范围为2～6 m/s，平均风速4.36 m/s（浦东国际机场气象站资料）。结果表明，南汇边滩潮汐不对称性较明显，落潮历时比涨潮历时长约1 h，涨潮流速最大值和平均值均大于落潮流速对应值。3个潮周期的涨潮平均流速0.32 m/s，落潮平均流速0.28 m/s，前者约为后者的1.14倍，全潮平均流速为0.31 m/s。涨潮流向平均值为307°，落潮流向平均值为129°，呈现明显的往复流性质。

观测期间最大含沙量为2.3 kg/m3，各潮周期平均含沙量1.5 kg/m3，涨潮平均含沙量为1.8 kg/m3，落潮平均含沙量为1.3 kg/m3，涨潮含沙量大于落潮含沙量。潮周期内含沙量变化曲线呈现“U”型，谷值对应于转流阶段的流速低值区，峰值通常出现在涨潮初期和落潮末期，反映了波浪和潮流共同作用下潮滩沉积物再悬浮的特征，这种作用在浅水条件下表现更为显著，形成悬沙浓度峰值。

2.2ADV流速观测异常值的处理

与传统流速测量设备相比，ADV具有采样体积小，采样频率高和非接触的特点（Nortek，2005），但是同所有仪器一样，ADV也容易受到外界环境的干扰。水体气泡、大颗粒悬浮物以及边界回声强度和脉动强度等因素都会影响ADV测量的相关系数，进而导致测量的信噪比下降（Fugate et al，2002）。当实际流速超出了ADV流速的预设值，将会导致测量值失真，出现明显的异常值或毛刺点（Goring et al，2002；鲁远征等，2012）。海岸带复杂的水动力环境也会使ADV的测量受到影响（Trowbridge et al，2001）。因此，对原始观测数据进行（1）信号质量的检查和（2）去除异常值，成为ADV数据分析研究的首要步骤。

一般认为，ADV测量数据信噪比（SNR）小于5 dB或相关系数小于70%时，数据质量较差应予以舍弃（Chanson et al，2008）。Goring等（2002）认为ADV所测量的数据集中在一个三维空间的椭球体内，若测量的数据超出椭球体在各个平面上的投影，则认为测量数据的精度较低，为此提出相空间阈值法进行去噪分析。虽然本次观测原始数据的异常值并不多（图3a方框所示部分），只有一些值超出了实际流速的范围，个别甚至超过仪器设定的量程（4 m/s），但他们仍会对后续的计算造成较大的误差。采用Goring等（2002）的相空间阈值法进行异常值剔除（或称去毛刺，despiking）处理，得到一组比较规整的数据（图3b）。

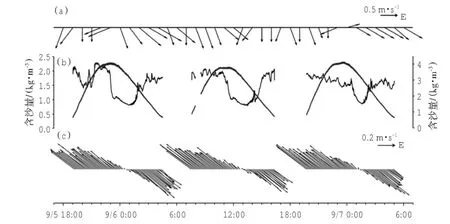
图2　观测期间风场（a）、水位（灰色）与悬沙浓度（黑色，b）及流速（c）变化特征

图3　ADV实测原始流速数据（a）与剔除异常值后真实流速数据（b）对比，（a）中灰色区域内为异常值

为了便于进行谱分析和后续计算，将连续观测数据重新分组，从整点时刻开始每隔10 min取前512 s观测数据，首先进行信号质量检查，然后进行异常值的去除。观测原始数据显示，在仪器刚入水或者即将出水一段时间内，SNR<5 dB或者相关系数小于70%的数据占有一定的比例，而在仪器持续没入水面一段时间后，基本上不存在相关系数小于70%或者SNR<5 dB的情况（图4）。同样，ADV实测流速数据的异常值分析表明，在仪器刚入水或者即将出水一段时间内容易出现异常值，其他时间段异常值较少见（图5）。这些未通过信号质量检查的时段或是判断为异常值的数据，都需要在后续波浪特征参数计算之前予以舍弃或进行异常值剔除处理。

2.3波浪信号中潮位变化项的剔除

尽管将ADV连续观测数据分成了512 s一组，时间较短，但是潮汐变化对测点的水面高度仍然产生了不可忽视的影响，尤其是涨、落急阶段。因此在利用高频水深数据进行波浪特征参数计算之前，必须对原始数据进行中心化以及消除趋势项处理（陈子燊等，2001；李志强等，2010）。中心化就是将数据减去其均值，使原始序列转变成零均值序列。而在进行功率谱的处理时，趋势项的存在会使谱出现变形，甚至可能使低频时的谱估计失真（高品贤，1994），因此在水压信号的处理中必须要消除趋势项。本文采用多项式最小二乘法消除趋势项（李东文等，2008）。

2.4ADV压力谱转换成表面波谱时截断频率的选择

由于水层对波浪信号的衰减作用，频率越高衰减作用越强烈。图6（a）展示了一个从压力观测数据获得的特征压力谱（9月7日0点到0:10的观测数据），从图中可以看出当波浪频率大于0.4 Hz时，波浪信号几乎衰减为0。因此，在处理高频压力数据时，需要将压力谱通过传递函数：

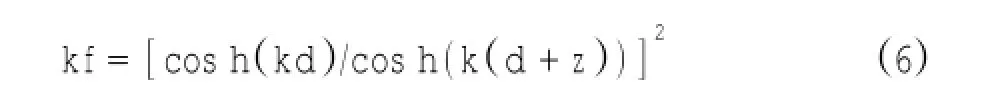
图4　观测期间ADV实测流速数据出现信噪比小于5 dB（a）和相关系数小于70%（b）的个数统计

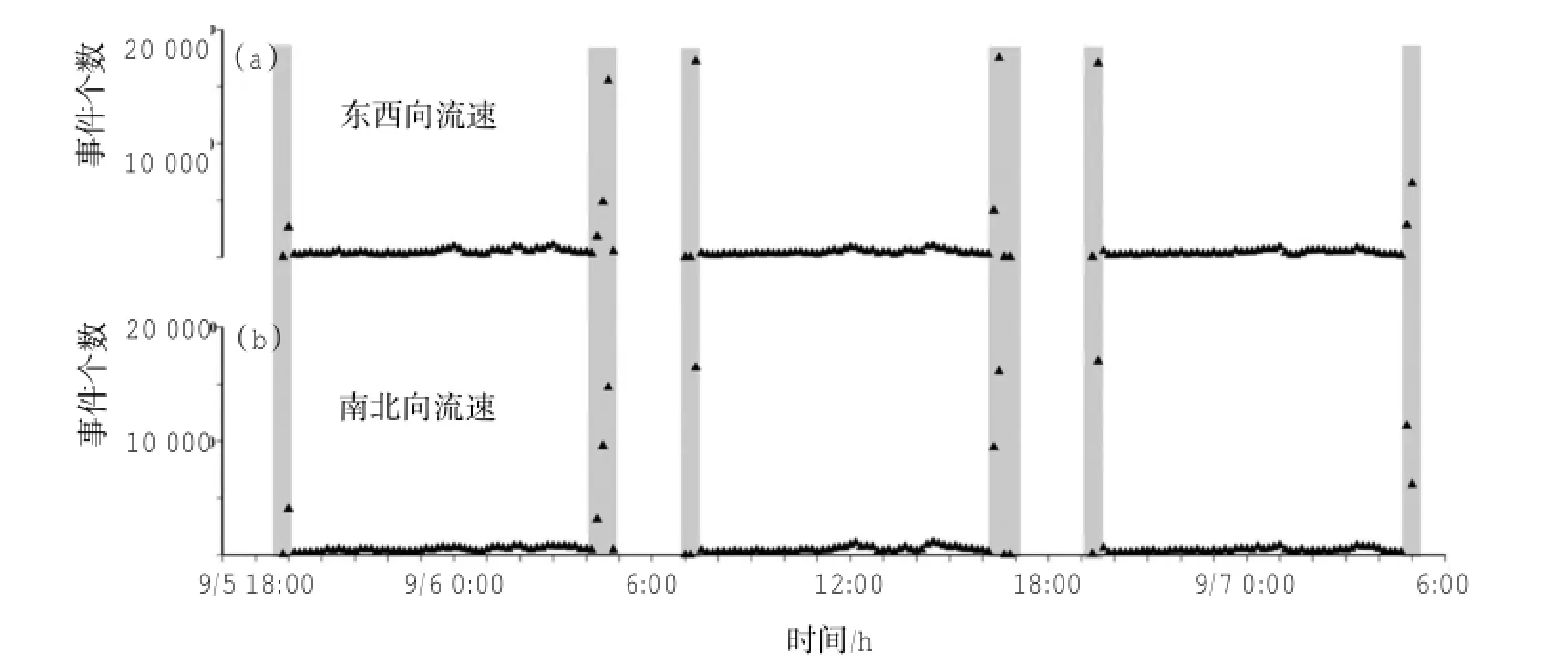
图5　观测期间ADV实测流速中出现异常值次数统计：（a）东西向流速分量，（b）南北向流速分量

转换成表面波谱（见公式2）。图6（b）即是通过转换获得的表面波谱，由此可见，虽然可以通过传递函数补偿水层对波浪信号的衰减作用，但也使所得表面波谱在高频部分迅速增加，在1 Hz时功率谱密度竟达到了1.3×107m2·s，这与实际情况并不相符，因此在计算时需要确定一个截断频率。

图7显示了压力传感器固定在距底0.5 m，水深在1、2、3、4、5 m时传递函数随频率变化的情况。可见，当水深一定时，传递函数会随着频率增高而逐渐变大，导致仪器噪声和信号一起增大。与高频波浪信号相比，当仪器噪声增大到不可忽略时，会使表面波谱的高频段产生很大误差。随着水深的增加，水层对高频信号的衰减更加强烈，同频率下传递函数也越来越大，因此选取合适的高频截断频率便成了准确计算波高和周期的关键前提。目前利用压力测波法观测波浪时，对高频截断频率的选择有4种方法（图7）：（1）Gordon等（2001）在近岸浅水区利用ADV测量波浪时，令传递函数等于定值 200，即 kf=200； （2） Wiberg等（2008）认为利用波谱计算波浪参数时，截断频率选择与测点水深有关，即：

d为水深；（3）陈子燊等（2002）在海滩破波带利用压力测波法时，认为截断频率与仪器在水中深度有关：

hp为仪器所在深度；（4）MacVean等（2014）在泥质潮滩利用ADV观测波浪时，将截断频率固定在特定频率，即fmax=0.5。

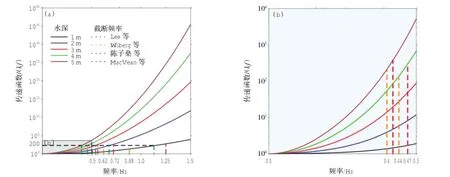
图7　不同水深情况下传递函数随频率变化

对比发现，如采用Gordon方法，1 m水深的截断频率为1.15 Hz；但在实际计算中，发现在此频率下仪器噪声和衰减的高频信号已经变的不可区分，求得的表面波谱在高频部分发生了严重的畸变，所得数值巨大，如图6（b）所示，因此认为该方法在此并不适用。对于陈子燊的方法，仪器固定在距底0.5 m处，1 m水深时的截断频率为1.25 Hz，在后续计算中出现与Gordon方法相似的问题，故予以舍弃。如运用Wiberg方法，则存在对于水深较大的情况截断频率偏低，使原本有用的高频信号丢失，则造成计算所得的波高、周期的偏低，因此也不适用于本次实验。MacVean在泥质潮滩观测中将截断频率固定在0.5 Hz，并没有上述方法造成的高频信号失真和高频截断频率偏低的问题，而且通过计算发现，结果能够很好地反应当时的波浪情况，因此在高频截断频率的选择上本文采用MacVean等提出的方法。对于低频截断频率，由于一般研究的波浪周期在30 s以下，因此将低频截断频率定在0.03 Hz，所以本文通过表面波谱计算波高、周期和轨道流速的频率定在0.03～0.5 Hz，图6（c）显示了将截断频率定在0.03～0.5 Hz的特征表面波谱。

2.5波浪特征参数

波浪参数计算结果表明（图8），观测期间3个潮周期内波浪的平均周期（Tm）为2.52～7.22 s，均值为4.72 s，平均跨零周期（Tz）为2.46～6.57 s，均值为4.28 s，波浪的平均跨零周期要小于平均周期，但两者的变化趋势相同。波浪轨道流速是波浪对潮滩底床产生底切应力的基本因素，进而导致底部沉积物的起动与再悬浮，观测期间波浪轨道流速为0.03～0.13 m/s，平均轨道流速为0.09 m/s。

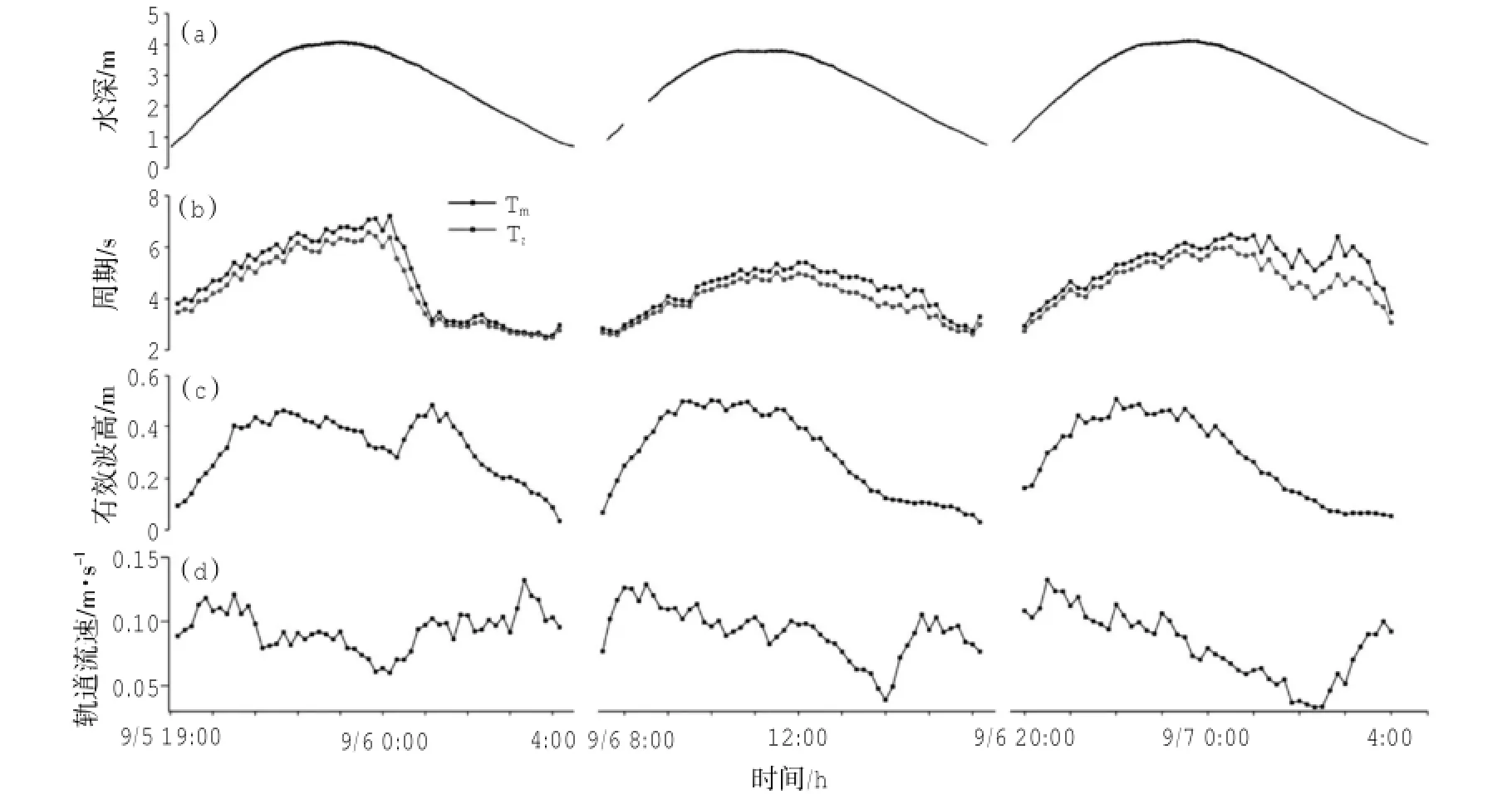
图8　观测期间水位（a）、平均波浪周期和平均跨零周期（Tm，Tz，b）、有效波高（c）和轨道流速（d）随时间变化序列

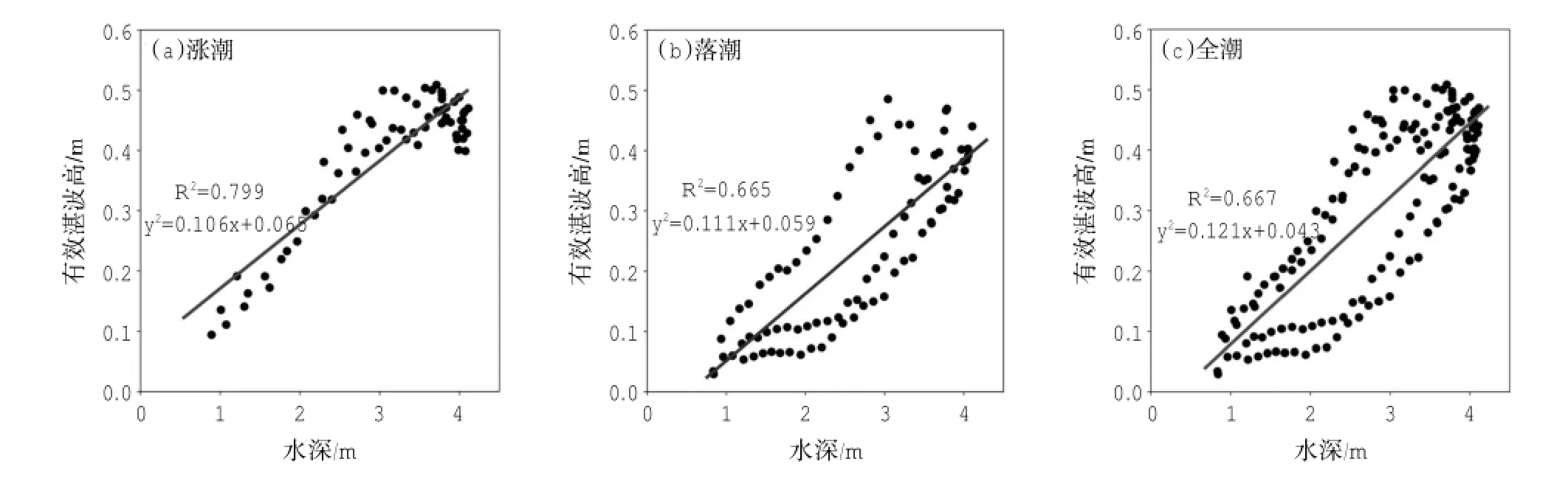
图9　有效波高与水深相关性：（a）涨潮，（b）落潮，（c）全潮

相对波高（波高与水深之比）是衡量波浪与底床作用的重要参数，也是判断波浪是否破碎的重要指标。一般认为相对波高为0.8～1.2 m时波浪则发生破碎（Woodroffe，2002），而在波高或水深一定时，相对波高越大，波浪与底床的作用越强烈。观测期间，相对有效波高为0.03～0.17 m，均值为0.10 m。Hir等（2000）在法国Brouage的障壁型潮滩上测得的相对波高通常小于0.15 m，而陈燕萍等（2012）在开敞型潮滩崇明东滩测得的相对波高一般大于0.16 m，有些甚至大于0.2 m。南汇边滩开敞程度不同，南侧直接面向开阔海，而东侧潮滩受波浪影响程度随着与南槽口门距离的增加而降低，本次观测站点位于口门以内一段距离（图1），因此相对波高更接近于障壁型潮滩。0.03～0.51 m，平均有效波高为0.3 m；平均周期为2.52～7.22 s，平均跨零周期为2.46～6.57 s；波浪的轨道流速为0.03～0.13 m/s，平均轨道流速为0.09 m/s。波浪的波高和水深之间呈很好的正相关关系，对于某一固定的观测点来说，波高随着涨潮水深加大而增加，随着落潮水深减小而下降，涨潮期间相关系数要大于落潮期间相关系数，可见水深是制约波高发展的重要因素。总之，声学多普勒流速仪（ADV）可以实现近岸波浪的观测，为进一步研究波流联合作用下潮滩水动力和沉积动力特征提供了条件。

3　结论

利用声学多普勒流速仪可以进行波浪观测，观测前需要对采样区域的波浪情况进行调查，以便确定采样频率，采样长度和采样间隔。采样频率和采样长度的选择主要取决于观测点的波浪特征，而采样间隔则取决于研究的目的。由于ADV观测容易受到外界环境的干扰，因此需对ADV流速数据进行信号质量检查和异常值去除处理，而压力数据则需要进行中心化和消除趋势项处理。通过对比研究认为，表面波谱计算的截断频率选择在0.03～0.5Hz。

分析结果显示，观测期间南汇潮滩存在明显的潮汐不对称性，涨潮历时小于落潮历时，涨潮平均流速为0.32 m/s，落潮平均流速为0.28 m/s。观测期间最大含沙量为2.3 kg/m3，平均含沙量为1.5 kg/m3，涨潮含沙量大于落潮含沙量。波浪的有效波高为

Bolaños R,Souza A,2010.Measuring hydrodynamics and sediment transport processes in the Dee Estuary.Earth System Science Data,2: 157-165.

Cavaleri L,1980.Wave measurement using pressure transducer.O-ceanologica Acta,3:339-346.

Chanson H,Trevethan M,Aoki S,2008.Acoustic Doppler velocimetry (ADV)in small estuary:field experience and signal post-processing.Flow Measurement and Instrumentation,19:307-313.

Christie M C,Dyer K R,Turner P,1999.Sediment flux and bed level measurements from a macro tidal mudflat.Estuarine,Coastal and Shelf Science,49:667-688.

Dalrymple R A,Dean R G,1991.Water wave mechanics for engineers and scientists.Prentice Hall.

Earle M D,1996.Nondirectional and directional wave data analysis procedures.NDBC Tech.Doc,96-01.

Fan D D,2012.Open Coast Tidal Flats.In:Davis R A Jr and Dalrymple R W(eds.),Principles of Tidal Sedimentology,New York:Springer, 187-229.

Fan D D,Guo Y X,Wang P,et al,2006.Cross shore variations in morphodynamic processes of an open-coast mudflat in the Changjiang Delta:with an emphasis on storm impacts.Continental Shelf Research,26:517-538.

Fugate D C,Friedrichs C T,2002.Determining concentration and fall velocity of estuarine particle populations using ADV,OBS and LISST. Continental Shelf Research,22:1867-1886.

Gordon L,Clarke L,1999.Aquadopp and Vector wave measurement near Scripps Pier.Nortek Technical Note No:011.

Gordon L,Lohrmann A,2001.Near-shore Doppler current meter wave spectra.Proceedings of the 4th International Symposium on Ocean Wave Measurement and Analysis,WAVES2001,ASCE,San Francisco,CA,33-43.

Goring D G,Nikora V I,2002.Despiking acoustic Doppler velocimeterdata.Journal of Hydraulic Engineering,128:117-126.

Le Hir P,Roberts W,Cazaillet O,et al,2000.Characterization of intertidal flat hydrodynamics.Continental Shelf Research,20:1433-1459.

Longuet Higgins M S,1952.On the statistical distributions of sea waves. Journal Marine Research,11(3):245-265.

MacVean L J,Lacy J R,2014.Interactions between waves,sediment,and turbulence on a shallow estuarine mudflat.Journal of Geophysical Research:Oceans,119:1534-1553.

NORTEK,2005.Vector Current meter user manual.Norway:Nortek AS, Vangkroken 2.

Ralston D K,Stacey M T,2007.Tidal and meteorological forcing of sediment transport in tributary mudflat channels.Continental Shelf Research,27:1510-1527.

Sanford L P,1994.Wave-forced resuspension of upper Chesapeake Bay muds.Estuaries,17:148-165.

Schwartz M L,2006.Encyclopedia of Coastal Science.Springer Science& Business Media.

Trowbridge J,Elgar S,2001.Turbulence measurements in the surf zone. Journal of Physical Oceanography,31:2403-2417.

Wang Y P,Gao S,Jia J J,et al,2012.Sediment transport over an accretional intertidal flat with influences of reclamation,Jiangsu coast, China.Marine Geology,291:147-161.

Wiberg P L,Sherwood C R,2008.Calculating wave-generated bottom orbital velocities from surface-wave parameters.Computers&Geosciences,34:1243-1262.

Woodroffe C D,2002.Coasts:Form,Process and Evolution.Cambridge University Press.

Zhu Q,Yang S L,Ma Y X,2014.Intra-tidal sedimentary processes associated with combined wave-current action on an exposed,erosional mudflat,southeastern Yangtze River Delta,China.Marine Geology, 347:95-106.

陈燕萍，杨世伦，史本伟，等，2012.潮滩上波高的时空变化及其影响因素-以长江三角洲海岸为例.海洋科学进展，30（3）：317-327.

陈子燊，李志强，李志龙，等，2002.海滩破波带波性质的统计对比分析.中山大学学报：自然科学版，41（6）：86-90.

陈子燊，欧素英，戴志军，等，2001.岬间海湾滨面带波浪结构和外观统计特征.海洋通报，20（3）：1-7.

高品贤，1994.趋势项对时域参数识别的影响及消除.振动：测试与诊断，（2）：20-26.

李东文，熊晓燕，李博，2008.振动加速度信号处理探讨.机电工程技术，37（9）：50-52.

李平，陈沈良，谷国传，等，2008.长江口九段沙上沙潮滩沉积物短期时空变化特征.海洋通报，27（6）：60-67.

李志强，陈子燊，李志龙，2010.近岸带波浪传播过程中波性质的统计对比分析.广东海洋大学学报，30（4）：43-47.

刘华兴，2010.被动声学测波新方法的实验研究及应用.中国海洋大学.

龙小敏，王盛安，蔡树群，等，2005.SZS3-1型压力式波潮仪.热带海洋学报，24（3）：81-85.

鲁远征，吴加学，刘欢，2012.河口底边界层湍流观测后处理技术方法分析.海洋学报，34（5）：39-49.

上海市海岛资源综合调查报告编写组，1996.上海市海岸带和海涂资源综合调查报告.上海科学技术出版社.

文圣常，1984.海浪理论与计算原理.科学出版社.

吴天行，华宏星，2014.机械振动.清华大学出版社.

徐德伦，于定勇，2001.随机海浪理论.高等教育出版社.

（本文编辑：袁泽轶）

Application of ADV in the tidal flat to observe wave processes and calculate their characteristic parameters

LU Jun1,FAN Dai-du1,2,TU Jun-biao1,ZHANG Yue1,ZHANG Yan-wei1
（1.State Key Laboratory of MarineGeology,Tongji University,Shanghai 200092,China; 2.School of Geosciences,Yangtze University,Wuhan 430100,China）

ADV(Acoustic Doppler Velocimetry)can simultaneously measure the high frequency change of water velocity and pressure.By setting a reasonable sampling mode and selecting an appropriate post-processing method,the wave characteristic parameters can be precisely calculated from ADV data.Our field experiment was carried out by deploying one ADV and one OBS(Optical Back Scatter)on the lower intertidal flat of Nanhui bank(Yangtze River Delta)with a continuous operation mode,and the ADV sampling frequency was set 32 Hz.The original velocity data of ADV should firstly be examined for the signal quality,and some abnormal values should be eliminated(namely despiking)if the signal noise ratio(SNR)was less than 5 dB or the correlation coefficient was less than 70%.The pressure data should be pretreated by the centralization to eliminate the trend deviation by tides.It is important to select an appropriate cut-off frequency when employing a transfer function to convert pressure spectra into surface wave spectra.Comparison studies showed the best solution was to set the upper limit of cut-off frequency with a fixed value at 0.5 Hz for the study tidal flat.The main wave characteristic parameters during the observations were therefore calculated.The results showed that the significant wave height varied from 0.03 to 0.51 m with an average value of 0.3 m;the mean period and zero-crossing period changedrespectively from 2.52 to 7.22 s and from 2.46 to 6.57 s,and the representative bottom orbital velocity varied from 0.03 to 0.13 m/s with an average of 0.09 m/s.There was a high positive correlation between the wave height and the water depth, denoting that the tidal-level change was an important factor in restricting the development of wave heights for a fixed station on the tidal flat.In brief,ADV can be used to gauge both current and wave processes,providing an important tool to study wave-current interactions and their impact on sedimentary and morphological dynamics of tidal flats.

tidal flat;ADV;abnormal-value elimination(despiking);cut-off frequency;wave parameters

P714.1

A

1001-6932（2016）05-0523-09

10.11840/j.issn.1001-6392.2016.05.006

2015-07-05；

2015-08-18

国家自然科学基金（41276045；41476031）；教育部博士点基金（20130072130003）；海洋地质保障专项课题（GZH201100203）；国家海洋局国际合作项目（GASI-GEOGE-02）。

芦军（1990-），男，硕士研究生，主要从事沉积动力过程方面研究。电子邮箱：junloo@126.com。

范代读，博士，教授。电子邮箱：ddfan@tongji.edu.cn。