湍流边界层中颗粒物扩散的双拉格朗日模拟计算

卓　俊，黄流兴，牛胜利，谢红刚

(西北核技术研究所,西安710024)



湍流边界层中颗粒物扩散的双拉格朗日模拟计算

卓俊，黄流兴，牛胜利，谢红刚

(西北核技术研究所,西安710024)

采用拉格朗日方法模拟计算了湍流边界层中气相粒子和颗粒物的运动。其中，气相粒子在流场中按平均风速输送，用一系列随机位移，模拟湍流对扩散的影响，分析了颗粒物在流场中的受力情况，建立了求解颗粒物扩散轨迹的牛顿运动方程。用该方法模拟平板边界层内颗粒物的扩散行为，给出了颗粒物受力及在边界层内的运动轨迹，并将计算的质量通量与文献中的实测值进行了比较。结果表明：计算值与实测值基本吻合，初步验证了本文方法在模拟颗粒物扩散时的可靠性。

气固两相流；颗粒物；湍流；扩散；双拉格朗日

颗粒流体系统在自然界中普遍存在，与生态环境、工业过程及人们日常生活的各个方面密切相关。颗粒流体系统涉及颗粒物输运以及流场与周围环境的相互作用，准确预测颗粒物扩散是环境工程和工农业生产中的重要课题之一[1-3]。同时，湍流流动是自然界常见的现象，在多数工程问题中流体的流动往往处于湍流状态，湍流流动特征在工程中占有重要的地位，湍流研究一直受到研究者的高度重视。

目前，预测粒子在湍流场中扩散的数值计算方法主要有欧拉-欧拉方法和欧拉-拉格朗日方法两种[4-5]。欧拉-欧拉方法，也称为颗粒相拟流体模型，已广泛应用于稠密颗粒相的气固流动体系中。该模型把颗粒相处理为具有连续介质特性的、与气相相互渗透的拟流体，气相和颗粒相都在欧拉坐标下进行求解，仿照单相流动对颗粒湍流脉动进行模拟，应用颗粒动力学理论及分子运动论使方程组封闭。颗粒相拟流体模型最大的优点是可以全面地考虑颗粒相的输运特性，并进行大规模的工程问题计算。但其中的颗粒连续性假设，削弱了气固两相流中非均匀结构的真实性，计算中无法体现颗粒的大小、密度等物理性质的区别，模拟结果也无法揭示颗粒复杂的变化经历[4]。欧拉-拉格朗日方法将流体相处理为连续相，在欧拉坐标系下，建立维纳-斯托克斯方程组求解连续相的流动、传热及反应特性，而在拉格朗日坐标系下，应用牛顿第二定律跟踪求解流场中的每一个离散粒子的运动轨迹，以反映整个离散颗粒场；连续相-离散相的相互作用服从牛顿第三定律，以源相添加于各自的求解方程中实现相间的作用耦合。在该模型中，如何合理描述气相湍流场对颗粒运动的影响是一个主要难题。虽然参照气相对湍流扩散的拉格朗日描述，引入了颗粒湍流运动的拉格朗日时间尺度概念，但不同尺度颗粒物的拉格朗日时间尺度计算方法及其计算结果的可靠性，都还有待进一步研究。

为克服欧拉-拉格朗日方法在模拟计算中遇到的困难，近年，有学者提出了气相和固相均用拉格朗日方法描述的双拉格朗日方法，用来模拟计算颗粒相在湍流中的扩散过程[6-7]。该方法适用于颗粒浓度很低，可以忽略气相中由颗粒引起的扰流情况，即稀相流情形。根据气固两相系统中气相运动的特点，将两相流动中颗粒的运动过程分解为受冲力支配的瞬时碰撞运动及受流体曳力控制的悬浮运动，从而建立了颗粒运动模型。该模型中，流体和颗粒的运动规律均用拉格朗日方法求解。

本文介绍了双拉格朗日方法的物理模型，建立了基于双拉格朗日方法的气固两相流数值计算模型，用编制的计算机程序，模拟计算了无限平板边界层中固体颗粒的扩散过程，并将计算结果与文献中的实验数据进行了对比，从而对本文方法的正确性进行了初步验证。

1物理模型

双拉格朗日方法中，用大量标记粒子表征气相和固相粒子的扩散，如图1所示。假设在某时刻t，气相粒子和颗粒物在流场中处于相同的位置，即Xg(t)=Xp(t)，记该点为O，并假设此时气相粒子和颗粒物的瞬时速度已知，分别为Vg(t)和Vp(t)，在经过一段时间间隔Δt后，气相粒子和颗粒物分别运动至F点和P点，其坐标分别为

(1)

(2)

在t+Δt时刻，粒子的瞬时速度Vp(t+Δt)可由颗粒运动方程计算得到：

(3)

其中，mp为所跟踪固体颗粒的质量；Fi表示固体颗粒在流场中所受的作用力。在计算固体颗粒在P点附近的受力大小时，需要预先知道同在P点处的气相瞬时速度VP,g(t+Δt)。在已知O点气相粒子运动速度VO,g(t)的情况下，可通过气相湍流速度的拉格朗日时间自相关关系给出气相粒子在F点的瞬时速度VF,g(t+Δt)，再通过气相瞬时运动速度的欧拉空间关联，求得P点的气相速度。

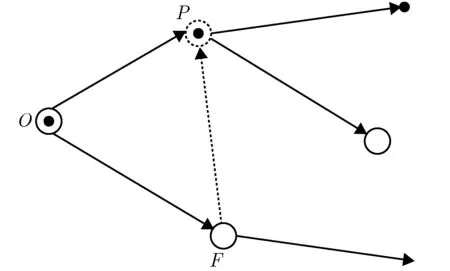
图1双拉格朗日方法示意图Fig.1Sketch of Lagrangian-Lagrangian simulation approach

2计算方法

在两相流模拟中，气相粒子在t时刻的位置为

(4)

其中，vg,x(x,y,z,t-Δt)、vg,y(x,y,z,t-Δt)和vg,z(x,y,z,t-Δt)分别为t-Δt时刻气相粒子在x、y、z坐标方向的速度分量。在湍流场中，气相的速度由平均速度和脉动速度组成，即

(5)

(6)

其中，σx、σy和σz分别为脉动风速在x、y、z坐标方向的标准差；ξ是一个由计算机产生的标准正态分布随机数；RL,x、RL,y和RL,z分别为x、y、z坐标方向的拉格朗日自相关系数：

(7)

其中，TL,x、TL,y和TL,z分别是x、y、z坐标方向的拉格朗日相关时间尺度。

另外，在同一时刻不同位置上的湍流速度，可以采用与式(6)类似的欧拉关联计算：

(8)

其中，RE，x、RE，y和RE，z分别为x、y、z坐标方向的欧拉相关系数，由欧拉时间尺度通过与式(7)类似的关系计算得到。拉格朗日相关时间尺度和欧拉相关时间尺度之比β可表示为

(9)

其中，i为湍流强度，可表示为

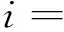
(10)

颗粒在气流中运动时，主要受到重力G、黏性阻力FD、Basset力FB、Magnus力FM、附加质量力Fmv、Saffman升力FS和压力梯度力Fp的作用。假设颗粒为不变形、无相互碰撞的球形颗粒，其存在对流体相无影响，那么，颗粒在边界层中运动的受力关系为

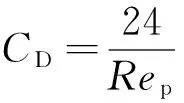
(12)

基于上述方法，编制了颗粒物在气流中运动的气固两相流模拟程序。该程序能够计算不同粒径颗粒物在已知平均流场时空分布的气流中的运动情况，程序流程图如图2所示。其中，Vg(Xg,t+Δt)和Vg(Xp,t+Δt)分别为气流在Xg(t+Δt)和Xp(t+Δt)处的运动速度。

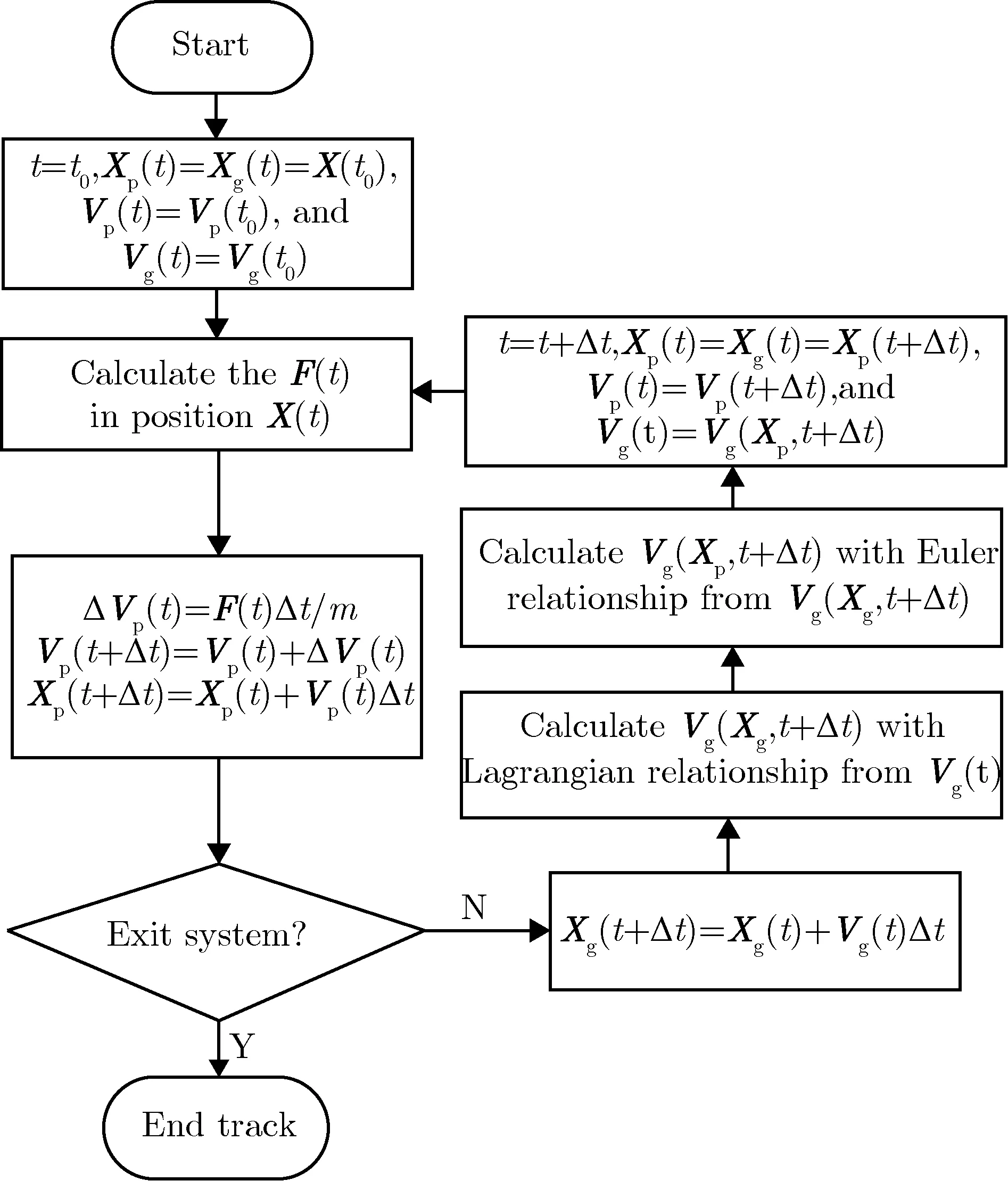
图2双拉格朗日程序流程图Fig.2The flow chart of Lagrangian-Lagrangian simulation code

3结果及分析

为了验证上述方法的正确性，对1997年Tanière等所做的颗粒物扩散实验进行了模拟计算。Tanière实验研究了玻璃粒子和聚氯乙烯(PVC)粒子在平板边界层中的扩散过程[10]。该实验中气相自由速度Ve=10.6 m·s-1, 摩擦速度V*= 0.4 m·s-1，玻璃粒子直径dglass=60 μm，密度ρglass=2 500 kg·m-3，PVC粒子直径dPVC=130 μm，

密度ρPVC=1 430 kg·m-3，颗粒物在离平板端点3.17 m处从平板底部进入流场，释放初始速度vy0为2.0V*～2.5V*，入射角度α为15°～45°。根据实验测量参数，实验中的一些物理量分布如下[11]：

边界层厚度：

(13)

边界层速度分布：

(14)

拉格朗日相关时间尺度：

(15)

边界层内湍流速度的标准差：

(16)

此外，计算中涉及的空气密度ρa为1.19 kg·m-3，空气动力黏度μ为1.81×10-5Pa·s，重力加速度g为9.81 m·s-2。计算中粒子碰壁过程按弹性碰撞处理。

表1为颗粒物在离平板端点5 m处的受力情况。计算Magnus力FM时，颗粒的转速取1 000 r·s-1。由于Saffman升力FS和压力梯度力Fp的大小与颗粒到边界的距离密切相关，因此表中同时给出了粒子所在高度为0.01δ(x)，0.1δ(x)和0.5δ(x)时FS和Fp的值。从表1可以看出，在上述给定的物理特征参数下，玻璃和PVC颗粒在平板边界层中的运动行为，主要受气流黏性阻力和Basset力的支配，但由于重力方向始终竖直向下，重力累积效应导致的粒子沉降也不可忽略。另外，当颗粒比较接近边界位置时，气流在垂直方向有较大的速度梯度，此时，颗粒受到的Saffman升力FS和压力梯度力Fp会明显增大，且这两种力的方向始终竖直向上，FS约比Fp大1个数量级，因此，在边界层中，Saffman力是使颗粒物不发生沉降的主要作用力。

表1颗粒物受到各种力的大小

图3为玻璃粒子和PVC粒子的运动轨迹。从图中可以看出，两种粒子在边界层底部做跳跃运动，只有个别粒子能够进入主流区。PVC粒子的运动轨迹类似在重力作用下的抛物线，而玻璃粒子由于质量较小，惯性效应较弱，运动更容易受湍流波动的影响，因此轨迹明显偏离只有重力作用时的抛物线运动，表现出较强的随机性。

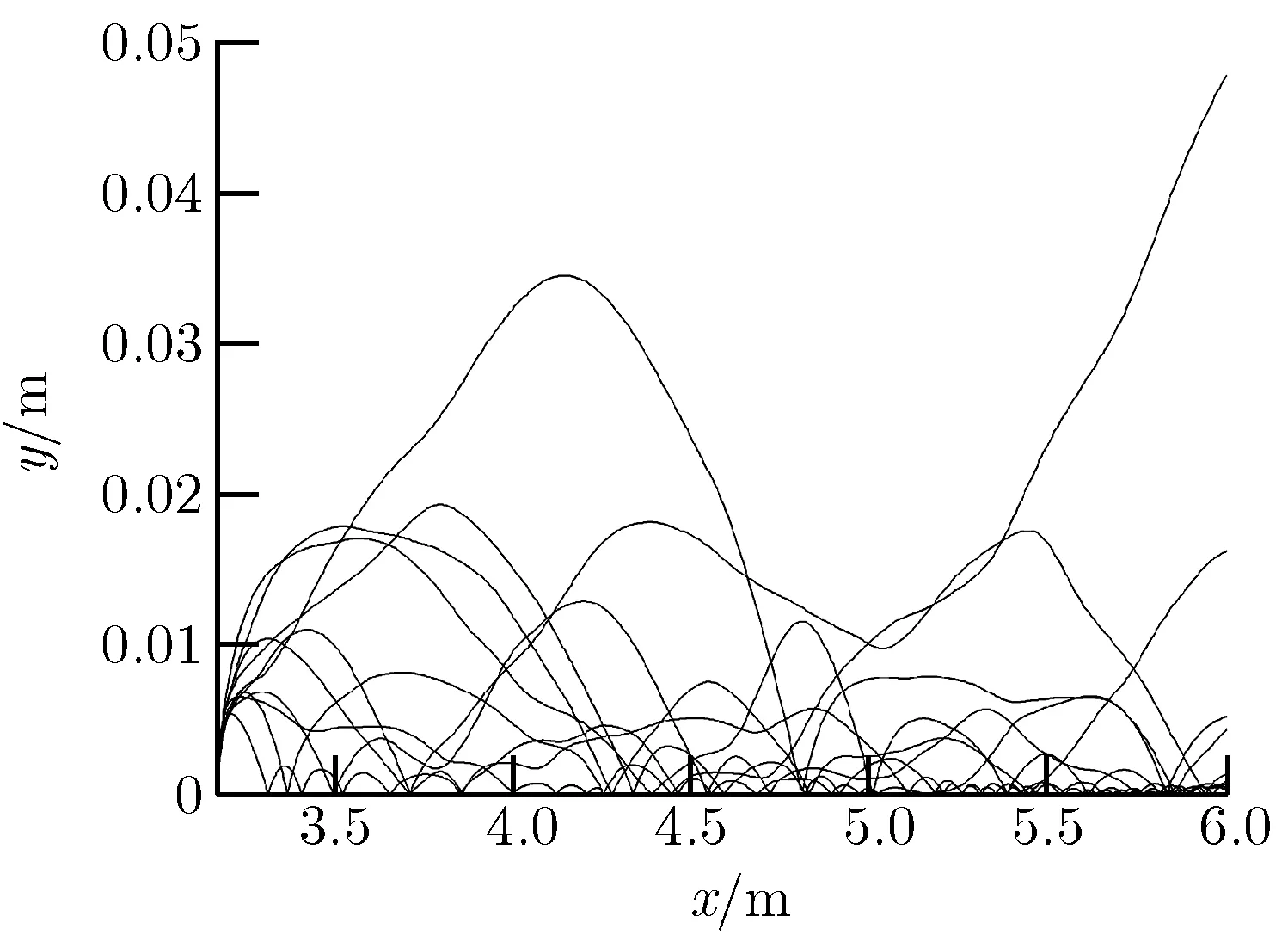
(a)Glass

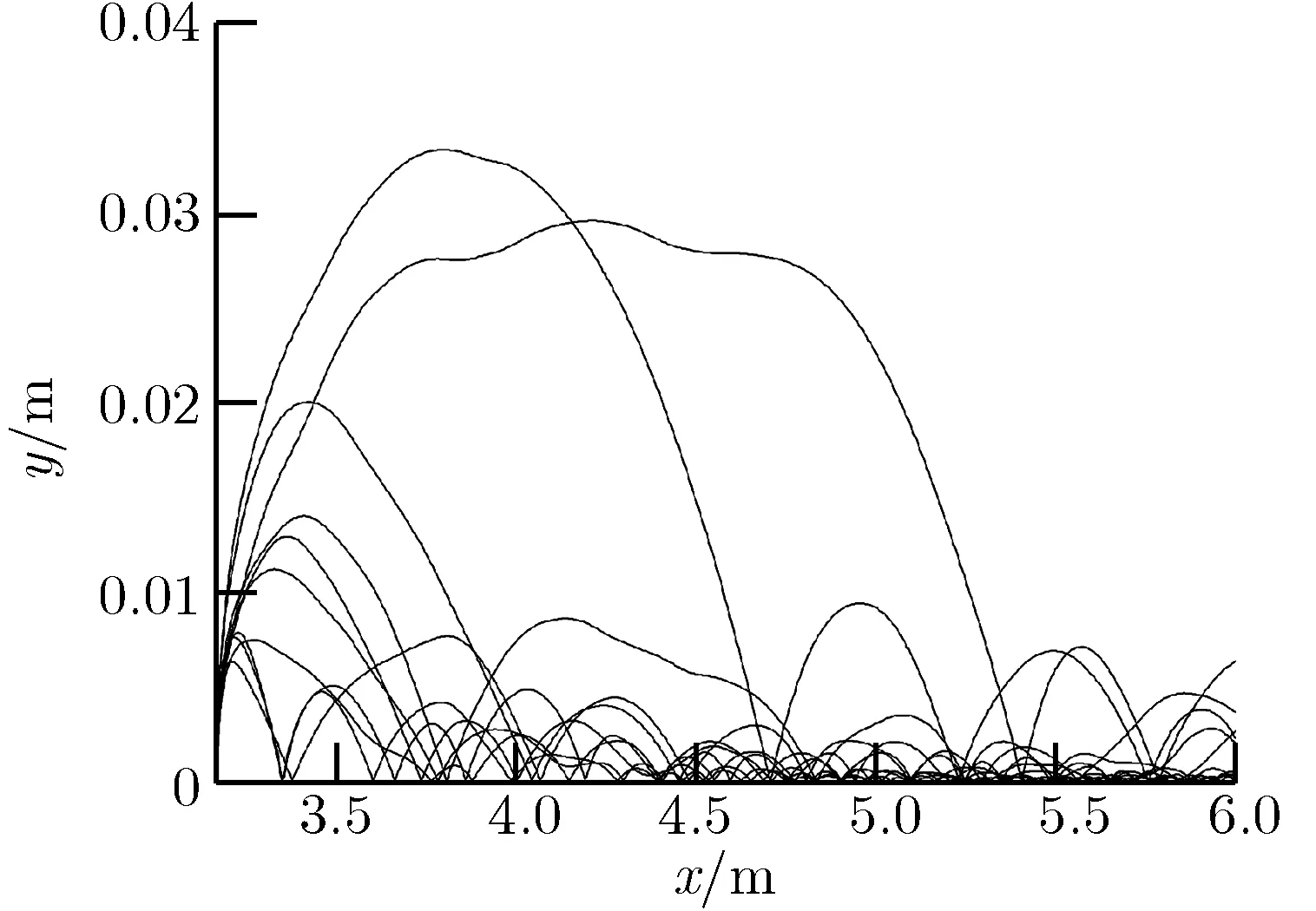
(b)PVC图3粒子轨迹Fig.3Particle traces

跟踪模拟计算了10 000个粒子在边界层中的运动轨迹，图4给出了离平板端点5.06 m处颗粒物质量通量Φm随离开壁面法向无量纲距离y+的变化情况，并将模拟计算结果与文献[10]的实测结果进行了比较。其中，y+可表示为

(17)

从图4可以看出，计算结果与实验结果符合较好，变化趋势也基本一致，初步验证了本文方法在颗粒物扩散计算中的可行性。但图4中的计算结果与实验值还存在一定的偏差。引起偏差的原因可能是在本文的计算中忽略了颗粒间的碰撞。此外，由于目前对湍流的认识不足，计算中采用的湍流特征参数与实验中的实际情况可能存在偏差。

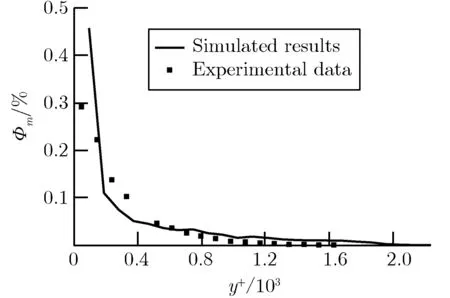
(a)Glass

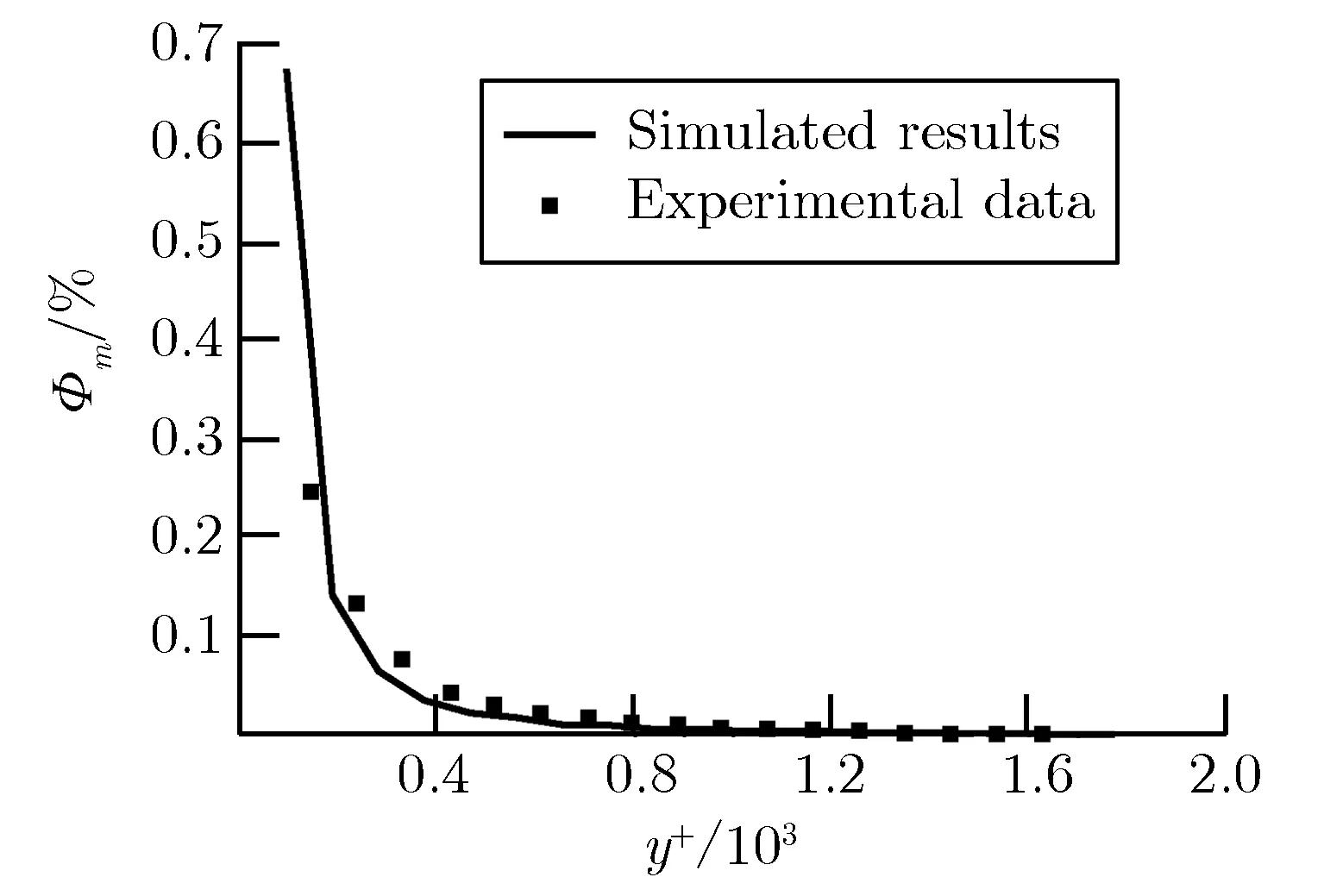
(b)PVC图4质量通量随y方向无量纲距离y+的变化Fig.4Mass flux vs. y+

4小结

建立了一种对气相和固体颗粒均采用拉格朗日方法模拟的双拉格朗日粒子扩散计算模型。在计算气相流动时，用拉格朗日自相关关系计算相同粒子在不同时刻的湍流速度，用欧拉关联描述不同位置上的气相粒子在同一时刻的湍流速度关系；使用牛顿运动方程描述固体颗粒物在流体中的运动行为，考虑了颗粒物在流体中受到的黏性阻力、Saffman升力、Basset力及重力的影响。依据该模型编写了计算程序，模拟了颗粒物在平板边界层的运动，并将计算结果与文献的实验结果进行了比较。分析认为：计算结果与文献实测结果吻合良好。

[1]李静海, 欧阳洁, 高士秋, 等. 颗粒流体复杂系统的多尺度模拟[M]. 北京: 科学出版社, 2005.(LI Jing-hai, OUYANG Jie, GAO Shi-qiu, et al. Multi-Scale Simulation of Particle-Fluid Complex Systems[M]. Beijing: Science Press, 2005.)

[2]WANG X M, DONG Z B, ZHANG J W, et al. Relations between morphology, air flow, sand flux and particle size on transverse dunes, Taklimakan sand sea, China[J]. Earth Surface Processes and Landforms: The Journal of the British Geomorphological Research Group, 2002, 27(5): 515-526.

[3]危卫, 鲁录义, 顾兆林. 风沙运动的电场-流场耦合模型及气固两相流数值模拟[J]. 物理学报, 2012，61(15): 158301. (WEI Wei, LU Lu-yi, GU Zhao-lin. Modeling and simulation of electrification of wind-blown-sand two-phase flow[J]. Acta Phys Sin, 2012, 61(15): 158301.)

[4]马银亮. 高浓度气固两相流的数值模拟研究[D]. 杭州: 浙江大学, 2001.(MA Yin-liang. Study on numerical simulation of dense gas-particle two-phase flow[D]. Hangzhou: Zhejiang University, 2001.)

[5]刘向军, 石磊, 徐旭常. 稠密气固两相流欧拉-拉格朗日的研究现状[J]. 计算力学学报, 2007, 24(2): 166-172.(LIU Xiang-jun, SHI Lei, XU Xu-chang. Activities of dense particle-gas two-phase flow modeling in Eulerian-Lagrangian approach[J]. Chinese Journal of Computational Mechanics, 2007, 24(2): 166-172.)

[6]昌泽舟, BERLEMONT A, GOUESBET G. 气固两相流中颗粒弥散的拉格朗日模拟[J]. 计算力学学报, 2001, 18(3): 284-289.(CHANG Ze-zhou, BERLEMONT A, GOUESBET G. Lagrangian simulation of particle dispersion in gas-solid turbulent flows[J]. Chinese Journal of Computational Mechanics, 2001, 18(3): 284-289.)

[7]CHEN B, WANG C, WANG Z W, et al. Investigation of gas-solid flow across circular cylinders with discrete vortex method[J]. Applied Thermal Engineering, 2009, 29(8/9): 1 457-1 466.

[8]THOMSON D J. Criteria for the selection of stochastic models of particle trajectories in turbulent flows[J]. J Fluid Mech, 1987, 180: 520-556.

[9]CLIFT R, GRACE J R, WEBER M E. Bubbles, Drops and Particles[M]. New York: Academic Press, 1978.

[11]郭宇, 崔桂香, 许春晓, 等. 湍流边界层中重粒子弥散的随机模型[J]. 计算物理, 2004, 21(6): 515-522.(GUO Yu, CUI Gui-xiang, XU Chun-xiao, et al. A stochastic model of heavy particle dispersion in turbulent boundary layer[J]. Chinese Journal of Computational Physics, 2004, 21(6): 515-522.)

Lagrangian-Lagrangian Simulation of Gas-Solid Two-Phase Flow in Turbulent Boundary Layer

ZHUO Jun,HUANG Liu-xing,NIU Sheng-li,XIE Hong-gang

(Northwest Institute of Nuclear Technology,Xi’an710024,China)

A Lagrangian-Lagrangian simulation approach of gas-solid two-phase flow in boundary layer with turbulence is presented, and the reliability verification of the approach is also provided in this paper. In the Lagrangian-Lagrangian simulation approach, both gas and solids are simulated in Lagrangian model. The gas is transported under mean wind, meanwhile, the influence of turbulence is dealt with a series of random movements of gas. The velocities of turbulence sequence in time are simulated by Lagrangian relationship, and velocities of turbulence at different positions are determined by Eular relationship. The particle traces are determined by solving Newtonian equations of motion. The forces such as drag forces, Magnus forces, Basset forces and gravity are considered when particles move in gas flow. The proposed model is applied to simulating a horizontal turbulent boundary layer of air carrying heavy solid particles. The values of forces imposed on particles and the images of particle traces during transportation are obtained. The calculated results of mass flux of particles have been compared with the experimental data, and they are in good agreement.

gas-solid two-phase flow;solid particles;turbulence;diffusion;Lagrangian-Lagrangian

2016-07-04；

2016-07-18

卓俊(1982-)，男，浙江龙泉人，助理研究员，硕士，主要从事放射性核素大气扩散数值模拟研究。

E-mail:zhuojun@nint.ac.cn

O359

A

2095-6223(2016)031004(6)