PID控制器与CFD的耦合模拟技术研究及应用

陈琦， 郭勇颜， 谢昱飞， 陈坚强， 袁先旭

中国空气动力研究与发展中心 计算空气动力研究所， 绵阳　621000



PID控制器与CFD的耦合模拟技术研究及应用

陈琦， 郭勇颜， 谢昱飞*， 陈坚强， 袁先旭

中国空气动力研究与发展中心 计算空气动力研究所， 绵阳621000

飞行控制系统(FCS)与计算流体力学(CFD)的耦合求解是一个崭新的研究领域。传统的飞行控制系统的工程仿真方法依靠气动力模型或气动力数据库得到不同飞行姿态的气动力；而当前方法通过耦合求解Navier-Stokes方程和刚体动力学方程(RBD)以获取飞行器运动过程实时流场和非定常气动力。由于充分反映了气动力的非定常、非线性效应，因而从根本上保证了飞行控制系统仿真的精度。以方形截面导弹俯仰姿态控制为例，首先给出了系统的传递函数，并基于系统在单位阶跃舵偏操纵下的开环响应特性，提出了传递函数的修正方法，进而设计了该外形俯仰姿态控制的PID控制器。数值模拟了不同控制参数时，P控制器、PD控制器和PID控制器的控制效果。针对不同的控制指令，根据建立的控制律，数值模拟了飞行器在PID控制器作用下的实时响应过程，最终成功实现了对飞行器的俯仰姿态控制。研究发现，当飞行器作慢速机动时，工程仿真与CFD数值计算的结果吻合很好，两种方法可以互相验证；但快速机动时，两种方法给出的结果差异明显，基于CFD的耦合模拟方法由于模拟了飞行器运动和舵面偏转导致的非定常流动过程，其结果比基于静态气动力的工程方法的可靠性更高。在大攻角和快速机动等非定常效应较强时，采用CFD方法评估和验证飞行控制系统是很有必要的。

PID控制器； 数值虚拟飞行； CFD/RBD/FCS耦合模拟； 快速机动； 数值模拟

现代军用飞行器越来越强调机动性和敏捷性。飞行器在快速机动时，气动力有严重的非定常迟滞效应，给控制系统的设计带来了挑战。目前，用于飞行控制系统(FCS)设计和评估的手段主要是传统的飞行仿真方法，通过风洞试验或数值模拟获取不同来流参数和不同飞行状态下的静态气动力，建立气动力数据库或气动力数学模型，进而设计控制律，分析和评估飞行器在控制系统作用下的飞行品质[1-3]。传统方法没有或很少考虑气动力的非定常特性，这在飞行器小攻角飞行或机动性要求不高时影响不大，但当飞行器作快速机动时，控制系统的设计就必须考虑这种影响。

如何有效评估气动力的非线性、非定常效应在大攻角或快速机动时对控制系统的影响，半实物、实物仿真和模型自由飞试验是一种选择，但都存在成本高昂的问题。而随着计算流体力学(CFD)的快速发展和计算机硬件水平的提高，通过耦合求解CFD与FCS获取飞行器闭环响应特性，正成为评估飞行控制律的另一有效手段。

这一涉及CFD、飞行力学和控制理论的多学科交叉技术，有时也称之为数值虚拟飞行技术[4-5]，它的实现有3个关键的技术点：① CFD与飞行力学的耦合求解技术(CFD/RBD耦合)；② 解决控制舵与飞行器本体之间相对运动的动网格技术；③ CFD与控制系统的耦合模拟技术(CFD/FCS耦合)。

3个关键技术中，动网格技术[6-7]经过几十年的沉淀，技术相对成熟。但是在一些复杂情形下，如当舵面与飞行器之间的相对运动导致网格拓扑关系发生变化时，当前的动网格技术仍然不能进行很好地处理，有时甚至需要人工干预。另外由于每个时间步都需要不断地“寻点”，计算效率低下的通病很难从根本上解决。近十多年中，CFD/RBD耦合求解问题在国内外都取得了较大的进展[8-13]，发展了松耦合、紧耦合以及全耦合等耦合方式[14]，解决了一定的工程应用问题，且目前仍处于蓬勃发展时期。设计控制律以及如何将控制律应用于CFD模拟，在当前的CFD研究领域中比较少见，零星的文献虽涉及相关的研究工作，但不够系统[15-16]。这一研究领域正处于刚刚开始发展的阶段。

本文在将CFD/RBD耦合模拟和动网格技术实现的基础上，重点研究控制律的设计和与CFD的耦合模拟技术。以方形截面导弹俯仰姿态控制为例，从古典控制论出发，给出了攻角与舵偏角的传递函数，并通过CFD模拟获取系统的开环响应特性，据此给出系统传递函数的修正方法。在此基础上，设计了满足工程应用需求的PID控制器，通过CFD模拟，开展了控制器各项参数对闭环系统响应特性的影响研究。最后，以工程仿真结果为参考，通过模拟常规机动过程，校核了CFD计算方法，同时将设计的控制器应用于各种机动动作的数值模拟，取得了预期的成效；而通过模拟快速机动过程，开展了气动力非定常效应对控制系统的影响研究。

1　研究方法

以俯仰运动的姿态控制为例展开研究，图1为其实现框图。首先，陀螺仪测量飞行器的实际俯仰姿态角θ，并与给定的姿态角θc进行比较，产生误差信号r；误差信号经过控制器(控制律)处理，产生控制舵偏信号δc，并传递给舵面执行机构；舵面伺服系统推动舵面偏转，产生实际的舵偏角δe；舵面的偏转使飞行器获得附加的俯仰力矩，促使飞行器获得一个新的俯仰姿态，并被送回到闭环系统中。如此反复进行，直到达成控制目的。

图1　飞行器俯仰姿态闭环控制框图Fig.1　Block diagram of closed-loop control for pitching attitude of vehicle

图1中，飞行器系统以俯仰角对舵偏角的传递函数形式表示，可直接得到飞行器俯仰角对舵偏角的响应，这是工程上常用的方法；也可根据静态气动力数据库，通过插值获取不同状态的气动力/力矩，再结合刚体运动方程获取飞行器对舵面运动的响应。除此之外，可直接利用本文所介绍的方法，通过耦合求解CFD与刚体动力学方程，获取飞行器的实时响应过程，再结合PID控制器，获取闭环姿态控制过程。

采用数值求解Navier-Stokes方程的方式获取飞行器气动力系数和飞行器的运动流场，若不考虑网格变形，其空间离散后可写成如下半离散形式：

(1)

式中：守恒变量Q=[ρρuρvρwρe]T；ρ为来流密度；u、v和w分别为笛卡儿坐标系下的速度分量；e为单位体积的总内能；余项R(Q)为

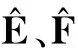
在古典控制论中，系统的数学模型是以传递函数的形式给出，即为系统输出量的拉普拉斯变换与输入量的拉普拉斯变换之比。对于本文所研究的问题，系统的输出量为攻角α(t)，输入量为舵偏角δ(t)，则其传递函数形式为

(2)

式中：s为拉普拉斯算子。

若只考虑俯仰姿态控制问题，则攻角对舵偏角的传递函数可以用飞行器的短周期近似传递函数给出[18]，即

(3)

式中：各项系数为

(4)

若记来流密度和速度分别为ρ和u0，参考长度和参考面积分别为L和S，飞行器质量为m，绕y轴(美式坐标)的转动惯量为Iy，并记

(5)

则式(4)中的各项导数写成气动力系数表示的形式，并转化到风轴系下有

(6)

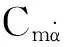
(7)

式中：δc(s)为PID控制器输出的控制舵偏量；δe(s)为伺服机构的实际舵偏量。在数值模拟时，暂未考虑伺服机构的影响。控制器(这里选用常用的PID控制器)的传递函数的表达式为

(8)

式中：r(s)为控制目标和实际飞行姿态的偏差，作为PID控制器的输入；kP、kD和kI为控制器参数。kP、kD和kI的选择又称为参数整定，常用的有Ziegler-Nichols(Z-N)方法[3]等，具体细节不再详述。图2给出了整个PID控制器设计过程的完整框图。

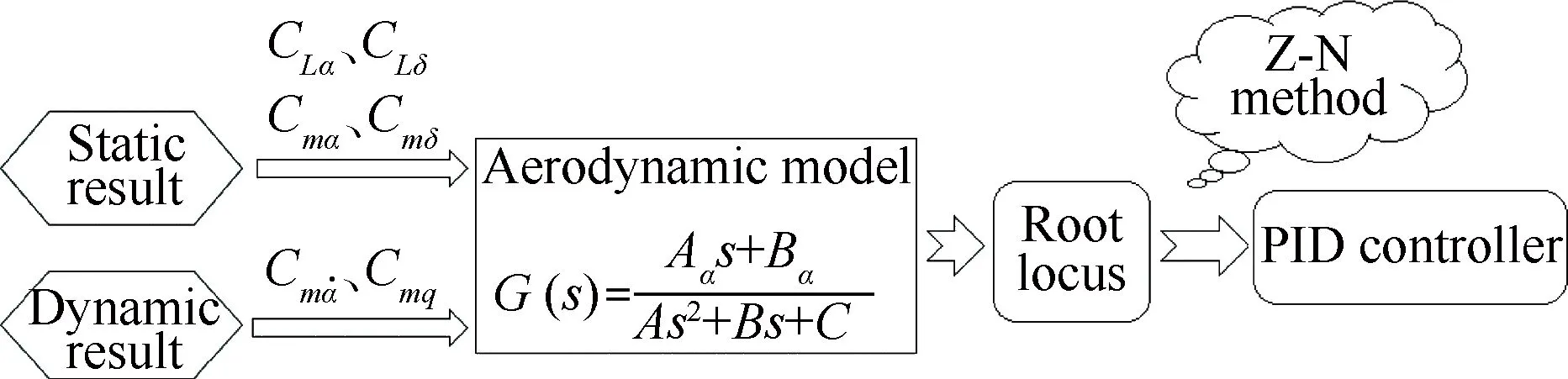
图2　PID控制器设计框图Fig.2　Block diagram of PID controller design

2　俯仰运动的传递函数及修正

本文所研究的对象为方形截面的导弹外形，它由一个圆弧形头部和方形截面的弹身组成[21]。弹身总长为13D，D =93.98mm；头部为切线圆弧，长为3D，圆弧半径R=6.717D；弹身截面为1D×1D的正方形；弹身尾部有4片“十”字布局的三角小翼，小翼的长和高均为1D，宽为0.1D。其模型和表面网格见图3。图4为运用动网格技术生成的升降舵不同舵偏角下的网格比较，其中舵面后缘下偏时定义舵偏角为正，产生低头的俯仰力矩。

图3　方形截面导弹模型和表面网格Fig.3　Model of square cross-section missile and surface grids

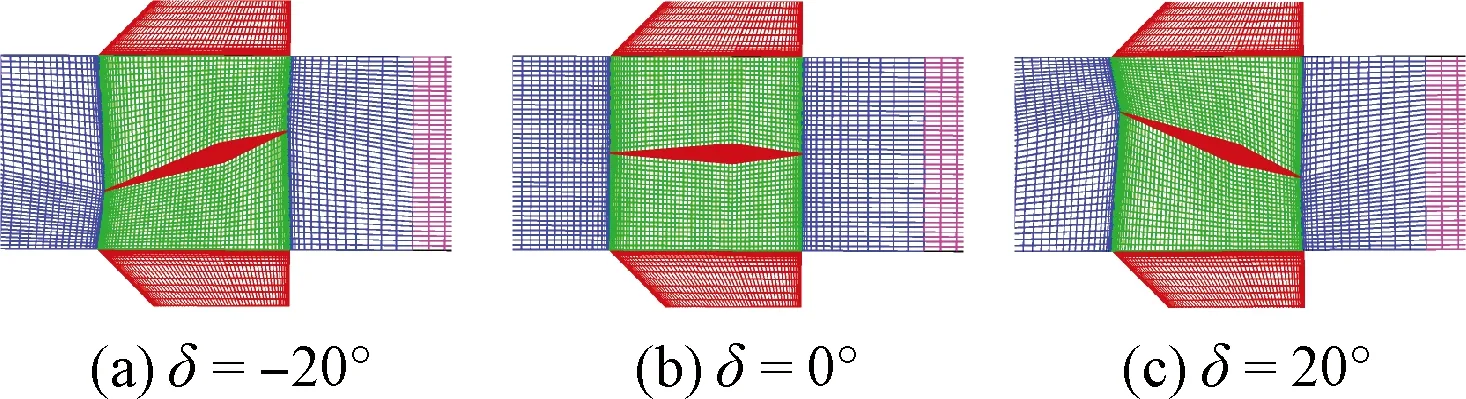
图4　动网格技术生成的不同舵偏角下的网格比较Fig.4　Contrast of grids at different rudder defection angles using dynamic grid technology

定义导弹的俯仰轴为xc=6.11D，升降舵舵轴为x0=11.5D。参考长度L=D，参考面积S=D2。导弹的质量取为10kg，俯仰主转动惯量取为10kg·m2。计算来流马赫数均为Ma=2.5，以弹体全长为参考长度的雷诺数为Re=1.6×107。图5为攻角14° 时，计算得到的空间流线和不同截面位置的压力系数Cp的分布云图，计算结果很好地刻画了导弹周围的流动分离结构。

图6为升力系数CL和俯仰力矩系数Cm随攻角和舵偏角的变化曲线；图7为强迫俯仰振动时俯仰力矩系数随俯仰角的迟滞曲线，振幅为1°，振动频率为1Hz。

图5　导弹周围的流动分离结构Fig.5　Flow separation structure around missile

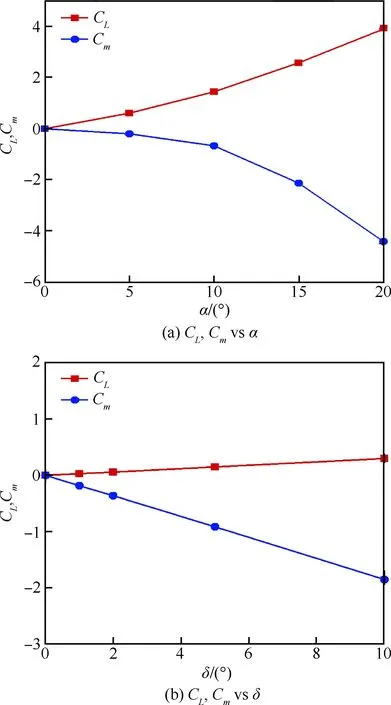
图6　升力系数和俯仰力矩系数随攻角和舵偏角的变化情况Fig.6　Variations of lift coefficient and pitching moment coefficient with respect to angle of attack and rudder deflection angle

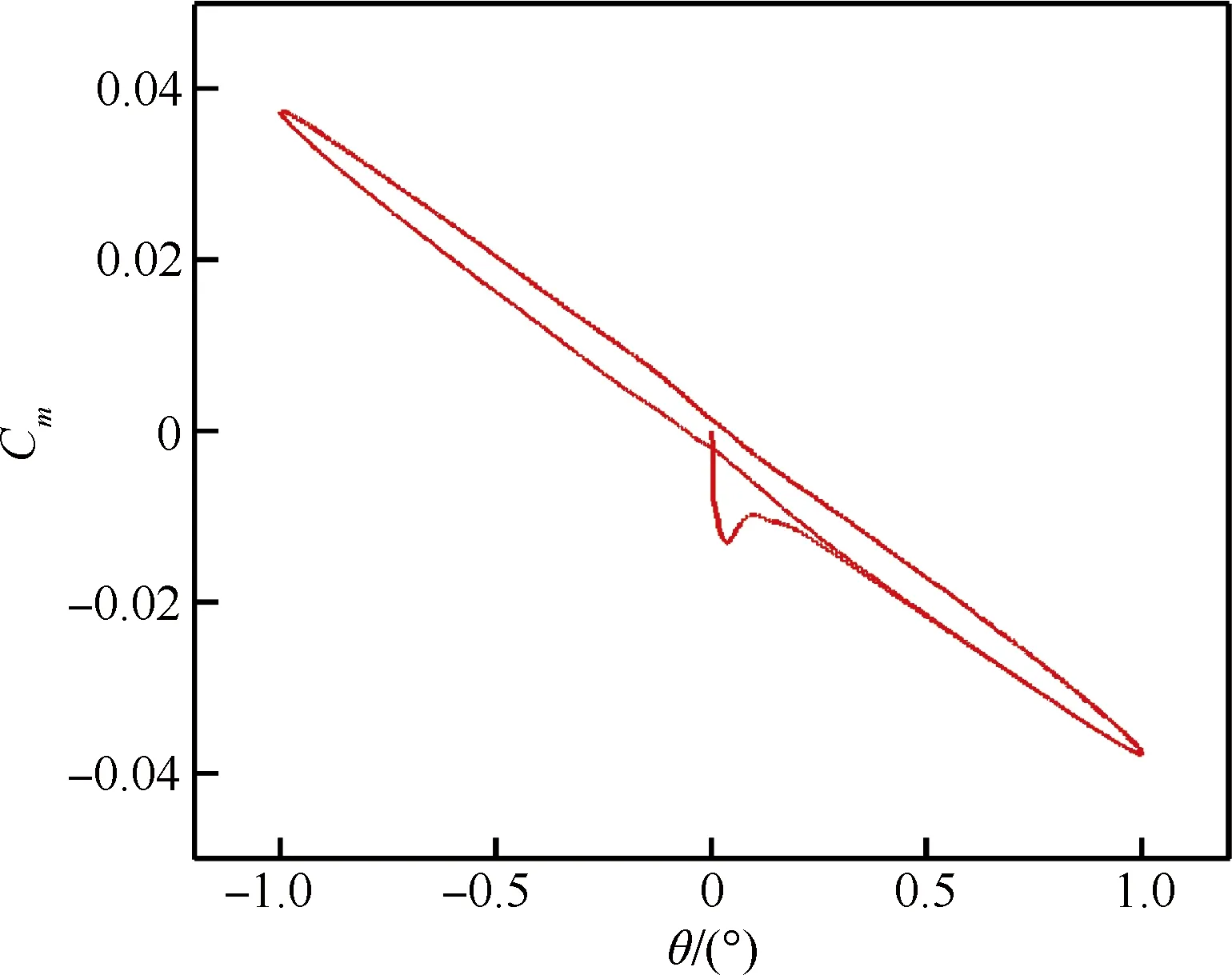
图7　俯仰角-俯仰力矩系数迟滞圈Fig.7　Lag loop of pitching moment coefficient topitching angle

据此，可分别求出在0° 平衡攻角附近的各项气动力系数导数，其中：CLα=7.0、CLδ=1.7、Cmα=-2.2、Cmδ=-10.6、Cmq=-87.4。将导弹的来流参数、质量特性参数和以上导数代入式(3)～式(6)，即可求出0° 攻角时导弹的攻角对舵偏角的传递函数为

(9)

基于此传递函数，可以采用仿真的方法分析系统的响应特性，亦可进行控制系统的设计。图8 为系统在单位阶跃舵偏操纵下攻角的响应曲线。其中，标记为Simulink-m0的曲线为基于上述传递函数采用工程软件MATLAB-Simulink工具箱进行仿真的结果，而标记为CFD的曲线则为采用CFD数值计算的方式，在每个时间步内根据新的飞行姿态求解飞行器实时运动的非定常流场，所得到的飞行器运动的响应曲线，其模拟结果比依靠传递函数仿真的结果可靠性更高。

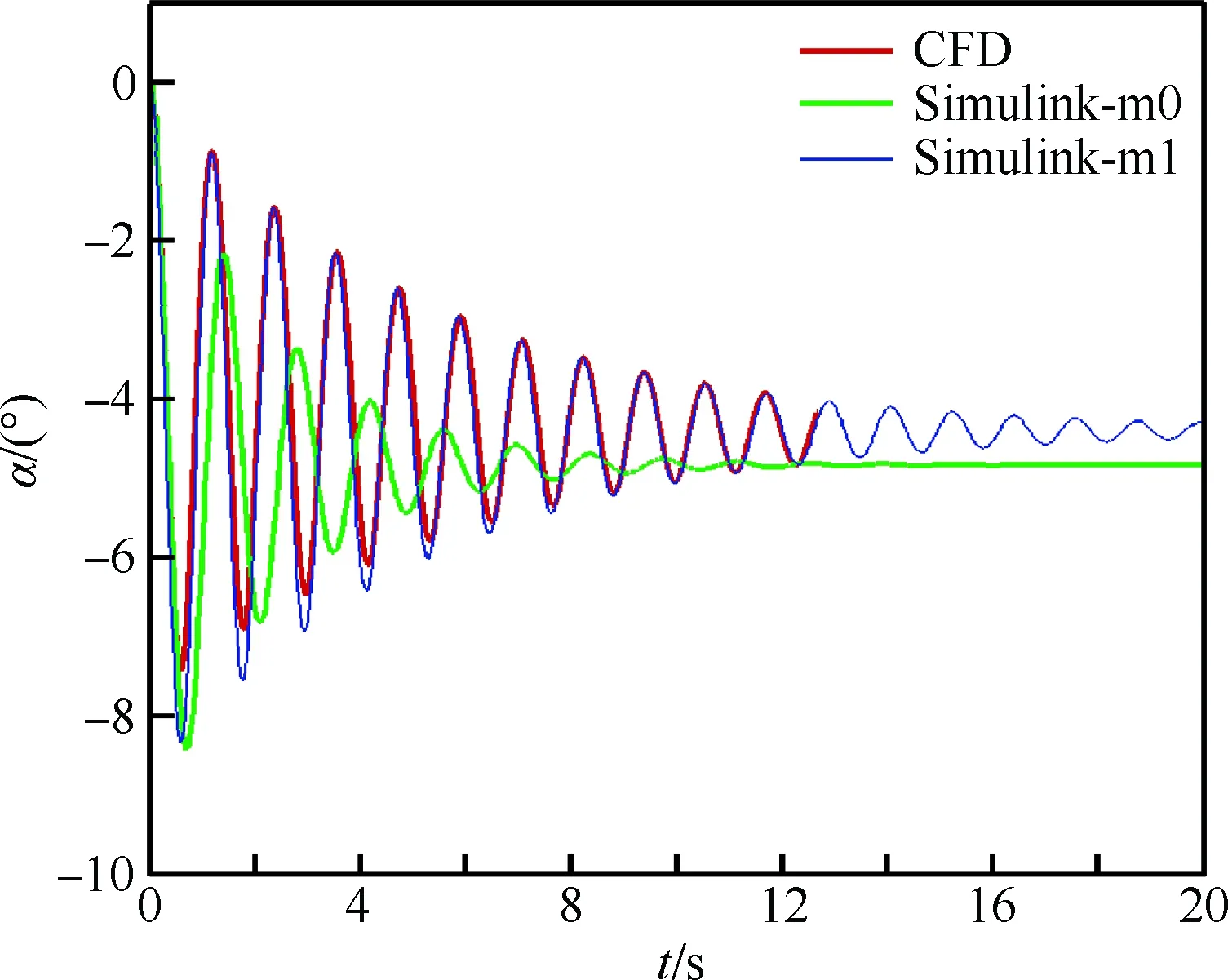
图8　单位阶跃舵偏下的开环控制响应特性Fig.8　Response of open-loop control under step rudder deflection

在图8中，仿真得到的曲线与CFD计算得到的曲线之间的差别很大，因此需要对式(9)所示的传递函数进行一定的修正。回到式(3)，对一个二阶阻尼系统，其传递函数可以写为

(10)

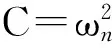
(11)

从而得到Bα=-126.7。最后，根据系统的阻尼特性修正阻尼比ξ，得到2ξωn=0.38，于是修正后的传递函数为

(12)

根据新的传递函数进行仿真，得到图8中的Simulink-m1曲线，可以看出，其与CFD数值计算的结果吻合地很好。但由于导弹系统本身为三阶以上的高阶系统，使用二阶系统近似的结果难免会存在一定的差异，但却可以指导控制律的设计。根据此传递函数，给出了PID控制器的一种参数组合，即

(13)

写成时域中的表达式为

式中：r(t)=α(t)-αc(t)，αc为期望攻角。

3　不同控制器的控制效果比较

PID控制器由比例项、微分项和积分项3项组成，每一项可以单独作用，也可进行两两组合。例如：构成纯比例控制器P，或比例-微分控制器PD，或比例-积分控制器PI；但积分项和微分项一般不单独使用。这里主要考察了P、PD和PID这3种控制器，均采用CFD数值计算，获取动态响应过程。来流状态与前文相同，给定期望的攻角αc均为5°，初始攻角和舵偏角均为0°。

对于比例控制器，参数kP分别取0.5、1.0和2.0，CFD模拟结果如图9所示。根据式(11)，系统的阻尼比ξ值很小，从图8中系统的开环响应模拟结果也可以看到，系统到达到新的配平位置的时间很长，振荡次数很多。而单纯的比例控制器很难调节系统的阻尼特性，同时也存在稳态误差，不能将攻角控制到期望值。记

则系统的稳态误差为

显然，随着kP的增大，系统的稳态误差将逐步降低，这与CFD的模拟结果是一致的。

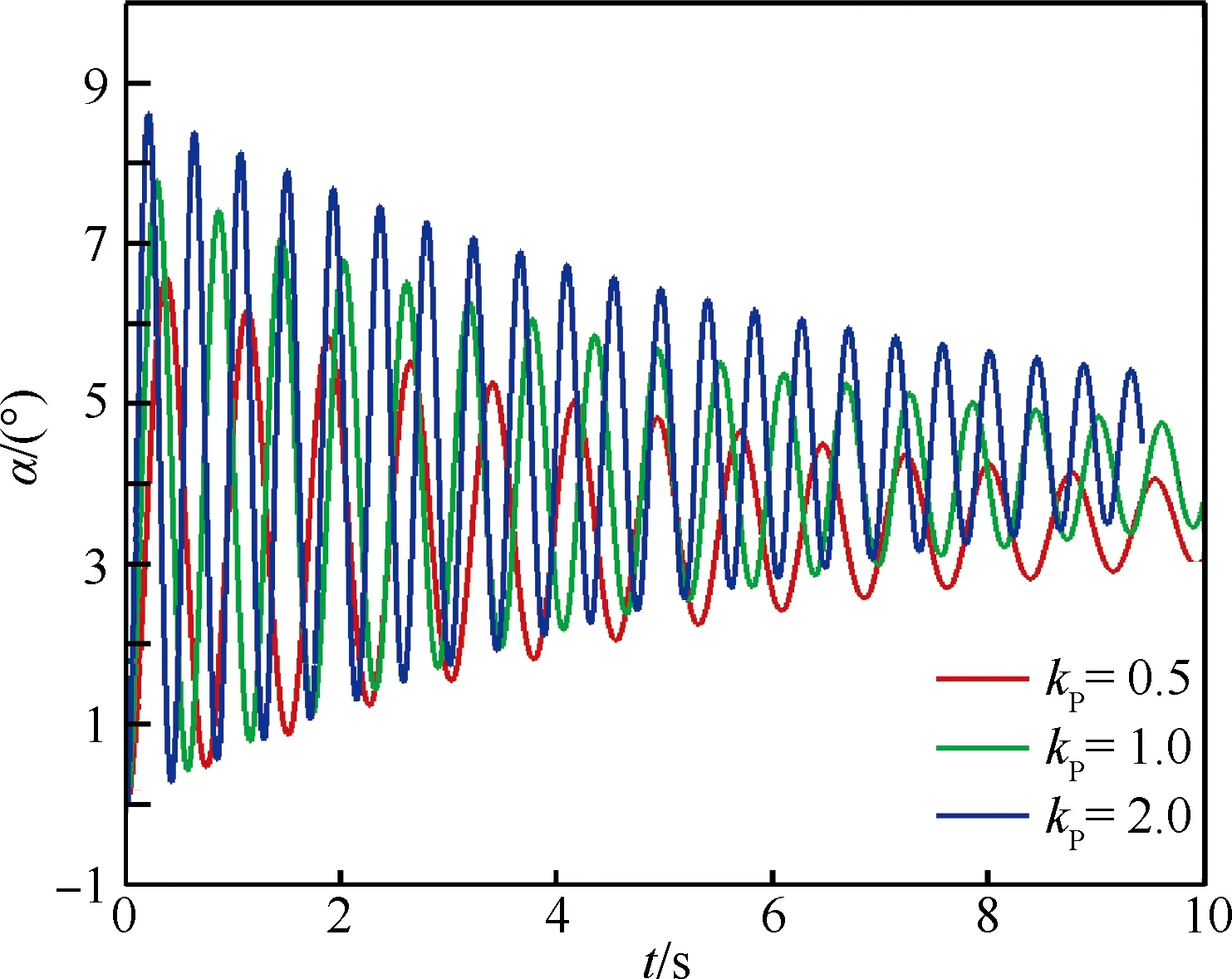
图9　P控制器不同参数下的攻角变化曲线Fig.9　Variation curves of angle of attack under different parameters of P controller

图10为系统对PD控制器响应的数值计算结果，比例项kP=0.5，微分项kD分别取0.05、0.10 和0.20。从模拟结果来看，增加了微分项后，显著地改善了系统的阻尼特性。随着kD从0.05增大到0.20，系统阻尼特性由欠阻尼转变为过阻尼状态。但系统的稳态误差一直存在。

为了消除系统的稳态误差，必须在控制器中加入积分项。控制参数选取为： kP=0.5，kD=0.1，kI分别取1.0、2.0和5.0，图11给出了PID控制器下攻角和舵偏角的响应曲线。从控制效果来看，不同的kI均能将稳态误差消除掉，将攻角控制在期望的5°。但kI过大，系统超调量明显增加，阻尼降低，系统振荡加剧。从舵偏角的响应曲线看，舵偏角最终稳定在-1.2° 附近，实现了控制的目的。

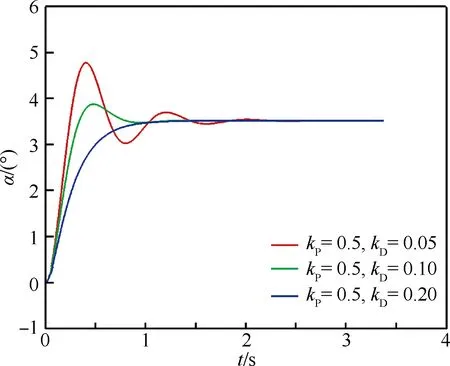
图10　PD控制器不同参数下的攻角变化曲线Fig.10　Variation curves of angle of attack under different parameters of PD controller

图11　PID控制器不同参数下的攻角和舵偏角变化曲线Fig.11　Variation curves of angle of attack and rudder deflection angle under different parameters of PID controller

4　控制律的应用研究

在第3节的研究中，导弹的攻角由0° 阶跃到5°，并不符合真实的物理情况。本节中，设定了几种不同的运动方式，考察控制律的控制效果。计算来流状态不变，但导弹的起始攻角为10°，此时，导弹的配平舵偏角,即初始舵偏角为-4.65°。此时导弹的俯仰姿态控制的传递函数为

(14)

PID控制器为

(15)

期望在5s内将导弹的攻角控制到15°，但实现过程有以下4种方式：阶跃型、直线型、双直线型和正弦函数型：

数值计算的结果如图12所示。由于机动的动作较慢，几种机动动作下，设计的控制律均能完美地实现控制的目的。对于匀速拉升的情况(m2)，由于在拉升末尾阶段仍然存在一个恒定的俯仰角速度，控制器微分项的偏差无法消除，因而到达指定时间时，期望目标与实际值之间有小的偏差。拉升结束后，俯仰角速度消失，控制器很快将导弹攻角控制到15°。

上述模拟结果在导弹机动动作较慢时给出，但当导弹作快速机动时，常常伴随着较强的气动力迟滞效应，控制器的性能受到考验。图13分别给出了机动时间为5.0s、2.0s、1.0s和0.5s时的模拟结果以实线表示，机动动作均为1/4个周期(T)的正弦模式(m4)，图中ω=2π/T为圆频率。为便于比较，图13(b)～图13(d)的时间轴分别放大了相应的倍数。作为对比分析，图13中还给出了基于传递函数的MATLAB的仿真结果以虚线表示。

可以看到，在机动动作较慢时，CFD数值计算结果和工程仿真结果给出了一致性的结果，两种方法可以相互验证。此时控制器的效果也比较好，可以在规定的时间内达成控制目的。随着飞行器机动动作加快，在控制时间从5s变化到0.5s的过程中，两种方法给出的结果均显示，控制器的控制效果逐渐变差，在规定的机动时间内，距离控制目标都有一定的偏差。分析偏差产生的原因，对工程仿真方法，以式(3)表征的传递函数为基础，其实质是一个二阶阻尼系统，控制目标与期望值的偏差反映的是二阶阻尼系统的迟滞效应。而基于CFD的数值计算方法，它实时模拟了飞行器运动和舵面偏转的非定常流动，控制目标与期望值的偏差真实反映了飞行器快速机动时带来的气动力/力矩的迟滞效应。因此，其模拟结果比工程仿真方法具有更高的可信度。同时也可以看出，真实的控制系统迟滞效应比工程方法给出的结果更严重，在飞行器快速机动时，很有必要采用基于CFD数值计算的方法评估飞行器的控制系统。

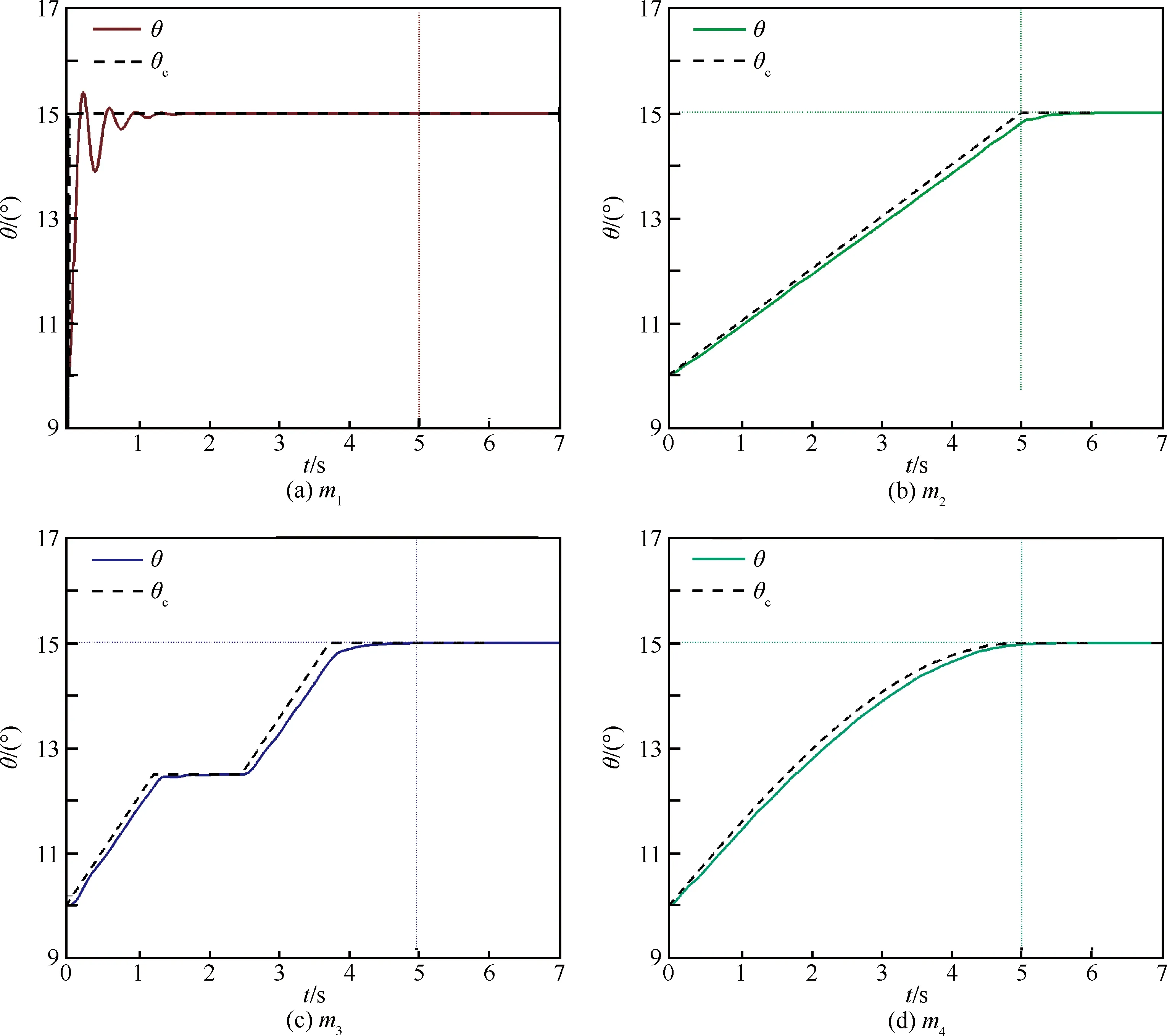
图12　PID控制器对不同控制指令的模拟结果Fig.12　Simulation results of different control commands under PID controller

5　结　论

基于经典控制理论，给出了飞行器俯仰运动的传递函数，设计了PID控制器。分析了PID控制器各项参数的控制效果，研究了不同机动动作和机动时间时控制器的表现。

1) 建立了CFD/RBD/FCS一体化的耦合模拟方法，从建立传递函数出发，到基于开环响应特性的传递函数修正，并设计飞行器的控制律，最终建立了一套完整的耦合模拟体系。

2) 在快速机动时，由于飞行器运动导致的非定常效应增加，相比工程仿真方法，基于CFD的数值计算能提供更可靠的控制系统闭环响应的模拟结果。

3) 受制于CFD计算效率，工程仿真方法仍是当前及未来一段时间内设计和评估控制系统的主要手段，但在关键弹道点，采用基于CFD的方法对控制系统进行验证和评估，是非常必要的。

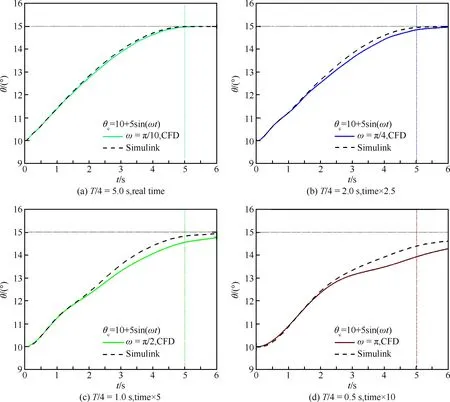
图13　机动时间不同时，CFD计算与工程仿真结果的比较Fig.13　Comparison of results based on CFD with results based on transfer function at different maneuvering time

[1]TAN W Q, EFREMOV A V, QU X J. A citerion based on closed-loop pilot-aircraft systems for predicting flying qualities[J]. Chinese Journal of Aeronautics, 2010, 23(5): 511-517.

[2]刘艳. 总体设计中的飞控系统控制律设计与评估研究[D]. 西安: 西北工业大学, 2006: 2-3.

LIU Y. Research on flight control law designing and evaluating for concept aircraft design[D]. Xi’an: Northwestern Polytechnical University, 2006: 2-3 (in Chinese).

[3]陈云霞, 康锐, 孙宇峰. 导弹飞控系统可靠性仿真研究[J]. 航空学报, 2004, 25(3): 242-247.

CHEN Y X, KANG R, SUN Y F. Study on reliability simulation for missile’s flight control system[J]. Acta Aeronautica et Astronautica Sinica, 2004, 25(3): 242-247 (in Chinese).

[4]MAGILL J C, SHAWN W. Initial test of a wire suspension mount for missile virtual flight testing: AIAA-2002-0169 [R]. Reston: AIAA, 2002.

[5]GLENN G, JOY K, JUAN L. Wind tunnel based virtual flight testing: AIAA-2000-0829[R]. Reston: AIAA, 2000.

[6]NAKAHASHI K, GUMIYA T. An intergrid boundary definition method for overset unstructured grid approach: AIAA-1999-3304[R]. Reston: AIAA, 1999.

[7]BATINA J T. Unsteady Euler airfoil solutions using unstructured dynamic meshes: AIAA-1989-0115[R]. Reston: AIAA, 1989.

[8]FUJII K. Numerical experiment of the flight trajectory simulation by fluid dynamics and flight dynamics coupling: AIAA-1993-3324[R]. Reston: AIAA, 1993.

[9]BUNING P G, GOMEZ R J, SCALLION W I. CFD approaches for simulation of wing-body stage separation: AIAA-2004-4838[R]. Reston: AIAA, 2004.

[10]COSTELLO M, GATTO S, SAHU J. Using CFD/RBD results to generate aerodynamic models for projectile flight simulation: AIAA-2007-6582 [R]. Reston: AIAA, 2007.

[11]SAHU J. Time-accurate numerical prediction of free-flight aerodynamics of a finned projectile: AIAA-2005-5817 [R]. Reston: AIAA, 2005.

[12]杨云军, 崔尔杰, 周伟江. 耦合时间精度对模拟飞行器自由运动特性的影响[J]. 计算物理, 2007, 24(1): 42-48.

YANG Y J, CUI E J, ZHOU W J. Influence of coupling time accuracy on the simulation of aircraft free movement[J]. Chinese Journal of Computational Physics, 2007, 24(1): 42-48 (in Chinese).

[13]陈坚强, 陈琦, 袁先旭, 等. 舵面操纵动态响应的数值模拟研究[J]. 力学学报, 2013, 45(2): 302-306.

CHEN J Q, CHEN Q, YUAN X X, et al. Numerical simulation study on dynamics response under rudder control[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(2): 302-306 (in Chinese).

[14]张来平, 马戎, 常兴华, 等. 虚拟飞行中气动、运动和控制耦合的数值模拟技术[J]. 力学进展, 2014, 44: 376-417.

ZHANG L P, MA R, CHANG X H, et al. Review of aerodynamics/kinematics/flightcontrol coupling methods in virtual flight simulations[J]. Advances in Mechanics, 2014, 44: 376-417 (in Chinese).

[15]ALLAN M R, BADCOCK K J, RICHARDS B E. CFD based simulation of longitudinal flight mechanics with control: AIAA-2005-0046[R]. Reston: AIAA, 2005.

[16]李锋, 杨云军, 刘周, 等. 飞行器气动/飞行/控制一体化耦合模拟技术[J]. 空气动力学学报, 2015, 33(2): 151-161.

LI F, YANG Y J, LIU Z, et al. Integrative simulation technique of coupled aerodynamics and flight dynamics with control law on a vehicle[J]. Acta Aerodynamica Sinica, 2015, 33(2): 151-161 (in Chinese).

[17]谢昱飞. 细长圆锥超声速绕流的非对称分离及其诱导之等角速度锥转运动[D]. 绵阳：中国空气动力研究与发展中心, 2005: 13-21.

XIE Y F. Computation and analysis of asymmetric separations over a slender cone and one induced steady coning motion [D]. Mianyang: China Aerodynamics Research and Development Center, 2009: 13-21 (in Chinese).

[18]ROBERT C N. 飞行稳定性和自动控制[M]. 顾均晓, 译. 北京: 国防工业出版社, 2008: 295-297.

ROBERT C N. Flight stability and automatic control[M]. GU J X, translated. Beijing: National Defense Industry Press, 2008: 295-297 (in Chinese).

[19]陈琦, 陈坚强, 袁先旭, 等. 谐波平衡法在动导数快速预测中的应用研究[J]. 力学学报, 2014, 46(2): 183-190.

CHEN Q, CHEN J Q, YUAN X X, et al. Application of a harmonic balance method in rapid predictions of dynamic stability derivatives[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(2): 183-190 (in Chinese).

[20]刘伟, 杨小亮, 赵云飞. 高超声速飞行器加速度导数数值模拟[J]. 空气动力学学报, 2010, 28(4): 426-429.

LIU W, YANG X L, ZHAO Y F. Numerical simulation of acceleration derivative of hypersonic aircraft[J]. Acta Aerodynamica Sinica, 2010, 28(4): 426-429 (in Chinese).

[21]TREVOR J B, KRISTIAN P. CFD predictions of square and elliptic cross-section missile configurations at supersonic speeds: AIAA-2004-5453[R]. Reston: AIAA, 2004.

陈琦男，博士研究生。主要研究方向： 非定常计算空气动力学。

Tel.: 0816-2463304

E-mail: chenqi@mail.ustc.edu.cn

谢昱飞男，博士，副研究员。主要研究方向： 计算流体力学方法及复杂流动数值模拟等。

Tel.: 0816-2463090

E-mail: xyf_5843@qq.com

Research and application of coupled simulation techniques ofPID controller and CFD

CHEN Qi, GUO Yongyan, XIE Yufei*, CHEN Jianqiang, YUAN Xianxu

Computational Aerodynamics Institute, China Aerodynamics Research and Development Center,Mianyang621000, China

It is a novel research field to couple computational fluid dynamics (CFD) into the simulation of flight control system (FCS). In engineering simulations of FCS, the aerodynamics of the vehicle is given by the aerodynamic models or aerodynamic databases, while in this coupled way, they are obtained by solving the Navier-Stokes equations/rigid body dynamics (RBD) equations. Thus the unsteady and nonlinear portion of the aerodynamics is adequately reserved, which guarantees the accuracy of simulation of the FCS. Taking the control of the pitching attitude of a square cross section missile as an example, the transfer functions about the vehicle motion system are first given, and modifications to transfer functions are conducted based on the open-loop response characteristics of the system to unit step fin-deflection maneuver, then the PID controller for the control of the pitching attitude of the vehicle is designed. Control effects about the P, PD and PID controller are numerically investigated with various control parameters. According to different control commands, the real-time response process of the vehicle under the PID controller is numerically simulated and the attitude control of pitching motion of the vehicle is finally reached. The investigation shows that when the maneuver action is slow, the simulation results based on CFD show good agreement with those based on the engineering simulation, while when the maneuver action is rapid, the two results have significant differences. The present method, which simulates the unsteady flow process induced by the vehicle motion and the fin-deflection, is more reliable than the engineering simulation method based on static aerodynamics. This indicates that it is of great necessity to predict and validate the FCS utilizing CFD method in the case of strong nonlinear effects including high angles of attack and rapid maneuver.

PID controller; numerical virtual flight; CFD/RBD/FCS coupling simulation; rapid action; numerical simulation

2016-01-19； Revised： 2016-02-15； Accepted： 2016-03-22； Published online： 2016-04-0517:02

s： National Natural Science Foundation of China (11172315, 91216203, 11372341, 11532016)

. Tel.： 0816-2463304E-mail: xyf_5843@qq.com

2016-01-19； 退修日期： 2016-02-15； 录用日期： 2016-03-22；

时间： 2016-04-0517:02

www.cnki.net/kcms/detail/11.1929.V.20160405.1702.006.html

国家自然科学基金 (11172315, 91216203, 11372341, 11532016)

.Tel.： 0816-2463090E-mail: xyf_5843@qq.com

10.7527/S1000-6893.2016.0093

V211.3

A

1000-6893(2016)08-2507-10

引用格式： 陈琦， 郭勇颜， 谢昱飞， 等． PID控制器与CFD的耦合模拟技术研究及应用[J]． 航空学报, 2016, 37(8): 2507-2516. CHEN Q, GUO Y Y, XIE Y F, et al. Research and application of coupled simulation techniques of PID controller and CFD[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2507-2516.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

URL： www.cnki.net/kcms/detail/11.1929.V.20160405.1702.006.html