飞机大迎角非定常气动力建模研究进展
2016-11-14汪清钱炜祺丁娣
汪清, 钱炜祺, 丁娣
1.中国空气动力研究与发展中心 空气动力国家重点实验室, 绵阳 621000 2.中国空气动力研究与发展中心 计算空气动力研究所, 绵阳 621000
飞机大迎角非定常气动力建模研究进展
汪清1,2,*, 钱炜祺1,2, 丁娣1,2
1.中国空气动力研究与发展中心 空气动力国家重点实验室, 绵阳621000 2.中国空气动力研究与发展中心 计算空气动力研究所, 绵阳621000
准确建立非定常气动力数学模型,是飞机大迎角飞行控制律设计、飞行动力学分析和飞行仿真的基础与前提。鉴于此,对大迎角非定常气动力建模研究进展,包括数学建模方法和人工智能建模方法两类进行了系统综述。其中:数学类建模方法是以对非定常流动现象和机理认识为基础的,主要有气动导数模型、非线性阶跃响应模型、状态空间模型、微分方程模型、非线性阶跃响应与状态空间混合模型以及迎角速率模型等;人工智能方法回避了复杂流动机理,属于黑箱非线性系统建模,主要有神经网络模型、模糊逻辑模型和支持向量机模型等。对于每种气动力模型,阐述了其建模思路和方法,给出了典型应用情况,并对其特点和局限性作了简要评述。最后,指出了当前大迎角非定常气动力建模研究工作存在的问题和未来研究方向。
大迎角; 失速/过失速; 非定常气动力; 气动力模型; 风洞试验; 飞行试验
近十几年来,大迎角非定常气动力问题越来越受到航空界的关注。对于军机而言,以F-22、F-35和T-50为代表的新一代战斗机设计均将过失速机动性能作为一项重要的战技指标,通过过失速机动来获取近距空战优势,提高作战效能;对于民机而言,虽然力图避免大迎角飞行,但由于恶劣的气象条件或操纵失误等因素导致飞机进入失速/过失速状态,进而出现失控的飞行事故时有发生,威胁着航空安全。飞机作失速/过失速飞行时,绕流流场十分复杂,气动力具有很强的非线性和非定常特征,常规的由静态气动力、动导数和旋转天平数据构成的气动力数据库,已不能满足失速/过失速飞行仿真和控制的需要,必须建立包含动态气动特性的失速/过失速飞行气动力数据库。
目前,地面试验是研究和预测飞机动态气动特性的主要手段。风洞动态试验与常规试验(静态试验、动导数试验和旋转天平试验等)有着本质的区别,这不仅体现在试验技术本身上,更体现在风洞试验与飞行动力学研究的关系方面,即风洞试验数据如何用于飞行控制系统设计、动力学分析和飞行仿真等飞行动力学问题的研究;飞行动力学问题的研究需要怎样的风洞试验数据。众所周知,静态气动力、动导数和锥运动气动力等常规气动力特性,都是马赫数、迎角、侧滑角和旋转角速度等飞行状态参数的函数,其数据库可以比较容易地通过一定量的风洞试验来建立。而大迎角动态气动力不仅取决于瞬时飞行状态,而且与运动历程密切相关,是运动历程的非线性泛函。因此,对于大迎角动态气动力,难以简单地像常规气动力那样,通过有限次数的风洞试验建立数据库,然后通过数据插值获得机动过程中任意时刻的气动力特性。一种现实可行的方法是,通过一定量的动态风洞试验,建立气动力数学模型,利用数学模型预测飞行过程中任意时刻的气动力特性。
非定常气动力建模问题正成为空气动力学、飞行力学和飞行控制领域共同关注的研究课题。已有的非定常气动力模型大致可以分为两类,一类是数学模型,包括气动导数模型、阶跃响应模型、状态空间模型和微分方程模型等;另一类是人工智能类模型,包括神经网络模型、模糊逻辑模型和支持向量机模型等。本文对国内外在大迎角非定常气动力建模方面的研究进展情况作一系统的回顾和简要的评述。
1 气动导数模型
1.1经典气动导数模型
早在1903年,Bryan和Williams就提出了纵向运动稳定导数模型[1]。稳定导数模型实际上是一种准定常模型,气动力和力矩仅依赖于飞机位移速度(u,v,w)和角速度(p,q,r)的瞬时值。此线性化模型没有考虑非定常效应,因此与运动的时间历程无关。
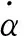
一个更严谨的方法[2]是,假设迎角的时间历程可以展开为收敛的Taylor级数,在时刻t,俯仰力矩系数对迎角的依赖性可以表示为
(1)

再对右端函数进行Taylor展开,作适当截断就得到线性稳定导数表达式:
(2)
式中:Cm0为零迎角俯仰力矩系数;Cm α为俯仰力矩系数对迎角α的导数。气动导数模型的物理意义清晰,在常规迎角范围内被广泛使用,但不适用于流动发生分离的大迎角情况。
1.2广义气动导数模型
经典的气动导数模型都是基于定常或准定常假设的,气动导数为常数。风洞试验研究表明[3-4],大迎角气动导数强烈地依赖于振动频率。为了描述气动导数对频率的依赖性,Lin和Lan[5]将多项式模型的模型系数视为减缩频率的函数,从而给出了一种广义的气动导数模型。
以俯仰振荡为例,将气动力系数表达为飞行状态变量及其变化率的函数:
Ci=c0+c1α+c2α2+c3α|α|+c4α3+
(3)
式中:Ci=CA,CN,Cm(CA为轴向力系数,CN为法向力系数);系数ci为减缩频率k的函数,其中,仅与α相关的系数可表达为
ci=ai0+ai1k+ai2k2+ai3k3
(4a)
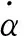
ci=ai0lg k+ai1k+ai2k2+ai3k3
(4b)
其中,对数函数用于描述小k值时,系数随k的快速变化,k值的下界限制为10-6。系数aij采用最小二乘法由试验数据拟合得到。
气动力模型式(3)和式(4)是针对谐波振动运动来建立的。对于一般的动态运动,需要等效成谐波振动,等效参数由下式确定:
(5)
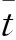
上述广义气动导数模型具有非常简洁的形式,模型系数具有类似于稳定导数的物理意义。但有两个值得思考的问题:其一,对于单自由度的俯仰振荡运动,每个气动系数模型中包含有36个未知参数,如果扩展到多自由度,待辨识的模型参数将非常庞大;其二,“等效”的概念是否成立。由于等效减缩频率值取决于瞬时迎角和迎角速率,因此式(3)的气动系数实际上也只与瞬时迎角和迎角速率有关,而与运动历程无关。
2 非线性阶跃响应模型
2.1原始非线性阶跃响应模型
Tobak[6]于1954年建立了线性非定常气动力的阶跃响应模型。其后,又与其合作者[7-12]利用Volterra原始泛函概念[13]将阶跃响应方法拓展到非线性领域,推导给出了阶跃响应形式的非线性非定常气动力模型。
以纵向平面运动的俯仰力矩系数为例,俯仰力矩系数Cm是迎角α、俯仰角速率q和升降舵偏角δe等飞行状态变量的函数。将飞行状态变量的时间历程分成一系列阶跃之和,如图1所示。
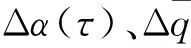
Cm(t)=Cm(-∞)+
(6)

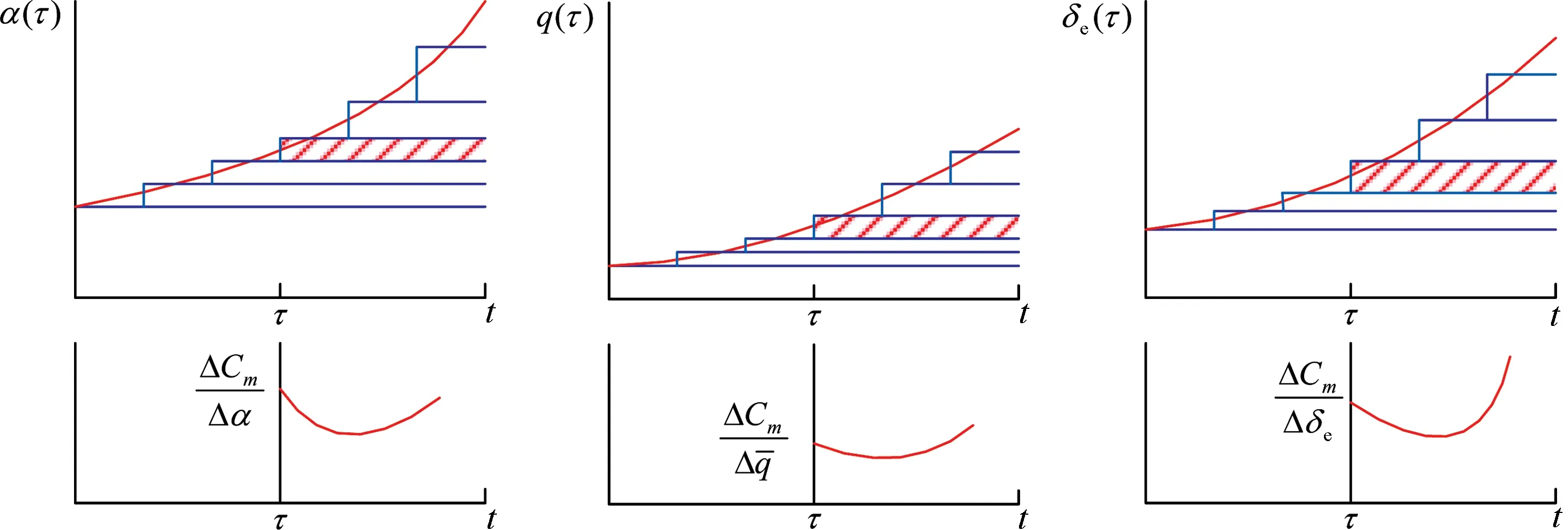
图1 阶跃响应之和[11]Fig.1 Summation of indicial responses[11]
Tobak的非线性阶跃响应模型在理论上是较完备的,围绕此模型开展的研究工作也是最广泛的。但由于模型结构过于复杂,通常情况下是不可辨识的,因此必须根据物理现象和机理作必要的简化。
2.2简化非线性阶跃响应模型
式(6)中的气动导数与时间历程α(ξ)、q(ξ)和δe(ξ)有关,其泛关系难以表达。因此,在实际应用时,需将其在ξ=τ处进行Taylor展开。对于飞机快速机动情况,取至展开式的一阶导数项,得到如下气动力模型:
Cm(t)=Cm(-∞)+
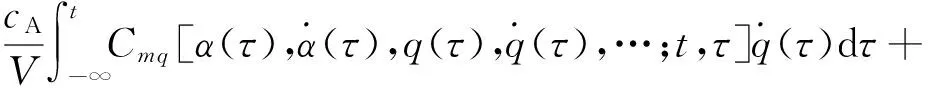
(7)
Cm(t)=Cm(-∞)+
(8)
对于模型式(8),将阶跃响应表示为平衡值与剩余函数之和,可得另一种形式的表达式:
Cm(t)=Cm[α(t),q(t),δe(t);∞]+
(9)
式中:第1项是定常气动力系数;后3项为非定常效应。
当气动力出现分叉点时,文献[11,14-15]提出在分叉点处采用差分公式,而在其余区域仍沿用上述积分形式的表达式。
上述简化非线性阶跃响应模型仍然十分复杂,在实际应用中还需要针对具体问题作进一步的简化。
此外,非定常气动力降阶模型[16-18]是非线性阶跃响应模型的另一种简化形式,其表达式为
Cm(t)=Cm0(Ma)+
(10)
式中:Ma为马赫数。式(10)中的阶跃响应函数可以通过解析法、风洞试验或计算流体力学(CFD)方法进行估计。目前解析法仅限于不可压无黏二维翼型[16],风洞试验方法尚未应用于阶跃响应函数估计,而CFD方法已用于确定给定构型的阶跃响应函数[17-18]。
2.3非线性阶跃响应模型的应用
Gupta和Iliff[19-20]在分析高性能战斗机F-15的3/8无动力遥控模型过失速和尾旋进入飞行试验数据时发现,当迎角α<40° 时,非定常效应不明显,可用二次多项式描述法向力系数CN和俯仰力矩系数Cm;而当迎角α>40° 时,非定常效应十分显著,多项式模型不再适用,如图2所示[20]。于是,采用简化的非线性阶跃响应模型描述大迎角区域的法向力和俯仰力矩系数,获得了与飞行试验数据符合较好的结果。所作的简化是,忽略飞行状态对阶跃响应的影响,即将非定常效应看做是线性的,并用阶梯函数来近似剩余函数。
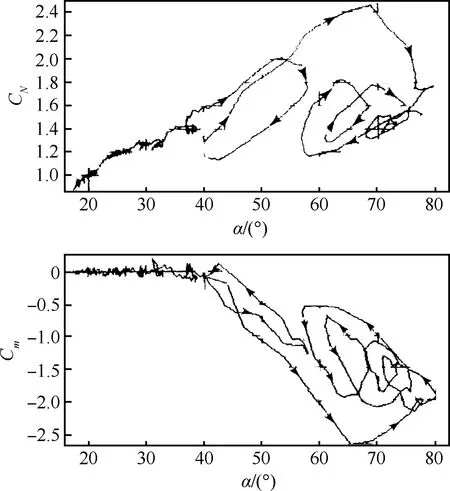
图2 F-15无动力遥控模型非定常气动力辨识结果[20]Fig.2 Estimated unsteady aerodynamics of unpowered telemeter-controlled model of F-15[20]
Klein等[21-27]也对非线性阶跃响应模型进行了简化,简化的气动力模型由静态项、纯旋转项和非定常项构成。并用简化模型分析处理了战斗机构型(F/A-18 HARV,F-16XL,X-31A)的风洞试验和飞行试验数据,建立其非定常气动力模型。
Reisenthel等[28-32]通过对阶跃函数空间进行二维参数化,发展了用于单自由度运动气动力预测的非线性阶跃响应模型,只需有限次数的阶跃响应试验,即可准确预测大迎角机动的非定常气动载荷。
3 状态空间模型
3.1Goman的状态空间模型
在大迎角下,分离流流场的动态发展过程产生非定常空气动力特性。Goman等[33-35]认为,可以适当选择一定数量的参数来描述分离流流场的关键特征,气动力响应取决于这些参数和瞬时飞行状态。
对于具有足够厚度的翼型,随迎角增大流动分离首先在后缘附近发生,气动力取决于迎角和分离点位置x[36]:
(11)
(12)
式中:CL为升力系数;分离点位置x∈[0,1],x=1表示完全附着流,x=0表示分离点位于前缘。在试验数据分析的基础上,Goman采用下列微分方程描述翼型分离点的动态特性:
(13)
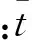
对于有涡破裂的俯仰三角翼绕流,Lan和Hsu[37]应用吸力模拟(Suction Analogy)方法给出了气动力的近似公式:
CL(α,x)=kpsin α cos2α+x2kvsin2α cos α
(14)
CD(α,x)=kpsin2α cos α+x2kvsin3α
(15)
Cm(α,x)=kpxpsin α cos α+x3kvxvsin2α
(16)
式中:CD为阻力系数;第1项对应于未分离流;第2项为涡附加项;常数kp和kv仅依赖于机翼的几何特征,xp和xv分别为位流和涡流的压心坐标;x为机翼上涡破裂点的位置坐标。Goman等[33-35]用式(13)拟合了水洞试验结果[38],表明涡破裂点位置的动态特性也可以用式(13)近似描述,如图3所示。图中:红色实线为试验结果;蓝色虚线为预测结果。式(14)~式(16)与式(13)联立构成了三角翼大迎角纵向运动的气动力数学模型。

图3 三角翼涡破裂点位置[33]Fig.3 Vortex burst point location of a delta wing[33]
式(11)~式(12)和式(14)~式(16)均忽略了下洗迟滞、定常旋转等因素对气动载荷的影响。
Goman等[33-35]进一步将翼型和三角翼的大迎角非定常气动力数学模型形式推广到全机构形,并用线性近似计及下洗迟滞、定常旋转和控制面偏转等因素的影响,给出了飞机纵向平面运动的气动力数学模型:
(17)
(18)
(19)

CL nl(α,x)=CL1(α)g(x)+CL0(α)(1-g(x))
(20)
Cm nl(α,x)=Cm1(α)g(x)+Cm0(α)(1-g(x))
(21)
式中:CL1(α)、Cm1(α)和CL0(α)、Cm0(α)分别为非线性气动力系数CL nl和Cm nl在两个极限情况x=1和x=0下对迎角α的依赖关系。正则函数g(x)起着权函数的作用,g(x)∈[0,1]。
Goman模型是建立在物理机理基础上的,其核心是引入内在状态变量描述流动结构,模型形式简洁,易于扩展到多自由度情况。但由于模型关于待辨识的未知参数τ1、τ2与未知函数x0(α)、g(x)、CL1(α)、CL0(α)、Cm1(α)和Cm0(α)是强非线性的,要从动态风洞试验数据辨识这些未知参数和函数是十分困难的。
3.2对状态空间模型的发展
为了描述静态迟滞和临界状态,Abramov等[39-40]采用下列非线性微分方程代替式(19),来描述内在状态变量:
(22)
在静态迟滞存在两个稳定分支的情况下,非线性函数f采用三次多项式:
f(α*,x)=k0(α*)+k1(α*)x+
k2(α*)x2+k3(α*)x3
(23)

Fan和Lutze[41-42]对Goman状态空间模型作了两点发展,一是将静态依赖性x0(α)取为
(24)
二是将非线性函数CL(x,α,q)等展开为Taylor级数形式:
(25)
式中:
ai、bi和ci(i=1,2,…,5)为待定参数。表达式(25)类似于气动导数模型,只是这里的气动导数依赖于内在状态变量,从而依赖于流动结构。
对于横侧向气动特性,Lutze等[43]尝试了对各部件分别采用Goman模型建立气动力数学模型,然后进行迭加,得到全机的非定常气动力和力矩系数。当然这项工作还远不完善,有许多需要探讨的问题。
高正红和焦天峰[44-45]在Fan等的工作基础上对Goman模型作了进一步修正,即将式(19)中的时间常数τ1视做减缩频率的函数。并对NACA 005翼型常速率俯仰运动的三组试验数据进行了分析,用其中两组数据进行建模,然后预测第三组数据,认为修正后的模型显著改善了预测结果。对70° 三角翼动态风洞试验数据的分析,得到了类似的结论。文献[46]认为,这一修正“看来很奇特,没有物理意义”。
3.3状态空间模型的应用
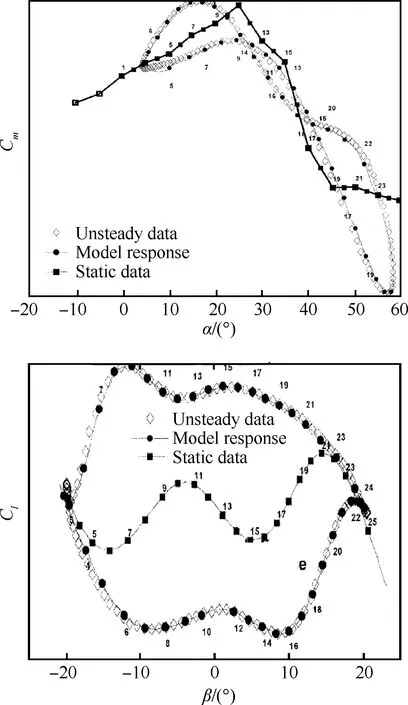
Goman等[33-35]采用他们自己提出的状态空间模型拟合了战斗机构形的大迎角自由振动风洞试验数据和大迎角机动飞行试验数据,表明微分方程模型能够较好地描述全机构形在大迎角下的非线性非定常空气动力特性。
德国国家航空航天研究院(DLR)的Fischenberg、Singh和Jategaonkar等用基本二维翼型模型成功辨识建立了VFW614、C-160和DO-328飞机的纵向和横侧向失速动力学模型[47-49]。在这些研究中,采用两参数双曲正切函数,而不直接辨识状态变量的静态非线性函数x0(α)。图4给出了DO-328失速迟滞特性建模结果与飞行试验数据的比较,其中实线为飞行试验数据,虚线为建模结果。横侧向的失速特性采用两个状态变量来描述,分别对应于左右机翼[50]。
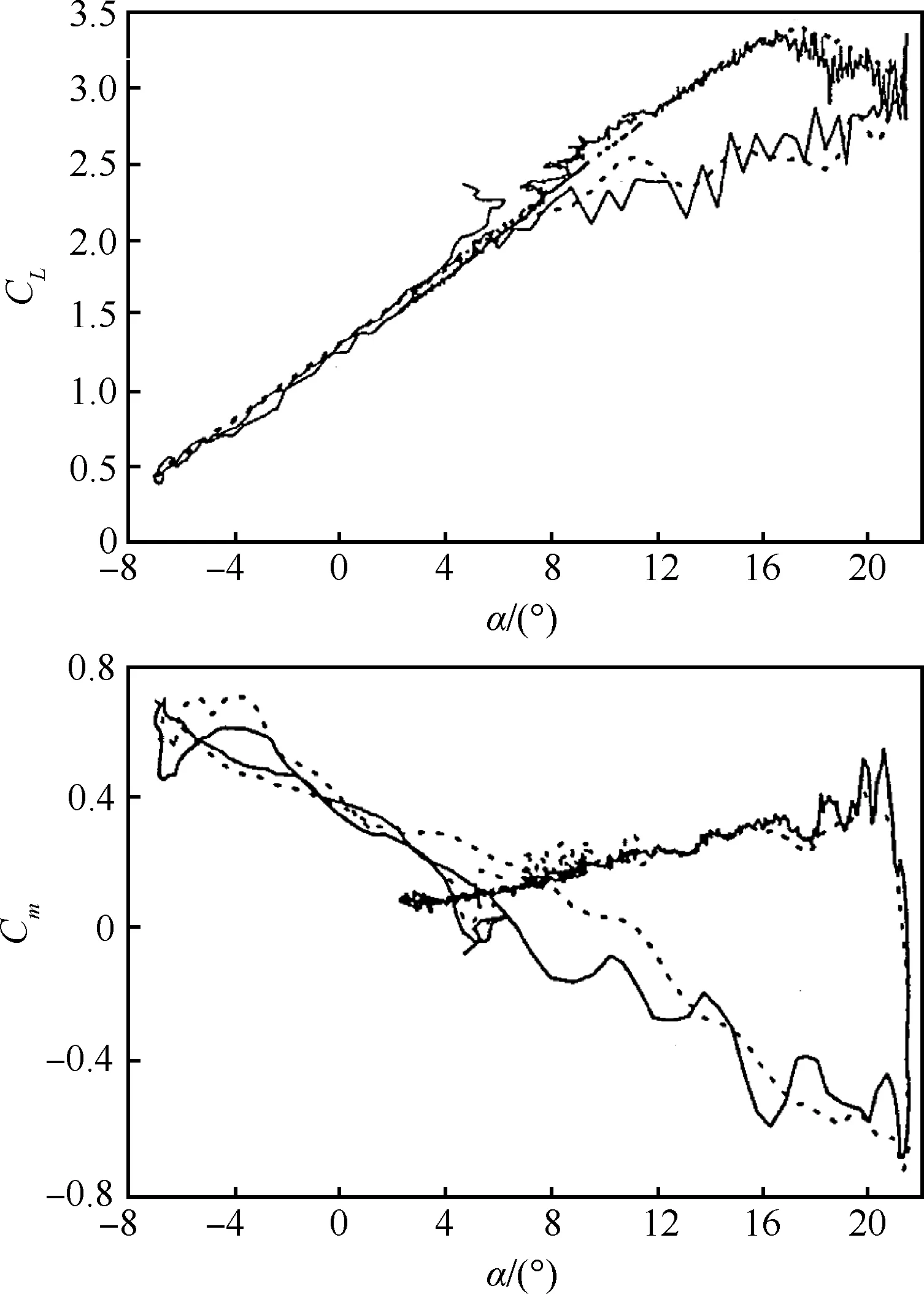
图4 Dornier 328失速迟滞特性建模[49]Fig.4 Modeling of stall hysteresis of Dornier 328[49]
Pashilkar和Pradeep[51]应用状态空间模型建立了F-16 法向力和俯仰力矩特性的数学模型。该项研究中,采用正交多项式表示未知函数,静态非线性函数x0(α)采用两参数双曲正切函数。
4 微分方程模型
4.1CARDC微分方程模型
中国空气动力研究与发展中心(CARDC)汪清等[52-55]采用增量法建模思路,将气动力分解为三部分:静态气动力、准定常气动力增量和非定常气动力增量。以俯仰运动为例,将气动力系数表达为
(26)
式中:Ci=CL,CD,Cm。
通过对大量风洞试验数据的分析,采用一阶微分方程描述由涡破裂和恢复迟滞引起的非定常气动力增量Ci unst:
(27)
式中:τ1为反映迟滞效应的时间常数。式(27)表明,气动力的过渡过程近似为指数律收敛过程。
式(26)和式(27)联立构成了飞机大迎角非定常气动力的微分方程模型。
此模型亦可由Tobak的非线性阶跃响应模型简化得到,因此具有其理论基础。特别值得一提的是,Klein等[21-27]提出的简化阶跃响应模型与此模型不谋而合!
笔者团队还用F-18、J-7II和翼身组合体等大振幅强迫振动风洞试验数据、战斗机模型自由振动风洞试验数据和飞行试验数据等对所发展的模型进行了检验,表明模型能够较好地描述大迎角气动力的非线性和非定常特性。图5给出了某型教练机缩比模型飞行试验法向力系数辨识结果与微分方程模型预测结果的比较[55]。
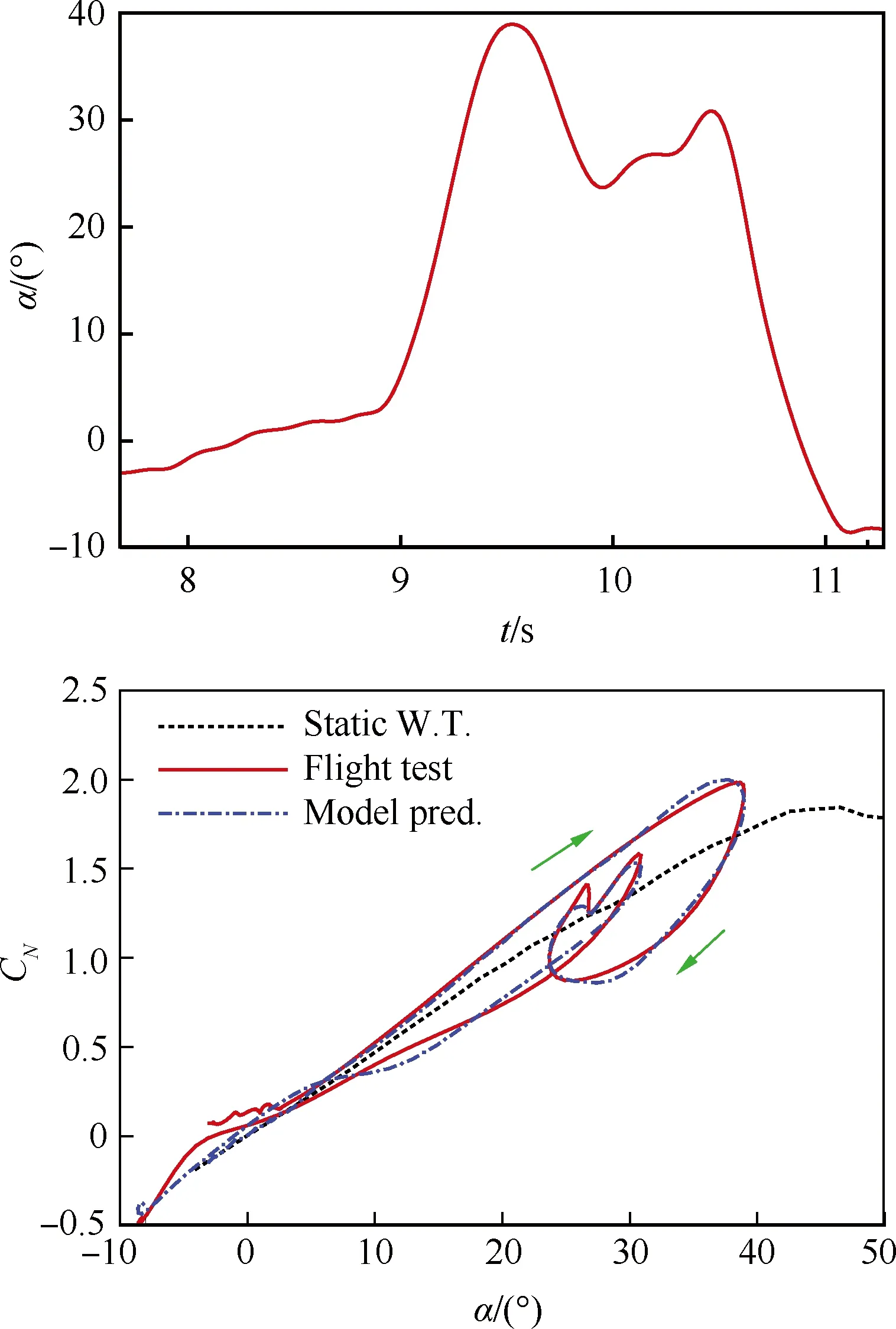
图5 某型教练机非定常气动力建模[55]Fig.5 Unsteady aerodynamic modeling of a training aircraft[55]
近年来,还将上述微分方程模型拓展到一般空间机动,提出了多自由度大迎角非定常气动力模型的结构形式[56],并用F18、F-16XL和SDM标模等构型的动态风洞试验数据对模型进行了初步验证。在此基础上,利用俯仰、偏航、滚转以及耦合运动动态风洞试验数据,建立了某型飞机的过失速机动非定常气动力数学模型。
对于多自由度情况,上述微分方程模型存在待辨识参数较多的问题。此外,特征时间常数τ1是α的非线性函数,辨识中必须保证τ1(α)>0。
4.2Goman微分方程模型
近年来,Goman在非定常气动力建模方面逐渐倾向于直接用微分方程描述气动力,而不再使用内在状态变量。Goman线性微分方程模型的形式为[39,40,57]
(28)
(29)
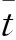
线性模型适用于小振幅且无静态迟滞的情况。当振幅增大或出现静态迟滞时,Goman等引入了下列非线性微分方程模型[57]:
(30)
采用此微分方程模型,避免了内在状态变量辨识所遇到的困难。
文献[39,40,57]针对简单的65° 三角翼,利用动态风洞试验数据建立了非定常气动力微分方程模型。但对于复杂的全机构型,Goman微分方程模型的描述能力尚未得到充分验证。此外,与CARDC微分方程模型类似,Goman微分方程模型也存在两方面局限性:一是对于多自由度情况待辨识参数较多;二是辨识中必须保证τ1(α)>0。
5 Fourier泛函分析
文献[58-59]基于Fourier泛函分析发展了一种大振幅强迫振动试验数据的分析方法,用不同频率下谐波运动的气动力响应建立升力、阻力和俯仰力矩系数的数学模型。
运用Fourier泛函分析方法,将一个周期内的谐波振荡器动力响应表示为
Cm=a0+(a1-ib1)eikτ+(a2-ib2)ei2kτ+
(a3-ib3)ei3kτ+…
(31)
通过对式(31)进行连续Fourier变换分析,可以得到气动力响应模型:
(1-PD3)+…
(32)
(33)
Peskett[60]对上述Fourier泛函分析方法进行了详细的阐述。由于Fourier泛函分析方法的特殊性,它仅适用于从单自由度强迫振荡试验数据来建立非定常气动力模型。
文献[58]用二维和三维非定常空气动力理论结果以及70° 三角翼试验数据对建模方法和气动力模型进行了检验,表明用该建模方法从大振幅振动试验数据建立的气动力模型能够较好地拟合试验数据,并能预测谐波和线性上仰运动的气动力响应。文献[59]用F-18的30° 振幅和20° 振幅谐波振动以及常速率上仰和下俯运动的气动力响应风洞试验数据进行了进一步的验证。
在国内,南京航空航天大学黄达等[61]、中国空气动力研究与发展中心姜裕标和沈礼敏[62]、航天气动研究院赵磊[63]、西北工业大学杨小平和孙秀佳[64]采用文献[58-59]发展的Fourier泛函分析法进行动态风洞试验数据的分析处理,都取得了较满意的结果。
6 非线性阶跃响应与状态空间混合模型
近年来,加拿大IAR的Huang等[65-67]发展了非线性阶跃响应模型与Goman状态空间模型的一种混合模型,用于65° 三角翼滚转力矩响应的气动建模。在Huang的研究中,涡破裂点位置x不是采用Goman的一阶响应模型式(13),而是采用非线性阶跃响应模型。对于自由滚转机翼,t时刻的涡破裂点位置用下列叠加积分表示:
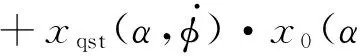
(34)
式中:x0为静态涡破裂点位置,由基于临界涡强度概念的半经验公式给出;xqst为准定常涡破裂点位置;阶跃响应函数xu从试验结果得出,其表达式为
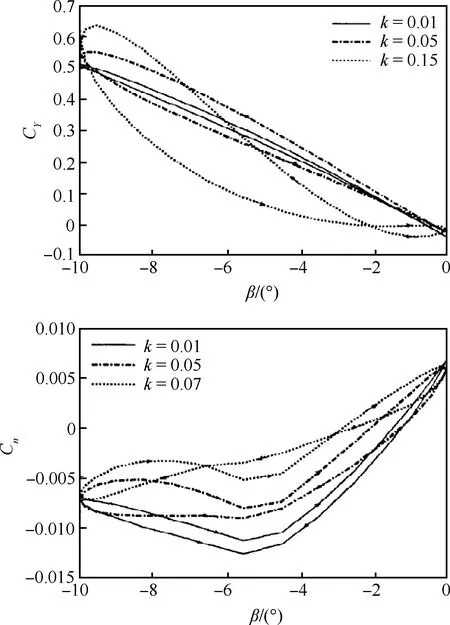
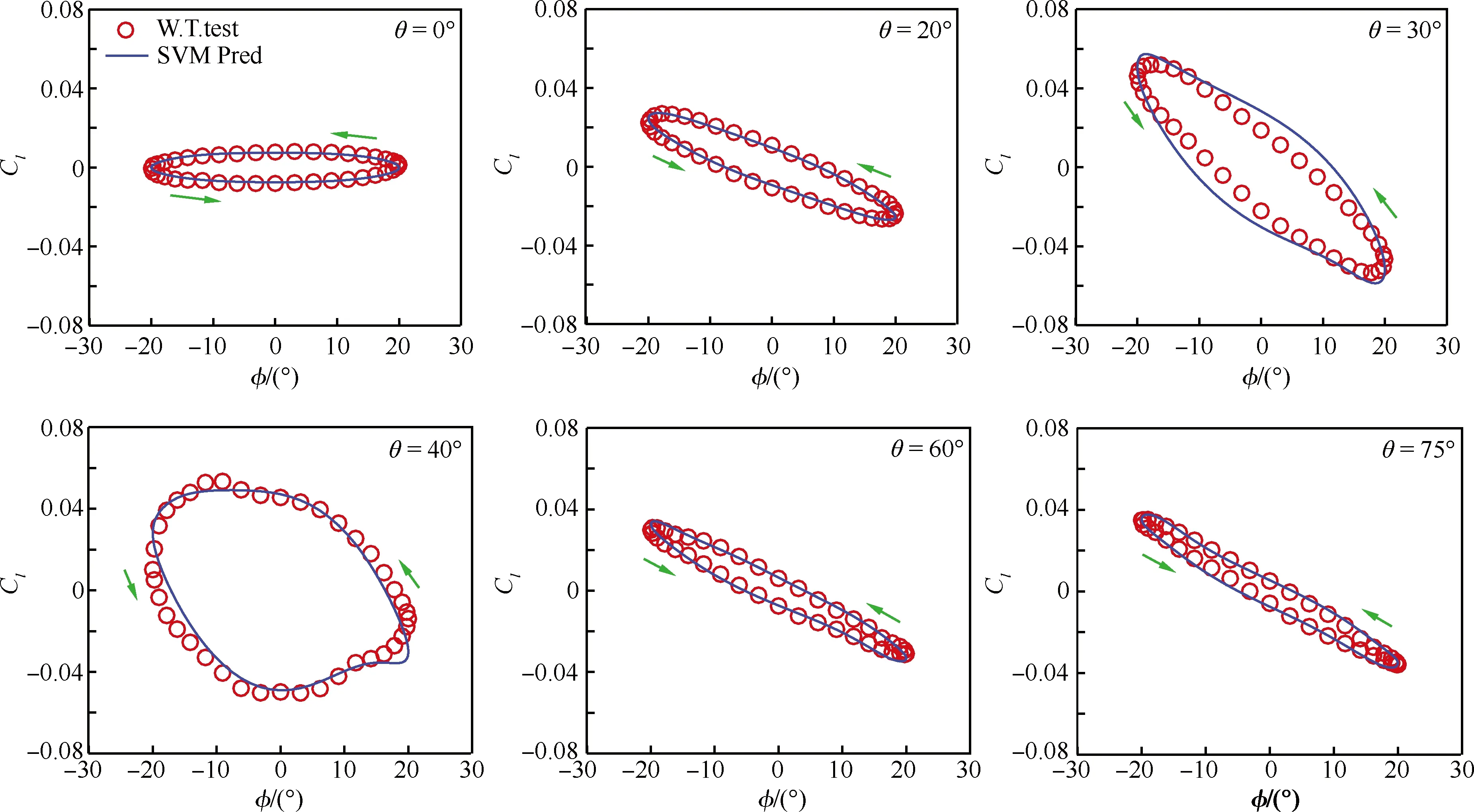
(35)
式中:T*为特征响应时间,阶跃响应截断到τ 目前,上述模型已得到65° 三角翼水洞试验结果的验证,但是否适用于复杂全机构型,还需要进一步验证。 近年来,印度国家航天实验室的Pashilkar[68-70]提出一种新的非定常气动力建模方法,称之为迎角速率模型。该模型的基本形式为 (36) 式中:f1为与速率相关的迎角位移函数;f2为与速率相关的法向力比例函数;α1为迟滞迎角;α*为位移f1得到的迎角。 位移迎角和迟滞迎角由下式表示: (37) (38) 迎角速率模型有两个显著特征:① 位移迎角被递归定义;② 迎角速率是迟滞的,而非迎角本身。在文献[69]所述模型辨识工作中,建议位移函数f1和比例函数f2正比于俯仰角速率,且在迎角增大和迎角减小的过程中取不同的值。图6给出了60° 三角翼俯仰振荡气动力建模结果与风洞试验数据的比较。 目前,上述模型已得到60° 三角翼风洞试验结果的验证,但是否适用于复杂全机构型,还需要进一步验证。此外,从模型结构形式来看,难以拓展到多自由度耦合运动。 图6 60° 三角翼非定常气动力建模[69]Fig.6 Unsteady aerodynamic modeling of a 60° delta wing[69] 神经网络因其强大的映射能力,在大迎角非定常气动力建模领域具有广阔的应用前景。Rokhsaz和Steck[71-72]在研究大迎角机动神经网络控制问题时,采用多层前馈网络来描述非线性非定常气动力。汪清等[55,73-74]也对大迎角非定常气动力的神经网络建模方法进行了研究,根据先验信息的利用程度发展了非定常气动力的三种神经网络模型。龚正和沈宏良[75]采用自适应神经网络建立非定常气动模型,其进步点是可以对网络结构进行自适应学习。 在函数逼近领域,早先最普遍采用的是BP网络,它是一种多层前馈神经网络,因网络训练采用误差反向传播(Back-Propagation, BP)学习算法而得名。近年来,随着径向基函数(Radial Basis Function, RBF)神经网络的提出和发展,为函数逼近提供了一种更有效的方法。RBF网络是一类三层前馈神经网络,其输入层由信号源节点组成;第二层为隐层,隐单元的个数由所描述的问题而定,隐层采用径向基函数作为网络的激励函数;第三层为输出层,采用线性激励函数。近期,汪清等[74]采用RBF神经网络建立某型飞机非定常气动力模型,获得了较满意的结果,模型对未参加建模状态的气动力预测结果与微分方程模型的一致性很好,如图7所示。 图7 某飞机两种非定常气动力模型预测结果的比较[74]Fig.7 Unsteady aerodynamics predicted by two kinds of aero models for an aircraft[74] 神经网络建模方法的困难在于如何确定最优模型结构。隐层神经元过少,不能充分拟合现有数据;隐层神经元过多,模型性能下降。尽管已有一些神经网络结构的自学习方法,但都不充分,只能确定较优的模型结构。 应用模糊逻辑算法进行系统辨识,不需要给出具体的函数关系式,因此适用于结构复杂而难以确知的多变量非线性系统。Wang等[76-77]首先应用模糊逻辑算法进行非线性非定常气动力的建模。在此工作基础上,Lan及其合作者应用模糊逻辑算法分析了部分军机[78-80]和民机[81-83]的飞行试验数据,建立其非定常气动力模型。 用模糊逻辑算法建立的模型没有具体的函数关系式,而是关于输入、输出变量的一个数据结构。模糊逻辑模型的基本元素为内部函数、隶属函数和输出单元。 (39) 式中:Ci=CA,CN,Cm(CA为轴向力系数)。假设所有气动系数关于侧滑角β是对称的。在静态情况下,减缩频率k等于零。 对于大振幅偏航和滚转振动试验,将非定常气动力系数表示为如下形式[77]: (40) 式中:Ci=CY,Cl,Cn(CY为横向力系数,Cl为滚转力矩系数,Cn为偏航力矩系数);φ为滚转角;ψ为偏航角。 采用模糊逻辑描述非线性依赖关系式(39)和式(34);采用Newton梯度法确定内部函数的系数;采用结构辨识算法确定最优模型结构。需要指出的是,模糊逻辑结构复杂性随输入变量的增加而成指数上升,过多的输入变量可能会使模型结构过于复杂而不可辨识。 特别值得关注的是,Lan及其合作者应用模糊逻辑算法分析处理了一些失事民机的黑匣子数据[82-83]。对于某型喷气式运输机,在利用飞行数据建立非定常气动模糊逻辑模型的基础上,分析了减缩频率对非定常气动特性的影响,如图8所示。 图8 减缩频率对某运输机非定常气动特性的影响[82]Fig.8 Reduced frequency effects on unsteady aerodynamics of a jet transport aircraft[82] 在国内,南京航空航天大学尹江辉和刘昶[84]、史志伟和吴根兴[85],中国空气动力研究与发展中心刘志涛等[86-87]、孔轶男等[88-89]也采用模糊逻辑建模方法开展了相关的研究。 支持向量机(Support Vector Machine, SVM)是机器学习领域发展的新工具,由Vapnik[90]于1995年提出。SVM最初用于模式识别,其后成功地扩展应用于函数拟合和非线性系统建模。SVM,采用结构风险最小化准则,代替了神经网络和模糊逻辑中的经验风险最小化准则,因此具有更好的泛化性能。 用于系统建模的SVM,称为SVM回归。它通过引入从输入空间Rm到特征空间F的非线性映射,将非线性系统建模问题转化为一个二次规划问题,其目标函数为凸函数,存在唯一极值点。但是标准SVM存在“维数灾难”问题,当样本数量较大时,训练算法过于复杂而难以实现。作为标准SVM的一个重要扩展,Suykens和Vandewalle[91]于1999年提出了最小二乘SVM (LS-SVM),将二次规划问题转变成线性方程组求解,大大简化了计算复杂性,在函数拟合和系统建模中得到广泛应用。 对于多输入-单输出(MIOS)非线性系统建模问题,SVM利用在高维特征空间F中的线性回归来拟合非线性函数: y=f(x)=wTφ(x)+bx∈Rm,y∈R (41) 式中:φ(x)为从输入空间Rm到特征空间F的非线性映射;w为权向量;b为偏置。 假设通过试验测量获得了有限样本数据集{(xi,yi),i=1,2,…,n}。采用结构风险最小化准则,LS-SVM优化目标和约束为 (42) 式中:ξi为松弛因子;c为给定的常数,用于控制训练误差与回归函数平滑度之间的折中。 引入Lagrange函数求解等式约束优化问题,并利用KKT条件可以将优化问题式(42)转化为线性系统求解问题,即 (43) 式中: (44) K(xi,xj)称为核函数,其值为向量xi和xj在特征空间的内积,即 K(xi,xj)=φ(xi)·φ(xj) 求解方程式(44)得到参数ai(i=1,2,…,n)和b后,LS-SVM模型即为 (45) 文献[92-93]应用LS-SVM方法开展了大迎角非定常气动力建模研究。其中文献[93]着重探讨了LS-SVM建模的三个方面问题:输入变量选择、输出变量选择和SVM参数确定,认为:① 可以用飞行状态的当前值及之前的若干个采样值作为输入,以描述运动历程对气动力的影响;② 为充分利用静态风洞试验数据精准度高的特点,建议在气动力分解的基础上仅对非定常气动力增量进行建模;③ 对于大迎角非定常气动力建模,采用径向基核函数是适当的,可以通过k-折交叉检验确定罚因子c和核宽度σ,但在对训练样本集进行k-折划分时,应将一个试验状态的全部数据作为一个整体,参与训练或检验。 文献[93]利用F-16XL滚转振荡风洞试验数据开展了LS-SVM建模方法的应用研究。图9给出了部分预测结果与试验数据的比较。 图9 F-16XL滚转力矩系数LS-SVM模型预测结果[93]Fig.9 Prediction of roll moment coefficient LS-SVM model for F-16XL[93] 首先利用α=0°~75°、振幅φs=10°,30°的试验数据建立Cl的LS-SVM模型,然后,将所建立的模型推广到振幅φs=20°的滚转振荡,预测滚转力矩系数响应。建模和预测结果表明,LS-SVM具有很强的学习能力和良好的泛化性能,是大迎角非定常气动力建模的一种极具吸引力和应用前景的方法。 LS-SVM建模方法的局限性在于,随着训练样本数n的增大,线性方程组式(43)求解的复杂性和计算时间迅速增加。例如,当n>104时,LS-SVM建模就已十分困难。 1) 数学类气动力模型易于为工程设计人员所接受,是大迎角非定常气动力建模研究的主要发展方向。 2) 在数学类非定常气动力模型中,非线性阶跃响应模型和微分方程模型最具工程应用前景,前者的理论基础较完备,后者具有较清晰的物理意义,能够较好地与经典的小迎角气动导数模型相衔接。 3) 随着人工智能的迅速发展,让计算机通过对一定量的静态和动态风洞试验数据的学习,来预测飞机在机动飞行中的气动力响应,是完全可能的。因此,人工智能类非定常气动力建模方法,是一个值得关注的研究方向。 4) 从公开文献来看,大迎角非定常气动力建模研究工作仍处于学术研究阶段,距离工程应用还有一定差距。其中一个重要原因是,目前的研究工作大多是针对单自由度俯仰或滚转运动开展的。未来研究工作应向多自由度耦合的空间机动拓展。 5) 无论数学类或人工智能类气动力建模,都需要以风洞试验数据为支撑,试验数据的完备性在很大程度上决定了所建立的气动力模型的适用范围。因此,在开展建模方法研究的同时,还应当重视面向气动力建模的风洞试验设计问题。 [1]ABZUG M J. Airplane stability and control[M]. Cambridge: Cambridge University Press, 1977: 108-121. [2]ETKIN B, REID L D. Dynamics of atmospheric flight: stability and control[M]. New York: John Wiley & Sons Inc, 1972: 264-293. [3]BRANDON J M, FOSTER J V. Recent dynamic measurements and considerations for aerodynamic modeling of fighter airplane configurations: AIAA-1998-4447[R]. Reston: AIAA, 1998. [4]GREENWELL D I. Frequency effects on dynamic stability derivatives obtained from small-amplitude oscillatory testing[J]. Journal of Aircraft, 1998, 35(5): 776-783. [5]LIN G F, LAN C E. A generalized dynamic aerodynamic coefficient model for flight dynamics applications: AIAA-1997-3643[R]. Reston: AIAA, 1997. [6]TOBAK M. On the use of the indicial function concept in the analysis of unsteady motion of wings and wing-tail combinations: NACA R-1188[R]. Washington, D.C.: NACA, 1954. [7]TOBAK M, PEARSON W E. A study of nonlinear longitudinal dynamic stability: NASA TR R-209[R]. Washington, D.C.: NASA, 1964. [8]TOBAK M. On nonlinear longitudinal dynamic stability[G]. AGARD CP-17, Part 1, Neuilly Sur Seine: AGARD, 1966. [9]TOBAK M, SCHIFF L B. On the formulation of the aerodynamics in aircraft dynamics: NASA TR R-456[R]. Washington, D.C.: NASA, 1976. [10]SCHIFF L B, TOBAK M, MALCOLM G N. Mathematical modeling of the aerodynamics of high-angle-of-attack maneuvers: AIAA-1980-1583[R]. Reston: AIAA, 1980. [11]TOBAK M, SCHIFF L B. Aerodynamic mathematical modeling basic concepts[G]. AGARD LS-114, Lecture No.1, Neuilly Sur Seine: AGARD, 1981. [12]TOBAK M, CHAPMAN G T, SCHIFF L B. Mathematical modeling of the aerodynamic characteristics in flight dynamics: NASA TM-85880[R]. Washington, D.C.: NASA, 1984. [13]VOLTERRA V. Theory of functional and of integral and integro-differential equations[M]. New York: Dover Publications, Inc., 1959: 23-28. [14]TOBAK M, SCHIFF L B. The role of time-history effects in the formulation of the aerodynamics of aircraft dynamics[G]. AGARG CP-235, Paper No.26, Neuilly Sur Seine: AGARD, 1978. [15]TOBAK M, CHAPMAN G T, UNAL A. Modeling aerodynamic discontinuities and the onset of chaos in flight dynamical systems: NASA TM-89420[R]. Washington, D.C.: NASA, 1986. [16]SINGH R, BAEDER J. Direct calculation of three-dimensional indicial lift response using computational fluid dynamics[J]. Journal of Aircraft, 1997, 34(4): 465-471. [17]GHOREYSHI M, CUMMINGS R M, DaRonch A, et al. Transonic aerodynamic load modeling of X-31 aircraft pitching motions[J]. AIAA Journal, 2013, 51(10): 2447-2464. [18]GHOREYSHI M, JIRASEK A, CUMMINGS R M. Reduced order unsteady aerodynamic modeling for stability and control analysis using computational fluid dynamics[J]. Progress of Aerospace Science, 2014, 71: 167-217. [19]GUPTA N K, ILIFF K W. Identification of aerodynamic indicial functions using flight data: AIAA-1982-1375[R]. Reston: AIAA, 1982. [20]GUPTA N K, ILIFF K W. Identification of integro-differential system for application to unsteady aerodynamics and aeroelasticity: AIAA-1985-1763[R]. Reston: AIAA, 1985. [21]KLEIN V, NODERER K D. Modeling of aircraft unsteady aerodynamic characteristics, Part 1—postulated models: NASA TM-109120[R]. Washington, D.C.: NASA, 1994. [22]KLEIN V, NODERER K D. Modeling of aircraft unsteady aerodynamic characteristics, Part 2—parameter estimated from wind tunnel data: NASA TM-110161[R]. Washington, D.C.: NASA, 1995. [23]KLEIN V, NODERER K D. Modeling of aircraft unsteady aerodynamic characteristics, Part 3—Parameter estimated from flight data: NASA TM-110259[R]. Washington, D.C.: NASA, 1996. [24]KLEIN V, MURPHY P C, CURRY T J, et al. Analysis of wind tunnel longitudinal static and oscillatory data of the F-16XL aircraft: NASA TM-97-206276[R]. Washington, D.C.: NASA, 1997. [25]KLEIN V, MURPHY P C. Estimation of aircraft nonlinear unsteady parameters from wind tunnel data: NASA TM-1998-208969[R]. Washington, D.C.: NASA, 1998. [26]SMITH M S. Analysis of wind tunnel oscillatory data of the X-31A aircraft: NASA CR-1999-208725[R]. Washington, D.C.: NASA, 1999. [27]MURPHY P C, KLEIN V. Estimation of aircraft nonlinear unsteady parameters from dynamic wind tunnel testing: AIAA-2001-4016[R]. Reston: AIAA, 2001. [28]REISENTHEL P H. Development of a nonlinear indicial model for maneuvering fighter aircraft: AIAA-1996-0896[R]. Reston: AIAA, 1996. [29]REISENTHEL P H. Application of nonlinear indicial model to the prediction of a dynamically stalling wing: AIAA-1996-2493[R]. Reston: AIAA, 1996 [30]REISENTHEL P H, BETTENCOURT M T, MYATT J H, et al. A nonlinear indicial prediction tool for unsteady aerodynamic modeling: AIAA-1998-4350[R]. Reston: AIAA, 1998. [31]REISENTHEL P H, BETTENCOURT M T. Data-based aerodynamic modeling using nonlinear indicial theory: AIAA-1999-0763[R]. Reston: AIAA, 1999. [32]REISENTHEL P H, BETTENCOURT M T. Extraction of nonlinear indicial and critical state responses from experimental data: AIAA-1999-0764[R]. Reston: AIAA, 1999. [33]Гоман, М Г, Столяров Г И, Тартышников С Л, et al. Описание продольных аэродинамичес характеристик самолета гольших углах атак с учтом динамических зффектов отривного обтекания[C]//Издательский Отдел ЦАГИ, Препринт No.9. Москва: ЦАГИ, 1990. GOMAN M G, KHRABROV A N, STOLYAROV G I, et al. Mathematical description of longitudinal aerodynamic characteristics of an aircraft at high angles of attack with accounting for dynamic effects of separated flow[C]//Preprint of TsAGI, No.9. Moscow: TsAGI, 1990 (in Russian). [34]GOMAN M, KHRABROV A. State-space representation of aerodynamic characteristics of an aircraft at high angles of attack: AIAA-1992-4651[R]. Reston: AIAA, 1992. [35]GOMAN M G, KHRABROV A N, USOLTSEV S P. Unsteady aerodynamic model for large amplitude maneuvers and its parameter identification[C]//The International Federation of Automatic Control, 11th IFAC Symposium on System Identification. Kitakyushu: IFAC, 1997: 399-404. [36]Гоман, М Г. Математическое Описамие Азродинамических и Моментов на Неустановившихся Режимах Обтекания Неединственной Структурой[C]//Труды ЦАГИ, Выпуск 2195. Москва: ЦАГИ, 1983. GOMAN M G. Mathematical description of aerodynamic forces and moments at nonstationary flow regimes with a nonunique structure[C]//Proceedings of TsAGI, Issue 2195. Moscow: TsAGI, 1983 (in Russian). [37]LAN C E, HSU C H. Effects of vortex breakdown on longitudinal and lateral-directional aerodynamics of slender wings by the suction analogy: AIAA-1982-1385[R]. Reston: AIAA, 1982. [38]Головкин М А, Горбань В П, Ефремов А А, Симусева Е В. Гистереэисные Явления в Положении Областей Взрыва Вихрей при Нестционарных Движениях Треугольного Крыла[C]//Труды ЦАГИ, Выпуск 2319. Москва: ЦАГИ, 1986. GOLOVKIN M A, GORBAN V P, YEFREMOV A A, et al. Hysteretic phenomena in vortex burst region position at nonstationary delta wing motions[C]//Proceedings of TsAGI, Issue 2319. Moscow: TsAGI, 1986 (in Russian). [39]ABRAMOV N B, GOMAN M G, KHRABROV A N, et al. Simple wings unsteady aerodynamics at high angles of attack—experimental and modeling results: AIAA-1999-4013[R]. Reston: AIAA, 1999. [40]ABRAMOV N B, GOMAN M G, GREENWELL D I, et al. Two-step linear regression method for identification of high incidence unsteady model: AIAA-2001-4080[R]. Reston: AIAA, 2001. [41]FAN Y G, LUTZE F H. Identification of an unsteady aerodynamic model at high angles of attack: AIAA-1996-3407[R]. Reston: AIAA, 1996. [42]FAN Y G. Identification of an unsteady aerodynamic model up to high angle of attack regime[D]. Blacksburg, VA: Virginia Polytechnic Institute and State University, 1997. [43]LUTZE F H, FAN Y G, STAGG G. Multiaxis Unsteady Aerodynamic Characteristics of an Aircraft: AIAA-1999-4011[R]. Reston: AIAA, 1999. [44]高正红, 焦天峰. 飞行器快速俯仰产生大迎角非定常气动力数学模型研究[J]. 西北工业大学学报, 2001, 19(4): 506-510. GAO Z H, JIAO T F. On an unsteady aerodynamics model for pitching-oscillating body at high angle of attack[J]. Journal of Northwestern Polytechnical University, 2001, 19(4): 506-510 (in Chinese). [45]JIAO T F, GAO Z H. Unsteady aerodynamic modeling at high angles of attack: AIAA-2000-3908[R]. Reston: AIAA, 2000. [46]GREENWELL D I. A review of unsteady aerodynamic modeling for flight dynamics of maneuverable aircraft. AIAA-2004-5276[R]. Reston: AIAA, 2004. [47]FISCHENBERG D. Identification of an unsteady aerodynamic stall model from flight test data: AIAA-1995-3438[R]. Reston: AIAA, 1995. [48]SINGH J, JATEGAONKAR R V. Flight determination of configurational effects on aircraft stall behavior: AIAA-1996-3441[R]. Reston: AIAA, 1996. [49]JATEGAONKAR R V, MONNICH W. Identification of DO-328 aerodynamic database for a Level D flight simulator: AIAA-1997-3729[R]. Reston: AIAA, 1997. [50]SINGH J, JATEGAONKAR R V. Identification of lateral-direction behavior in stall from flight data[J]. Journal of Aircraft, 1996, 33(3): 627-630. [51]PASHILKAR A A, PRADEEP S. Unsteady aerodynamic modeling using multivariate orthogonal polynomials: AIAA-1999-4014[R]. Reston: AIAA, 1999. [52]汪清, 蔡金狮. 飞机大迎角非定常气动力建模与辨识[J]. 航空学报, 1996, 17(4): 391-398. WANG Q, CAI J S. Unsteady aerodynamic modeling and identification of airplane at high angles of attack[J]. Acta Aeronautica et Astronautica Sinica, 1996, 17(4): 391-398 (in Chinese). [53]CAI J S, WANG Q. Nonlinear unsteady aerodynamic mathematical models for aircraft[C]//Proceedings of the First Asian Computational Fluid Dynamics Conference. Hong Kong: The Hong Kong University, 1995: 273-280. [54]HE K F, WANG Q, CAI J S. Unsteady aerodynamic models at high angles-of-attack and their application to numerical simulation of post stall maneuvers[C]//Proceedings of the 6th Sino-Russian Symposium on Aerodynamics. Moscow: TsAGI, 1997: 146-157. [55]汪清. 飞机大迎角非定常气动力建模及其应用研究[D]. 西安: 西北工业大学, 1994. WANG Q. Unsteady aerodynamic modeling of aircraft at high angles of attack and its applications[D]. Xi’an: Northwestern Polytechnical University, 1994 (in Chinese). [56]汪清, 何开锋, 钱炜祺, 等. 飞机大迎角空间机动气动力建模研究[J]. 航空学报, 2004, 25(5): 447-451. WANG Q, HE K F, QIAN W Q, et al. Aerodynamic modeling of spatial maneuvering aircraft at high angle of attack[J]. Acta Aeronautica et Astronautica Sinica, 2004, 25(5): 447-451 (in Chinese). [57]ABRAMOV N B, GOMAN M G, KHRABROV A N. Aircraft dynamics at high incidence flight with account of unsteady aerodynamic effects: AIAA-2004-5274[R]. Reston: AIAA, 2004. [58]CHIN S, LAN C E. Fourier functional analysis for unsteady aerodynamic modeling[J]. AIAA Journal, 1992, 30(9): 2259-2266. [59]HU C C, LAN C E, BRANDON J. Unsteady aerodynamic modeling for maneuvering aircraft: AIAA-1993-3626[R]. Reston: AIAA, 1993. [60]PESKETT J P. The development of unsteady aerodynamic mathematical models[D]. Bristol: University of Bristol, 1998. [61]黄达, 李志强, 吴根兴. 大振幅非定常实验数学模型与动导数仿真实验. 空气动力学学报, 1999, 17(2): 219-223. HUANG D, LI Z Q, WU G X. Dynamic derivative simulation and mathematical model of the wind tunnel test about a model pitching in very large amplitude[J]. Acta Aerodynamica Sinica, 1999, 17(2): 219-223 (in Chinese). [62]姜裕标, 沈礼敏. 非定常气动力试验与建模研究[J]. 流体力学实验与测量, 2000, 14(4): 26-31. JIANG Y B, SHEN L M. An experimental investigation on unsteady aerodynamics and modeling for a fighter configuration[J]. Experiments and Measurements In Fluid Mechanics, 2000, 14(4): 26-31 (in Chinese). [63]赵磊. 大迎角气动力预示方法研究[D]. 北京: 北京空气动力研究所, 1997. ZHAO L. Prediction methods of aerodynamics at high angles of attack[D]. Beijing: Beijing Aerodynamics Institute, 1997 (in Chinese). [64]杨小平, 孙秀佳. 飞机大迎角机动非线性气动力模型的辨识[J]. 飞行力学, 1998, 16(1): 37-42. YANG X P, SUN X J. Identification of nonlinear aerodynamic model for maneuvering aircraft at high angle of attack[J]. Flight Dynamics, 1998, 16(1): 37-42 (in Chinese). [65]HUANG X Z, LOU H Y, HANFF E S. Nonlinear indicial response and internal state-space representation for free-to-roll trajectory prediction of 65° delta wing at high incidence: AIAA-2002-4713[R]. Reston: AIAA, 2002. [66]HUANG X Z, HANFF E S. Hysteresis and bifurcation analysis of a fighter and a delta wing at high incidence: AIAA-2002-4714[R]. Reston: AIAA, 2002. [67]HUANG X Z. Nonlinear indicial response/internal state-space representation and its application on delta wing aerodynamics: AIAA-2003-3944[R]. Reston: AIAA, 2003. [68]PASHILKAR A A. Unsteady aerodynamic modeling at high incidence for flight dynamic analysis: AIAA-2001-4079[R]. Reston: AIAA, 2001. [69]PASHILKAR A A. Flow incidence rate model for unsteady aerodynamics at high angles of attack: AIAA-2001-2469[R]. Reston: AIAA, 2001. [70]PASHILKAR A A. Flight dynamic analysis of the flow incidence rate model: AIAA-2002-0098[R]. Reston: AIAA, 2002. [71]ROKHSAZ K, STECK J E. Use of neural network in control of high-alpha maneuvers[J]. Journal of Guidance, Control, and Dynamics, 1993, 16(5): 934-939. [72]ROKHSAZ K, STECK J E. Application of artificial neural networks in nonlinear aerodynamics and aircraft design[J]. Journal of Aerospace, 1993, 102: 1790-1798. [73]WANG Q, WU K Y, ZHANG T J, et al. Aerodynamic modeling and parameter estimation from the QAR data of an airplane approaching high-altitude airport[J]. Chinese Journal of Aeronautics, 2012, 25(3): 361-371. [74]WANG Q, HE K F, QIAN W Q, et al. Unsteady aerodynamics modeling for flight dynamics application[J]. Acta Mechanica Sinica, 2012, 28(1): 14-23. [75]龚正, 沈宏良. 非定常气动力的结构自适应神经网络建模方法[C]//中国航空学会第22届飞行力学与飞行试验学术交流会论文集. 北京: 中国航空学会, 2006: 67-71. GONG Z, SHEN H L. Unsteady aerodynamic modeling method using structural adaptive neural network[C]//Proceedings of the 22th Chinese Symposium on Flight Dynamics and Flight Tests. Beijing: Chinese Society of Aeronautics and Astronautics, 2006: 67-71 (in Chinese). [76]WANG Z, LAN C E, BRANDON J M. Fuzzy logic modeling of nonlinear unsteady aerodynamics: AIAA-1998-4351[R]. Reston: AIAA, 1998. [77]WANG Z, LAN C E, BRANDON J M. Fuzzy logic modeling of lateral-directional unsteady aerodynamics: AIAA-1999-4012[R]. Reston: AIAA, 1998. [78]WANG Z, LI J, LAN C E, et al. Estimation of unsteady aerodynamic models from flight test data: AIAA-2001-4017[R]. Reston: AIAA, 2001. [79]WANG Z, LAN C E, BRANDON J M. Estimation of lateral-directional unsteady aerodynamic models from flight test data: AIAA-2002-4626[R]. Reston: AIAA, 2002. [80]LAN C E, LI J, YAU W, et al. Longitudinal and lateral-directional coupling effects on nonlinear unsteady aerodynamic modeling from flight data: AIAA-2002-4804[R]. Reston: AIAA, 2002. [81]PAN C, LAN C E. Estimation and analysis of unsteady aerodynamic models of a jet transport by a fuzzy logic algorithm using flight-data-recorder data: AIAA-2002-4494[R]. Reston: AIAA, 2002. [82]WENG C T, HO C H, LAN C E. Aerodynamic model estimation and analysis for a jet transport in a landing accident: AIAA-2003-5699[R]. Reston: AIAA, 2003. [83]LI J, LAN C E. Unsteady aerodynamic modeling of aircraft response to atmospheric turbulence: AIAA-2001-4017[R]. Reston: AIAA, 2001. [84]尹江辉, 刘昶. 一种非定常气动力的模糊逻辑模型[C]//中国2000年飞行力学与飞行试验学术年会论文集. 北京: 中国航空学会, 2000: 222-229. YIN J H, LIU C. Fuzzy logic model of unsteady aerodynamics[C]//Proceedings of Chinese Symposium on Flight Dynamics and Flight Tests. Beijing: Chinese Society of Aeronautics and Astronautics, 2000: 222-229 (in Chinese). [85]史志伟, 吴根兴. 多变量非线性非定常气动力的模糊逻辑模型[J]. 空气动力学学报, 2001, 19(1): 103-108. SHI Z W, WU G X. Fuzzy logic model of nonlinear unsteady aerodynamics with multiple variables[J]. Acta Aerodynamica Sinica, 2001, 19(1): 103-108 (in Chinese). [86]刘志涛. 孙海生, 姜裕标, 等. 非线性非定常气动力的模糊逻辑建模方法[J]. 实验流体力学, 2005, 19(1): 99-103. LIU Z T, SUN H S, JIANG Y B, et al. Fuzzy logic modeling of nonlinear unsteady aerodynamics[J]. Journal of Experiments in Fluid Mechanics, 2005, 19(1): 99-103 (in Chinese). [87]刘志涛. 大迎角非定常气动力试验和建模研究[D]. 绵阳: 中国空气动力研究与发展中心, 2004. LIU Z T. Experiment and modeling of unsteady aerodynamics at high angles of attack[D]. Mianyang: China Aerodynamics Research and Development Center, 2004 (in Chinese). [88]孔轶男, 何开锋, 钱伟祺, 等. 非定常气动力建模的模糊逻辑方法[C]//飞行力学与飞行试验学术交流年会论文集. 北京: 中国航空学会, 2004: 82-86. KONG Y N, HE K F, QIAN W Q, et al. Fuzzy logic method for unsteady aerodynamic modeling[C]//Proceedings of Chinese Symposium on Flight Dynamics and Flight Tests. Beijing: Chinese Society of Aeronautics and Astronautics, 2004: 82-86 (in Chinese). [89]孔轶男. 气动力建模的模糊逻辑方法[D]. 绵阳: 中国空气动力研究与发展中心, 2005. KONG Y N. Fuzzy logic technique of aerodynamic modeling[D]. Mianyang: China Aerodynamics Research and Development Center, 2005 (in Chinese). [90]VAPNIK V. The nature of statistical learning theory[M]. New York: Springer-Verlag, 1995: 161-206. [91]SUYKENS J A K, VANDEWALLE J. Least squares support vector machine classifiers[J]. Neural Processing Letters, 1999, 9(3): 293-300. [92]CHEN Y L. Modeling of longitudinal unsteady aerodynamics at high angle-of-attack based on support vector machines[C]//Proceedings of the 8th International Conference on Natural Computation. New York: IEEE, 2012: 431-435. [93]WANG Q, QIAN W Q, HE K F. Unsteady aerodynamic modeling at high angles of attack using support vector machines[J]. Chinese Journal of Aeronautics, 2015, 28(3): 659-668. 汪清男, 博士, 研究员。主要研究方向: 飞行力学、 飞行器系统辨识。 Tel: 0816-2463149 E-mail: wangqing_mail@163.com 钱炜祺男, 博士, 研究员, 博士生导师。主要研究方向: 飞行器气动/飞行性能评估、 气动力/热参数辨识。 Tel: 0816-2463140 E-mail: qwqhyy@sina.com 丁娣女, 博士, 助理研究员。主要研究方向: 飞行力学、 飞行器系统辨识。 Tel: 0816-2463148 E-mail: dingdi1981@hotmail.com A review of unsteady aerodynamic modeling of aircrafts athigh angles of attack WANG Qing1,2,*, QIAN Weiqi1,2, DING Di1,2 1. State Key Laboratory of Aerodynamics of China Aerodynamics Research and Development Center,Mianyang621000, China 2. Computational Aerodynamics Institute of China Aerodynamics Research and Development Center,Mianyang621000, China Accurate unsteady aerodynamic models are the basis of control law design, flight dynamics analysis, and flight simulation of aircraft at high angles of attack. The advances in high angle-of-attack unsteady aerodynamic modeling are reviewed systematically. The developed modeling methods can be classed into two categories: mathematic methods and artificial intelligent methods. The mathematic models include those in the form of aerodynamic derivatives, nonlinear indicial response, internal state-space, differential equations, hybrid representation of nonlinear indicial response and internal state-space, flow incidence rate, etc. They are based on the understanding of unsteady flow phenomenon and mechanism. The intelligent methods, including fuzzy logic, neural networks, and support vector machines, avoid the complicated flow mechanism and are suitable to black-box system modeling especially. For individual aerodynamic models, their modeling ideas and methods and typical applications are described, and brief comments on their distinguishing features and limitations are put forward as well. Finally, the problems in current unsteady aerodynamic modeling researches and the future development directions are indicated. high angles of attack; stall/post-stall; unsteady aerodynamics; aerodynamic model; wind tunnel test; flight test 2016-01-11; Revised: 2016-02-15; Accepted: 2016-03-07; Published online: 2016-04-0517:04 . Tel.: 0816-2463149E-mail: wangqing_mail@163.com 2016-01-11; 退修日期: 2016-02-15; 录用日期: 2016-03-07; 时间: 2016-04-0517:04 www.cnki.net/kcms/detail/11.1929.V.20160405.1704.010.html .Tel.: 0816-2463149E-mail: wangqing_mail@163.com 10.7527/S1000-6893.2016.0072 V211.4 A 1000-6893(2016)08-2331-17 引用格式: 汪清, 钱炜祺, 丁娣. 飞机大迎角非定常气动力建模研究进展[J]. 航空学报, 2016, 37(8): 2331-2347. WANG Q, QIAN W Q, DING D. A review of unsteady aerodynamic modeling of aircrafts at high angles of attack[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2331-2347. http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn URL: www.cnki.net/kcms/detail/11.1929.V.20160405.1704.010.html7 迎角速率模型
8 神经网络模型

9 模糊逻辑模型
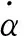

10 支持向量机模型
11 结 论
