多体动力学仿真分析在消防车变幅机构计算中应用

2016-11-14张军高志刚白冰

专用车与零部件 2016年3期

关键词：变幅油缸消防车

张军　高志刚　白冰

（徐工消防安全装备有限公司，徐州 221004）

多体动力学仿真分析在消防车变幅机构计算中应用

张军高志刚白冰

（徐工消防安全装备有限公司，徐州 221004）

消防车臂架变幅机构计算主要是铰点力求解及变幅缸行程的确定，若采用经典理论计算，是一个比较繁琐的过程，需要建立复杂的数学模型，而且机构在运动过程中，力臂也在不断变化，需要选取多个典型工况进行计算对比分析，寻求最大解，费时费力。而应用ADAMS多体动力学仿真软件很容易就解决了这些问题，只要把模型建立好，定义模型质量，添加约束和载荷，通过仿真分析，就能提取想要的力、位移、角度、速度、加速度曲线。

机构计算；数学模型；力臂；ADAMS；多体动力学；仿真

引言

消防车臂架变幅机构是单自由度平面六连杆运动机构，如图1所示：其工作原理是通过变幅缸1的伸缩带动连杆机构运动，从而实现驱动折叠臂2相对于伸缩臂5展收作业的。

图1　臂架变幅机构示意图

1　模型建立

将PRO-E变幅机构模型导入到ADAMS平台中，如上图所示，根据模型的运动关系定义约束和驱动。

图2　臂架变幅机构分析模型图

2　定义质量和载荷

将各部件的质量定义到机构各杆件中，折叠臂600 kg，变幅缸180 kg水炮喷射反力2 000 N，喷射角度斜向上与水平成30°。

图3　油缸长度随时间变化曲线

3　分析过程

（1）根据设定的变幅角度来求解油缸的全伸长度。假设臂架等角速度变幅20 s实现折叠臂相对伸缩臂0～175°变幅来进行仿真分析，可求解变幅缸的长度随时间变化曲线，如图3所示，软件同时提供图表数据转化功能，从而得到油缸的行程为1 615 mm～2 732 mm。

图4　臂架变幅角度、角速度、角加速度随时间变化曲线

图5　伸缩臂0°时油缸受力随时间变化曲线

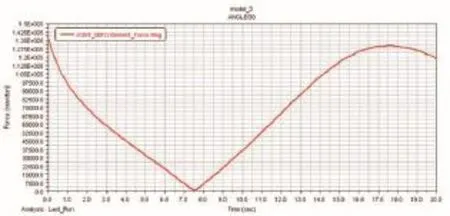
图6　伸缩臂30°时油缸受力随时间变化曲线

图7　伸缩臂60°时油缸受力随时间变化曲线

图8　伸缩臂83°时油缸受力随时间变化曲线

图9　非喷水工况伸缩臂0°时油缸受力随时间变化曲线

（2）因变幅机构是通过油缸伸缩来驱动的，油缸运动近似匀速直线运动。因此，仿真分析油缸受力则需通过给定油缸速度，从而求解臂架变幅角速度、角加速度以及各铰点的受力，根据油缸行程求解出20 s折叠臂变幅油缸伸缩速度：（2 732-1 615）/20=55.85 mm/s，绘制臂架变幅角度、角速度及角加速度如下图所示：其中红线为角度曲线，蓝色虚线为角速度曲线，粉色虚线为角加速度曲线，从图中可看出初始加速度较大，5 s后趋平缓，而臂架消防作业伸缩臂和折叠臂夹角通常大于90°，此时臂架变幅加速度小，臂架微动性、稳定性好。

（3）连杆机构确定后，给定油缸初始速度，那么臂架变幅的角速度和角加速度就定了，跟伸缩臂变幅角度无关。但油缸力的大小与伸缩臂与水平面的角度有很大关系，通过旋转重力坐标来模拟伸缩臂不同角度下的折叠臂变幅工况。得到0°、30°、45°、60°、83°的变幅缸受力曲线分别为：

从图5～图8中可看出，当伸缩臂初始角度为0°时，油缸受力较大，此时为拉力，大概15.5 t，随着伸缩臂角度的增加，油缸初始力越来越小，因为折叠臂重力的力臂在不断变小。第一个拐点出现是在折叠臂与水平面垂直的情况，此时油缸力接近为0，随着折叠臂的举升，油缸力逐渐变大，此时油缸为推力，得出最大推力为13 t，其他几个角度下最大推力和拉力都小于0°工况。因此得出油缸的最大推力为13 t。

因伸缩臂0°且伸缩臂与折叠臂夹角也为0°的工况是收臂工况，此时不喷水作业，因此计算油缸最大拉力时，仿真分析需去掉水炮喷水载荷，得到的油缸力曲线如图9所示：此时油缸最大拉力为12 t。