基于区间数排序的住房选择方案评价研究

陈　政，武永祥，王丹爽

（哈尔滨工业大学 管理学院，黑龙江 哈尔滨 150001，E-mail：cz18196373@163.com）

基于区间数排序的住房选择方案评价研究

陈政，武永祥，王丹爽

（哈尔滨工业大学 管理学院，黑龙江 哈尔滨 150001，E-mail：cz18196373@163.com）

随着我国房地产市场化的深入发展，消费者可根据自身需求自由选择住房。然而住房选择的影响因素是多维度的，且许多指标具有较强主观性，对消费者而言，很难对不同住房方案进行量化分析和综合评价。针对这一问题，从消费者角度出发，基于优序数原理和区间数排序方法，提出一种非确定条件下的住房选择方案评价方法，并结合哈尔滨市4处新开发楼盘进行实例分析，来证明该方法的有效性。此外，也可作为开发企业和第三方资讯机构进行住房市场调研分析的一种重要方式和参考依据。

住房选择；区间数排序；优序数原理；方案评价

住房选择问题的本质是消费者居住需求和住房商品的匹配问题，但由于大多住房评价指标具有较强主观性，加上消费者自身思维的模糊性，使得住房选择方案评价要在一定非确定条件下完成。在消费者住房选择的研究中，大量学者从单一因素进行研究，如郑思齐等［1］研究了通勤成本与住房成本之间的均衡关系；郝前进等［2］探求了住房与CBD（Central Business District）距离和可达性对住房价格和住房选择的关系。也有学者着眼于某一维度因素；如周京奎［3］从经济性维度着手，探究购房者收入情况、家庭结构对其住房选择的影响；胡卓玮等［4］从区位性维度着手，利用次序加权平均算法对消费者住房区位选择进行分析。通过文献梳理不难发现，学者大多着眼于住房选择各因素之间的作用机理，却鲜有从消费者角度出发，研究消费者如何就多个影响因素进行住房方案的综合评价。

由于消费者对住房选择方案评价的主观性和不确定性，本文借鉴模糊数学的不确定性指标评价模型，提出一种基于区间数排序的住房选择方案评价方法。该方法不仅是消费者住房选择方案评价方法研究的有效补充，也是优序数原理和区间数排序方法解决现实问题的一种实例论证。

1　区间数排序方法基本原理

1.1模糊评价方法基本概述

模糊评价是基于模糊数学原理，解决不确定性多属性决策问题的一种综合评价方法，它主要针对于评价指标值为不确定数的一种方案综合评价方法，常用的模糊评价方法包括模糊层次分析法和区间数排序方法等。模糊层次分析法是运用层次分析法解决指标值为不确定数的一种综合评价方法，该评价方法需要给评价指标划分层次，定性程度较大，操作过程繁琐。区间数评价方法是利用概率论原理，通过构建区间数比较的可能度矩阵，从而得出方案综合评价的结果［5］。运用区间数排序方法进行综合评价，无需给指标划分多个层次，也减去了分层估计权重值的步骤，因此区间数排序方法大大降低了评价结果的主观性和繁琐性。在区间数排序方法提出的短短十多年里，各界学者不断就区间数排序方法进行完善和优化，使得区间数排序方法原理更为成熟，如吴冲等［6］提出一种综合考虑隶属度，基于改进得分函数的直觉模糊多属性决策方法针对属性权重信息未知的决策问题进行研究，陈春芳等［7］提出等级偏好优序法，并将其运用到区间数排序方法之中，大大简化了区间数排序方法的计算流程。谭吉玉等［8］将传统TOPSIS方法与区间数排序结合，利用相对贴近度原理对区间数进行排序，使区间数排序结果更为准确。

然而在文献资料的梳理中可以发现，大量学者着眼于区间数排序方法的优化改进，在实例分析部分多是采用简单的算例，鲜有学者利用区间数排序方法解决实际问题。本文提出基于区间数排序的住房选择方案研究方法，结合了优序数原理和区间数排序方法，基于购房者视角，对4个住房选择方案进行综合评价，填补了区间数排序方法在现实应用中的空白。

1.2可能度矩阵与优序数法原理

可能度矩阵（Possibility Degree Matrix）是区间数排序常用的方法之一，它表示的是区间数之间比较大小的可能性程度，其构建方法是根据特定区间数可能度公式，算出两区间数间A大于等于B的概率［9］，并依此构建区间数之间的相互比较矩阵，由于可能度计算方法是基于概率论原理，使得区间数排序方法的计算结果更为客观，准确。

优序数法是指综合诸多评价指标，将待评价方案进行两两比较，分别计算出各方案在比较中的占优次数，将其称为方案优序数。最后，将方案优序数进行比较，排出方案的优劣次序的方法，即成为优序数法。优序数方法最初用于系统工程的研究中，是系统评价的一种有效方法。由于此方法应用简单，且在实际运用中具有保序性（即不管指标值扩大缩小一定倍数，也不会改变方案排序），优序数法被广泛运用于其他指标综合评价方法之中。如高峰记［10］将优序数法与可能度矩阵法结合，极大改进了区间数排序综合评价方法的计算效率。

1.3模糊区间数基本定义

定义1：A=［aL，aU］=｛X| aL≤X≤aU｝，称A为一个区间数，如果aL=aU，则A为一个实数。

定义2：A=［aL，aU］，B=［bL，bU］为两个区间数，其四则运算法则如下［11］：

定义3：设A=［aL，aU］，B=［bL，bU］，P（A≥B）表示A大于等于B的可能度。根据区间数可能度公式可求出［12］：

当aL＞bU时，P（A≥B）=1

当bU＞aU≥bL＞aL时，

当bL＞aU时，P（A≥B）=0

定义4：在区间数组Ai（i=1，2，…n）中，设其相互比较的可能度矩阵为P=（Pij）n×n，称矩阵P第i行元素Pij（i=1，2，…，n）中大于0.5的个数表示区间数ai的优序数，记为Ʈ（ai）。

1.4区间数排序方法通用步骤

（1）计算指标值初始决策矩阵。收集整理数据，根据评价方案的指标值，建立指标值的初始决策矩阵。

（2）初始决策矩阵规范化。设S=｛S1，S2，…，Sm｝表示备选方案集合，Q=｛Q1，Q2，…，Qn｝表示评价指标集合，C=［Cij］m×n表示指标数值初始决策矩阵。其中，表示方案集合中Si对应评价指标集合中Qj的指标值。在评价指标集合中，根据评价指标的性质，常分为“效益型指标”和“成本型指标”两种，即指标数值越大越好的表示为“效益型”指标，如小区绿化率，小区交通便利度等，指标数值越小越好的指标为“成本型”指标，如房屋总价，公摊面积等。为了便于计算和消除指标值之间的量纲，需要对初始决策矩阵中的指标值进行预处理，将所有指标值标准化：

Qj为成本型指标：

Qj为效益型指标：

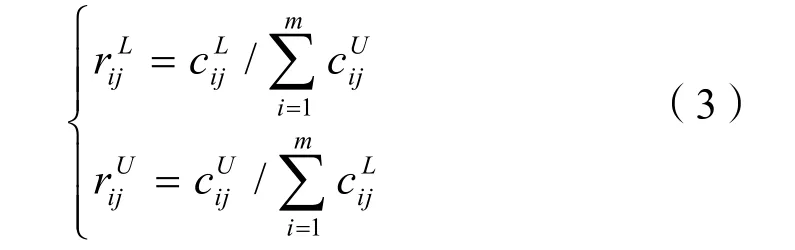
同理，指标权重值Wj也将依照上述方法进行标准化。经过一系列标准化处理，得到标准化决策矩阵R=［rij］m×n。

（3）计算各方案综合评价值。得到标准化决策矩阵，利用下式计算，可以得到方案集合中各个元素的综合评价值。

式中，rij表示第i个方案在第j个指标下的标准化指标值；Wj是第j个方案的评价指标标准化权重区间数。利用式（1）中的区间数乘法法则和加法法则，可以计算出方案综合评价值Zi。

（4）建立方案评价值可能度矩阵。根据定义3的区间数可能度计算公式，可以计算出方案集合的区间数可能度，从而建立方案集合的可能度排序矩阵，记为P=（Pij）n×n。

（5）找出各指标值优序数，并排序。根据定义4，算出各方案集合优序数，可以证明，两个区间数组Zi，Zj（i，j=1，2，…n），若Ʈ（Zi）＞Ʈ（Zj），则区间数Zi拟大于Zj，记为Zi≻Zj，且具有保序性。因此，可以根据优序数大小，对各方案集合进行比选排序。

2　评价指标体系的建立

住房选择评价指标多种多样，从不同角度建立的评价指标体系也不尽相同，在现有研究中，国外学者主要从消费者居住体验角度出发，着眼于安全性、健康性、便利性和舒适性等几个维度［13］，以居住环境为出发点，选取住房选择评价指标。但由于中国国情的特殊性，在置业购房时，消费者除了考虑自身居住体验外，还将许多现实和社会因素指标纳入住房选择评价指标体系之中，如小区居住人群、义务教育资源、上下班交通距离及拥堵情况等。在中国住房选择评价体系的研究中，Di Wu等［14］住房选择指标体系分为经济需求、住所需求和文化需求3个维度，利用因子分析法对中国一线城市数据进行分析，筛选出住房价格在内的10个评价指标。陈文君等［15］基于“宜居城市”理论，对生活、安全、出行等6个维度32个指标进行调查分析，得出影响消费者住房选择的最重要的8个指标。

本文通过对已有评价指标体系文献进行梳理，结合住房选择作用原理，“宜居城市”分类方法，从房屋属性、区位属性和服务属性3个维度出发，初步选取出18个住房选择评价指标，为更有效地对住房选择方案进行评价，排出相同类型指标的协同性影响和叠加性误差，并利用问卷调查和专家打分法对评价指标体系进行进一步筛选。

本文问卷调查专家是来自房地产开发企业、科研院所、房地产营销策划公司和房地产咨询评估机构等诸多房地产行业资深工作者，同时，为保证调查结果的有效性，也从部分有购房意向的消费者中选取代表纳入专家集合。本次专家打分问卷采取定向发放方式，总计发放37份调查问卷，回收37份，问卷回收率和有效率皆为100%。

问卷内容是对18个评价指标的重要程度打分，打分区间为0～10分，打分方式为区间数，即每个专家对评价属性重要程度打两个分值，分别代表被调查者心理最低预期和最高预期，二者构成分值区间数。具体方式如图1所示，例如某专家对一项指标最低预期为6分，最高预期为8分，则其打分区间数为［6，8］。

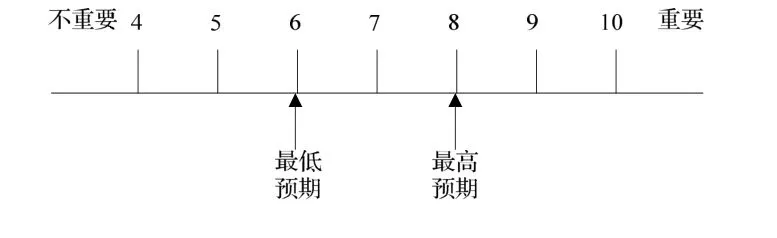
图1　问卷打分实例图

通过对专家指标打分结果的最低预期和最高预期分别求均值，归类整理，得到初始统计表，如表1所示。

根据问卷统计结果，按照重要程度打分，筛选出3个维度8个最重要影响因素，建立评价指标体系。计入指标集合Q内，分别用｛Q1，Q2，…Q8｝表示。

表1　消费者住宅选择问卷调查结果统计表

3　实例分析

3.1数据收集

以哈尔滨市为例，调查样本选取150名有购房意愿的消费者。样本数据收集方式为问卷调查。为使调查结果更为客观，选取不同年龄、身份的欲购房者为被调查对象。当被调查对象参观4个哈尔滨新开发楼盘后进行调查，为使调查结果简便，调查内容定为4个住房方案就8个指标的满意度评分，通过此项设置，所有评价指标值均为“效益型指标”，评分方式为区间数，规则和专家打分法一致。

问卷涉及的4个住房方案分别来自哈尔滨市4个不同区域（南岗区、香坊区、松北区和道里区），楼盘具体情况如表2所示。

表2　住房方案详情表

本次调查发放问卷150份，回收150份，其中有效问卷145份，问卷有效率为96.67%。调查对象主要为20～40岁这个年龄段区间，大部分被调查者在半年内有购房打算，其个人情况分布如表3所示。

表3　被调查对象年龄及欲购房时间分布

3.2住房选择方案综合评价

（1）初始决策矩阵。根据问卷调查统计结果，求出4个住房方案指标评分均值，得到指标值区间数，权重区间由指标重要程度打分表确定，依据上述信息构造指标评价初始决策矩阵，如表4所示。

表4　初始评价模糊矩阵

（2）初始决策矩阵规范化。由于指标集合各元素为满意度分值，所以指标均为效益型，即指标值越大越好。根据式（3），对初始决策矩阵进行处理，得到规范化决策矩阵R=［rij］4×8，如表5所示。

表5　规范化决策矩阵

（3）计算各方案综合评价值。根据式（4），计算出4个住房方案的综合评价值。分别为：

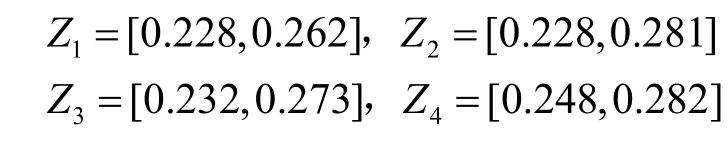
可以发现，4个住房方案区间数评价综合值都较为接近，不便于对方案优劣进行评价，所以，需利用可能度矩阵和优序数原理对其进行分析。

（4）建立方案可能度矩阵。根据定义3建立方案综合评价集合Zj=（1，2，3，4）的可能度比较矩阵P，如下所示：

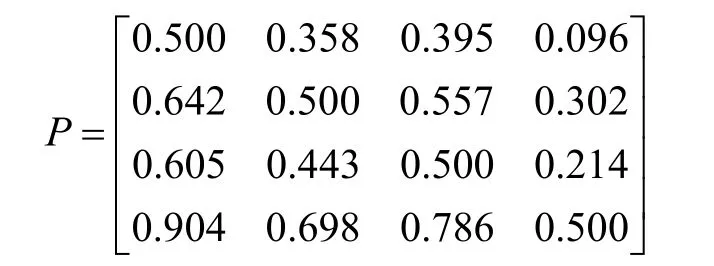
矩阵中各数值表示方案间优劣可能性程度，例如：0.358表示Z1优于Z2的可能性为0.358，0.358＜0.5，可判断Z2≻Z1，其余方案比较结果同理。

（5）计算优序数，并排序。根据可能度矩阵计算结果，结合优序数定义，计算出4个住房选择方案优序数，分别为Ʈ（Z1）=0，Ʈ（Z2）=2，Ʈ（Z3）=1，Ʈ（Z4）=3。通过优序数比较，得到4个住房选择方案的综合排序：

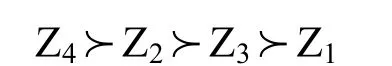
从多属性综合评价来看，4号方案优于1号方案的可能性为0.904，优于2号方案的可能性为0.698，优于三号方案的可能性为0.786，均大于0.5，其余方案依次类推。通过可能度矩阵和优序数排序可以明显看出，在房屋属性，区位属性和服务属性3个维度层8个评价指标的综合分析下，4号住房方案为最优决策方案，即在排出其他特殊原因的前提下，“保利上城”的住房选择方案为消费者的最优选择，其在房屋本身、区域地位和小区服务上至少有69.8%的可能性优于其他3个住房选择方案，消费者在这4个住房选择方案的比选中，应优先考虑4号“保利上城”的楼盘。

4　结语

住房方案选择实质上是消费者需求和住房商品的匹配过程，由于住房选择影响因素的主观性和消费者评价中不确定性的特点，本文提出一种基于区间数排序的住房选择方案评价方法，解决了不确定性条件下，消费者对不同住房选择方案的比选和决策问题。同时，本文研究也是对区间数排序方法在现实应用中的一个实证分析，论证了该方法在实际应用中的可行性。除了解决消费者住房选择问题之外，本文提出的基于区间数排序的住房选择方案评价方法，也供开发企业、房地产咨询机构和房地产研究部门对住房市场的评价和住房项目的可行性研究中，对房地产项目的开发和评价也有一定的指导性意义。

［1］郑思齐，张文忠.住房成本与通勤成本的空间互动关系——来自北京市场的微观证据及其宏观含义［J］.地理科学进展，2007（2）：35-42.

［2］郝前进，陈杰.到CBD距离、交通可达性与上海住宅价格的地理空间差异［J］.世界经济文汇，2007（1）：22-35.

［3］周京奎，收入不确定性，住宅权属选择与住宅特征需求——以家庭类型差异为视角的理论与实证分析［J］.经济学，2011，10（3）：1459-1498.

［4］胡卓玮，刘晓旭，彭程，等.基于次序权重平均法的购房选择地理空间多准则决策［J］.地理研究，2013，32（3）：476-486.

［5］李德清，韩国柱，曾文艺，等.基于布尔矩阵的区间数排序方法［J］.控制与决策，2016（4）：629-634.

［6］吴冲，刘千，万翔宇.基于改进得分函数的直觉模糊多属性决策方法［J］.统计与信息论坛，2014，29（1）：3-8.

［7］陈春芳，朱传喜，黄先玖.多属性决策的等级偏好优序法［J］.系统工程理论与实践，2012，32（7）：1506-1516.

［8］谭吉玉，朱传喜，张小芝，等.一种新的基于TOPSIS的区间数排序法［J］.统计与决策，2015（1）：94-96.

［9］肖峻，张跃，付川.基于可能度的区间数排序方法比较［J］.天津大学学报：自然科学与工程技术版，2011（8）：705-711.

［10］高峰记.可能度及区间数综合排序［J］.系统工程理论与实践，2013，3（8）：2033-2040.

［11］孙海龙，姚卫星.区间数排序方法评述［J］.系统工程学报，2010（3）：304-312.

［12］高峰记，张铁军，张海滨.基于可能度的多指标排序决策［J］.统计与决策，2012（8）：58-60.

［13］EIA W J.Decision-making theory and screening and scoping in UK practice.Journal of Environmental Planning and Management，2000，43（2）：185-203.

［14］Wu D，Mao J，Clark T N.The Influence Of Regional Culture And Value In Sustainable Development Of Chinese Urban Residential Choice［C］.Power and Energy Engineering Conference （APPEEC），2011 Asia-Pacific，2011：1-10.

［15］陈文君，尹卫红.北京城市居住适宜性评价及建设途径探讨.中国建设动态（阳光能源），2007（2）：37-40.

A Ranking Intervals Based Residential Choice Evaluation

CHEN Zheng，WU Yong-xiang，WANG Dan-shuang
（School of Management，Harbin Institute of Technology，Harbin 150001，China，E-mail：cz18196373@163.com）

Along with the development of housing commercialization，consumers could choose freely just according to their own needs，which means a completed comparison between different housing schemes. However，most of factors of residential choice are multidimensional and subjective，consumers cannot compare the different residential Choice schemes accurately. While buying a house has a great importance to Chinese customers， the objectives of the paper is to help them find a proper way to make right choices under the non-definite condition. So a residential choice evaluation based on ranking intervals is proposed in this paper，and we combine with an example of 4 new development projects in different areas of Harbin to support the feasibility and effectiveness of the method. It focuses on setting a new road for customers to make residential decisions as well as for estate developers and research institutes to use as a reference for analysis of real estate market.

residential choice；ranking intervals；optimum sequential method；scheme evaluation

F293.3

A

1674-8859（2016）05-131-05

10.13991/j.cnki.jem.2016.05.025

2016-08-04.

国家自然科学基金项目（71473061）.

陈政（1992-），男，硕士研究生，研究方向：房地产经济与管理，城市建设经济学；

武永祥（1956-），男，教授，博士生导师，研究方向：房地产经济与管理，城市建设经济学；

王丹爽（1992-），女，硕士研究生，研究方向：智慧施工，工程管理信息系统。