悬臂拼装斜拉桥安装线形与制造线形的区别和联系

周 潇

(贵州省交通规划勘察设计研究院股份有限公司， 贵阳 550081)



悬臂拼装斜拉桥安装线形与制造线形的区别和联系

周 潇

(贵州省交通规划勘察设计研究院股份有限公司， 贵阳 550081)

斜拉桥悬臂拼装时涉及到设计线形、安装线形和制造线形的概念。阐述斜拉桥悬臂拼装时其安装线形和制造线形的区别和联系，并以一段较简单的悬臂梁为例，运用数值计算对其安装线形和制造线形的区别和联系进行验证。

斜拉桥；悬臂拼装；制造线形；安装线形

斜拉桥采用悬臂拼装方法施工时，其主梁线形常常涉及到设计线形、安装线形和制造线形等概念。设计线形主要指主梁的理论成桥线形，即理论上主梁在成桥状态时的线形；安装线形主要指斜拉桥悬臂拼装过程中新建节段自由端连接形成的线形；制造线形主要指节段在工厂制作时的线形。斜拉桥悬臂拼装施工监控的目的之一就是使主梁的实际成桥线形尽可能与设计线形相吻合，而这就必然涉及施工中如何确定斜拉桥各节段的安装位置，如何在工厂制造节段等问题，即确定斜拉桥安装线形和制造线形的标高[1-3]。

目前，斜拉桥悬臂拼装施工时，其梁段的安装方法一般为切线安装法[4]。切线安装法指悬臂拼装施工过程中斜拉桥新增节段沿前一节段自由端的切线方向安装。其原理是将所有节段均按无应力状态安装，不计节段重量，节段按刚体转动。施工中，实际梁段安装时，再加载梁段重量。

本文首先从概念上阐述斜拉桥悬臂拼装时其安装线形和制造线形的区别和联系，然后以一段较简单的悬臂梁为例，运用切线安装法计算梁段的安装线形与制造线形，并通过数值验证二者的区别和联系。

1 安装线形与制造线形的区别和联系

斜拉桥主梁节段的安装线形和制造线形是完全不同的2个概念。从二者的定义看，制造线形是主梁节段在无应力状态时的线形，计算时各主梁节段均以无应力构形为初始状态。但在实际悬臂拼装过程中，新增主梁节段的安装是在前面已安装主梁节段均参与受力，即有应力状态下完成的，故二者存在本质上的区别。

虽然斜拉桥主梁节段的安装线形和制造线形本质上不同，但二者相互又有联系，安装线形需通过制造线形来实现。主梁节段在工厂按照制造线形加工完成，在斜拉桥悬臂拼装施工时，新增梁段安装后其自由端即能达到安装线形标高。

目前实际工程中，仍有部分设计人员将二者混淆，其往往将安装线形作为制造线形，从而会导致极大的误差。斜拉桥安装线形与制造线形在数值上完全相同的情况只有采用满布支架施工时才存在，因为在支架上各梁段均处于无应力状态[6]。

2 安装线形与制造线形计算

本文以一段钢悬臂梁为例，对斜拉桥梁段制造线形与安装线形的区别和联系进行计算和验证。该段悬臂梁计算模型如图1所示。该模型共划分为2个梁段，即钢梁1和钢梁2。每个梁段长度均为L，梁段节点分别以(0)、(1)、(2)表示。梁段施工采用悬臂拼装方式，并采用吊车吊装。

为了更为直观地表述斜拉桥悬臂拼装时的安装线形与制造线形，本文作如下假定：1) 计算以线弹性理论为基础，叠加原理适用[7-8]。2) 每段钢梁长度、自重均相同。3) 各节点设计线形的标高均为0，即(0)、(1)、(2)处设计线形标高均为0。4) 吊车重量不计。

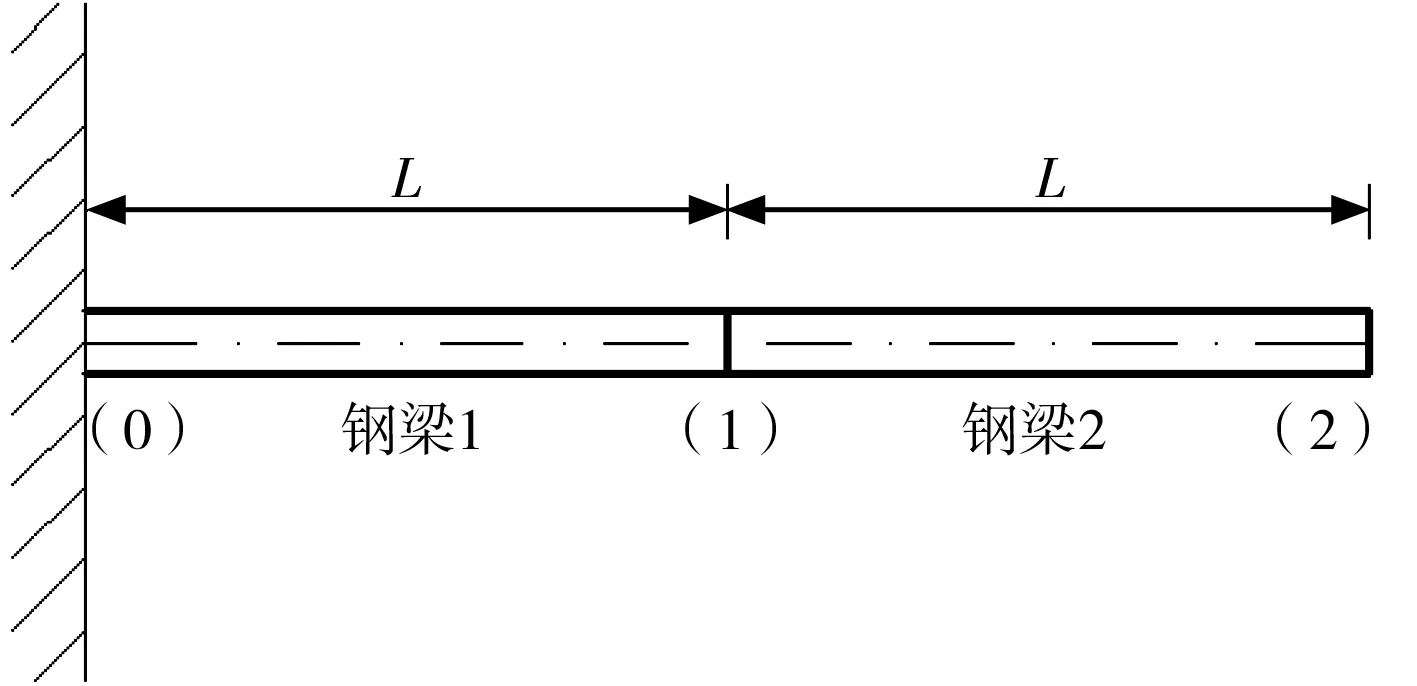
图1 悬臂梁计算模型

2.1 制造线形计算

根据切线安装法的原理，本文将斜拉桥悬臂梁计算模型分为以下5个施工阶段：1) 以无应力状态安装2段钢梁；2) 安装钢梁1；3) 吊装钢梁2；4) 安装钢梁2；5) 施加2期荷载。

斜拉桥悬臂梁制造线形计算以设计线形为初始状态时，斜拉桥悬臂梁节点在各施工阶段产生的位移如图2所示。

施工阶段1：2段钢梁均处于无应力状态，各节点均无位移发生，如图2(a)所示。

施工阶段2：安装钢梁1。钢梁1由于自重下挠，在节点1处发生位移；钢梁2未安装，仍处于无应力状态，并沿节点(1)处切线发生刚体转动，如图2(b)所示。

施工阶段3：吊车在节点(1)处吊起钢梁2。此时吊车上钢梁2的自重对钢梁1产生竖向力N和弯矩M，致使节点(1)继续下挠；钢梁2由于还未安装，仍为无应力状态，故其继续进行刚体转动，如图2(c)所示。

施工阶段4：安装钢梁2。钢梁2由于自重下挠，在节点(1)、(2)处产生位移，如图2(d)所示。

需注意的是，从施工阶段3到施工阶段4，节点(1)均存在钢梁2的自重加载，因此h13=h14。

施工阶段5：施加2期荷载。钢梁1、2继续下挠，在节点(1)、(2)处产生位移，如图2(e)所示。

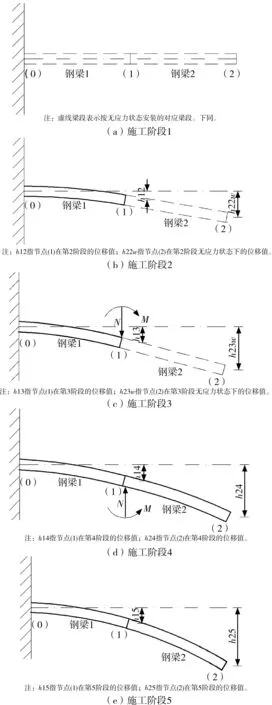
图2 斜拉桥悬臂梁节点在各施工阶段的位移

悬臂梁节点在各施工阶段产生的位移增值如公式(1)～(8)所示。

施工阶段1～2，悬臂梁模型各节点的位移增值如下：

Δh112=h12-0

(1)

Δh212=h22w-0

(2)

式中：Δh112为节点(1) 处钢梁1自重产生的下挠值；Δh212为节点(2)因节点(1)处产生下挠致使钢梁2进行刚体转动而产生的下挠值。

施工阶段2～3，悬臂梁模型各节点的位移增值如下：

Δh123=h13-h12

(3)

Δh223=h23w-h22w

(4)

式中：Δh123为吊装钢梁2时其自重致使节点(1) 处钢梁1产生的下挠值；Δh223为节点(2)因节点(1)处产生下挠致使钢梁2进行刚体转动而产生的下挠值。

施工阶段3～4，悬臂梁模型各节点的位移增值如下：

Δh134=h14-h13

(5)

Δh234=h24-h23w

根据钢材应力腐蚀开裂的机理［1］，可将其分为氢致开裂型（HE）和阳极溶解型（AD）两大类。如果阳极溶解即钢材的腐蚀对应的阴极反应是析氢过程，且释放出的氢原子分散到钢材中并对钢材裂纹的形成与扩展起决定作用，这种应力腐蚀就称为氢致开裂型应力腐蚀；如果钢材的腐蚀对应的阴极反应是析氢过程，但是释放出的的氢原子太少，不足以引起钢材的氢致开裂，钢材裂纹的形成与扩展都是由阳极溶解控制的，这种应力腐蚀就称为阳极溶解型应力腐蚀。

(6)

式中：Δh134为安装钢梁2时其自重致使节点(1) 处产生的下挠值；Δh234为节点(2)因钢梁2自重产生的下挠值。

施工阶段4～5，悬臂梁模型各节点的位移增值如下：

Δh145=h15-h14

(7)

Δh245=h25-h24

(8)

式中：Δh145为节点(1)处承受2期荷载产生的下挠值；Δh245为节点(2)处承受2期荷载产生的下挠值。

悬臂梁模型施工完毕后，节点(1)和节点(2)处产生的位移分别为h15、h25，其反向数值即为各节点的制造线形标高。

2.2 安装线形计算

采用悬臂拼装施工的斜拉桥其各梁段的制造线形可以通过以上方法计算得到。梁段按制造线形在工厂制作完成并运至施工场地后，在施工现场进行悬臂拼装施工，新建梁段自由端连接形成的线形即为安装线形。

施工阶段1：2段钢梁均处于无应力状态，各节点均无位移发生，如图3(a)所示。

施工阶段2：安装钢梁1。钢梁1由于自重下挠，在节点(1)处发生位移；钢梁2未安装，仍处于无应力状态，并沿节点(1)处切线发生刚体转动，如图3(b)所示。

施工阶段3：吊车在节点(1)处吊起钢梁2。此时吊车上钢梁2的自重对钢梁1产生竖向力N和弯矩M，致使节点(1)继续下挠；钢梁2由于还未安装，仍为无应力状态，其继续进行刚体转动，如图3(c)所示。

施工阶段4：安装钢梁2。钢梁2由于自重下挠， 节点(1)、(2)处产生位移，如图3(d)所示。

需注意的是，从施工阶段3到施工阶段4，节点(1)处均存在钢梁2的自重加载，因此h13′=h14′。

施工阶段5：施加2期荷载。钢梁1、2继续下挠，节点(1)、(2) 处产生位移，如图3(e)所示。

从施工阶段1～5的过程可以看出，钢梁1在安装前，其整个梁段均处于无应力状态，因此h15即为节点(1)处的安装线形标高；钢梁2安装时，h23w′为节点(2)处的安装线形标高。

施工阶段5完成后，钢梁1和钢梁2实际线形与设计线形的关系也可以按下式计算。

施工阶段1～2，节点(1)和节点(2)处的下挠值分别为Δh112和Δh212，在施工阶段2时有

h15-Δh112=h12′

(9)

h25-Δh212=h22w′

(10)

施工阶段2～3，节点(1)和节点(2)处的下挠值分别为Δh123和Δh223，在施工阶段3时有

h12′-Δh123=h13′

(9)

h22w′-Δh223=h23w′

(10)

施工阶段3～4，节点(1)和节点(2) 处的下挠值分别为Δh134和Δh234，在施工阶段4时有

h23′-Δh134=h14′

(11)

h23w′-Δh234=h24′

(12)

施工阶段4～5，节点(1)和节点(2) 处的下挠值分别为Δh145和Δh245，在施工阶段5时有

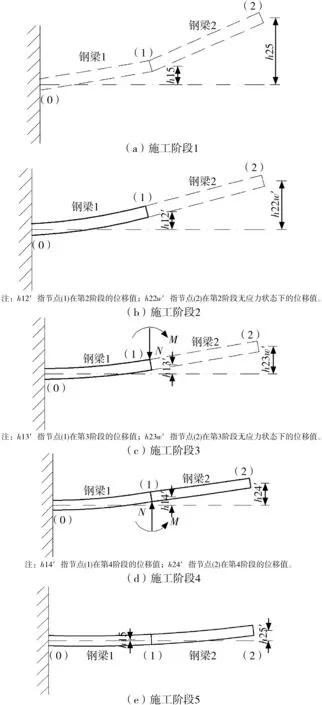
图3 斜拉桥悬臂梁节点在各施工阶段的位移

h14′-Δh145=h15′

(13)

h24′-Δh245=h25′

(14)

将公式(1)～(14)联立求解，可得到

h15′=0

h25′=0

即钢梁1和钢梁2按制造线形进行制作，在其施工完成后各节点处的实际标高与设计线形标高相吻合。

3 结论

1) 悬臂拼装斜拉桥安装线形与制造线形从概念上讲存在本质区别。制造线形计算时要求斜拉桥各梁段均为无应力状态；安装线形则是将已安装梁段的有应力状态作为计算基础。

2) 在计算梁段制造线形标高的同时也确定了安装线形标高。梁段按制造线形在工厂制作完成后，采用切线安装法进行悬臂拼装施工，新建梁段自由端连接形成的线形即为安装线形。

3) 制造线形和安装线形的标高计算主要针对钢斜拉桥。对于有混凝土参与的叠合梁斜拉桥而言，由于受混凝土收缩、徐变的影响，正向计算与反向计算无法闭合，故实际线形与设计线形不吻合。要解决此问题可以进行多次迭代计算，以使实际线形与设计线形差值在设计精度范围之内。

[1] 郝 超．大跨度钢斜拉桥的施工监控及其目标精度值[J]．中国公路学报，2003，16(1)：54-57.

[2] 狄 谨，黄 庆．无背索斜塔钢—混凝土结合梁斜拉桥施工控制仿真[J]．长安大学学报(自然科学版)，2004，24(3)：43-47.

[3] 狄 谨，武 隽．自锚式悬索桥主缆线形计算方法[J]．交通运输工程学报，2004，4(3)：38-43.

[4] 李 乔．斜拉桥悬臂施工时安装标高的计算方法[J]．西南公路，2002，1(1)：35-36.

[5] 李 乔，唐 亮．悬臂拼装桥梁制造与安装线形的确定[C]//第十六届全国桥梁学术会议论文集．北京：人民交通出版社，2004：297-302.

[6] 梁 鹏，肖汝诚，徐 岳．超大跨度斜拉桥的安装构形与预应力构形[J]．长安大学学报(自然科学版)，2006，26(4)：49-53.

[7] 何 畏，唐 亮，强士中，等．大跨度焊接钢箱梁斜拉桥施工控制技术研究及应用[J]．桥梁建设，2002(5)：17-21.

[8] 葛耀君．分段施工桥梁分析与控制[M]．北京：人民交通出版社，2003.

Difference and Similarity between Erection Alignment and Manufacturing Alignment of Cantilever Erection for Cable Stayed Bridge

ZHOU Xiao

ZHOU XiaoAbstract: The erection of cantilever on cable stayed bridge involves concepts of design alignment, erection alignment and manufacturing alignment. This paper describes differences and similarities between erection alignment and manufacturing alignment during cantilever erection. We used a simple cantilever as example to verify the differences and similarities between erection alignment and manufacturing alignment with numeric computation.

Cable stayed bridge; cantilever erection; manufacturing alignment; erection alignment

10.13607/j.cnki.gljt.2016.05.016

2016-01-18

周 潇(1982-)，男，贵州省贵阳市人，硕士，高工。

1009-6477(2016)05-0066-04

U448.27

A