流固两相流的稀疏离散相模型研究进展
2016-11-12陈彬颜欢刘阁韩超
陈彬,颜欢,刘阁,韩超
(重庆工商大学废油资源化技术与装备工程研究中心,重庆 400067)
流固两相流的稀疏离散相模型研究进展
陈彬,颜欢,刘阁,韩超
(重庆工商大学废油资源化技术与装备工程研究中心,重庆 400067)
流固两相流中稀疏离散相广泛存在于化工、储运、分离等工程实际应用中,其复杂的湍流运动规律的描述是目前两相流研究的热点和难点之一。对流固两相流中稀疏离散相模型的发展历程进行了综述和分析,从离散相轨道模型的理论依据、建模过程、数值模拟方法以及应用情况等几个方面详细地分析了离散相既定轨道模型、随机轨道模型、改进随机轨道模型等模型,并针对离散相和连续相间的相互耦合关系进行了阐述,进而对相应的模型进行了评价;并指出离散相轨道模型目前存在的问题和今后发展的方向,对连续相脉动速度进行随机处理提出基于随机Fourier级数描述离散相合力的改进随机轨道模型,从而较好地描述离散相的运动规律,同时结合考虑两相耦合的方法建立两相流的全耦合振动动力学模型,可全面、系统地描述流固两相流中稀疏离散相的运动特征,为流固两相流中稀疏离散相模型的深入发展提供前期基础。
流固两相流;离散相模型;随机轨道模型;稀疏离散相;两相耦合
化工、储运、分离领域中诸如煤粉的输送和燃烧过程、流化床/循环流化床内的气固两相流、旋风分离器中的气固分离等流固两相流一直是国内外研究的热点,流固两相流模型的建立通常根据连续相中离散相体积分数的多少分为两类:一类是当离散相体积分数大于10%~12%时,将连续相和离散相都在Euler坐标系下运用连续介质原理分别构建质量、动量和能量守恒方程,如刘大有[1]提出的连续流体模型、GIDASPOW[2]提出的双流体模型等,这类模型的离散相相间相互作用可以用固体黏度和固体压力来表示[3-4];另一类是连续相中离散相体积分数小于10%~12%时,离散相非常稀薄,不宜将其作为连续介质处理,因而离散相的运动方程采用Lagrange坐标系下牛顿第二定律建立,即离散相轨道模型[5-7],连续相的质量、动量和能量守恒方程仍采用Euler坐标系下运用连续介质原理进行建立,且这类模型的离散相相间相互作用可以用完全弹性碰撞模型或离散单元法处理。如陈彬等[8-9]建立了Lagrange坐标系下油中颗粒污染物的运方程,对连续相(油液)建立了连续介质方程,分析了油样中低含量(小于0.1%)的铜颗粒与连续流体运动黏度的内在关系。针对喷涂工艺过程离散相参数湍流特性利用离散相轨道模型对涂层力学性能影响的规律分析,获得最佳的喷涂工艺参数[10];以及利用离散相轨道模型对水击驻波场中乳化油液离散相湍流运动规律分析,为油水分离机理获得奠定了理论基础[11]。
流固两相流模型研究特别是稀疏分散相模型研究是化工、储运、分离领域的重要基础,因而近年来在工程问题的数值计算方面应用越来越广泛。在建立稀疏分散相模型时考虑到流固两相流中的连续相分为气体或液体两种类型,国内外研究中针对不同的流体可将流固两相流分为气固、液固两种类型,根据连续相(气体或液体)的不同属性,采用Euler坐标系下运用连续介质原理进行建立连续相的质量、动量和能量守恒方程考虑的影响因素不同,其中连续相为气体时要考虑相变、压缩问题,即一般要建立连续相的热力学方程,而连续相为液体时相对简单,可不考虑相变、压缩和热力学方程问题,即可略去能量方程,这对大多数的流固两相流问题是合适的[12]。由于各种两相流动过程几乎都是处于湍流流动形态,离散相轨道模型能够确切反映和模拟具有复杂物理化学反应过程的离散相的运动特征,且考虑了流体湍流脉动对离散相运动的影响因素,因而离散相轨道模型在处理离散相湍流扩散时主要有3种方法:忽略离散相湍流脉动的既定轨道模型[13]、离散相漂移速度和漂移力修正轨道模型[14]和考虑离散相湍流脉动的随机轨道模型[15-17]。因此,在实际工程应用中离散相轨道模型得到广泛的关注和发展。
为了对流固两相流中稀疏离散相的动态特征更好地分析和研究,根据稀疏离散相模型的不断发展历程,从现有离散相模型(即离散相既定轨道模型、随机轨道模型、改进随机轨道模型等)的理论依据、建模过程、数值模拟方法以及应用情况,特别对各个离散相模型研究中离散相和连续相的相互耦合关系进行了详尽的分析,指出它们的异同点,并根据离散相相应的模型应用情况进行了评价。根据离散相在Lagrange坐标系下牛顿第二定律的应用,提出一种用随机Fourier级数进行描述离散相所受合力的一种新的随机轨道模型,从而建立两相流的全耦合振动动力学模型,可全面、系统地描述流固两相流中稀疏离散相的运动特征,为实际工程应用提供理论支撑。
1 离散相既定轨道模型
根据稀疏离散相在两相流中的运动特征,既有离散相跟随连续相的运动又有两相的交叉作用提出了离散相既定轨道模型。既定轨道模型是在Euler坐标系下描述连续相运动,从连续相对离散相的湍流作用和离散相的经历效应两方面来建立Lagrange方程,且在方程中考虑了离散相的湍流扩散,使离散相的计算域扩展到整个计算流场[18-19],利用Lagrange方法建立离散相的轨迹模型,从而模拟出离散相的各种经历效应(如碰撞、聚合等)。
(1)离散相既定轨道模型
连续相的Euler模型[20]可描述为式(1)。

式中,φ为代表连续相的各个物理量,具体的数学形式如表1所示。其中,μeff= μ+ μt,i方向为轴向、径向和切向。在Lagrange坐标系中,离散相的运动方程由牛顿第二定律确定,见式(2)。

表1 连续相的各个物理量的数学形式

式中,(∑F)p为离散相所受的合力。离散相在连续相中受到的力有曳力、重力、浮力、压力梯度力、附加质量力、Magus升力、Saffman升力、Basset力等。根据不同的具体情况考虑离散相在连续相中所受的力。
(2)离散相既定轨道模型的数值方法
对于既定轨道模型的数值模拟方法主要有:单元内颗粒源(particle source in cell,PSIC)数值方法、离散相运动轨道分解法、欧拉-欧拉法和欧拉-拉格朗日法相组合的数值模拟法、基于离散单元法的颗粒群柔性轨道法、直接模拟蒙特卡罗(direct simulation monte-Carol,DSMC)法、拟谱次网格缩放模式拉格朗日法追踪法等。
采用CROWE等提出的PSIC数值方法,把离散相对连续相的作用作为连续相的质量、动量、能量、湍动能和湍流耗散率守恒方程中的附加源项,采用主动控制技术消除流体系统振动源项[21],将动量方程中作用于整体流场的总作用力分配给包含离散相的计算网格或是网格结点[22]。利用既定轨道模型和PSIC法对火药在膛内的运动速度和轨迹进行数值求解[23],两相间的相互作用反映在耦合源项中,同时考虑火药的化学反应过程,求解得到的膛压和初速度与实验值有较好的一致性。
采用离散相运动分解轨道模型,将离散相的运动过程分解为离散相相间的相互作用和连续相对离散相的作用,改进硬球模型中离散相相间相互作用的处理方法。欧阳洁等[24]采用此模型并改进了影响模拟真实性的局部空隙率,从而能有效真实地模拟鼓泡流化床的气泡形成和节涌现象。
汪靓等[25]利用Fluent计算软件模拟计算后台阶颗粒流,连续相使用雷诺应力湍流模型描述,雷诺应力湍流模型考虑了雷诺应力的各向异性,离散相使用拉格朗日方法跟踪每个离散颗粒的运动轨迹。模拟过程中考虑离散相的重力作用,忽略其他的作用力。模拟结果表明了由于连续相对离散相的影响,流场分布不均匀导致离散相分布的不均匀。
欧拉-欧拉法和欧拉-拉格朗日法相组合的新数值模型[26],即利用基于Chapman-Enskog理论[27]的微元流体动理学方法模拟计算在欧拉坐标系下稠密离散相相间的相互作用,利用离散相随机分布模型计算在拉格朗日坐标系下的离散相湍流扩散,考虑连续相与离散相相间的黏滞力,流体脉动速度用随机Fourier级数表达。利用这种新模型对循环流化床燃烧器的上升段数值模拟,结果表明数值结果与试验数据两者能够较好吻合,说明该混合模型能有效地模拟浓相气固两相流。
考虑到离散相相间的碰撞,采用基于离散单元法(discrete element method,DEM)的离散相群轨道柔性模型,连续相用两相耦合的Navier-Stokes方程表达,离散相相间的相互作用用离散单元法表达[28]。对三维管道中流固两相流进行数值模拟时,只考虑曳力和离散相与连续相的双向耦合作用,模拟了传统的不考虑离散相相互作用的两相流模型和柔性离散相群轨道模型在同一物理模型条件下前6个颗粒沿y-z平面的粒子轨迹图,如图1所示。
由图1可知离散相碰撞之前,两种模型的计算结果一致,而碰撞之后,离散相轨道发生很大的变化,不考虑离散相相间相互作用的传统两相流模型无法正确描述碰撞后离散相的运动,而有碰撞时间的柔性碰撞更能模拟碰撞的实际情况。
离散相相间的相互碰撞问题运用硬球模型描述,对突扩圆管和节流器内液固两相流进行数值模拟[30-31],可以真实地模拟突扩圆管和节流器内离散相的非均匀分布特性和运动过程,得到单个离散颗粒的速度、碰撞角度、碰撞位置等运动特性等。利用DEM还可以运用于模拟矩形流化床中的气固两相流的流动特征[32]和流化床内木材气化过程[33]。利用离散单元法和计算流体动力学(discrete element method- computational fluid dynamics,DEM-CFD)方法结合描述瞬态离散相与连续相的交互作用,如CHU等[34]利用CFD-DEM模型数值计算了重介质旋流器内煤粉的冲击磨损运动,表明磨损严重部位是插口的内墙和外墙的排气管;KRUGGEL和OSCHMANN[35]模拟了气力输送过程中水平管与垂直管相互连接的弯曲部位,结果表明离散相形状会导致压降、离散相速度分布、离散相之间、离散相与壁面之间和离散相与连续相之间的作用力的变化。

图1 沿y-z平面的颗粒轨迹对比图[29]
利用基于拉格朗日方法修正直接模拟蒙特卡罗(DSMC)法,通过概率抽样确定离散相碰撞事件,同时运用硬球模型关联离散相碰撞前后的速度、角速度。DU等[36]应用DSMC法和既定轨道模型模拟研究了气固两相流中离散相的行为,得到合理的离散相的运动行为、离散相浓度的分布和离散相碰撞位置,结果表明离散相碰撞主要分散在离散相碰撞区,离散相密度和离散相相间碰撞率在离散相碰撞区达到最大值。
此外,利用拟谱法模拟流动流体,使用拉格朗日法追踪离散相,模拟研究在三维混合层中大尺度旋涡结构和离散颗粒间的相互作用;或通过采用由Smagorinsky引入的著名次网格缩放模式模拟气体流场,使用拉格朗日法追踪颗粒理论研究气固两相平面尾流的大尺度旋涡结构;或是在只考虑Stokes曳力、Saffman力和重力的情况下,采用既定轨道模型数值模拟不同Stokes数情况下可压缩紊动射流中的离散颗粒的分布特征[37-39]。利用既定轨道模型对立管中的稠密气固上升流[40]和针配电器矩形气泡柱内气泡振动的动态特性[41]进行模拟研究,同时利用粒子图像测速技术(particle image velocimetry,PIV)捕获针配电器矩形气泡柱内气泡的图像和直径为50μm的气泡踪迹。
可见离散相既定轨道模型虽然应用比较广泛,但是它没有考虑湍流脉动对粒子运动的影响,不能准确反映离散相的复杂经历,具有一定的缺陷,在实际工程中的应用受到一定的限制。
2 离散相随机轨道模型
为了能够准确反映和模拟具有复杂经历的离散相,考虑到离散相脉动的各种物理因素和连续相湍流脉动对离散相的影响,在既定轨道模型的基础上发展提出了离散相随机轨道模型。在随机轨道模型中,考虑了连续相湍流脉动对离散相湍流弥散的影响,将离散相运动方程中的连续相瞬时速度分为时均速度和脉动速度,来实现跟踪离散相在连续相中的运动轨迹。根据对连续相脉动速度的随机处理方法的不同,随机轨道模型又分为直接随机轨道模型和间接随机轨道模型两种。
2.1直接随机轨道模型
(1)直接随机轨道模型


将随机确定的脉动速度u′、v′、w′代入离散相的动量守恒方程中进行连续积分,可得到离散相的轨道方程为式(4)。

(2)直接随机轨道模型的应用
直接随机轨道模型的模拟研究的应用范围较广,如陈曦等[42]对原煤暗道空间粉尘的运移扩散规律进行了数值模拟,得到的模拟结果与现场实际分布情况的实测数据基本一致;袁惠新等[43]对双入口形式分离旋流器壁面磨损情况的模拟可以得到双入口式旋流器的最大磨损位置,其壁面磨损呈对称分布;余徽等[44]实验研究和数值模拟了热泳作用下PM2.5离散颗粒在气液交叉流中的运动情况;唐婵等[45]利用离散相随机轨道模型和离散相沉积模型分别数值研究了气流中微小离散颗粒横掠圆管束表面时和飞灰横掠管束时的运动轨迹和沉积特性,获得了离散相直径对飞灰运动轨迹和沉积分布的影响。
通过在不考虑相间相互作用的条件下,离散相采用随机轨道模型,连续相采用二阶矩湍流模型对两组不同粒径的油滴群在两种典型液-液旋流分离管中的运动轨迹的模拟研究[46],结果表明随机轨道模型能够在定性上较好地说明油滴在旋流管中的分离过程,从而揭示不同粒径油滴在旋流管中的分离过程以及两种旋流管在分离特性方面的差别。
在考虑连续相与离散相之间的相互作用的情况下,在模拟过程中离散相采用随机轨道模型,连续相采用雷诺应力模型[47],建立相应的雷诺应力方程、湍动能和湍动能耗方程使连续相的连续性方程和动量方程封闭,将雷诺应力和平均速度联系到一起。如袁惠新等[48]模拟研究了固液分离旋流器壁面的磨损情况;王志斌等[49]模拟研究了不同进口区域、不同粒径情况下离散相进入水力旋流器的运动轨迹及分离特征,可以为全面揭示旋流器分离理论提供一些依据;周大伟等[50]分别对固液环缝内衬旋流器和普通分离旋流器的磨损情况的模拟研究可以得到旋流器磨损情况最严重的位置,当较大离散颗粒位于环缝内衬旋流器的内衬和器壁中时可降低环缝内衬的磨损。
应用基于瞬态颗粒动量方程的随机轨道模型,在连续相的雷诺平均N-S方程中加入RNG k-ε湍流模型[51]进行封闭,考虑连续相湍流脉动的效应。张志峰等[52]对不同颗粒直径分布下长尾喷管中离散颗粒的运动轨迹进行了数值模拟,结果表明:由于湍流脉动效应对离散相运动的影响,离散相在流场中的分布弥散程度增加,离散相与壁面的碰撞概率增加,随着离散相直径的增加,湍流脉动对离散相的作用减小,如图2所示。随机轨道模型相对于既定轨道模型获得的结果,流场中几乎不存在无离散相区域,同时表明了离散相和壁面碰撞的形式主要为小直径离散颗粒主要受湍流脉动的作用,大直径离散颗粒主要是由于惯性的作用。

图2 离散相运动轨迹比较[52]
基于随机轨道模型,利用PSIC方法计算流固两相耦合,刘静和徐旭[53]对喷管内气固两相流进行了模拟研究,将随机轨道模型和既定轨道模型的数值结果与实验结果进行比较,结果表明随机轨道模型对实际湍流流动现象的模拟优于既定轨道模型,且随机轨道模型对离散颗粒运动轨迹的模拟更接近实验现象,特别是对湍流度大的喷管两相流动,如图3所示。
对于随机轨道模型中离散相可以采用雷诺应力模型、雷诺时均方程与标准k-ε模型对连续相进行描述[54],采用Fluent软件中离散相模型(discrete particle model,DPM)中的随机轨道模型描述方法,通过U-beam分离器内进口处鳃片的不同角度对气固两相流进行了数值模拟,结果表明当进口处鳃片角度为35°时会导致停滞区产生并收集离散相,也会导致旋转结构的变化,还会使挡板内的湍流强度降低,促进离散相分离,提高了U-beam分离器的性能。可利用低雷诺数k-ε双方程模型和随机轨道模型研究垂直管内液固两相流流动对壁面的冲刷腐蚀过程机制[55]和低浓度离散相对单喷嘴气泡的影响过程[56]。而覃先云等[57]则采用Realizable k-ε 湍流模型模拟连续相,利用随机轨道模型模拟离散相在扫路车吸嘴内腔中的运动轨迹和湍流脉动对离散相的影响。

图3 平均直径为dav=6.2μm的粒子位置分布[53]
此外,在雷诺平均湍流模型中纳入光滑粒子流体动力学(smoothed particle hydrodynamics,SPH)方法[58]来描述湍流的影响,所得数值结果与实验观测结果吻合较好。RAMANUJACHARI等[59]使用随机轨道模型理论研究了湍流气流离散相分布,脉动速度从高斯分布随机抽样,使用随机行走模型计算可得到离散相轨迹,当连续相与离散相的时均速度相同时,通过随机轨道模型计算得到离散相的湍流扩散系数与实验数据一致。
可见直接随机轨道模型是将连续相的脉动速度根据连续相湍动能以及假设的概率密度函数用一个随机数表示。很难全面反映连续相的脉动速度的变化规律,因而在直接随机轨道模型的基础上又发展了间接随机轨道模型。
2.2间接随机轨道模型
间接随机轨道模型(脉动频谱随机轨道模型)是基于PSIC方法,更全面地研究离散相的湍流扩散的一种随机轨道模型,可以反映出连续相的湍流运动是由不同周期、不同方向和不同振幅的三维脉动随机叠加作用形成。该模型使用k-ε双方程湍流模型求解连续相湍流场,将连续相的瞬时速度ui分解为时均速度和脉动速度,根据连续相湍流脉动的频谱、能谱曲线,用随机Fourier级数来模拟连续相的脉动速度,采用拉格朗日法描述不同尺寸组的离散颗粒群的轨迹运动,同时包含流固两相流的相间耦合作用。

利用间接随机轨道模型[60]模拟计算气固多相射流和流化床中离散相的运动轨迹,通过体积统计平均法求得的离散相速度场和浓度分布能较全面地反映不同粒径的离散相湍流扩散作用和离散相平均速度滑移,数值计算结果与实验数据较为吻合。对剪切紊流中不同流体雷诺数下的流体速度、离散相的运动速度和轨迹进行模拟计算[61],对比分析间接随机轨道模型的数值计算结果和实验研究结果,表明间接随机轨道模型能够很好地描述离散相在剪切紊流中的运动。
此外,结合湍流的脉动频率-频谱与平均特性来模拟湍流流场[62],湍流脉动速度用Fourier级数表述为式(6)。

运用湍流频谱的基本特征和频谱指数的特性确定湍流频谱分布函数的表达式为式(7)。

间接随机轨道模型不论是基于PSIC方法的脉动频谱随机轨道模型还是结合湍流的脉动频率-频谱与平均特性来模拟湍流流场,都较全面地反映出连续相的湍流运动的真实性。对于模拟计算各向同性湍流和自由射流,间接随机轨道模型适用于均匀各向同性的湍流扩散和具有复杂形状的工程湍流流场,表现出了较好的模拟效果。但在随机轨道模型中离散相的运动方程虽然考虑了连续相湍流脉动对离散相湍流弥散的影响,而这种影响是间歇的。这种间歇式的作用会导致随机轨道模型所预报的离散相的湍流脉动小于真实值,因而在随机轨道模型的基础上提出了一种改进的随机轨道模型。
3 改进随机轨道模型
为了克服随机轨道模型的离散颗粒湍流脉动预报值低于真实值这一不足,把两相之间的湍流相互作用作为一个连续过程考虑,因此,张会强等[63]提出了一种改进的随机轨道模型,即把离散相看成一个个具有相同速度、大小和经历的离散颗粒群,离散相的时均量在由离散相湍流脉动所确定的随机轨道上输运,考虑到流固两相流中离散相较为稀疏,因此忽略离散相相间的相互作用、压力梯度力、虚假质量力、Basset力和Magnus力等。
离散相在i方向(轴向、径向和切向)的时均速度和湍动能的输运方程见式(8)、式(9)

离散相的随机轨道方程为式(10)。

离散相的脉动速度用随机方法处理,如式(11)。

张会强等[64]使用该模型对突扩液固两相流动进行了模拟研究,连续相的湍流运动用k-ε模型来描述,离散相用改进的随机轨道模型进行描述,连续地考虑了影响离散相湍流脉动的经历效应和离散相所在位置流场影响的当地效应,并采用Monte-Carol随机采样方法获取了离散相的脉动速度,将计算结果和实验结果进行了比较,检验了该改进模型的合理性,改进后的随机轨道模型模拟得到的两相轴向速度和湍动能与实验符合得很好。
针对改进随机轨道模型的特点,利用随机过程处理方法求解流固两相耦合脉动量与连续相Reynolds应力关系,从理论上完善改进的随机轨道模型,用离散相平均速度方程和离散相Reynolds应力轨道方程来替代原来的离散相速度方程,离散相正Reynolds应力轨道方程表达式为式(12)。

徐江荣等[65]利用这种新的处理方法与张会强提出的改进随机轨道模型分别对各向同性湍流衰减流场进行模拟,将两种处理方法的模拟结果与试验结果进行对比,得出离散颗粒的脉动均方根速度如图4所示。
图4(a)为无外力时,使用改进随机轨道模型与新处理方法模型分别模拟了直径为5μm的离散颗粒的脉动均方根速度,两种模型的模拟结果几乎没有差别,与实验结果也十分吻合,说明小的离散相几乎与气体具有相同的湍流强度,且在瞬间被气流脉动同化。图4(b)为无外力时,使用改进随机轨道模型与新处理方法模型分别模拟了直径为57μm的离散颗粒的脉动均方根速度,改进随机轨道模型模拟结果显示,离散相脉动被气流同化的时间短,之后脉动均方根速度又低于实验值,最后又略高于实验值;而新处理方法模型的模拟结果显示,离散相脉动被气流同化的时间长,与实验结果非常吻合。结果表明新处理方法模型比改进随机轨道模型模拟计算更为准确,且计算量小、统计更加方便。

图4 无外力时离散颗粒的脉动均方根速度[65]
还可以通过建立离散相的雷诺应力拉格朗日方程,推导得到两相耦合脉动量拉格朗日方程,使用经验公式计算两相耦合脉动量。将离散相雷诺应力的拉格朗日方程平均化可得到式(13)。



连续相脉动关联Rff(t1,t2)可由连续相雷诺应力获得,这样就可以通过式(14)解得Rfpi(t1,t2),当t1=t2=t时,可进一步求得两相耦合脉动量。
利用以上方程组,李昭祥和徐江荣[66]模拟研究了Wells和Stock的风洞实验的离散相运动特性,特别是离散相的湍流扩散特性,将模拟结果和实验结果进行比较,结果表明,新模型离散相的湍流强度与实验值更为相符,但需进一步探讨该模型中离散相雷诺应力随外力的变化情况。
在仅考虑作用在离散相上的气体阻力而忽略其他各种力的情况下,可以通过不同Reynolds数范围内的气体-颗粒阻力系数表达式推导出离散相运动方程的一组分析解[67],对分析解进行比较分析,表明由各种阻力系数公式得出的离散相速度和轨迹的表达式均与离散相松弛时间τrp有关。可以利用得到的离散相运动速度与轨迹的解析表达式,在离散相轨道和随机轨道模型的计算中,在已知离散相运动的时间间隔取为湍流随机涡团的生存周期时,直接求出离散相运动的终端位置与速度。
4 离散相的其他模型
在流固两相流研究中,求解离散相在连续相中的运动特性和轨迹,除了既定轨道模型、随机轨道模型和改进随机轨道模型以外,还有一些求解离散相运动特征的其他模型,如离散相的PDF方程[68-70]、湍流颗粒浓度模型等。
4.1离散相的PDF方程
利用离散相随机轨道方程推导得到离散相速度的概率分布函数(probability density function,PDF)方程,以降低两相流离散相PDF模型在位置-速度相空间上的高维方程维数,概率分布函数PDF方程的表达式为式(15)。

从而推导出离散相的平均速度,见式(16)。

概率分布函数PDF方程的定态解的高斯分布形式为式(17)。

由于随机轨道中的连续相速度脉动量由连续相湍流应力和随机数共同确定,因此,在新的求解方法中,离散相位置仍然由常用的随机轨道模型中了离散相位置方程计算确定,离散相的速度和脉动速度由式(16)和式(17)确定。
郭国庆和徐江荣[71]利用常用随机轨道模型与离散相速度PDF轨道方法分别对Wells和Stock的风洞实验进行模拟,对两种模型的模拟结果进行比较分析,结果表明离散相速度PDF轨道方法在模拟离散相湍流扩散时比常用的随机轨道方法计算量小,统计结果的光滑性和精度更优,新位置的离散相速度计算更方便、精确。
XU等[72]基于离散相的PDF输运方程,利用离散相的二阶矩轨迹模型对气固两相流进行模拟,得到了离散相合理的统计特征。
离散相PDF模型引入湍流中颗粒运动的概率密度分布函数(PDF),建立和求解封闭形式的PDF输运方程,获得颗粒相的各守恒方程和本构关系,具有信息丰富、守恒方程封闭简单等优点,但由于PDF方程闭合和求解的困难,离散相PDF模型常用于简单流动场合。
4.2离散相湍流浓度模型
离散相湍流浓度模型是根据Prandtl湍流混合长理论,将离散相的湍流扩散分为两部分:连续相湍流运动对离散相扩散的影响和离散自身的湍动对离散相扩散的影响,即离散相输送是连续相湍流卷吸效应和离散相自身湍动的相互作用的结果。
离散相湍流浓度方程具有对流-扩散方程的形式,其标准输运方程形式[69]为式(18)。

数值求解对流-扩散方程是否收敛的关键在于源项是否线性,离散相湍流浓度模型的源项线性较好,方程的收敛性好,易于求解。
顾璠等[73]对气固两相流动离散相湍流扩散现象进行了理论分析,推导出离散相湍流扩散系数来表征离散相的湍流扩散特性,离散相湍流扩散系数Dt的表达式为式(19)。
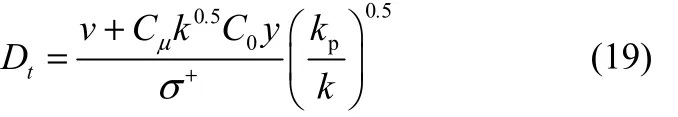
运用离散相湍流浓度模型对直管气固两相流动和受限射流气固两相流动分别进行了数值模拟,直管内离散相的输送主要取决于连续相湍流涡的卷吸效应,模型对于湍流边界层内的流动是成功的。
离散相湍流浓度模型由于湍流模化理论的限制,未能很好地模拟离散相的弥散特征,说明该模型存在一定范围的适用性和局限性,在复杂气固两相流场的模拟还需进一步研究改善。
5 离散相模型中两相的耦合关系
从以上稀疏离散相模型的发展历程上看,除了离散相既定轨道模型外,其他模型都考虑了连续相和离散相二者的相互影响关系,其中当离散相浓度小于6.5%时,可忽略离散相对连续相的作用使用单向耦合;当离散相浓度大于6.5%时,离散相对连续相的作用强烈,不能忽略两相间的相互作用,须使用双向耦合[74]。早期的研究者一般假设流体湍动能和湍流耗散率的附加源项为零,实际上离散相的存在必然会对连续相的流动产生影响。大多数研究者均采用了PSIC方法来实现流固相间双向耦合。PSIC方法是把离散相对连续相的作用作为连续相的质量、动量、能量、湍动能和湍流耗散率守恒方程中的附加源项,将动量方程中作用于整体流场的总作用力分配给包含离散相的计算网格或是网格结点。此外,连续相模型中必须加入连续相与离散相相互作用而产生的附加源项[75]。
采用PSIC方法计算喷管内两相流和火药在膛内的气固两相流中的两相耦合,连续相和离散相的相互作用会导致两相流中的连续相流场速度下降。对三维管道中流固两相流进行数值模拟时,采用PSIC方法在连续相模型中加入连续相-离散相两相相互作用而产生的附加源项来描述离散相对连续相的反作用耦合现象,模拟结果表明考虑了离散相与连续相的双向耦合作用后,有碰撞时间的柔性碰撞比不考虑离散相相间相互作用的传统两相流模型更能模拟碰撞的实际情况。
王志斌等[49]考虑了两相耦合作用,对旋流分离器的模拟形象地反映出离散相在旋流器中的分离过程,由内旋流、短路流和循环流带出后从溢流口逃逸的大直径离散相是影响旋流器分离效率的关键,为全面揭示旋流器分离理论提供了一些依据。CHEN等[76]在考虑了连续相与离散相之间的相互作用、离散相与离散相之间和离散相与壁面之间的碰撞下,连续相采用标准模型,结合CFD-DEM数值模拟了弯曲角对弯管侵蚀、离散相运动和流场变化的影响。
基于牛顿第三定律建立离散相与连续相的相间耦合关系:一类是将双流体模型中连续相方程的耦合项推广到离散相轨道模型,再反作用于离散相;一类是将控制微元体内所有单个离散颗粒的曳力进行叠加,再利用反作用原理推导出连续相控制方程的耦合项。欧阳洁等[77]利用确定性颗粒轨道模型研究了不同的相间耦合关系和曳力公式模拟气固循环流化床的影响,其瞬态图像如图5所示,研究结果表明在确定性颗粒轨道模型中基于离散相曳力模型进行相间耦合时,WEN和YU[78]的曳力公式以及DI FELICE曳力公式能较好地模拟鼓泡流化床与循环流化床的基本流动特征,而基于双流体模型的相间耦合关系对气固流化床模拟的合理性尚需进一步研究。

图5 循环流化床的离散相分布[77]
6 模型的评价与展望
离散相的既定轨道模型能够有效地模拟流固两相流中离散相的运动轨迹,在流固两相流实际应用工程方面具有一定的指导意义。但是它没有考虑湍流脉动对粒子运动的影响,不能准确反映的离散相的复杂经历,具有一定的缺陷,在实际工程中的应用具有一定的限制。
随机轨道模型充分考虑了影响离散相脉动的各种物理因素和离散相湍流脉动对离散相的影响,比既定轨道模型更能准确模拟连续相对离散相的弥散影响。但在随机轨道模型中离散相的运动方程虽然考虑了连续相湍流脉动对离散相湍流弥散的影响,而这种影响是间歇的,这种间歇式的作用会导致随机轨道模型所预报的离散相的湍流脉动小于真实值。
改进随机轨道模型则是把两相之间的湍流相互作用作为一个连续过程考虑。将改进随机轨道模型与常用的随机轨道模型进行对比,改进模型是从“连续相对离散相的湍流作用”和“离散相的经历效应”两方面来建立方程,给出了离散相湍动能或雷诺应力的拉格朗日方程,“随机力”并没有放在离散相的速度方程而是放在发展空间位置方程中。通过直接随机方法或Fourier级数方法对连续相脉动速度进行描述,能有效模拟两相流动中离散相的湍流弥散。该改进模型具有计算量小、易于得到合理的统计结果和易于考虑离散相入口湍流脉动状况等特点,不仅改善了原随机轨道模型低估离散相脉动量的缺点,还增强了离散相的湍流扩散和计算颗粒的位置随机性,使得离散相易于弥散到整个流场,只需要很少的计算颗粒就可以得到合理的离散相湍动能分布,还能使落入控制体内的轨道上的任何一点都参与统计计算,减少计算颗粒数,从而使统计曲线更加光滑。
离散相速度PDF模型在模拟离散相湍流扩散时比常用的随机轨道方法计算量小,统计结果的光滑性和精度更优,新位置的离散相速度计算更方便、精确。湍流离散相浓度模型虽然对直管和受限射流等气固两相流动在湍流边界层内的流动模拟是成功的,但在模拟复杂流固两相流场时还需进一步研究改善。且由于PDF方程闭合和求解的困难,离散相PDF模型常用于简单流动场合。
根据Prandtl湍流混合长理论的离散相湍流浓度模型考虑了离散相输送是连续相湍流卷吸效应和离散相自身湍动的相互作用。但由于湍流模化理论的限制,未能很好地模拟离散相的弥散特征,说明该模型存在一定范围的适用性和局限性,在复杂气固两相流场的模拟还需进一步研究改善。
对于流固两相流中稀疏离散相的复杂运动规律的描述,从它们的发展历程来看,主要是考虑“连续相对离散相的湍流作用”和“离散相的经历效应”两方面来建立方程,即提出了既定轨道模型、随机轨道模型、改进随机轨道模型等模型,因而基于常用随机轨道模型是对连续相脉动速度进行随机处理,改进随机轨道模型是对离散相脉动速度进行随机处理,因而对离散相的合力用随机Fourier级数进行描述,可发展为一种新的随机轨道模型,从而能够充分表达连续相产生的涡流对离散相的湍流作用和离散相反过来对连续相的影响。
另外流固两相流中稀疏离散相与连续相之间相互作用过程是绝对的,不论采用何种随机处理方法,与两相流的实际都会存在差异,因而可考虑两相耦合的方法,即离散相跟随连续相运动和交叉轨迹运动的耦合,连续相和离散相运动的耦合,来建立两相流的全耦合振动动力学模型。进而深入分析离散相种类、数量以及物理参数等各个影响因素对离散相动态特征的影响规律,并对离散相沿各个方向的体积浓度分布、速度分布以及轨迹等情况进行分析研究,才能全面、系统地描述流固两相流中稀疏离散相的运动特征,为实际工程应用提供理论支撑。
符 号 说 明
A1,A2,A3——根据湍流脉动频谱所确定的频率ωi下的脉动幅值
C1ε,C2ε,Cμ——连续相湍流模型常数
CD——曳力系数
dp——离散相的直径
Gk——湍动能发生率
gi——i方向上的重力加速度分量
k ——连续相湍动动能
p ——连续相的压强
R1,R3,R5——正态分布的随机数
R2,R4,R6——(0,1)均匀分布的随机数
Rep——颗粒雷诺数
u′,v′,w′ ——连续相的轴向、径向、切向脉动速度分量
ui——连续相速度
ui′ ——连续相脉动速度矢量
up,vp,wp——离散相的轴向、径向、切向瞬时速度分量
upi——离散相速度
upi′——离散相脉动速度矢量
ε——连续相的动力黏度
ζ——Gaussian分布的随机数
μ ——连续相湍动动能耗散率
μeff——连续相的有效动力黏度
μt——连续相的湍流黏性系数
v——连续相动力黏度
ρ ——连续相的密度
ρp——离散相的密度
σε——连续相湍动动能耗散率Prandtl数
σk——连续相湍动动能Prandtl数
τf——连续相的湍流时间标尺
τint——连续相与离散相的相互作用时间
τrp——离散相松弛时间
下角标
f——连续相
i——三维坐标系下的3个方向
j——三维坐标系下i的任一确定的方向
p——离散相
[1] 刘大有. 二相流体动力学[M]. 北京:高等教育出版社,1993.
[2] GIDASPOW D. Multiphase flow and fluidization-continuum and kinetic theory descriptions[M]. New York:Academic Press,1994.
[3] PATIL D J,ANNALAND M V S,KUIPERS J A M. Critical comparison of hydrodynamic models for gas-solid fluidized beds—Part 1. Bubbling gas-solid fluidized beds operated with a jet[J]. Chemical Engineering Science,2005,60(1):52-72.
[4] DURST F,MILOIEVIC D,SCHONUNG B. Eulerian and lagrangian predictions of particulate two-phase flows:a numerical study[J]. Applied Mathematical Modelling,1984,8(2):101-115.
[5] GIDASPOW D. Hydrodynamics of fluidization and heat transfer:supercomputer modeling[J]. Applied Mechanics Reviews,1986,39(1):1-23
[6] MINIER J P,CHIBBARO S,POPE S B. Guidelines for the formulation of lagrangian stochastic models for particle simulations of single-phase and dispersed two-phase turbulent flows[J]. Physics of Fluidsm,2014,26(11):113-303.
[7] CHIBBARO S,MINIER J P. Stochastic modelling of polydisperse turbulent two-phase flows[J]. International Centre for Mechanical Sciences,2014,548:39-86.
[8] 陈彬,韩超,刘阁. 铜颗粒污染物对变压器油粘度的影响研究[J].北京航空航天大学学报,2015(11):1-8.
[9] 陈彬,韩超,刘阁. 变压器油中颗粒污染物的中红外光谱检测研究[J]. 光子学报,2016,45(5):0530002.
[10] 陈彬,刘阁,张贤明,等. HVAS涂层力学性能的T-S模糊辨识[J]. 计算力学学报,2012,29(3):458-463.
[11] 刘阁,陈彬,张贤明. 水击驻波场中乳化油液分散相颗粒的运动分析[J]. 应用力学学报,2012,29(2):120-126.
[12] 倪晋仁. 固液两相流基本理论及其最新应用[M]. 北京:科学出版社,1991.
[13] CROWE C T,SHARMA M P,STOCK D E. The particle-source-in cell (PSI-CELL) model for gas-droplet flow[J]. Fluids Engineering,1977,99(2):325-332.
[14] SMITH G P,CROSLEY D R. Quantitative laser-induced fluorescence in oh transition probabilities and the influence of energy transfer[J]. Symposium on Combustion,1981,18(1):1511-1520.
[15] GOSMAN A D,LOANNIDES E. Aspects of computer simulation of liquid fueled combustors[J]. Journal of Energy,1983,7(6):482-490.
[16] BERLEMONT A,DESJONQUERES P,GOUESBET G. Particle lagrangian simulation in turbulent flows[J]. International Journal of Multiphase Flow,1990,16(1):19-34.
[17] YUU S,YASUKOUCHI N,HIROSAWA Y,et al. Particle turbulent diffusion in a dust laden round jet[J]. AIChE Journal,1978,24:509-519.
[18] CARUYER C,MINIER J P,GUINGO M,et al. A stochastic model for particle deposition in turbulent flows and clogging effects[J]. Springer Singapore,2015,22(8):451-466.
[19] LAN X Y,ZHONG H B,GAO J S. CFD simulation on the gasification of asphalt water slurry in an entrained flow gasifier[J]. Petroleum Science,2014,11(2):308-317.
[20] MAHDAVIMANESH M,NOGHREHABADI A R,BEHBAHANINEJAD M,et al. Lagrangian particle tracking:model development[J]. Life Science Journal,2013,10(8s):34-41.
[21] 陈彬,刘阁. 化工管路系统的藕合振动主动控制研究[J].振动与冲击,2009,28(8):158-162.
[22] 陈彬,刘阁,张贤明. 真空压力对油水分离的影响研究[J]. 哈尔滨工程大学学报,2013,34(10):1339-1344.
[23] 张小兵,翁春生,金志明,等. 混合颗粒床中颗粒轨道模型及其数值模拟[J]. 工程力学,1998,15(2):129-137.
[24] 欧阳洁,李静海. 模拟气固两相流动非均匀结构的颗粒运动分解轨道模型[J]. 中国科学(B辑),1999,29(1):29-38.
[25] 汪靓,崔小朝,蔡明,等. 拉格朗日-雷诺应力模型在后台阶颗粒流中的运用[J]. 太原科技大学学报,2011,32(5):406-409.
[26] 查旭东,樊建人,郑友取,等. 采用欧拉和拉格朗日混合模型对浓相颗粒流的研究[J]. 动力工程学报,2000,20(5):884-891.
[27] 查普曼·考林. 非均匀气体的数学理论[M]. 北京:科学出版社,1990.
[28] 陈彬,刘阁. 液压控制阀的水击振动耦合模型研究[J]. 化工自动化及仪表,2008,35(6):55-59.
[29] 邵萌,王安麟,梁波,等. 三维流固两相流的颗粒群轨道柔性模型[J]. 上海交通大学学报,2004,21(6):790-794.
[30] 李国美,王跃社,孙虎,等. 节流器内液-固两相流固体颗粒冲蚀数值模拟[J]. 石油学报,2009,30(1):145-148.
[31] 李国美,王跃社,亢力强. 突扩圆管内液-固两相流固体颗粒运动特性的DPM数值模拟[J]. 工程热物理学报,2008,29(12):2061-2064.
[32] WANG X Y,XIAO Y H. Research of the gas-solid flow character based on the DEM method[J]. Journal of Thermal Science,2011,20(6):521-526.
[33] GERBER S,OEVERMANN M. A two dimensional Euler-Lagrangian model of wood gasification in a charcoal bed—PartⅠ:Model description and base scenario[J]. Fuel,2014,115(1):385-400.
[34] CHU K W,KUANG S B,YU A B,et al. Prediction of wear and its effect on the multiphase flow and separation performance of dense medium cyclone[J]. Minerals Engineering,2014,56(2):91-101.
[35] KRUGGEL-EMDEN H,OSCHMANN T. Numerical study of rope formation and dispersion of non-spherical particles during pneumatic conveying in a pipe bend[J]. Powder Technology,2014,268(1):219-236.
[36] DU M,ZHAO C S,ZHOU B,et al. DSMC prediction of particle behavior in gas-particle two-phase impinging streams[J]. Mathematical Problems in Engineering,2013(2):1-11.
[37] LUO K,JIN J,ZHENG Y Q,et al. Direct numerical simulation of particle dispersion in gas-solid compressible turbulent jets[J]. Chinese Journal of Chemical Engineering,2005,13(2):161-166.
[38] LUO K,JIN H H,FAN J R,et al. Large eddy simulation of the gas-particle turbulent wake flow[J]. Journal of Zhejiang University:Science,2004,5(1):106-110.
[39] LUO K,ZHENG Y Q,FAN J R,et al. Interaction between large-scale vortex structure and dispersed particles in a three dimensional mixing layer[J]. Chinese Journal of Chemical Engineering,2003,11(4):377-382.
[40] ZHA X D,FAN J R,SUN P,et al. Numerical simulation on dense gas-particle riser flow[J]. Journal of Zhejiang University,2000,1(1):29-38.
[41] BESBES S,HAJEM M E,AISSIA H B,et al. PIV measurements and Eulerian-Lagrangian simulations of the unsteady gas-liquid flow in a needle sparger rectangular bubble column[J]. Chemical Engineering Science,2015,126(14):560-572.
[42] 陈曦,葛少成,张忠温,等. 原煤暗道通风除尘特征参数的数值模拟及优化[J]. 环境工程学报,2015,9(1):269-274.
[43] 袁惠新,吕浪,殷伟伟,等. 不同入口形式的固液分离旋流器壁面磨损研究[J]. 化工进展,2015,34(10):3583-3588.
[44] 余徽,陈思含,魏文韫,等. 应用随机轨道模型研究湍流扩散对气液交叉流脱除PM2.5的影响[J]. 四川大学学报(工程科学版),2015,47(5):178-184.
[45] 唐婵,张靖周. 含微小颗粒气流横掠圆管束表面的沉积特性[J]. 中南大学学报(自然科学版),2015,46(12):4679-4685.
[46] 陆耀军,周力行,沈熊. 油滴在液-液旋流分离中的随机轨道数值模拟[J]. 力学学报,1999,31(5):513-520.
[47] 陈彬,刘阁,张贤明. 温度对油水分离的影响研究[J]. 机械科学与技术,2014,33(2):233-238
[48] 袁惠新,殷伟伟,黄津,等. 固液分离旋流器壁面磨损的数值模拟[J]. 化工进展,2015,34(3):664-670
[49] 王志斌,陈文梅,褚良银,等. 旋流分离器中固体颗粒随机轨道的数值模拟及分离特性分析[J]. 机械工程学报,2006,42(6):34-39.
[50] 周大伟,向晓东. 环缝内衬固液分离耐磨旋流器磨损的数值模拟[J]. 化工进展,2016,35(2):397-402.
[51] YAKHOT V,ORSZAG S A. Renormalization group analysis of turbulence. I. Basic theory[J]. Journal of Scientific Computing,1986,1(1):3-51.
[52] 张志峰,刘洋,蔡体敏. 随机颗粒轨道模型在长尾喷管发动机流场计算中的应用[J]. 固体火箭技术,2007,30(5):376-380.
[53] 刘静,徐旭. 随机轨道模型在喷管两相流计算中的应用[J]. 固体火箭技术,2006,29(5):333-336,353.
[54] 陈彬,刘阁,张贤明. 运行时间对油水真空分离的影响[J]. 计算物理,2015,32(5):579-585.
[55] ZHANG Z,CHENG X W,ZHENG Y G,et al. Numerical simulation of erosion-corrosion in the liquid solid two-phase flow[J]. ChineseJournal of Chemical Engineering,2000,8(4):347-355.
[56] XU Y G,LIU M Y,TANG C. Three-dimensional CFD-VOF-DPM simulations of effects of low-holdup particles on single-nozzle bubbling behavior in gas-liquid-solid systems[J]. Chemical Engineering Journal,2013,222(8):292-306.
[57] 覃先云,肖庆麟,周枫林,等. 扫路车吸嘴气固两相流仿真分析及其设计改进[J]. 应用力学学报,2016,33(1):73-79.
[58] SHAO J R,LI H Q,LIU G R,et al. An improved SPH method for modeling liquid sloshing dynamics[J]. Computers & Structures,2012,100(6):18-26.
[59] RAMNAUJACHARI V,NATARAJAN R. Computation of particle-laden turbulent gas jet flows employing the stochastic separated flow approach[J]. Defense Science Journal,2013,42(4):273-280.
[60] 樊建人,赵华,岑可法. 气固两相流动的湍流脉动扩散数学模型及其应用[J]. 应用力学学报,1990,5(1):50-55.
[61] 李嘉,张永泽,李克峰. 剪切紊流中颗粒运动的数学模型和实验研究[J]. 水利学报,1998(6):8-14.
[62] 徐江荣. 两相流颗粒轨道模型的特征频率-频谱方法[J]. 杭州电子工业学院学报,2000(4):46-50.
[63] 张会强,陈昌麒,柳开瑞. 改进的随机轨道模型[J]. 工程热物理学报,1999,20(5):647-651.
[64] 张会强,陈昌麒,柳启瑞. 用改进的随机轨道模型数值模拟突扩液固两相流动[J]. 工程热物理学报,2000,21(5):652-656.
[65] 徐江荣,周志军,张巍,等. 颗粒Reynolds正应力轨道模型及后台阶两相流动数值模拟[J]. 计算物理,2004,21(6):538-542.
[66] 李昭祥,徐江荣. 随机轨道模型中颗粒湍流量模拟方法[J]. 杭州电子工业学院学报,2004(3):11-14
[67] 张健,周力行. 气固两相流中颗粒轨道运动方程的一组分析解[J].燃烧科学与技术,2000,6(3):226-229.
[68] STEPHEN B. Self-conditioned fields for large-eddy simulations of turbulent flows[J]. Journal of Fluid Mechanics,2010,652(4):139-169.
[69] MINIER J P,PEIRANO E. The PDF approach to turbulent polydispersed two-phase flows[J]. Physics Reports,2001,352(1-3):1-124.
[70] WANG L P,STOCK D E. Stochastic trajectory models for turbulent diffusion:Monte Carlo process versus Markov chains[J]. Atmosphere Environment,1992,26(9):1599-1607.
[71] 郭国庆,徐江荣. 颗粒速度概率密度分布轨道模型及数值模拟[J].杭州电子科技大学学报,2006(2):74-77.
[72] XU J R,WANG L. Two-order moment trajectory model of two-phase turbulence flow based on particle PDF transport equation[J]. Applied Mechanics and Materials,2014,668/669:318-321.
[73] 顾璠,许晋源. 气固两相流场的湍流颗粒浓度理论模型[J]. 应用力学学报,1994,11(4):11-18.
[74] 徐进,葛满初. 气固两相流动的数值计算[J]. 工程热物理学报,1998,19(2):233-236.
[75] 欧阳洁,李静海. 确定性颗粒轨道模型在流化床模拟中的研究进展[J]. 化工学报,2004,55(10):1581-1592.
[76] CHEN J K,WANG Y S,LI X F,et al. Erosion prediction of liquid-particle two-phase flow in pipeline elbows via CFD-DEM coupling method[J]. Powder Technology,2015,275(5):182-187.
[77] 欧阳洁,李静海,崔俊芝. 颗粒轨道模型中相间耦合关系及曳力计算的研究[J]. 动力工程,2004,24(6):857-862.
[78] WEN C Y,YU Y M. Mechanics of fluidization[J]. Chem. Eng. Prog.:Symp. Ser.,1996,62:100-111.
Progress in the dilute discrete model of fluid-solid two phase flow
CHEN Bin,YAN Huan,LIU Ge,HAN Chao
(Engineering Research Centre for Waste Oil Recovery Technology and Equipment,Chongqing Technology and Business University,Chongqing 400067,China)
The dilute particle of fluid-solid two phase flow widely exists in practical application of chemical engineering,storage and transportation,separation etc. The description of the complex turbulent motion is one of the research hotspot and difficulty of two phase flow. The growing process of the dilute discrete phase model was reviewed in this paper,which from the theoretical basis,the modeling process,the numerical simulation method and the application of several aspects of the discrete phase model,the discrete phase model,the stochastic trajectory model,the improved stochastic trajectory model has carried on the detailed elaboration. The interaction coupling relationship between discrete and fluid phase was theoretically analyzed,and the corresponding model was evaluated. Then,the paper pointed out that the present problems and the future development direction of the discrete phase orbit model. This paper puts forward an advanced stochastic trajectory model which based on random Fourier series describing the discrete phase resultant force to describe the motion law of discrete phase to deal with fluid phase fluctuation velocity randomly in the future,so as to better describe the motion law of discrete phase,at the same time considering of the coupling two phase,to establish full coupling vibration dynamic model of two phase flow,and describe the movementcharacteristics of discrete phase of fluid-solid in the two phase flow comprehensively andsystematically,providing theoretical basis for the in-depth development of the dilute discrete model in fluid-solid two phase flow.
fluid-solid two phase flow;discrete phase model;stochastic trajectory model;sparse discrete phase;two phase coupling
TQ 018;TQ 028.4
A
1000-6613(2016)11-3400-13
10.16085/j.issn.1000-6613.2016.11.003
2015-12-22;修改稿日期:2016-06-26。
国家自然科学基金项目(51375516)。
及联系人:陈彬(1972—),男,教授,博士,主要从事油液污染控制技术方面的研究。E-mail hustchb@163.com。
