一种改进的多相交错buck变换器的滑模变结构控制器设计
2016-11-12夏建生赵进全
夏建生 赵进全 邢 玲
(西安交通大学电气工程学院,西安 710049)
一种改进的多相交错buck变换器的滑模变结构控制器设计
夏建生 赵进全 邢 玲
(西安交通大学电气工程学院,西安 710049)
滑模变结构控制主要应用于线性或非线性、集中参数及非集中参数、集中控制及离散控制等,以其鲁棒性强,稳态范围宽,动态响应快等特点而引入到开关电源控制中。本文对低压大电流DC-DC变换器的主要拓扑结构-多相交错buck变换器进行了滑模算法分析,并根据它的特性,选择了适当的滑模面;在研究了滑模性能后,为进一步改善交错信号产生原理,对滑模面进行了改进,得到了可以自动交错的多相控制信号;当电感寄生参数DCR不均衡时,提出了占空比补偿的方式,从而改善了各相电感之间的电流平衡。通过仿真分析,得到很好的均流及动态特性。
滑模变结构控制;多相交错变换器;均流;DCR不均衡
电压调节模块(VRM),主要是为微处理器等电路提供高精度的电压和具有快速动态响应的供电电源。随着微处理技术的发展,微处理器的运行速度增加和集成密度增大,为了适应更高的速度和效率,微处理器的工作电压越来越低,VRM向着低电压、大电流、小体积、高效率、快速动态响应的方向发展。对于低输出电压的大负载电流的变换器,若采用单相buck拓扑,功率损失会很大,而且对器件的要求极其严格,所以往往采用多个系统并联或多相交错运行的buck变换器。这也是目前低压大电流非隔离变换器的主流拓扑结构。交错技术的关键问题是解决均流问题,要使各相电流相互均衡,增加系统可靠性。
滑模变结构控制(SMC)作为一种非线性控制技术,它与传统控制方法的区别在于控制的不连续性,无论系统参数是否固定,它可以根据系统状态,有目的的使系统按照要求的滑动模态来运动。所以,滑模变结构控制具有快速响应,动态性能好,具有很好的鲁棒性,对参数变化和扰动不灵敏,不需要系统在线辨识,硬件设计及实现简单等优点。
1 多相交错buck变换器
n相电路中,不同相的MOSFET的驱动信号错开 T/n的时间差,在同一时间各相相互作用,同步交错运行。多相交错buck变换器的设计需要解决其均流和控制信号交错等问题,其中最重要的就是均流问题,也就是保证各相之间的电感电流相等。
1.1 多相交错变换器模型
在变换器并联系统中,所有的控制信号是同步的,这样各个变换器的纹波噪声等信号相互叠加,成倍的增加了不利信号,使得系统性能降低;对于交错运行的变换器,控制信号频率相同,但相位会错开一定的角度,这个角度与并联的变化器个数有关,即φ=2π/n,这样不但可以减小纹波,降低了对器件的要求,大大提高了系统可行性。

图1 两相交错buck变化器拓扑结构
图1所示的两相buck变化器,Q1与Q2,Q3与Q4分别是两对加入死区的互补驱动信号,而Q1与 Q3信号的相位相差φ=2π/2=π,即控制信号相差180°,多相降压变换器模型可由下列方程表示为

1.2 多相buck变换器滑模面分析
理想多相交错变换器的状态方程为
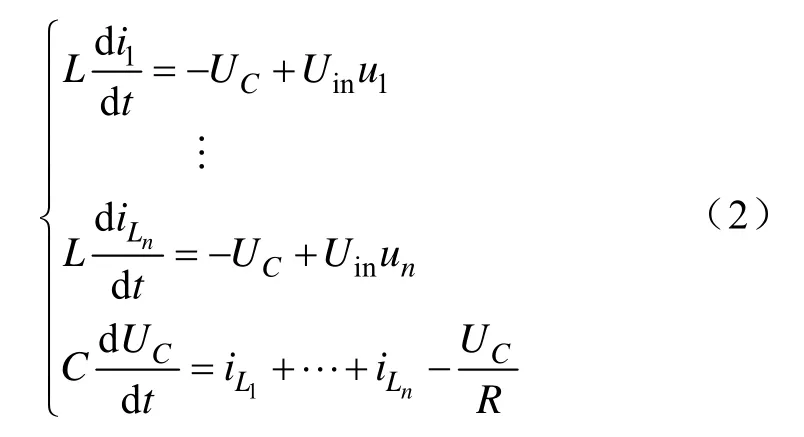
为保证对输出电压的控制,滑模面中加入了电压误差量,同时对于多相交错变换器最重要的目的是实现电流均衡,所以也引入了电感电流误差值。

式中,Uref是电压参考值;是输出电流参考值。
为了使电压输出稳态误差为零,同时保证电感电流的均流,在滑模面中加入电压误差和电流误差环节,所以得到下面的滑模面:
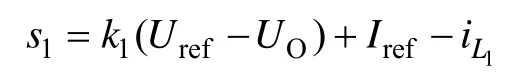
变换后得到

这样就可以得到包括输出电压误差及电感电流误差的滑模面,即
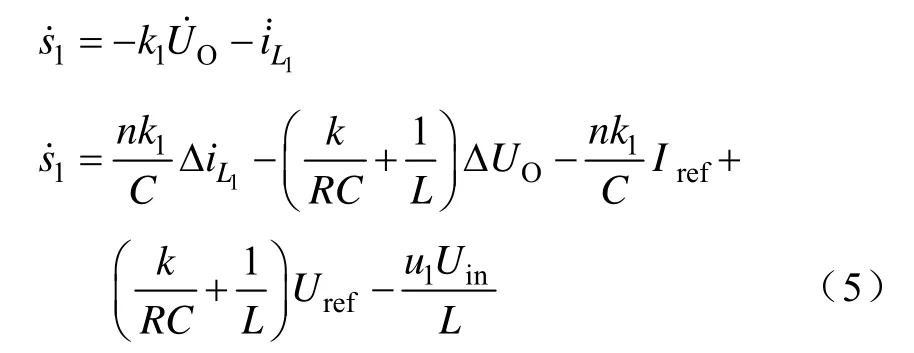
图2为滑模控制的实现过程框图。每一项的控制信号都有输出电压误差,电感电流误差经过滞环控制获得。
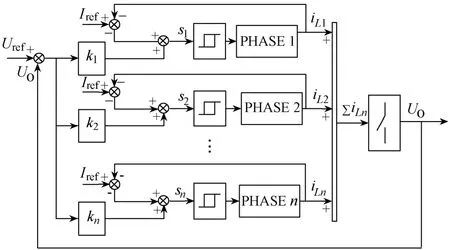
图2 滑模控制结构图
为了保证滑模面存在条件,需要满足李雅普诺夫函数的条件,即可得到
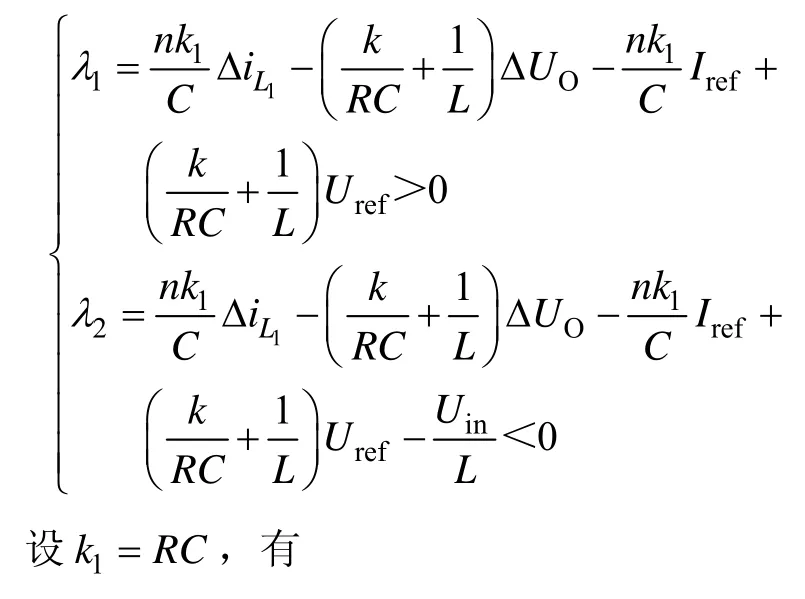
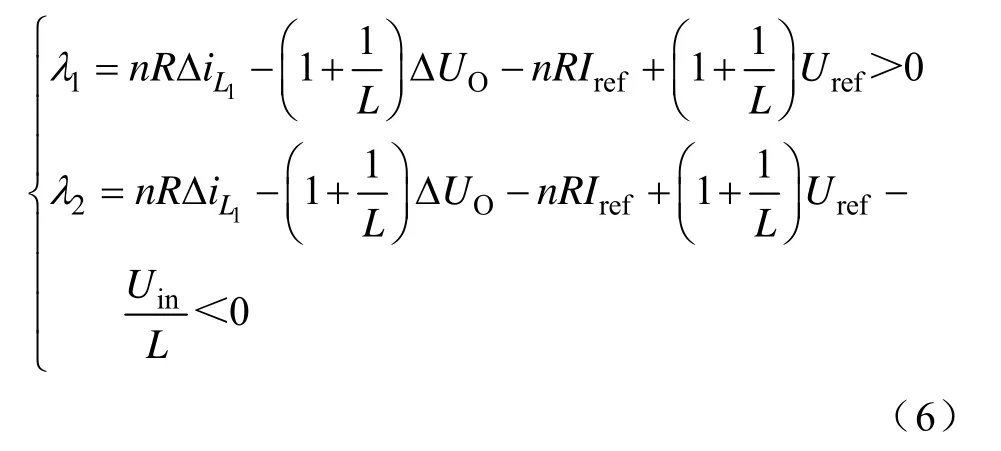
由式(6)可获得其相滑模面的情况,图3显示了滑模域及相轨迹在相平面上的位置。
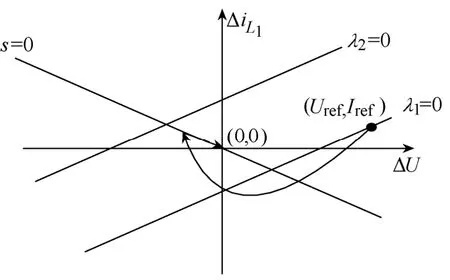
图3 滑模面相轨迹图形
初始状态位于直线λ1=0上,系统运行后,状态轨迹第一次与直线λ1=0相交,然后进入滑模域之内,与s1=0相交,在滑模面上滑动,直至稳态。
图4是相轨迹的稳态示意图,滑模面s1通过滞环控制得到一个滞环窗口,稳定状态时,实际上就是电感电流的纹波。
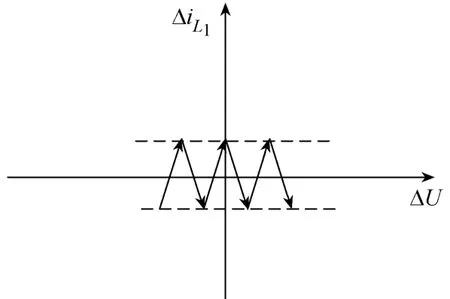
图4 稳态时的状态
当s1的宽度为2δ时,进入稳定状态后,ΔUO就是输出电压纹波,由于所以且其数量级通常在以下,则滑模面中的电压误差的影响可以忽略。
如图5所示,此时滑模面滞环宽度2δ与电感电流的波动范围近似相等。
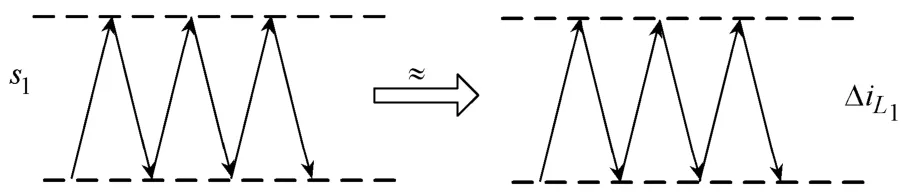
图5 滞环宽度
由此可以推出稳态条件下的开关频率:
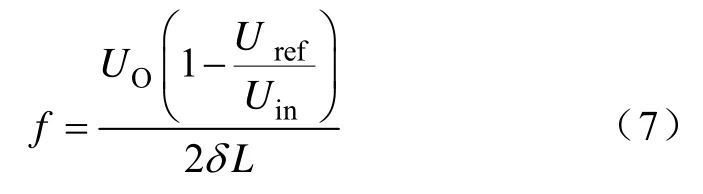
当n相变换器的各路控制信号相同时,其输出电压误差相互叠加,增大了电压纹波。
若采用交错信号进行控制,可以得到交错的纹波,大大减小了电压纹波。
1.3 滑模面的改进
当考虑电感寄生参数DCR后,为了解决交错运行的均流问题,将滑模变结构控制技术引入。
控制率

为满足滑模控制的存在性和可达性条件,则
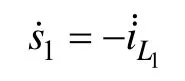
取s1的滞环宽度为Δ,得到开关频率值为

图6表示了n相交错变换器滑模变结构控制的实现过程。
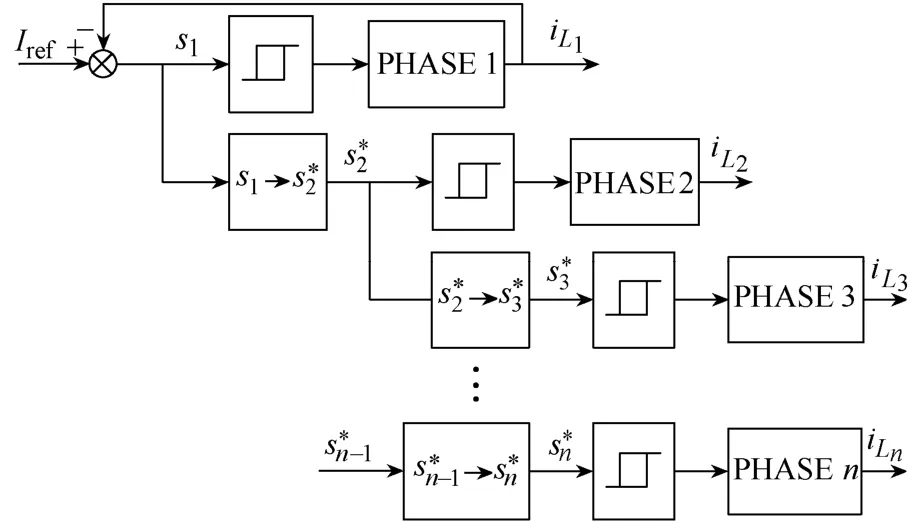
图6 n相交错变换器滑模变结构控制结构图
为了得到交错的控制信号,令
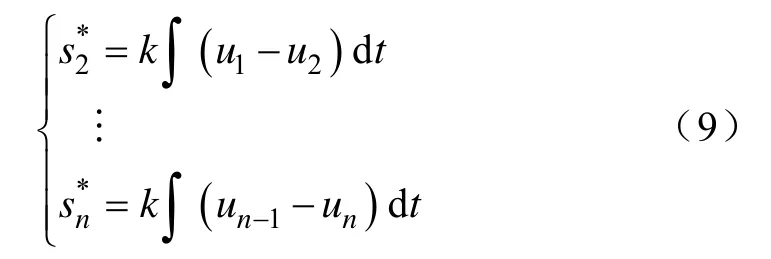
其积分形式为

相位角度差为

k值可以由此得到,即
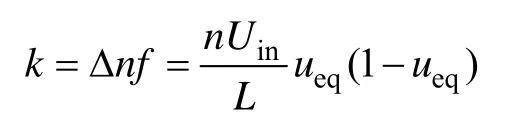
为了满足交错相位,需要确保:
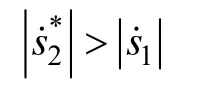
则
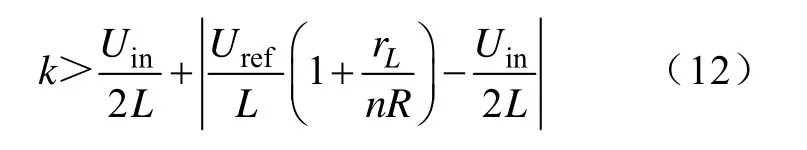
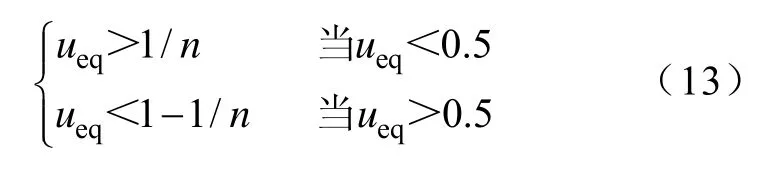
这是交错成立的条件,多相交错电路滑模控制器的设计根据占空比选择适当的多相交错相数。
1.4 DCR不均衡的滑模控制
电感存在着寄生参数DCR,当DCR差异较大时,导致多相交错电路的电流不平衡,出现单相电流下降,输出电压降低,对器件产生损害,影响性能,可能导致系统无法正常工作。
根据前面所设计的滑模面,各相的占空比是相同的,没有差异,但是当各相的DCR不同时,无法达到电流的平均值,电流无法均衡。如图7所示,DCR较大的相,平均电流下降。
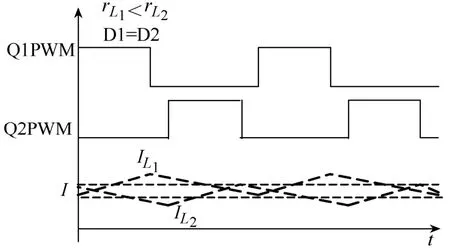
图7 电感电流不平衡时的电流
当第一相和第二相的占空比不同,d1<d2。由于存在一个区域使得s*2<0,在运算过程中会逐渐积累饱和,无法得到Tφ,如图8所示。
对此,DCR不均衡条件下滑模控制设计如下:
设交错电路第一相的电感寄生电阻为 rL1,第二相的电感寄生电阻为,并且
则有
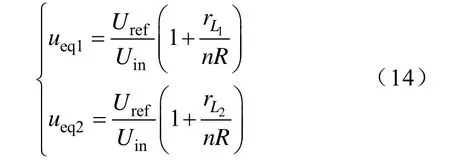

图8 电流不均衡时的控制信号
保证各相的频率相等,即

ΔT1是需要补偿的额外占空比对应的导通时间。此时相位差Tφ不会发生变化。
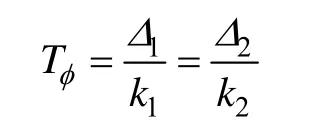
当负载发生变化时,由公式可以看出R发生变化,保持Δ不变,从而ueq变化,最终导致f变化,这样必然导致Tφ变化,即各相之间的相位差改变,如果不作调整,电感电流不能够完全叠加,而是带有各相纹波的电流,如果根据当前条件对k进行更改调节,这种控制方式称为自适应方式控制,自适应的控制有利于各相电流之间的均衡和动态性能。
2 仿真分析
由此计算出:

当滑模面选择s1=k1ΔU+ΔiL1时,RC=5×10-5,则k1=RC=5×10-5。
进行仿真分析,图9为稳定状态相轨迹图。

图9 稳定状态相轨迹图
动态时,负载电流由变化为:40A—20A—40A,得到图10的动态相轨迹图。
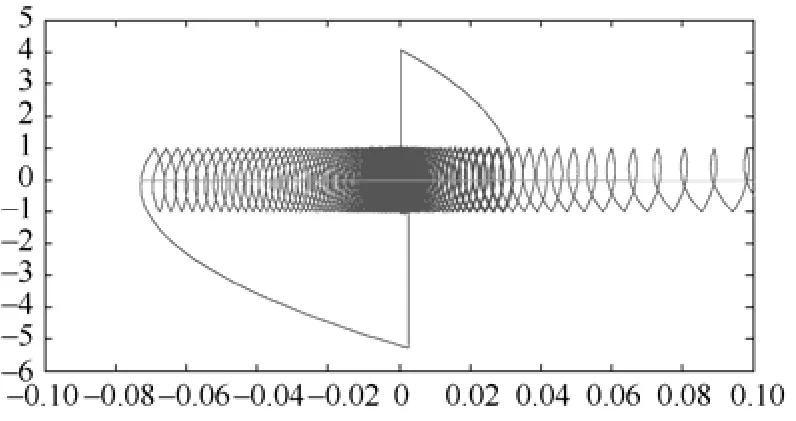
图10 动态时的相轨迹图
当选用改进滑模面s1=Iref-iL1,DCR均衡时进行仿真分析,系数k的设计采用自适应方式选择,即k随着负载参数的变化而变化,四相电路的电感电流起动状态如图11所示,四相电流具有不同的起动状态,每一相的交错相位由前一相通过滑模控制得到,因此各相的动态过程具有差异,各相具有很好的交错性能。
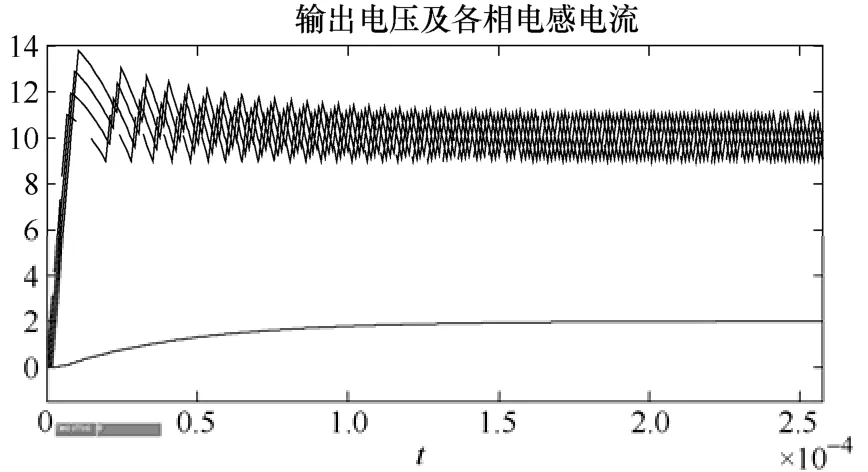
图11 起始状态的输出电压及各相电流波形
当负载在半载和满载之间变化时,采用自适应控制,动态特性仿真结果如图12所示,负载降低时,电压升高83mV,动态调整时间为350μs左右;负载增加时,输出电压跌落为 90mV,动态调整时间是200μs。
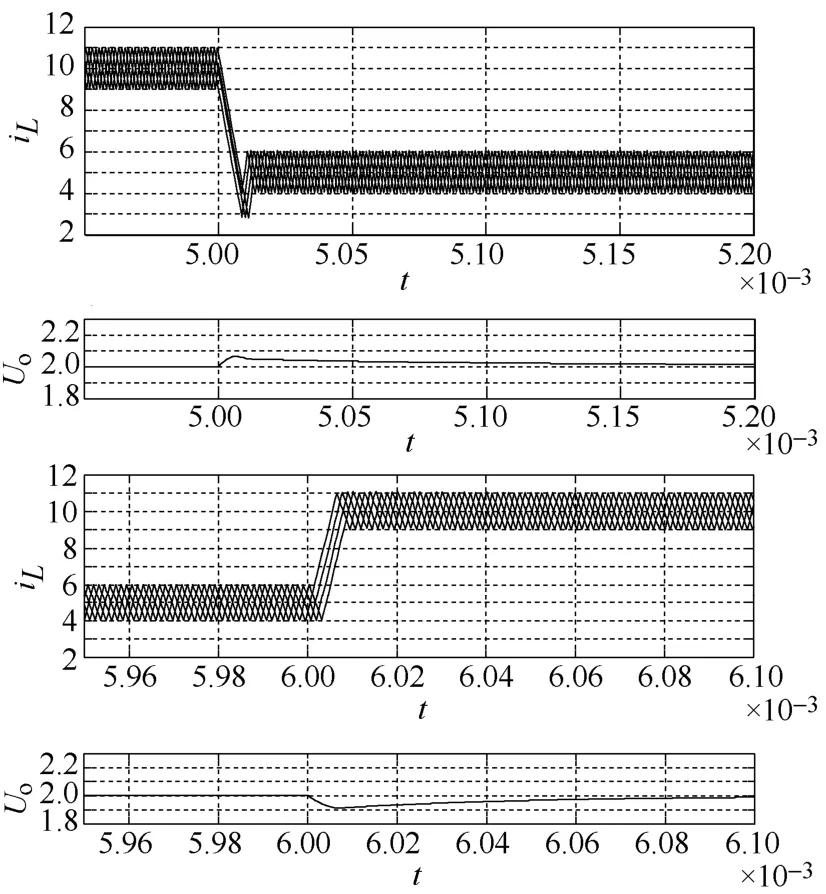
图12 动态条件下的电感电流及输出电压
可以看出,采用了自适应控制之后,无论动态还是稳态过程的各相电感电流波形之间的相位差都可以自动匹配,均流效果很好,动态相应较快。
当DCR不均衡,选择 rL4=0.02Ω,这样导致了各项电流的不均衡,第四相的电流下跌,输出电压同时下跌,如图13所示,电感电流不能平衡,在实际应用中容易引起严重的结果。

图13 电感电阻不均衡时的电流波形
在不均衡的相内加入占空比补偿来改善性能,图14表示了第四相的原始占空比和在占空比补偿
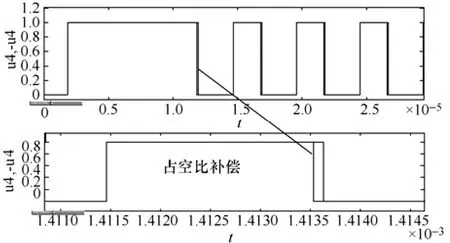
图14 占空比补偿
后所得到的控制信号波形图,改变了占空比后,交错信号没有发生变化,各相相位差不变。这样就得到了新的电感电流交错过程,图15为补偿后所得到的电感电流,第四相电流用实线表示,可见,这时候的第四相电流几乎与其他相相同,虽然略有差异,但补偿效果很好。

图15 引入占空比补偿后的各相电感电流波形
3 结论
多相交错buck变换器具有其特有的设计要求,为实现各相电感电流之间的均衡,选择了具有电压误差和电感电流误差项做为滑模面,这种滑模面不容易产生交错控制信号,但对于数字控制方式是可行的。通过改进滑模面,得到了n相交错控制信号,实现了模控制,这种控制方式效果很好,当负载变化,动态响应选用自适应滑模系数;当电感寄生参数DCR不同时,本文提出了一种占空比补偿方式,利用滑模控制所产生的交错信号对不均衡相进行占空比补偿即可,得到较好的动态性能和均流效果。
[1]高为炳.变结构控制的理论及设计方法[M].北京:科学出版社, 1996.
[2]刘金琨, 孙富春.滑模变结构控制理论及其算法研究与进展[J].控制理论与应用, 2007, 24(3): 407-418.
[3]Ni Y, Xu Jp.Study of global sliding mode controled switching DC-DC converters[C]//China: IEEE International Conference on Industrial Technology, 2008: 1-5.
[4]Meng Shi.Design and analysis of multiphase DC-DC converters with coupled inductors[D].Texas A&M University, Master of science, 2007.
[5]裴云庆, 杨旭, 王兆安.开关稳压电源的设计及应用[M].北京: 机械工业出版社, 2010.
[6]Al-Hosani K, Utkin VI.Multiphase power boost converters with sliding mode[C]//2009 IEEE CONTROL APPLICATIONS CCA & INTELLIGENT CONTROL (ISIC), VOLS 1-3, 2009: 1541-1544.
[7]许飞, 马皓, 何湘宁.电流型交流功率放大器离散衰减变速趋近律控制[J].电工技术学报, 2008, 23(5): 75-80.
[8]张翔, 王德石, 李景熹.滑模控制器趋近律仿真研究[J].微处理机, 2008(1): 80-81.
[9]倪雨, 许建平.准滑模控制开关变换器分析[J].中国电机工程学报, 2008, 28(21): 1-6.
[10]李运德,张淼.无刷直流电机的指数趋近律滑模变结构控制[J].电机与控制应用,2011,38(3):32-35.
[11]张昌凡, 何静.滑模变结构的智能控制理论与应用研究[M].北京: 科学出版社, 2005.
夏建生(1955-),副教授,研究方向:控制工程及测控技术。
The Improved Design of the Sliding-mode Variable Structure Controller for the Multi-phase Staggered Interleaved Buck Converter
Xia Jiansheng Zhao Jinquan Xing Ling
(School of Electrical Engineering,Xi'an Jiaotong University,Xi'an 710049)
Sliding mode control is mainly used in linear or nonliner,certain or uncertain,lumped parameters or nonlumped parameter.It has some advantage such as its good robustness,widely steady-state range,and fast dynamic response.SMC had began to apply in switching mode power supply.In this paper the sliding mode controlled VRM is researched and analyzed about SMC of the VRM topology multi-phase buck converter.According to its own character,a proper sliding mode face is selected,and it current sharing and dynamic response is researched.When the DCRs of each phase is not equal,a new control method based on duty cycle compensation is discussed,and its current sharing is available.At last,Simulation and experiment is also done to verify the algorithm.
sliding mode control;multi-phase buck converter;current sharing;DCRs not equal
