基于压缩感知的MIMO-OFDM系统的信道估计*

杨　亮，齐丽娜

（南京邮电大学 通信与信息工程学院，江苏 南京 210003）

基于压缩感知的MIMO-OFDM系统的信道估计*

杨亮，齐丽娜

（南京邮电大学 通信与信息工程学院，江苏 南京 210003）

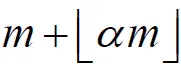
压缩感 知；信道估计；多输入多输出；正交频分复用；可扩展正交匹配追踪

0　引 言

正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）技术具有有效抵抗多径干扰、频率利用高和窄带干扰的特点［1］。多输入多输出（Multiple-Input Multiple-Output，MIMO）技术能有效改善无线通信系统的信道容量，在不增加天线发射功率和带宽的情况下，可以提高频谱利用率，从而改善通信质量。因此，将MIMO与OFDM技术相结合，可以提高信道容量和利用率，能够有效抑制噪声和干扰。在接收端为了能够接收到高质量的信号，精确的信道估计对于系统的性能评估至关重要。

基于压缩感知［2-5］（Compressed Sensing，CS）的MIMO-OFDM系统信道估计方法，能够减少导频数量，从而提高系统的频谱利用率。文献［6］将正交匹配追踪（Orthogonal Matching Pursuit，OMP）算法应用于MIMO-OFDM系统中的信道估计，提高了频谱利用率，但该算法是在忽略噪声的情况下进行的。文献［7］将OMP算法应用于OFDM系统中，对时域信道脉冲响应进行估计。和传统的信道估计算法相比，能够利用较少的导频信号来获得较好的信道估计性能，但该算法的复杂度较高，也没有应用到MIMO系统中。本文在以上算法的研究基础上，针对OMP算法存在的不足之处，提出了一种基于可扩展的正交匹配追踪算法（Extended Orthogonal Matching Pursuit，OMPα）的MIMO-OFDM系统的信道估计，其中α为扩展因子，α∈［0,1］。该算法在原有的OMP算法基础上，通过适当更改迭代次数，提高了信号重构概率和精度，同时进一步提高了信道估计性能。

1　MIMO-OFDM系统

假设在MIMO-OFDM系统中发送端的发射天线数为Nt，接收端的接收天线数为NR，子载波数为N，将发送端发送的数据分为Nt个不同的数据块。于是，第i根发射天线与第j根接收天线之间的信道冲激响应为：

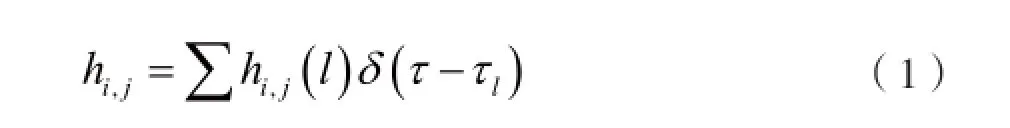
式中，τl和hi,j（l）分别为第l径的时延和复增益。MIMO-OFDM系统的原理框图，如图1所示。

图1　MIMO-OFDM系统原理

在发送端，数据源经时空编码和多载波调制后，插入循环前缀（CP），信号的最大时延扩展要求小于CP的长度，以消除符号间干扰（ISI）和载波间干扰（ICI），最后经天线发射出去。假设在一个OFDM符号的持续时间内，信道参数是恒定的，则在接收端，信号经同步去掉CP以及FFT变换后，可表示为：

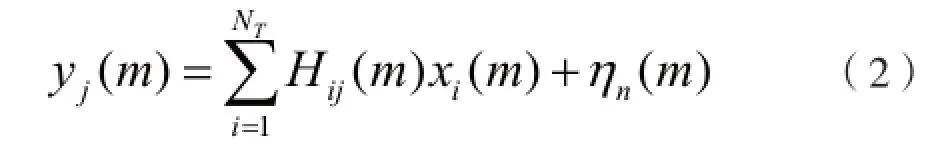
其中，xi（m）,yj（m）（i=1,2,…,NT；m=0,1,…,L-1）分别为第j根发送天线和第j根接收天线在第m个子载波上的OFDM符号；ηn（m）为均值为零、方差为的高斯白噪声。Hij（m）为第i根发送天线和第j根接收天线在第k个载波上的频域冲激响应：

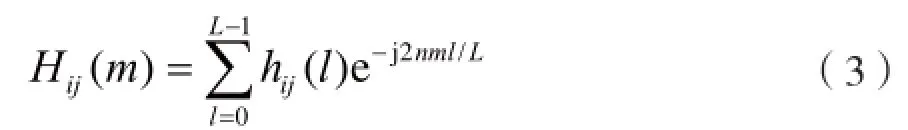
假设MIMO-OFDM系统选取P个导频符号，分别位于子载波m1,m2,…,mp上，则接收端第j根接收天线接收到的导频信号为：

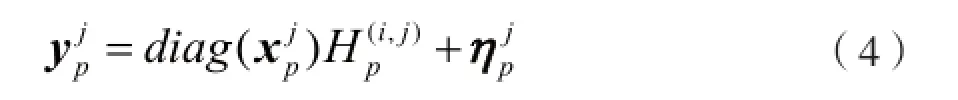
则式（4）可以表示为：

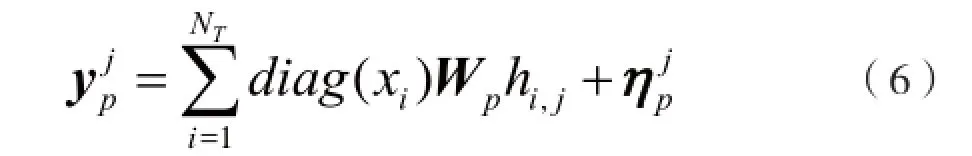
MIMO-OFDM系统的信道估计，即利用接收信号y和Φ来重构h。无线信道冲激响应具有稀疏性特点，基于这一特点，压缩感知（CS）理论起着重要的作用。文献［8-9］将压缩感知算法应用到信道估计中，与传统的信道估计算法相比，具有更高的精度和更低的复杂度，且减少了导频个数，提高了信道估计的性能。

2　压缩感知理论

压缩感知也被称为稀疏采样，对于稀疏信号或者可压缩信号，压缩感知可以以远小于Nyquist采样速率对信号进行采样，且能够利用少量的观测值精确重构出原始信号。其基本模型如图2所示。

图2　压缩感知基本模型

对一长度为N的离散实值信号x∈RN，稀疏度为K（即含有K个非零元素，其他N-K个元素都为零），X的观测值可以由观测矩阵ΦM×N（M＜N）获得：

式中，η为噪声，M≥K・lg N，观测矩阵Φ满足有限等距性质（Restricted Isometry Property，简称RIP）［10］。然而，式（9）是一个欠定方程，即方程未知数的个数多于方程组的个数，x的解不唯一。因此，如何从测量信号y精确地重构原始信号x是实现压缩感知的关键。对式（9）可以采用l1范数［11］来求解：

在最小l1范数下的最优化问题称为基追踪（Basic Pursuit，BP）［12］算法，而BP算法具有运算复杂度高而难以实现的特点。另一类运算量小且易于实现稀疏信号重构的是基于贪婪迭代算法［13-14］，如匹配追踪（Matching Pursuits，MP）算法、OMP算法。本文应用了可扩展的正交匹配追踪OMPα算法，α为扩展因子α∈［0,1］，提高了信号重构的精度、概率和信道估计的性能。

3　信道估计

3.1基于改进的正交匹配追踪算法信道估计

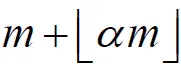
基于OMPα算法的信道估计步骤如 下：

（1）输入：y,Φ，m；

（2）初始 化：设定残差的初始值r0=y，Λ0=0，（Λt表示t次迭代的索引集合），初始迭代次数t=0；

（3）更新迭代次数t=t+1；

（4）计算余量rt-1与Φ的每一列的内积，选择内积最大值对应的索引值，即λt，有：

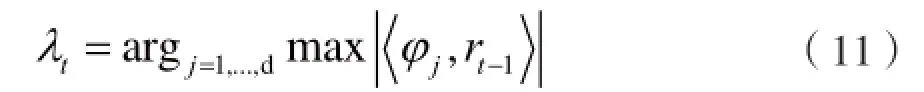
其中λt表示第t次迭代找到的索引（列序号）；

（5）更新索引值集合Λt=Λt-1∪｛λt｝，更新支撑集ΦΛt；

（6）通过最小二乘法LS获取最佳的t项解：

（8）输出x的稀疏逼近信号xt，即。在基于残差rt-1选择候选原子φj时，把测量矩阵分成两组Φ=［ΦI,ΦIc］。定义ΦI=｛φj：j∈I｝为正确的原子集，ΦIc=｛φj：j∈Ic｝为错误的原子集。选择正确的原子情况：

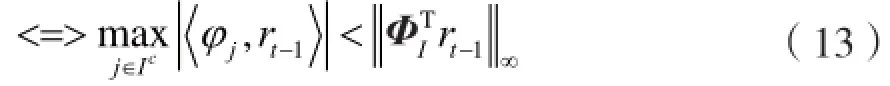
选择错误的原子情况：

OMPα算法运行的输出可以表示为：

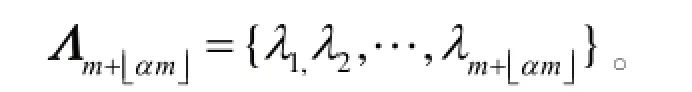
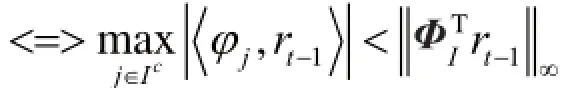
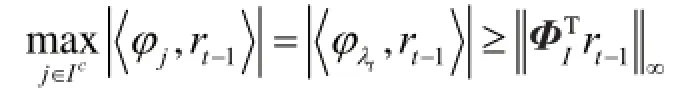
表示选择了错误的原子。下面使用以上两种选择集来说明OMPα算法重构信号是否重构成功。

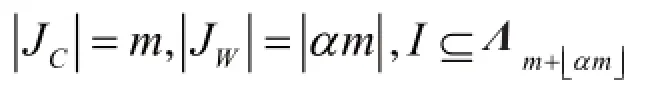
3.2OMPα算法性能推导

通过定义错误概率来说明正确概率。错误概率定义为：

由于左边的事件是右边事件的一个子集，所以其概率的上界对于给定的任何条件都是成立的。由以上推导，有：

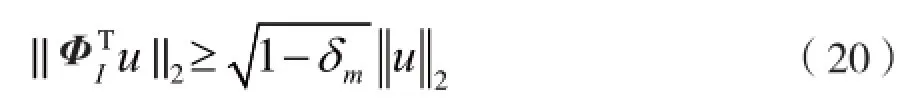
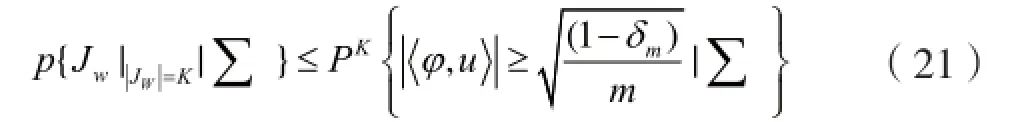
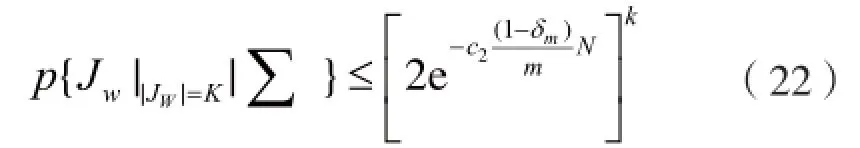
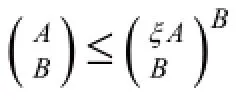
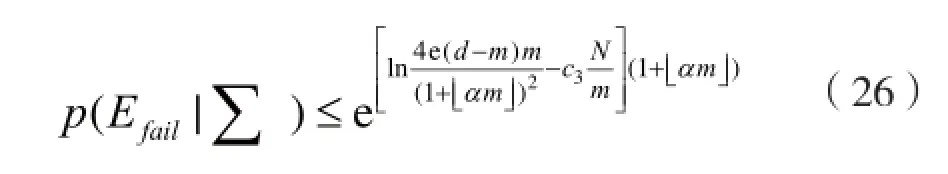
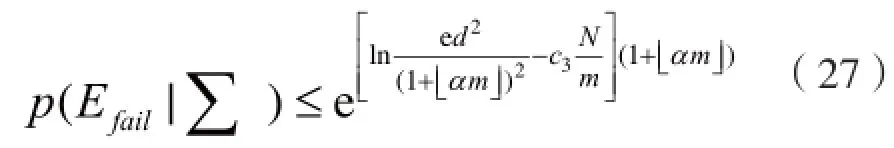
占主导地位的变量项吸收常数，因此有：

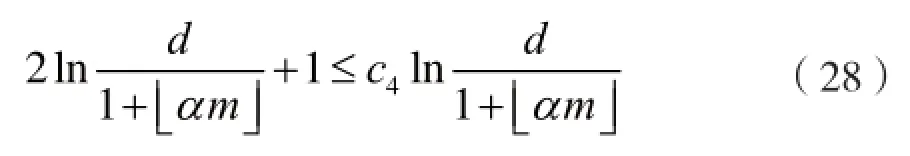
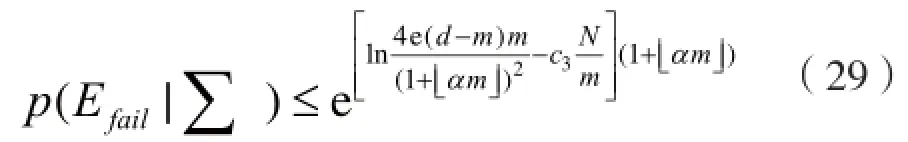
因此，OMPα的成功概率可以表示为：

通过适当增加c4和减少c3，有：

4　仿真及结果分析

为了说明OMPα算法在信号稀疏度不同情况下的重构精度和概率，以及比较OMPα算法和OMP算法、传统的LS算法在MIMO-OFDM系统中信道估计的不同性能，本文进行了如下仿真。图3比较了不同稀疏度下信号重构概率与扩展因子α之间的关系。稀疏度分别取值为68、76、84、92、100，进行1 000次试验，稀疏信号的维数为1 024。从图3中可以看出，对于选择不同的扩展因子α，不同稀疏度的信号精确重构的概率不同。

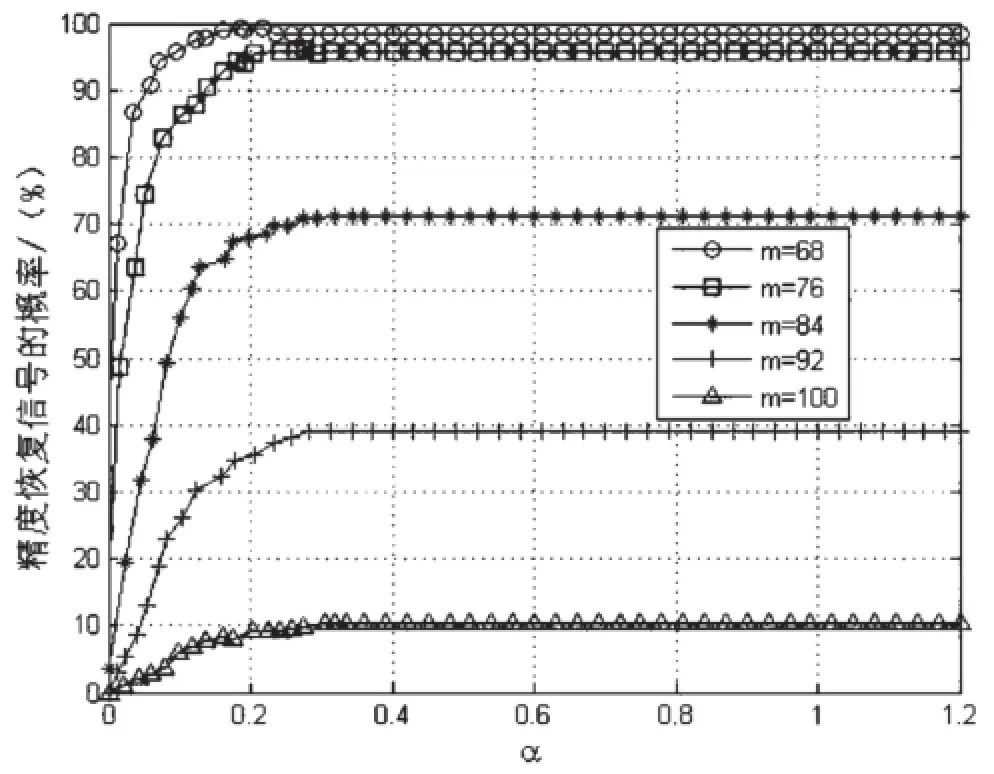
图3　不同稀疏度下信 号重构概率与扩展因子的关系

为了验证MIMO-OFDM系统中基于压缩感知的信道估计性能，将OMPα算法和OMP算法、传统的LS算法作为比较。系统仿真参数设置如下：发射天线数和接收天线数均为2，即2×2的MIMO-OFDM系统；子载波数为256；信道长度为50；信道多径数为6；调试方式为QPSK。图4为导频数相同的情况下，各算法在不同信噪比下的误码率比较图。仿真时，LS算法导频均匀放置，OMPα和OMP算法导频随机放置。由仿真图可以看出，LS算法的误码率最高，随 着信噪比的增大，误码率没有明显改善；而OMPα算法和OMP算法较LS算法具有更低的误码率，且OMPα算法比OMP算法的误码率更低。

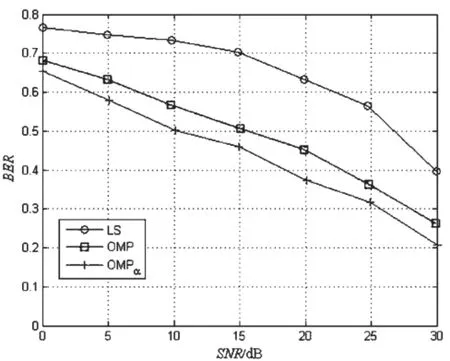
图4 不同信道估计方法的BER性能比较

图5给出了各算法的MSE曲线图。在导频数相同的情况下，随着信噪比的增大，OMPα算法和OMP算法的MSE相当，但比LS算法 要好得多。

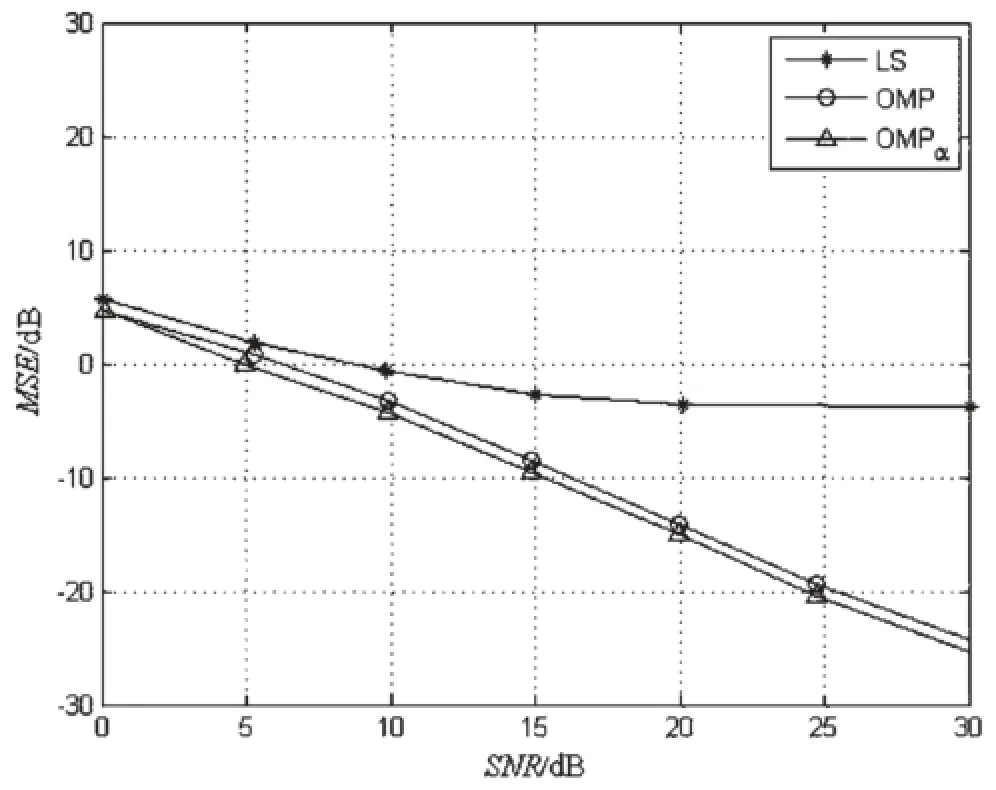
图5 不同信道估计方法的MSE性能比较

图6为不同导频数的各算法的MSE性能比较。OMPα算法和OMP算法的导频 数为32、48、64，LS算法的导频数分别为32、72和128。LS在导频数为32时，信道估计的性能很差，随着导频数的增加，性能有所改善，但是在牺牲传输数据资源的情况下获得的。而OMPα算法和OMP算法能够以少数的导频获得较好的 信道估计性能，且OMPα算法比OMP算法的性能更加优越，提高了系统的频谱利用率。

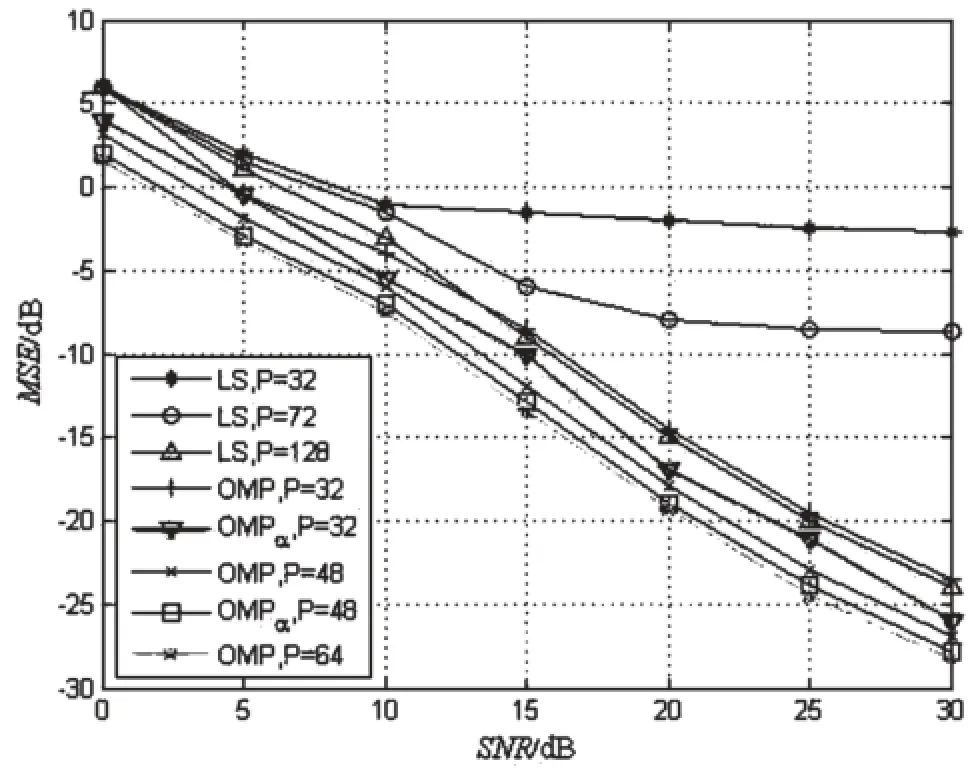
图6　不同导频数的各算法的MSE性能比较

5　结 语

本文主要根据MIMO-OFDM系统的信道特性，提出可扩展的正交匹配追踪算法，并将其应用到MIMO-OFDM系统的信道估计中。在正交匹配追踪算法的基础上，更改迭代次数来选择更加精确的匹配原子，从而实现信号的精确重构。仿真结果表明，可扩展的正交匹配追踪算法与传统的最小二乘法、正交匹配追踪算法相比，提高了信号的重构概率和精度，同时也提高了频谱资源的利用率和信道估计的性能。

［1］ ZHOU Y，WANG J，SAWAHASHI M.Downlink Transmission of Broadband OFCDM Systems-Part I:Hybrid Detection［J］.IEEE Transactions Communications，2005，53（04）:718-729.

［2］ Donoho D L.Compressed Sensing［J］.IEEE Transaction on Information Theory，2006，52（04）:1289-1306.

［3］ Candes E J.Compressive Sampling［A］//In Proceedings of the International Congress of Mathematics，Madrid［M］. Spain:the European Mathematical Society，2006: 1433-1452.

［4］ Bajwa W，Haupt J，Sayeed A.Compressing Channel Sensing:A New Approach to Estimating Sparse Multipath Channels［J］.Proceedings of the IEEE，2010，98（06）:1058-1076.

［5］ 石光明，刘丹华，高大化等.压缩感知理论及其研究进展［J］.电子学报，2009，37（05）:1070-1081. SHI Guang-ming，LIU Dan-hua，GAO Da-hua，et al.Research Progress on the Theory of Compressed Sensing［J］.Journal of Electronics，2009，37（ 05）:1070-1081.

［6］ Chenhao Qi，Lenan Wu.A Hybrid Compressing Sensing Algorithm for Sparse Channel Estimation in MIMOOFDM Systems［J］.IEEE Transactions on Signal Processi ng，2011，58（01）:3488-3491.

［7］ 何雪云，宋荣斱，周克琴.基于压缩感知的OFDM系统稀疏信道估计新方法研究［J］.南京邮电大学学报:自然科学版，2010，30（02）:60-65. HE Xue-yun，SONG Rong-zhuo，ZHOU Ke-qin.New Method of Sparse Channel Estimation for OFDM System based on Compressed Sensing［J］.Journal of Nanjing University of Posts and Telecommunications（Natural Science Edition），2010，30（02）:60-65.

［8］ 王妮娜，桂冠，苏冰涛等.基于压缩感知的MIMOOFDM系统稀疏信道估计方法［J］.电子科技大学学报，2013，42（01）:59-62. WANG Ni-na，GUI Guan，SU Bing-tao，et al.Sparse Channel Estimation Method for MIMO-OFDM System based on Compressed Sensing［J］.Journal of Electronic Science and Technology of the University of Electronic Science and Technology of the University，2013，42（01）:59-62.

［9］ CANDES E J.The Restricted Isometry Property and Its Implications for Compressed Sensing［J］.Comptes RendusMathematique，2008，346（09/10）:589-592.

［10］ Donoho D L.For Most Large Underdetermined Systems of Equations，the Minimal l1 Norm Near-solution Approximates the Dparsest Near-solution ［J］.Communications on Pure and Applied Mathematics，2006，59（07）:907-934.

［11］ Chen S，Donoho D L，Sanuders M A.Atomic Decomposition by Basis Pursuit［J］.SIAM Journal on Scientific Computing，2001，43（01）:129-159.

［12］ Sundman D，Chatterjee S，Skoglund M.Greedy Pursuits for Compressed Sensing of Jointly Sparse Signal［C］. In Proc. Eur. Sig. Proc. Conf.，2011.

［13］ Dennis Sundman，Saikat Chatterjee，Mikael Skoglund. Greedy Pursuits for Distributed Compressed Sensing［C］. In Proc. Eur. Sig. Proc. Conf.，2012.

杨 亮（1990—），男，硕士研究生，主要研究方向为认知无线电、宽带频谱通信技术；

齐丽娜（1973—），女，博士研究生，副教授，主要研究方向为认知无线电网络中的频谱资源相关理论、宽带无线通信技术。

Channel Estimation of MIMO-OFDM System based On Compressive Sensing

YANG Liang， QI Li-na
（College of Telecommunication & Information Engineering， Nanjing University of Posts and Telecommunications， Nanjing Jiangsu 210003， China）

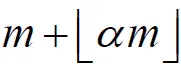
compressive sensing； channel estimation； multi-input and multi-output； orthogonal frequency division multiplexing； extended orthogonal matching pursuit

National Basic Research Program of China （973 Program） （No.2013CB329005）； National Natural Science Foundation of China（No.61471201）

TN911.1

A

1002-0802（2016）-10-1280-07

10.3969/j.issn.1002-0802.2016.10.003

2016-06-08；

2016-09-20

data:2016-06-08；Revised data:2016-09-20

国家重点基础研究发展计划（973计划）基金资助项目（No.2013CB329005）；国家自然科学基金（No.61471201）