基于神经网络的烟丝填充值预测模型研究
2016-11-12陆玉浩王彬彬万云飞王广超牛汝萍冀海波
陆玉浩,王彬彬,万云飞,王广超,牛汝萍,张 娟,杨 莹,冀海波
(1.山东中烟工业有限责任公司滕州卷烟厂,山东 滕州 277500; 2.山东中烟工业有限责任公司技术中心 济南 250013)
基于神经网络的烟丝填充值预测模型研究
陆玉浩1,王彬彬1,万云飞1,王广超1,牛汝萍1,张娟1,杨莹1,冀海波2
(1.山东中烟工业有限责任公司滕州卷烟厂,山东 滕州 277500; 2.山东中烟工业有限责任公司技术中心 济南 250013)
填充值是烟丝的一项重要物理指标。在卷烟制丝生产中,叶组配方和工艺流程一般较为固定,所以制丝工艺参数对烟丝填充值的影响更为直接、突出,但工艺参数对填充值的影响为非线性的,难以根据工艺参数直接推算出烟丝填充值。针对此问题,选取了7个影响较大的工艺参数,采用BP神经网络对7个工艺参数和烟丝填充值间的数量关系进行了初步建模。通过BP神经网络设计和大数据量的训练后,该模型具备了通过工艺参数预测烟丝填充值的能力,预测结果的相对误差为4%左右,这为工艺参数和填充值之间的相互调整提供了理论依据和仿真方法。
BP神经网络;工艺参数;填充值
烟丝填充力是指单位重量的烟丝在一定压力下,经过一定时间后所保持的体积[1]。烟丝填充值不仅影响卷烟的外观与吸食品质,而且是一个反映卷烟生产成本与原料消耗的经济指标,是卷烟加工烟丝的一个重要物理指标[2-3]。影响烟丝填充值的主要因素有物理因素和化学因素,刘建军[4]又将影响因素细分为农艺措施、工艺措施、生物活动、物理特性和化学成分。而在卷烟制丝生产中,影响填充值的主要因素则可以概括为叶组配方、工艺流程和工艺参数。一般来说,在某牌号卷烟的生产过程中,叶组配方和工艺流程较为固定,所以制丝工艺参数对烟丝填充值的影响显得更为直接、突出。然而,工艺参数对填充值的影响为非线性的,难以根据工艺参数直接推算出烟丝填充值。BP神经网络是最为成熟的一种人工神经网络模型,能有效地解决非线性问题,得到了广泛的应用[5]。BP神经网络属于多层前向反馈的有导师学习网络,与普通正向传播神经网络相比,增加了误差反馈环节,通过不断调整所有层的权值,达到减小误差的目的[6-7]。本文将采用BP神经网络对工艺参数和烟丝填充值间的数量关系进行初步建模,并通过BP神经网络设计和大数据量的训练后,使模型具备通过工艺参数预测烟丝填充值的能力,以为工艺参数和填充值之间的相互调整提供理论依据和仿真方法。
1 材料与方法
1.1材料与设备
滕州卷烟厂某牌号完整叶组配方原料。WQ392a滚筒式烟片回潮机、SJ1106a热风加料机、WQ314A型滚筒式叶片增湿增湿机、SH92气流干燥设备。
1.2烟丝取样与填充值测定
待生产正常后,在烟丝干燥工序出口处,用取样盘随机取样100 g,置于样品盒中。样品在空气温度(20±1) ℃、相对湿度(60±5)%条件下平衡24 h。烟丝填充值测定参照烟草行业标准方法(YC/T 152—2001)[8]。
1.3样本数据的确定
根据试验和日常生产数据积累,得到了176组原始数据。为了便于给神经网络提供样本,将其提取成输入样本P和输出样本T,其中输入样本包括松散回潮出口物料含水率、切丝宽度、叶丝增温增湿热风温度、叶丝增温增湿出口物料含水率、叶丝气流干燥燃烧炉温度、叶丝气流干燥混合风温和、叶丝气流干燥出口物料含水率7个对填充值影响较大的工艺参数[9-13],输出样本包括烟丝填充值1个参数。
由于样本中含有不同的物理量,且数值差别很大,样本数据没有可比性,严重影响模型的收敛可靠性及收敛速度,所以在进行训练之前,必须对样本数据进行归一化处理,即将所有数据换算成为[0,1]之内的数。归一化处理如下式所示:
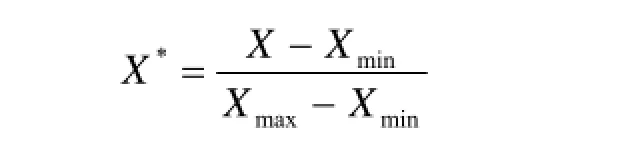
式中:
X——真实值;
Xmax、Xmin——真实值的最大值和最小值;
X*——归一化后的值。
经过数据处理,输入样本均匀地分布在0到1之间,构成了可用的神经网络样本。将数据处理后的原始样本P和T分别分成两组,一组为训练样本p_tr和t_tr,另一组为检验样本p_te和t_te,其中:训练样本为7×150和1×150的矩阵,输入与输出对应,共150个样本;检验样本为7×26和1×26的矩阵,共26个样本。
1.4BP神经网络模型的确定
BP神经网络模型的确定就是对层数、每层的神经元数、初始权值和阈值、训练函数、学习速率等网络参数进行选择。目前,网络参数的选择虽有一些指导原则,但更多的是靠经验和试验。
1.4.1网络层数的确定 为简化网络并降低训练网络权值的时间,根据烟丝填充值预测问题的特点将网络结构定为3层,即网络的隐含层数为1层,结构如图1所示。本研究以7个工艺参数为神经网络的输入层,以烟丝填充值作为神经网络的输出层,即输入层的神经元个数为7个,输出层的神经元个数为1个。
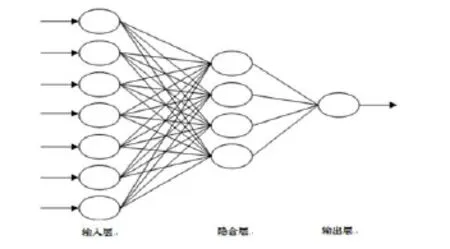
图1 三层BP网络结构Fig.1 Structure of the three layer BP network
1.4.2网络隐含层神经元数的确定 隐含层神经元数是BP网络的一个关键参数,神经元个数过多将导致神经网络归纳能力下降,神经元个数过少将导致神经网络的学习能力不够。隐含层神经元数的一般选择原则是:在能正确反映输入输出关系的基础上尽可能选取较少的神经元数,从而使网络更为简单。目前,隐含层神经元数目的选取尚缺少结论性的方案,诸多选取公式也只是根据经验总结出来的,隐含层神经元数最终的确定仍然需要通过反复测试和结果分析获得。综合诸多因素,本研究使用统计多次循环测试结果的方法进行分析,即采用随机初始化网络,选用固定的训练样本和训练函数,测试并记录隐层节点数分别为3,4,5,6,7,8,9,10,11,12时的训练结果,对参数取平均值,最终分析相关指标综合确定最佳隐层节点数。
1.4.3初始权值和阈值的确定 BP神经网络学习的第一步就是对权值和阈值进行合适的初始化。训练BP网络时,如果对权值和阈值进行的初始化不适宜,可能导致训练时间的增长,特别是当初始权值相等时,可能使误差曲面陷于局部最小。由于系统是非线性的,初始值对学习是否达到局部最小,是否能够收敛以及训练时间长短的影响很大。本研究采取随机赋值方式确定初始权值和阈值,为避免局部极值问题,要选取多组初始权值,最后选用最好的一种。
1.4.4传递函数的选择 BP神经网络存在非线性传递函数使其具有很强的非线性映射能力。传递函数能限制神经网络运行的动态范围,避免输出数据产生大量极端值。在非线性传递函数中,Sigmoid函数用得最为广泛,其与真正的神经元较为相似,且是可微函数,导数较易计算,因此非常适合BP神经元。常用的Sigmoid函数有对数S型传递函数和双曲正切S型传递函数。根据需要,本研究隐含层选择双曲正切S型传递函数,而输出层选择对数S型传递函数。
1.4.5训练函数的选择 训练函数对神经网络的训练精度、收敛速度等产生直接影响,是神经网络性能的重要影响因素。在本研究中,我们通过试验对比选择合适的训练函数。首先设定好隐含层神经元数、最大训练次数、网络目标误差精度、学习速率等参数,然后再采用不同的训练函数对相同的训练样本进行训练,最后对比训练过程。通过分析各种训练函数的训练过程发现,trainlbr函数在所有的训练函数中收敛速度最快(即达到极小值的速度是最快),而且训练步数也最少,所以本研究选择trainbr函数作为神经网络的训练函数。
1.4.6学习速率的选择 在BP神经网络学习时,我们需要选择合适的学习速率来控制网络学习过程中网络权值变化幅值的大小,学习速率太小则会使得收敛变慢,学习时间变长;学习速率太大,网络达到全局最小的可能性将增大,但可能会出现网络来回振荡和过度收敛现象。学习速率一般在0.01~0.7之间选取。对于学习速率选择只能进行试选,然后根据训练情况选择一个合适的学习速率反复训练。结合实际要求,通过仿真试验讨论,初选学习速率为0.01。
通过神经网络的隐层节点数、传递函数、训练函数和学习速率等结构参数的仿真试验,最终确定神经网络的结构参数如表1所示。
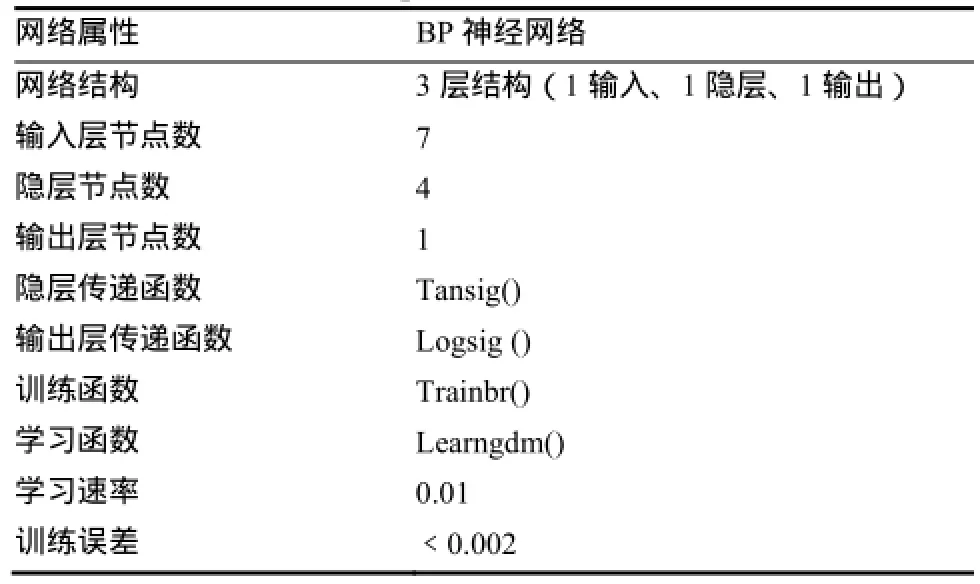
表1 神经网络结构参数Table1 Structural parameters of the neural network
1.5程序设计及学习
根据上文所建神经网络模型,设定学习速率为0.01,误差e<0.02,训练最大次数10000次,利用Matlab软件编制BP神经网络程序[14-15],主要程序如下∶
Net=newff(minmax(pt),[7,4],{'tansig','logsig'},'trainbr');
net.trainparam.epochs=10000;
net.trainparam.goal=0.002;
LP.lr=0.01;
net=train(net,pt,tt);
y=sim(net,pte);
error=y-tte;
sum=norm(error);
BP神经网络程序按照算法对训练样本进行学习,不断修正权值,直至程序达到了误差要求或虽未达到误差要求但达到了最大学习次数。当学习完成后,神经网络就具有了通过7个工艺参数预测烟丝填充值的能力。随后,可以利用检验样本对神经网络预测模型进行检验,并进一步将模型应用到实际生产中。
2 结 果
2.1样本检验结果
当BP神经网络训练完毕后,利用26个检验样本进行检验,并将得到的神经网络输出值与检验样本值进行比较。由于神经网络的输出值和检验样本值均在0到1之间,不利于观察比较,所以均需进行反归一化,得到烟丝填充值,再将两者进行对比,如图2所示。
由图2可知,样本值折线和预测值折线基本吻合,两者的最大相对误差3.6%,最小相对误差1.41%。对样本值和预测值两组数据进行配对T检验,平均差95%置信区间(-0.0472,0.0449),区间包含0;平均差=0(与≠0)的T检验p值为0.959,无法拒绝原假设,即平均差=0,说明两组数据无显著差异。
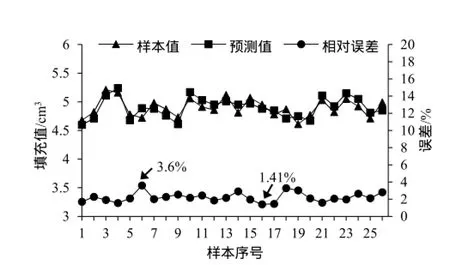
图2 检验结果统计分析图Fig. 2 Statistical analysis of tested results
2.2模型应用预测结果
当BP神经网络检验完毕后,应用该预测模型对正常生产的10批次烟丝进行填充值预测,并与实际检测值进行比较。同样,需先对神经网络的输出值进行反归一化,得到烟丝填充值,再与检测值进行对比,如图3所示。
由图3可知,预测值与检测值吻合度较高,两者的最大相对误差3.12%,最小相对误差1.22%,相对误差较检验时有下降趋势。对检测值和预测值两组数据进行配对T检验,平均差95% 置信区间(-0.0933,0.0833),区间包含0;平均差= 0 (与≠0)的T检验p值为0.901,无法拒绝原假设,即平均差=0,说明两组数据无显著差异。
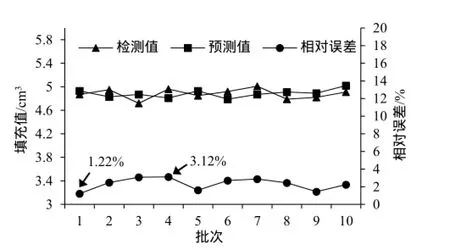
图3 预测结果统计分析Fig. 3 Statistical analysis of predicted results
3 讨 论
由填充值预测模型的检验和运用结果分析可知,预测值和实际值的相对误差小于4%,相对误差在合理范围内,且有下降趋势,结果较理想,这说明预测模型的预测能力较好,已具备了一定的实用性。研究表明[16-18],随着样本的不断丰富,神经网络模型还能通过样本进行再学习,从而产生新的权值分布和阈值,不断提高预测能力。因此,随着烟丝填充值预测模型的不断应用,预测值和实际值的相对误差有进一步减小的可能性。
本研究中选取了气流烘丝线对烟丝填充值影响最大的7个工艺参数(松散回潮出口物料含水率、切丝宽度、叶丝增温增湿热风温度、叶丝增温增湿出口物料含水率、叶丝气流干燥燃烧炉温度、叶丝气流干燥混合风温、叶丝气流干燥出口物料含水率)作为神经网络的输入。在实际运用中,可根据需求适当减少工艺参数个数,以简化神经网络结构;在条件允许的情况下,也可以引入更多的工艺参数作为神经网络的输入,从而达到提高模型预测能力的目的。本文虽然只针对气流烘丝线建立了烟丝填充值预测模型,但滚筒烘丝线预测模型的原理和方法是一致的,只需将神经网络输入层替换为滚筒烘丝筒壁温度、热风温度、滚筒转速等工艺参数。
4 结 论
本研究选取了7个对烟丝填充值影响较大的工艺参数,采用BP神经网络对工艺参数和烟丝填充值间的数量关系进行了初步建模,并经过MATLAB编程和训练后使该模型具备了通过工艺参数预测烟丝填充值的能力,预测结果的相对误差为4%左右,预测能力较好,为工艺参数和填充值之间的相互调整提供了理论依据和仿真方法。
[1] 荆聪莹,杜咏梅,侯小东,等. 烤烟填充值与主要理化指标的关系研究[J]. 中国农学通报,2013,29(30):202-205.
[2] 于建军. 卷烟工艺学[M]. 北京:中国农业出版社,2009.
[3] 刘新民,杜咏梅,程森,等. 烤烟烟丝填充值与其理化指标和感官品质的关系[J]. 中国烟草科学,2012,33(5):74-78.
[4] 刘建军. 烟叶填充值的研究进展[J]. 安徽农业科学,2015,43(1):244-245,297.
[5] 梁瑞海,崔源. 使用神经网络预测膨胀烟丝的填充值[J]. 烟草科技,2008(4):9-10.
[6] 王彦闯. 农产品检测电子鼻的模式识别算法和软件编程的实现[D]. 杭州:杭州电子科技大学,2010.
[7] 李丽霞,王彤,范逢曦. BP神经网络设计探讨[J]. 现代预防医学,2005,32(2):128-130.
[8] 国家烟草专卖局. YC/T152—2001卷烟烟丝填充值的测定[S]. 北京:标准出版社,2001
[9] 魏玉玲,阴耕云,李绍臣,等. 几个重要制丝工序对烤烟烟丝填充值和碎丝率的影[J]. 云南大学学报:自然科学版,2010,32(S1):183-186.
[10] 李艳,杨雷. 运用六西格玛方法提高叶丝填充值[J]. 工业工程与管理,2010,15(6):131-136.
[11] 刘国栋,王旭锋,李向阳. 制丝工艺参数对烟叶叶丝耐加工性和填充值的影响[J]. 河南农业科学,2015,44(8):145-148.
[12] 姚光明,乔学义,申玉军,等. 烤烟叶片在不同叶丝干燥工序中叶丝填充值和整丝率的变化[J]. 河南农业科学,2011,40(2):9-73.
[13] 杨美丽. 不同工艺参数对烟丝质量影响的研究[J]. 科学之友,2012(4):144-145.
[14] 涂春霞,刘小俊. VB与HATLAB混合编程原理概述[J]. 可编程控制器与工厂自动化,2008(7):32-35.
[15] 李善姬,芦成刚. 采用VB与MATLAB混合编程的数字滤波器设计[J]. 计算机工程与设计,2006,27(18):3487-3490.
[16] 周泽弘,曹淋海,王昌全,等. 基于RBF神经网络建立库存烟叶香型的预测模型[J]. 中国烟草科学,2016,37(2):65-70.
[17] YIN Yan, BAO Jiusheng, YANG Lei. Tribological properties prediction of brake lining for automobiles based on BP neural network[C]//Proceeding of the 22nd Chinese Control and Decision Conference (2010 CCDC), Xuzhou,China∶ IEEE, 2010∶ 2678-2682.
[18] 肖协忠,王放,贺英,等. 烤烟致香成分与香气质量的相关性分析[J]. 中国烟草科学,2008,29(6):1-6.
Study on the Forecasting Model of Cut Tobacco Filling Value Based on the Neural Network
LU Yuhao1, WANG Binbin1, WAN Yunfei1, WANG Guangchao, NIU Ruping1,ZHANG Juan1, YANG Ying1, JI Haibo2
(1. Tengzhou Cigarette Factories of Shandong Tobacco Industrial Co., Ltd., Tengzhou, Shandong 277500, China; 2. Technology Center of Shandong Tobacoo Industrial Co., Ltd., Jinan 250013, China)
The filling property is a vitally important physical index of cut tobacco. Due to the similar cigarette blending formulation and fixed technological process in cigarette production, relevant technological parameters have direct and significant influence on the filling value of cut tobacco. However, the relationship between the parameters and filling value is nonlinear, which makes it difficult to calculate filling values of cut tobacco directly based on the parameters. Therefore, seven most important technological parameters were selected, and the quantitative relation model between various parameters and the filling value was established with the BP neural network. Further, the model was designed with the BP neural network and trained through a large amount of data, so it could forecast the filling value according to the seven technological parameters and the relative error of forecasting results was about 4%. The establishment of the forecasting model provides a theoretical basis and simulation method for the mutual adjustment between the technological parameters and the filling value of cut tobacco.
BP neural network; technological parameter; filling value
TS41+1
1007-5119(2016)05-0082-05
10.13496/j.issn.1007-5119.2016.05.015
陆玉浩(1989-),男,硕士,主要从事烟草工艺研究。E-mail:luyuhao19890629@163.com
2016-03-10
2016-07-04
