我国地区高等教育发展水平的综合评价

李倩男 姚宁宁

（中国地质大学（武汉），湖北武汉430074）

我国地区高等教育发展水平的综合评价

李倩男 姚宁宁

（中国地质大学（武汉），湖北武汉430074）

文章利用因子分析方法，计算我国31个地区（除香港、澳门、台湾）2008-2013年每一年的高等教育发展水平的因子得分；然后利用熵权法计算每年因子得分的熵权，根据得到的熵权，计算这6年的综合评价值并进行排序。这样可以从整体上对我国近几年的高等教育发展状况进行了解，为更好地指导和规划高等教育事业的健康发展提供一定的科学依据。

因子分析；熵权法；高等教育

一、概述

受到社会对高等教育强烈需求的影响和高等教育改革潮流的有力驱动，21世纪高等教育的普及性、多样化性、终生教育等基本特征已日益清晰地展现在人们面前。近几年高等教育实施扩招政策，我国对高等教育非常重视。

对高等教育发展的评价是对高等教育发展现状的认识，只有认识高等教育发展的状况和特性才可以制定良好的政策来促进高等教育更好的发展。对高等教育发展水平的综合评价有很多种方法，如：层次分析法、主成分分析法、因子分析法、熵权法等，但都是对某一年份的高等教育发展水平的综合评价。我国已经进入高等教育大众化，但是我国高等教育大众化还在探索中［1-3］。仅对一年的高等教育发展情况进行评价不足以反映近几年高等教育发展的本质。为了解近几年我国高等教育的发展状况，需要对每年的高等教育发展水平的综合评价进行比较分析、整体分析。

文章利用SPSS软件对2008-2013年每一年的高等教育发展进行因子分析，计算综合得分并排序［4］，然后把每年的综合得分运用熵权法结合起来，利用MATLAB软件计算每年的熵权和总得分，并进行排序，来反映2008-2013年这几年高等教育的总体发展状况。

二、指标选取及因子分析

（一）数据的来源和指标的选取

原始数据是取自2009-2014年的《中国统计年鉴》、《中国教育统计年鉴》和《中国教育经费统计年鉴》。

根据指标的选取原则，选取比较全面和切实可行的21个指标，反映高等教育规模的指标：在校大学生数、在校研究生数、普通高校数、211院校数、每十万人口平均在校生数；反映教育结果的指标：毕业生数、毕业生中研究生比例；反映高等教育的人力投入指标：普通高校师生比、教职工数、专任教师数、副高级以上专任教师比、博士学位专任教师比；反映高等教育的物质投入指标：人均占地面积、人均图书、人均计算机数、人均固定资产值；反映高等教育的财力投入指标：高等教育经费总收入、国家财政性教育经费、国家财政性教育经费占地区GDP的比例、生均教育经费支出、生均财政预算教育经费支出。

（二）用因子分析进行综合评价

因子分析的基本思想是根据相关性的大小把原始变量分组，使得同组内的变量之间相关性较高，不同组的变量相关性较低。

运用SPSS软件对2008-2013年的数据进行因子分析［5-7］，进行因子分析之前需要先对数据进行相关性检验。2008-2013年相关性检验的KMO值分别是：0.709、0.755、0.796、0.731、0.786、0.749，KMO的值都在0.7到0.8之间，巴特莱特球度检验的sig值都显著为0，选取的指标都通过了KMO检验和巴特莱特球度检验，表明数据间具有一定的相关性，2008-2013年每年都可用这些指标进行因子分析。

1.征值及累计累积贡献率

每年的因子分析都采用主成分法和最大方差旋转法，得到因子的特征值和贡献率及旋转后的特征值及贡献率。通过比较可知，即使相同的指标，不同的年份进行因子分析，特征值不同，累积贡献率也不同。每年特征值大于1的个数都是3个，累积贡献率都大于85％。2008-2013年的累积贡献率分别为：85.873％、87.161％、86.878％、87.716％、88.29％和88.15％。

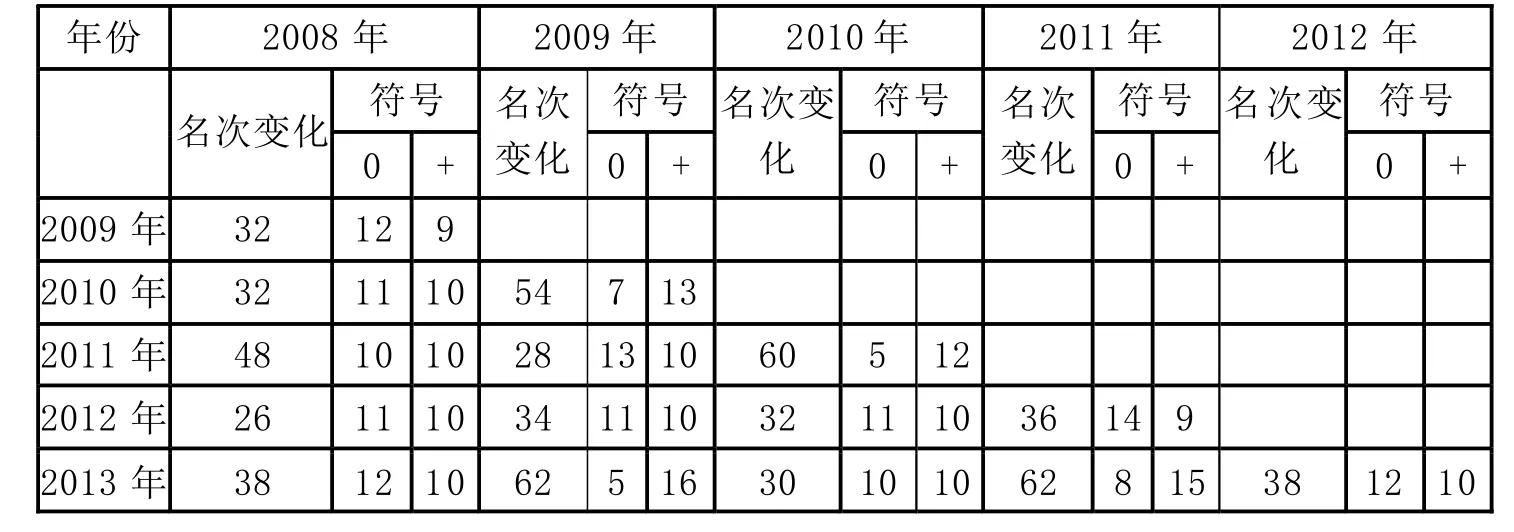
表1　年份间相比排名变化及排名符号变化的情况

2.因子载荷分析

对各年进行因子分析，提取特征值大于1的因子。2008-2013年每年都提取3个因子，但是因子的较高载荷的指标有差别。2008年较高载荷指标与其他年份都不同，2009年、2011年和2012年选取的3因子在相同的指标上有较高的载荷，2010年和2013年选取的3因子在相同的指标上有较高的载荷。每个因子都对应实际的意义，但不同年份因子的高载荷不同，每年的因子含义也不相同。

3.综合评价

每年选取的指标相同，计算每年的因子得分，每年的因子得分之间具有很强的相关性。每年的因子得分的标准差也相差不大，但是排序有变化。每年的综合排序不同，连续年份排序差异也很大，用名次差的绝对值和作为年份间排名相比较的名次变化情况（表1）。

通过表1可以看出每年的名次都有变化，变化最大的名次差的绝对值和是62；变化最小的名次差的绝对值和是26。再比较排名的符号变化情况，其中“0”表示名次没有变化，“+”表示名次落后，排名进步的次数就等于没有变化的次数减去名次落后的次数。每年的排名相比较都有变化。排名没有变化的个数最多的是14个，其次是13个，排名没有变化的最少个数是5个，可知近几年大部分省份的名次都发生了变化。各省份进步的个数与落后的个数相比，相差较大的是6、7；相差最小的是0，其余的是1、2，说明除了两个特别，其余排名的进步个数和落后个数相比变化不大。

通过上述比较可知，每年的排名都有变化，而且变化量也不少，所以仅以一年的高等教育数据来评判高等教育发展水平不是很全面，需要选取多年高等教育数据来评判高等教育的发展状况。

2008-2013年这6年排名变化最大的是青海，变化10名；其次是甘肃，变化9名；再次是新疆，名次变化7名；一直不变的是北京、上海、江苏；变化1名的有天津、吉林、湖北、重庆和四川，变化2名的有辽宁、浙江、安徽、江西、湖南、广西、云南和陕西。说明短短的6年，我国31个省市的高等教育发展水平的综合情况有很大变化。

每年的高等教育发展水平都有所变化，一年的高等教育发展水平的综合评价只能说明当年高等教育的发展状况，要想了解一段时间内高等教育的发展水平，就需要考虑连续几年的高等教育发展水平的变化情况。仅对一年的高等教育发展水平进行综合评价不足以反映近几年的高等教育发展水平，仅比较每年的综合排序也是不充分的，有必要引入反映近几年高等教育发展水平的综合方法，对近几年的高等教育发展水平进行综合分析来反映高等教育发展的实质。我们运用熵权法对2008-2013年的高等教育发展水平进行客观的综合评价。

三、运用熵权法进行综合评价

（一）熵权法基本理论

熵权法是一种在综合考虑各因素指标提供信息量的基础上计算综合指标的方法。作为客观综合定权法，其主要根据各指标传递的信息量的大小来确定权重。熵权法的基本思路是根据指标变异性的大小来确定客观权重。一般来说，若某个指标的信息熵越小，表明指标值的变异程度越大，提供的信息越多，在综合评价中所起到的作用也越大，其权重也越大。相反，某个指标的信息熵越大，表明指标值的变异系数越小，提供的信息也越小，在综合评价中所起到的作用也越小，其权重也就越小［8］。

（二）实证分析

为了求得2008-2013年间我国高等教育的整体发展水平，选择每年的因子总得分作为指标。利用熵权法计算每年的权重，每年权重的大小表示对因子得分的贡献大小。

1.综合评价

以我国31个省份作为评价对象，运用MATLAB软件计算熵权，得到2008-2013年每年的信息熵依次是0.9252、0.9337、0.9035、0.9292、0.9098、0.9105；2008-2013年每年的熵权依次是0.15329、0.13592、0.19758、0.14502、0.18488、0.18331。

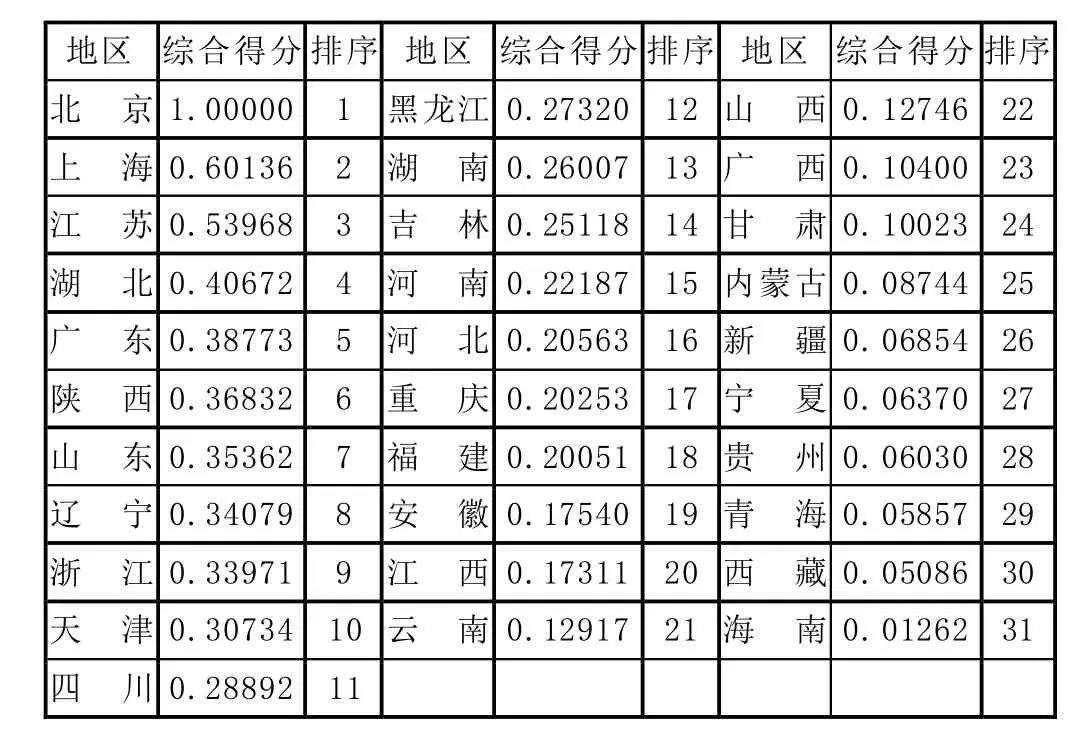
表2　熵权法综合得分及排名

2010年的因子得分信息熵最小，表明2010年的因子得分的变异程度最大，提供的信息最多，权重值最大，权重值是0.19758；而2009年因子得分信息熵最大，表明2009年因子得分变异系数最小，提供的信息最少，权重值最小，权重值是0.13592。利用熵权法计算2008-2013年的高等教育发展水平的综合评价值及排序（表2）：

由熵权法得到的综合得分与2008-2013年的因子得分相关性很强，因子得分和总得分都是反映高等教育发展水平。从表2可以看出，前三名分别是北京、上海和江苏。北京市、上海市、江苏省在每年的因子得分上都是前三名。后三名分别是青海、西藏和海南，海南省有四年是最后一名，另外两年分别第28名和29名，西藏有两年30名，另几年的名次分别是26、28、29、31名，青海有两年是28名，另几年的名次分别是21、23、30、31名，后几年的排名变化有些大。除了前三名，其他省份的名次在这6年期间都有所变化。

2.总排名与每年排名的比较

总排名与每年的因子排序相比较，也用名次差的绝对值和作为名次变化大小（表3）。总排名与2011年的名次的变化量最大，达到42；总排名与2012年的名次变化量的最小，变化量为10。与表1相比较可知，比26小的有三个，表2中的最大值42小于62，说明利用熵权法得到的综合评价很可靠，综合了每年的高等教育发展水平，反映了这六年的高等教育发展水平的整体情况。

再比较排名的符号变化情况，其中“0”表示名次没有变化，“+”表示名次落后，“-”表示名次进步，总排名与每年排名相比较都有变化。排名相比较没有变化的个数最多的是2012年的22个，最少的是11个，其它年份排名没有变化个数近一半。排名前进的个数和排名落后的个数相差最大的个数是2，与年份之间的排名相比，排名变化不大。说明综合评价充分利用了每年的因子得分，反映了近几年的综合情况。

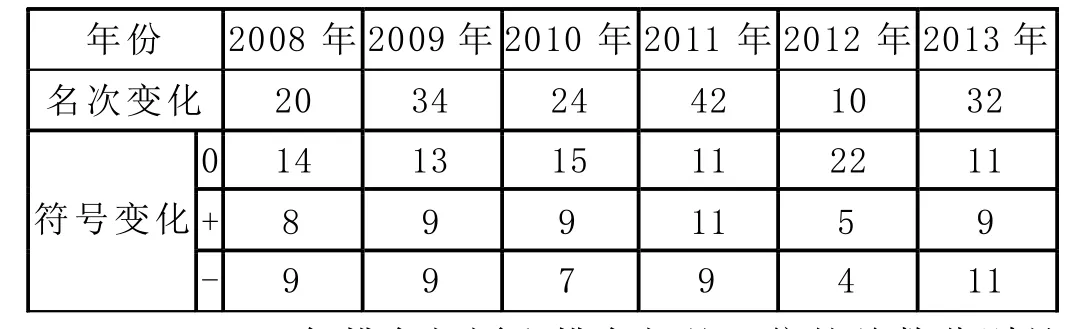
表3　总排名与各年排名的名次差的绝对值和和符号变化情况

2008-2013年排名相同和排名相差一位的总数分别是29、23、25、21、30、24，相差两名及更少的总数分别是30、26、29、27、31、28，说明大部分省市各年排名与总排名名次的变化不大。排名相差最大的是2011年青海省与总排名相差8名，2009年的青海和2011年甘肃与总排名相差6名。说明了利用熵权法得到的排名充分结合了各年的高等教育发展信息，每年的因子得分是当年高等教育发展水平的表现形式，充分利用每年因子得分就表示充分利用了每年的高等教育发展的信息，也说明了熵权法排名的合理性，整体的排名是2008-2013年这6年31个省市高等教育发展水平的整体反映。

我国东中西部划分为：东部地区：辽宁、河北、北京、天津、山东、江苏、上海、福建、台湾、广东、香港、澳门、海南；中部地区：黑龙江、吉林、山西、河南、安徽、湖北、湖南、江西；西部地区：内蒙古、甘肃、陕西、宁夏、四川、贵州、重庆、广西、新疆、青海、西藏。

通过比较发现，西部地区关于高等教育发展的分类，大部分排名再最后，西部地区不仅是我国经济欠发达地区也是我国高等教育欠发达地区。东部地区的排名比较分散，东部地区是我国经济发展最快的地区，但不足的地方是人均面积没有西部的大；大部分高职称和高学历老师都愿意去东部发展，研究生在东部和西部的比例也相差较大；在教育经费方面，西部地区的总经费投入也很少，人均图书、人均计算机和人均固定资产也是东部大于西部；所以想要高等教育快速发展，不仅在教育物质资源上加大投入，教师资源也必不可少。

通过高等教育发展水平的排名与东中西的划分相比较，可知经济发达的地区高等教育发展不一定好，经济不发达的地区高等教育发展不一定差，这也说明了我国高等教育与经济发展不协调。高等教育只有适应经济的发展需要，才能促进经济的增长，否则，就会阻碍经济的增长，高等教育的发展也离不开经济的支持。改善高等教育的发展方式，使我国高等教育与经济协调健康的发展。

四、结束语

通过因子分析来反映每一年高等教育的发展水平，运用熵权法来反映近几年高等教育的整体发展水平。利用熵权法得到的综合评价充分利用了每年的因子得分，也就是充分利用了每年高等教育发展信息。综合高等教育发展信息来对高等教育发展水平进行综合评价，削弱了随机因素的影响，使得综合评价更可靠准确。

综合评价是为了表示近几年高等教育的发展水平的差异，排名表示每个省市发展的不一致的比较，分类表示地区间高等教育发展的差异情况。通过排名和分类可知，经济发达的地区，高等教育发展不一定好，经济不发达的地区，高等教育发展不一定差。我国西部地区高等教育发展水平比东部地区落后很多，为了我国高等教育全面协调的发展，要加快西部地区高等教育发展的步伐。高等教育只有适应经济的发展条件才可以促进经济的发展。要对高等教育发展落后于经济发展的地区给予重视，制定合理的政策使高等教育适应经济的发展。

［1］李建宁.我国区域高等教育发展水平的统计分析［J］.山西财经大学学报，2007，10（4）.

［2］王素，方勇，孙硫泽.高等教育竞争力：模型、指标与国际比较［J］.教育研宄，2012，34（7）：122-129.

［3］张秀萍.我国省域高等教育竞争力研究［D］.辽宁:大连理工大学，2013.

［4］李卫东.应用多元统计分析［M］.北京：北京大学出版社，2008.

［5］王昱，熊科.东部地区高等教育发展水平的因子分析［J］.高教探索，2013（6）：53-56.

［6］朱永东，向兴华，叶玉嘉.基于因子分析的美国高等教育发展水平综合评价研究［J］.高教探索，2014（5）：68-73.

［7］朱茂勇.基于因子分析的高等教育发展水平差异的实证研究［J］.中国高等教育评估，2015（1）：31-36.

［8］王金湘.基于熵权法的企业自主创新能力评价——以浙江省为例［J］.经营与管理，2014（1）：103-105.

This paper uses the factor analysis method to calculate factor score of the development level of higher education of 31 areas in China（with the exception of Hong Kong，Macao and Taiwan）every year in 2008-2013，then uses entropy method to calculate the entropy weight of factor score of every year，and according to the entropy weight，calculates comprehensive evaluation of the six years，sorting.We can understand the situation of the development of higher education on the whole in recent years in our country，and provide certain scientific basis to better guide and plan the healthy development of higher education.

factor analysis；entropy method；higher education

G640

A

2096-000X（2016）22-0256-03