反时限过流保护整定优化研究
2016-11-11田君杨
黄 超, 杨 彦, 田君杨
(广西电网电力调度控制中心,广西南宁530023)
反时限过流保护整定优化研究
黄超, 杨彦, 田君杨
(广西电网电力调度控制中心,广西南宁530023)
反时限过流保护因动作曲线配合困难掩盖了其在原理上紧密反映短路电流变化的固有优势,一定程度限制了其应用。为此,在深入分析保护动作曲线之间严格配合的基础上,从保护选择性角度提出了反时限过流保护之间、反时限保护与定时限保护、定时限保护与反时限保护的整定配合原则;并在保证灵敏性的前提下,采用压缩因子粒子群优化算法(K-PSO)、辅之曲线参数与选择性配合作为约束条件,从快速性角度建立了整定范围内的时间优化目标。整定原则与优化模型可分别用于反时限过流保护整定计算与定值优化,有助于提高国内反时限过流保护的工程实用价值。算例分析验证了该方法的有效性与可行性。
反时限过流保护;保护配合;选择性;定值优化;粒子群算法
0 引言
现代电网飞速发展与高度复杂,传统定时限过流保护由于受运行方式等因素影响,其整定配合难度急剧增加,容易造成失配以致保护越级动作,难以满足电网安全稳定运行需求。而在原理上具备紧密反映短路电流变化特征优势的反时限过流保护,与很多负载的故障特性相近,选择性与速动性易同时满足。国外电力系统普遍将其作为输电网后备保护及配网主保护[1],在我国电网的应用则处于逐步增加的状态[2]。
相较于阶跃式定时限保护,具有一定弧度的反时限保护动作曲线存在整定配合困难等缺点[3],极大限制了其应用。因此,目前国内反时限保护多用于配合关系较少的单元件保护(如发电机[4]、电动机等)、微网保护[5-6]、配网保护[7-8]及微机保护反时限算法研究[9];涉及元件之间配合,则文献研究甚少[10-12],工程中则常采取简化方法,比如忽略彼此配合,统一取固定值,既严重削弱了反时限保护的优势,亦存在不严格配合带来的隐患与风险。
鉴于此,本文以反时限过流保护选择性与快速性为核心,建立了反时限过流保护之间配合、反时限与定时限保护配合的整定原则,并定义了整定范围内的时间优化目标,将优化算法融入整定计算软件,得到满足工程需要的保护定值。
1 反时限过流保护曲线特性
保护动作时间随故障电流的增加而减小是反时限过流保护的基本特征,学术界、工程界通常将反时限动作时间-故障电流特性曲线拟合,得到其通用动作方程:
(1)
式中:TDS(Time Dial Setting, TDS)为时间系数(0.05~1.1);t为保护动作时限;Ik为流过保护处的短路电流;Iop(Pickup Current Setting)为动作电流,整定时要求满足下式:
(2)
式中:IL.max和Ik.min分别为最大负荷电流和最小短路电流。K1~3为曲线常数,本文以电网常采用的一般反时限曲线(K1=0.14,K2=0.02,K3=-1)且线路元件配合为例进行研究。
2 反时限过流保护选择性分析
线路反时限过流保护选择性体现为本元件后备保护时间比相邻元件保护时间留有足够裕度,即在保护范围内电流-时间动作曲线上两曲线没有交集。以图1所示系统为例,保护R1与R2配合特性曲线如图2所示[13],动作时间分别为t1与t2,见式(1)。选择性满足要求,即要求在保护范围内下式成立[14]:
(3)

图2 保护配合特性曲线

图1拓扑图
下面分别分析线路反时限过流保护之间配合及与定时限保护之间配合情况。
2.1线路反时限过流保护之间配合
图1所示系统中保护R1与R2均为一般反时限,其配合特性曲线如图2所示。R1曲线方程可通过点E、B两点确定,见图2(a)。点E确定启动电流Iop1,点B则意味着图1中母线B故障时t1-t2≥ΔT,时间级差ΔT常取0.3 s。而对于母线C故障时,t1与t2大小关系则存在图2(a)、(b)两种情况。若为后者,则意味着线路BC发生故障时,保护R1有可能误动作。
将t1与t2用式(1)表征后代入式(3),则满足式(3)等价于满足:
y=kx-b>0
(4)
式中:
b=TDS1-TDS2
式中:Ik为线路BC故障流过保护R2的电流;Kfz保护R1对R2的分支系数。
式(4)为一元一次函数,当斜率k<0时,理论上存在故障电流数值很大的情况下,y<0,较难满足选择性要求,因此令k>0易于定值整定。
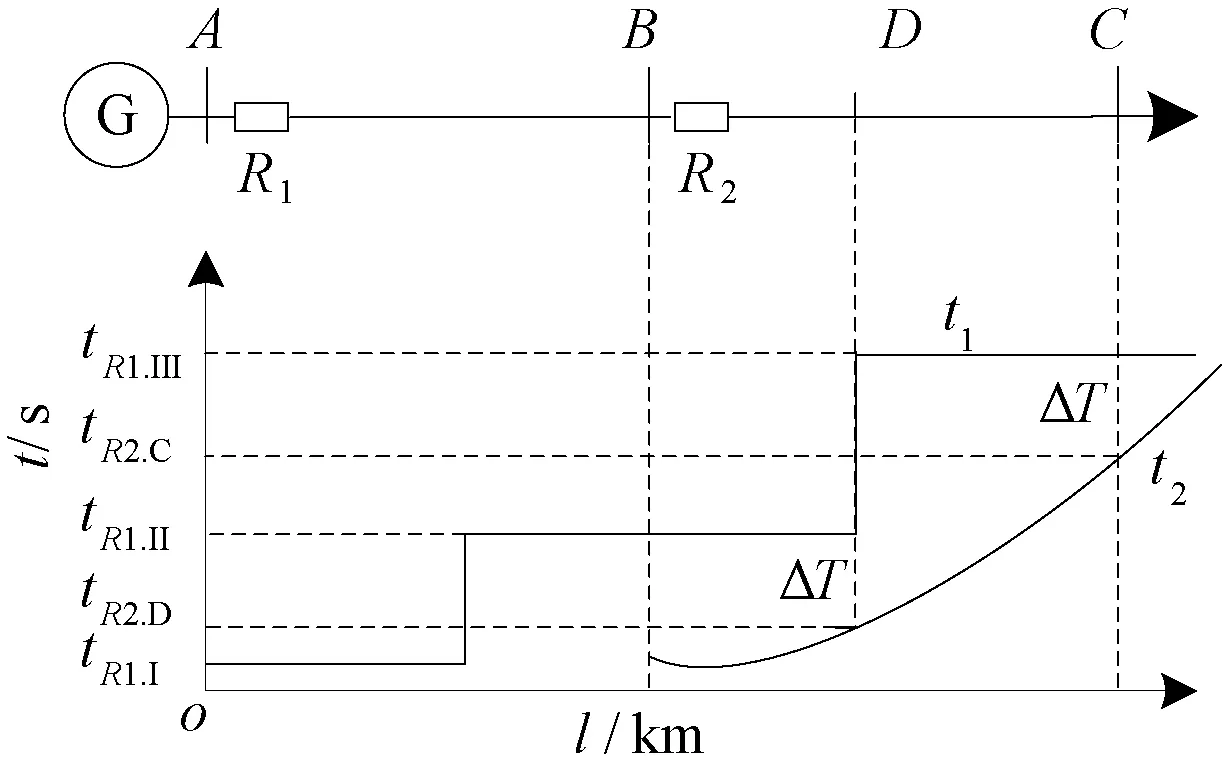
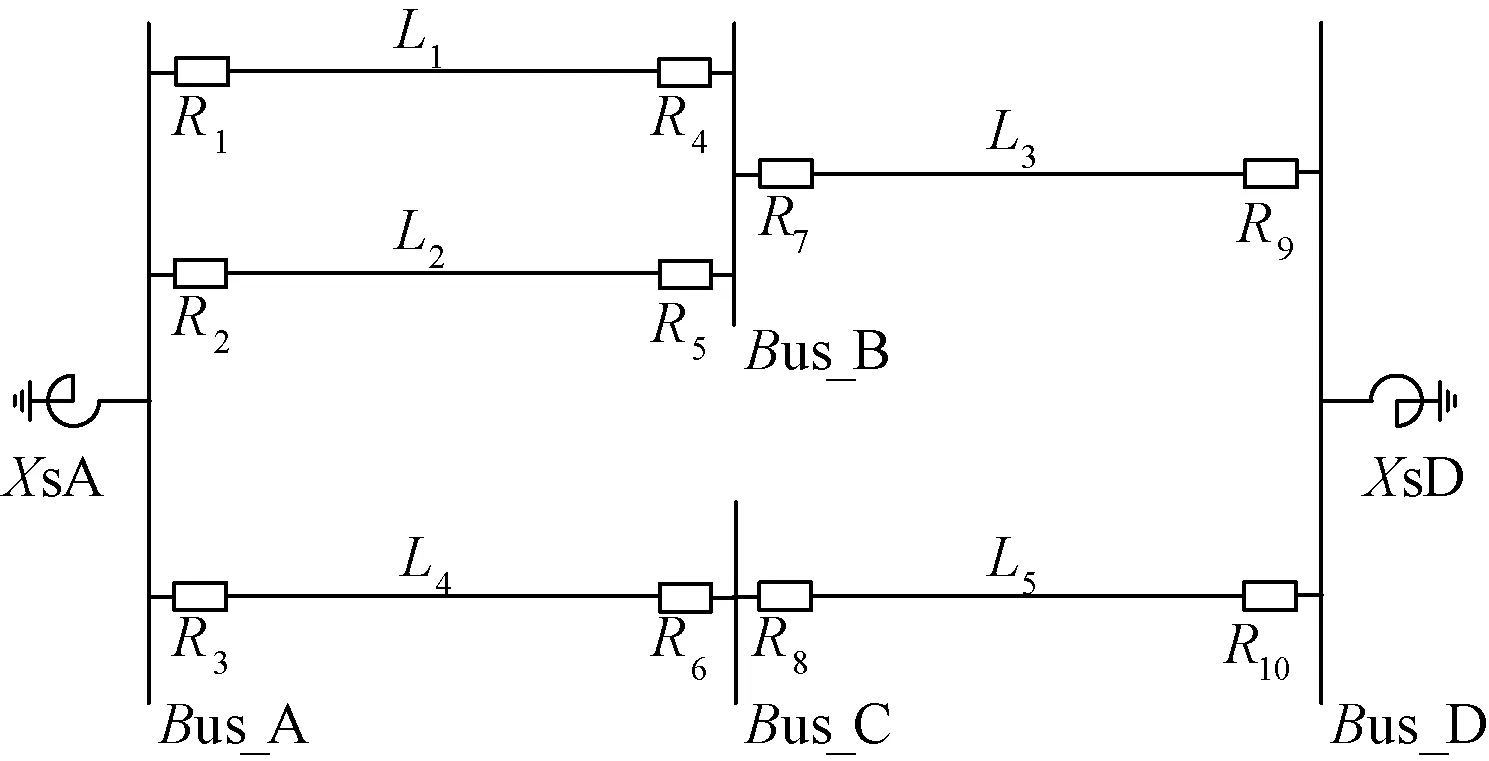
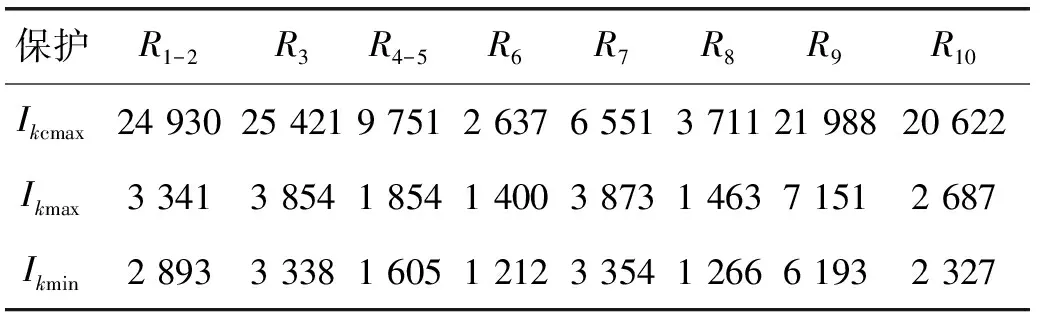
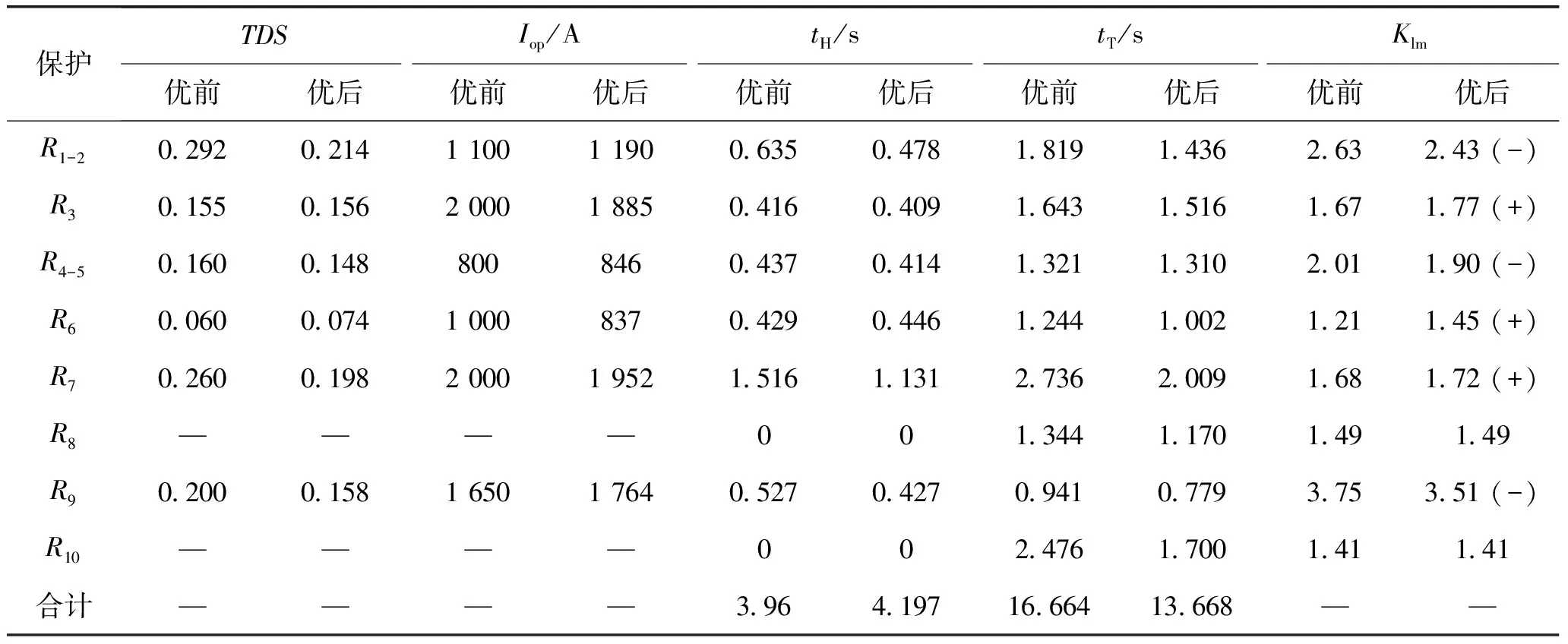
若记Iop_max=max{Iop1/Kfz,Iop2},则只需在Iop_max点满足式(4),加上k>0则保证了线路BC任一点故障均满足了选择性。将Iop1/Kfz>Iop2与Iop1/Kfz 考虑必须保证R2出口(近似B处)故障时满足ΔtB≥ΔT。 因此,保护R1与R2配合满足选择性,即达到图2(a)所示,必须满足下式: (5) 实际整定过程中,Kfz取为最大分支系数。 2.2线路反时限过流保护与定时限保护配合 如图3,保护R1为反时限过流保护,R2为定时限过流保护或距离保护(R2整定原则依照现有规程,本文略);由于R2Ⅱ段保护范围已经伸出该线,故本文仅分析R1与R2两段配合时情况。D处为R2Ⅰ段定值对应的保护范围末端,记在B,D处R1动作时间t1分别为tR1,B、tR1,D,R2的Ⅰ段、Ⅱ段动作时间分别为tR2,I(≈0 s)和tR2.II。保护R1与R2配合满足选择性,必须满足下式: (6) 整定过程中,难点在于确定D位置,若R2为距离保护,则D位置较为固定,距离B约占全线70%~80%;若R2为定时限过流保护,大方式下D处偏离B,小方式下D处偏向B。考虑到传统整定软件在配合时简单将故障点设置在母线C处的做法,建议参照部分整定软件已扩展了提供线路中点(记为M处)故障计算结果的做法。 图3 反时限保护与定时限保护配合 实际应用中,可参照如下步骤在整定软件中完成整定原则代码: (1) 若线路BC配有全线速动保护(如差动保护、纵联保护或其他带极短延时全线保护),时间为tR2.ZL,则整定只需满足式(7)即可,否则执行(2)。 (7) (2) 若由于线路BC太短或大小方式差异太大导致R2Ⅰ段无足够保护范围而退出,则只需满足式(8),否则执行(3)。 (8) (3) 鉴于式(8)为式(6)的一种特例,故直接用式(8)进行计算。若不满足配合或配合困难,则执行(4)。 (4) 用式(6)进行计算,若R2为距离保护,则D取M处进行计算;若R2为定时限过流保护,大小方式均参与,若R2Ⅰ段D处偏向C,则D取M处;若偏向B,则D取B处参与计算。 2.3线路定时限保护与反时限过流保护配合 如图4,R1为定时限保护,R2为反时限保护,动作时间分别为t1和t2。R1在Ⅱ段保护范围末端D处时间为tR1.II,R2该处时间为tR2.D。对于R1远后备Ⅲ段仅考虑C处配合已足够,时间分别为tR1.III、tR2.C。 由图可知,保护R1与R2配合满足选择性必须满足下式: (9) 与上节类似,难点在于确定D位置,若R1为距离保护,则D位置较为固定,距离B约占AB线120%~130%;若R1为定时限过流保护,建议Ⅱ段电流定值按保本线末端(B处)故障有灵敏度整定,Ⅲ段定值按躲最大负荷电流整定。 图4 定时限保护与反时限保护配合 在实际应用中,可参照如下步骤在整定软件中完成整定原则代码实现: (1) 若由于线路BC太短或大小方式差异太大导致R1Ⅱ段伸出C处,则只需满足式(10),否则执行(2)。 (10) (2) 鉴于式(10)为式(9)的一种更苛刻情形,故直接用式(10)进行计算。若不满足配合或配合困难,则执行(3)。 (3) 用式(9)进行计算,若R1为距离保护,则D取线路BC中点M处进行计算;若R2为定时限过流保护,大小方式均参与,若由R1Ⅱ段D处偏向B,则D取M处;若偏向C,则取式(10)参与计算。 (4) 若简化处理,可将tR1.III固定取为比tR1.II增加一个延时。 对于其他元件间保护配合(如变压器反时限过流保护与出线距离或定时限保护配合),均可参照本节所述原则进行整定。 3.1快速性及优化目标 选择性配合原则融入整定软件进行整定计算虽然提高了实践可操作性,但与传统整定配合一样具有仅考虑相邻一或二级的不足,计算出来的结果满足配合,但是从全网范围来看,动作时间可能会比较长,影响了全网保护动作的“快速性”。 因此,有必要对其予以优化。将考察对象组成一个集合,以集合总的保护动作时间最短为优化目标,其函数为: (11) 式中:n为集合内元件数,常取为待整定元件数;wi为权重系数,与线路的重要程度成正比,以保证其及周边元件严格完全配合;tRi为保护Ri的动作时间。 3.2曲线参数约束条件 鉴于反时限过流保护的曲线特性,其动作方程中各参数均应考虑其限值,优化计算中必须满足式(2)及下式: (12) (13) 式中:tmin为断路器固有时间,常取0.02 s。 3.3选择性配合约束条件 将上节所述选择性分析作为保护配合的约束条件,具体为。 (1) 若上下级保护均为一般反时限,则取式(5)为约束条件。 (2) 若为反时限与定时限保护配合,则取式(6)-(8)及衍生逻辑步骤作为约束条件。 (3) 若为定时限与反时限保护配合,则取式(9)-(10)及衍生逻辑步骤作为约束条件。 3.4优化算法 本文采用在优化领域具有一定优势的粒子群优化算法[15](PSO)对保护定值进行优化。该算法中,每个粒子代表D维空间的一个潜在可行解,以一定速度飞行,并根据自身历史最优位置与群体历史最优位置进行动态调整。第i个粒子当前位置与速度分别记为Xi=(xi1,xi2,…,xiD)与vi=(vi1,vi2,…,viD),该粒子自身历史最优位置与群体历史最优位置分别记为Pi=(pi1,pi2,…,piD)与Pg=(pg1,pg2,…,pgD)。鉴于压缩因子K有助于保证PSO算法收敛,且不需使用最大速度(vmax)[16-17],故本文采用压缩因子粒子群算法(K-PSO),具体方程为: (14) 为验证本文所述方法的正确性及可行性,以图5所示某220 kV电网局部区域进行保护整定计算及定值优化,具体参数(标幺值)见表1,其中X1为正序电抗,Xs表示外部电网等值电抗。短路电流见表2,其中Ikcmax、Ikmax及Ikmin分别为保护正向出口故障流过保护最大短路电流、保护所在线末故障流过保护最大及最小短路电流。保护R8与R10为定时限保护(电流定值依据现有规程整定),其余为带方向反时限保护;式(2)中最大负荷电流IL.max取700 A,式(11)中权重系数wi取1。 图5 电力系统拓扑 名称XsAXsDL1(L2)L3L4L5X1000930011400562002390056000817 表2 短路电流 A 计算详细结果见表3,其中tH、tT分别为保护正向出口故障、保护所在线末故障时的保护动作时间。采用前述保护配合整定原则计算得到定值见表3“优前”,满足了保护配合的选择性要求;在其基础上融入粒子群优化算法进行优化。初始种群数设为100,优化目标为式(11),约束条件见3.2与3.3节,进行优化计算后得到一组可行定值解见表3“优后”。考虑到tT对保护时间影响更大,故式(11)中tRi取为tT。对比可知优化前,时间总和∑(tH+tT)=20.624 s;优化后:∑(tH+tT)=17.865 s。尽管优化后tH稍有增加(6%),但tT下降幅度更大(18%),整体动作时间降低2.759 s(降幅13%)。灵敏性方面,Klm为保护在本线路末端故障时的灵敏度;(+)、(-)分别表示优化前后灵敏系数提高和降低。通过计算Klm可知,虽然保护灵敏度各有提高(R3、R6、R7)与降低(R1、R2、R4、R5、R9),但是前者优化前灵敏度较低(最低值为1.21),已接近规程要求的下限,故优化后对前者灵敏度的提高具有更重要的意义。因此,本算例验证了本文所述方法在满足选择性并兼顾灵敏性的同时提升了全网保护快速性的目标。 表3 整定及优化结果 分析整定配合过程及优化计算可发现,本文所述方法的优势在于:①明确提出了反时限保护与其他定时限保护整定配合原则,一旦将其融入整定计算软件实现自动整定,便可弥补目前手工计算或简化处理反时限保护的短板;②整定计算过程计及优化算法后,则整体动作时间降低,在满足选择性的同时提升了快速性。 本文从保护选择性角度详尽地分析反时限保护之间配合、反时限与定时限保护配合的整定原则,在其基础上从快速性角度建立了优化模型,并以算例进行了相应测试与验证。鉴于目前利用整定软件实现反时限保护自动整定鲜有报道,故在以下方面可进一步开展深入研究:本文仅分析常见的反时限与其他保护配合原则,未计及特殊情况的处理,如T接线、串补线等;本文仅部分利用整定软件,完全实现整定软件自动整定,则需与软件厂家密切配合,深入研究;优化算法融入整定软件,则需进一步完善算法本身及软件接口交互处理等。 [1]ABDELAZIZ A Y, TALAAT H E A, NOSSEIR A I, et al. An adaptive protection scheme for optimal coordination of overcurrent relays[J]. Electric Power Systems Research, 2002, 61(1): 1-9. [2]陶冶,田鹏飞. 辽宁电网零序电流反时限保护速动性分析[J]. 东北电力技术, 2012,33(12): 34-36. [3]张全有. 电动机反时限过流保护模型的分析与算法实现[J].安徽工程大学学报, 2014,29(3): 65-67. [4]王育学,尹项根. 基于能力曲线最优拟合的大型发电机反时限保护研究[J].广东电力, 2014,27(11): 71-76. [5]黄文焘,邰能灵,杨霞. 微网反时限低阻抗保护方案[J]. 中国电机工程学报, 2014, 34(1): 105-114. [6]许偲轩,陆于平,王业. 基于边电压的反时限微网保护方案[J].电力系统自动化, 2014,38(1):68-73. [7]郭煜华,姜军,范春菊,等. 改进的配电网反时限过电流保护[J].电力自动化设备, 2015,35(10):45-50. [8]刘玉,李季英. 含分布式电源配电网的改进反时限过电流保护算法[J].吉林电力, 2014,42(5):12-15. [9]顾志飞,江卫良,郝后堂,等. 一种微机型反时限过激磁保护的实现方法[J].电力自动化设备, 2012,32(7):149-153. [10]吴麟琳,黄少锋.平行双回线对反时限零序电流保护的影响及改进算法[J].电网技术, 2013,37(3): 707-712. [11]韦嘉,柏瑜,熊兰,等. 反时限过流保护模型优化与曲线交叉研究[J]. 电测与仪表, 2015,52(9): 56-60,63. [12]赵黎丽,高昌培,林虎.线路和变压器零序反时限保护及其整定配合[J].电力系统自动化, 2011,35(17):107-110. [13]黄超. 计及风险的继电保护在线校核研究[D]. 武汉:华中科技大学, 2012. [14]侯计兵. 电力系统反时限过流保护优化整定计算研究[D]. 武汉:华中科技大学, 2011. [15]刘顺桂,朱正国,丁庆. 基于粒子群算法的微网保护装置位置优化[J]. 电力系统及其自动化学报, 2015,27(S1): 54-58. [16]张成兴. 压缩因子综合信息粒子群算法[J]. 计算机科学与探索, 2014,8(4): 506-512. [17]王晓佳,张宝霆,徐达宇. 含有压缩因子的粒子群优化灰色模型在智能电网中的应用[J]. 运筹与管理, 2012,21(3): 114-118. Research on Optimal Coordination of Inverse-time Overcurrent Protection HUANG Chao, YANG Yan, TIAN Junyang (Guangxi Electric Power Dispatching and Control Center, Nanning 530023, China) The inherent advantage of the inverse-time overcurrent protection which can closely reflect the change of the short-circuit current is concealed due to the difficulties of the curve coordination, so its application is limited to some extent. Therefore, on the basis of thorough analysis with the strict coordination between protection curves, the setting principles of the coordination between inverse-time overcurrent protection and definite-time protection are presented in this paper with the selectivity of protection being taken into account. And using particle swarm optimization algorithm with constriction factor(K-PSO) accompanied by constraint conditions, such as the curve parameters and selective cooperation, the time-optimization target based on the calculation range of protection setting is built from the perspective of rapidity under the premise of high sensitivity. The setting principles and optimization model can be used for protection setting calculation and setting optimization of inverse-time overcurrent protection respectively, which is helpful for improving the domestic practical value for engineering application. The validity and feasibility of this method are verified through the example. inverse-time overcurrent protection; protection coordination; selectivity; setting optimization; particle swarm optimization algorithm 2016-06-04。 黄超(1987-),男,工程师,研究方向为电力系统继电保护整定计算及定值优化,E-mail:huang_c.dd@gx.csg.cn。 TM771 ADOI:10.3969/j.issn.1672-0792.2016.10.003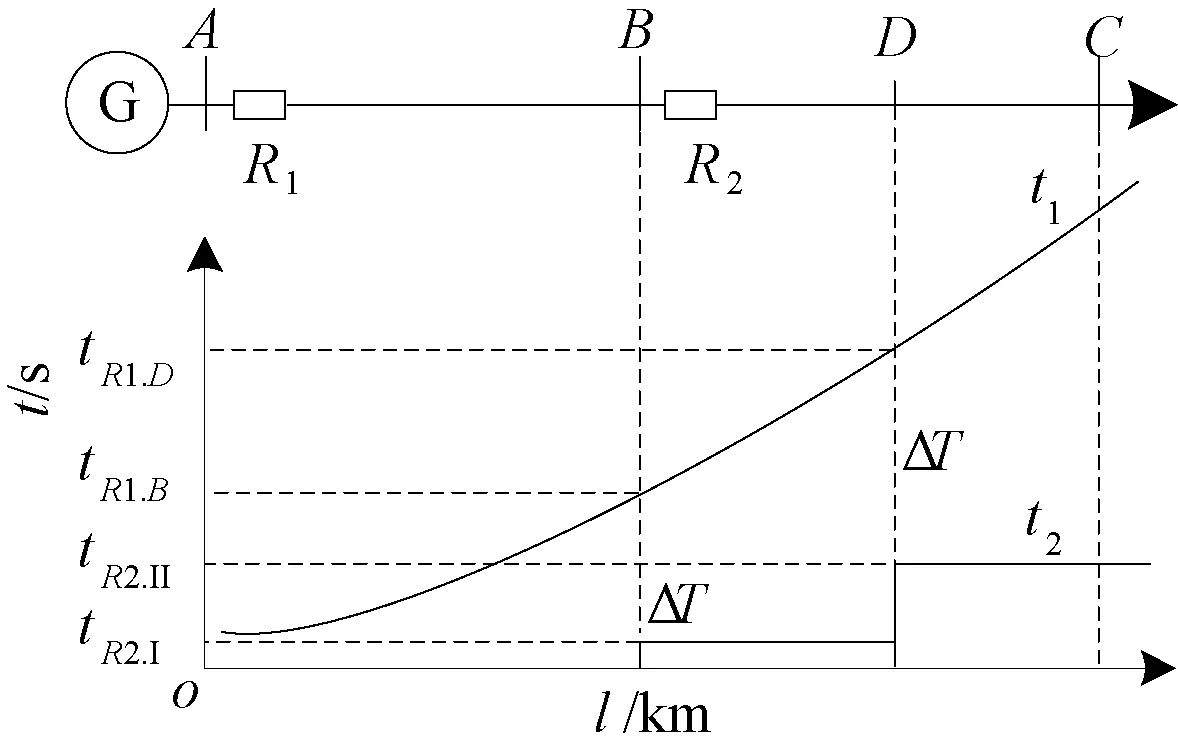
3 反时限过流保护快速性分析及优化模型
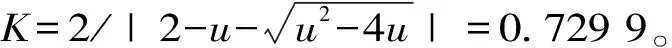
4 算例

5 结论
