基于储能调度模式的分布式光伏两阶段多目标就地消纳模型
2016-11-11华浩瑞
李 鹏,华浩瑞
(新能源电力系统国家重点实验室(华北电力大学),河北保定071003)
基于储能调度模式的分布式光伏两阶段多目标就地消纳模型
李鹏,华浩瑞
(新能源电力系统国家重点实验室(华北电力大学),河北保定071003)
随着分布式光伏接入配电网容量的提高,分布式光伏就地消纳模型成为日益重要的课题。提出了一种基于储能调度模式的分布式光伏两阶段多目标消纳模型。该模型以储能调度策略为主要控制变量并配合机组出力,以分布式光伏消纳率最大为优先目标,以系统运行成本最小为次要目标,计及储能运行约束等必要约束条件。针对建立的模型采用JAS算法配合分段线性化的混合整数规划,并结合智能单粒子算法构成的混合算法进行求解。通过一个算例验证了该模型能在不同渗透率情况下最大化光伏消纳率的同时最小化运行成本,使得模型更加符合实际和具有应用价值。
储能调度模式; 两阶段优化;多目标;光伏消纳;JAS算法;智能单粒子算法
0 引言
2015年3月,《国家能源局关于下达2015年光伏发电建设实施方案的通知》出台,要求全年新增光伏电站建设规模达17.8 GW,并优先建设35 kV以下、20 MW 以下的接入配电网的分布式光伏电站项目[1]。根据中国光伏资源分布特点,未来中国光伏发电发展将呈现大规模、高集中的开发趋势[2]。而随着分布式光伏发电接入容量的提高,研究配电网光伏消纳能力及提高光伏消纳能力的措施具有重要的现实意义[3-5]。
从系统的角度看,不同的电力系统对分布式光伏出力的接纳能力并不相同。面对这样的情况,如果系统有充足的储能设备,则光伏的输出相对容易充分消纳,可更容易实现对光伏输出的平稳消纳而且能够满足系统的安全稳定需求,从而提高光伏的消纳能力。文献[6]基于某一实际系统馈线,结合当地实际负荷及光伏规划容量,利用随机场景方法,分析了系统馈线的最大光伏消纳能力;文献[7]针对大规模并网光电消纳容量计算问题,构建了一种考虑网络传输约束的消纳分析模型;文献[8]制定了以分布式光伏消纳最大化为目标的主动负荷需求响应方案。此外,还有文献[9-10]针对地区特点建立模型计算了其光伏消纳容量。然而,当分布式光伏渗透率较低的情况下,传统的仅以光伏消纳率最高为目标的消纳模型得出的最优解通常不是唯一的,这是因为此时消纳率容易达到100%,而且无法计及含分布式光伏配电网的运行效益。因此需要重新建立模型并在模型中计及其他目标,使得模型更加合理和符合实际。
分布式光伏的渗透率定义为光伏1 d出力总容量与本区域1 d负荷容量的比例。分布式光伏集群相对于电力系统的不同渗透率为就地消纳带来了不同的挑战,本文讨论了光伏渗透率低与渗透率高这两种情况。
本文主要考虑采用储能调度模式提高分布式光伏消纳率并提高含分布式光伏配电网的运行效益,提出一种分布式光伏集群两阶段多目标优化消纳模型。该模型包含优先目标(光伏消纳率最大)和次要目标(系统运行成本最小)。事实上,该模型存在一个分布式光伏边界渗透率,当光伏渗透率较小于该边界渗透率的情况下,优先目标容易达到上限,因此需要模型以运行成本最小为目标,系统的安全较易保证,备用需求相对较小,因此储能单元的作用主要还是提供合理的热备用与调峰能力,并在一定程度上实现削峰填谷;当光伏渗透率大于该边界渗透率的情况下,储能是备用的重要组成部分,优化的重点是保证安全,通过合理的储能调度实现光伏尽可能多的安全消纳,此时希望模型主要考虑优先目标。
然而,在实际运行中,难以判定边界渗透率,而传统优化模型无法自动地针对任意情况对该两阶段消纳模型进行求解。因此本文提出了基于JAS算法的两阶段多目标优化消纳模型求解方法。通过算例表明,本文模型可以自动地在优先实现最大化光伏消纳率的同时,尽量满足系统运行成本最小。
1 储能调度模型
本文根据分布式光伏渗透率针对2种情况进行分析:
第1种情况,分布式光伏渗透率较低。此时光伏功率输出的随机性与不确定性相对较小,系统有足够的能力对这些不确定性因素加以消纳,因此带来的负面影响较易消除。此时可以将整体经济性作为优化目标,在保证网络安全的情况下做到光伏输出的几乎100%就地消纳,同时实现经济性的最优化。之所以不能完全做到100%是因为在分钟甚至秒级的时间尺度上可控机组的爬坡率限制以及储能出力变化速率限制。主要思路是首先令光伏集群以最大功率点跟踪(Maximum Power Point Tracking, MPPT)模式全额输出,其余发电单元配合储能,在光伏达到最大消纳的基础上,通过合理的调度计算,以综合经济性的最优为目标实现包括经济性等多目标的整体的优化。
第2种情况,分布式光伏渗透率较高。此时的特点是需要一定的优化才能做到光伏充分消纳,同时也可能有余力对经济性进行一定的优化。光伏较大程度的不确定性成为了消纳率提升的最大障碍,因为这样的问题很可能导致安全约束、系统调峰、备用等约束无法满足等问题的出现。因此,在第1种情况下需要以安全可靠为第一要素,此时将根据需要限制部分光伏出力(亦即“弃光”),迫使光伏按给定的要求减少出力以维持安全性和系统稳定,但是这样做会导致能量的损失。考虑到储能相比于火力发电等传统电源来说拥有更高的灵活性,在合理的储能调度优化基础上,可通过对储能运行时间与容量的合理调度,实现减少弃光的目标,从而提高光伏发电的就地消纳能力。
分布式光伏的功率输出曲线和负荷曲线通过日前预测获得。在所研究的电力系统中,除了分布式光伏集群、负荷与储能设备以外还装配有火力发电机组作为可控电源。
系统的目标函数以光伏集群的功率消纳率最高为优先目标,在保证消纳的情况下,兼顾其他目标。首要目标为光伏消纳率F1如式(1)所示。对于所给定的光伏出力预测曲线PPV,0(t),实际消纳为PPV(t),那么在日前计划中的光伏消纳率F1可以通过消纳的光伏功率总和与光伏实际出力总和之比来表示。
(1)
式中:T为总时段数。
两阶段优化模型的次要目标采用多目标模型。次要目标的第1个子目标为经济成本,主要考虑了发电成本如式(2)所示,此外为了计及含分布式光伏接入配电网的节能减排效益,目标函数中还应计及网损成本如式(3)所示,任意时段的网损成本按该时段的外网分时电价水平计算价值,从而与发电成本相整合。
(2)
式中:C1为经济成本;G为总机组数;fg() 为机组g所对应的成本曲线,已经包含了燃料成本、运行维护成本、设备折旧成本等必要成本;Pg(t)为机组g在t时段的出力;ΔT为每个时段对应的时长,本文中取为1 h。
(3)
式中:C2为网损成本;Ploss,l(t)为t时段线路l的网损,总线路数量为L;p(t)为t时段外网分时电价水平。
因此,所构成的第一个子目标经济成本为f1如式(4)所示:
(4)
第2个子目标为储能电量越限惩罚项。一般文献通常直接采用储能电量上下限约束来对储能中电量进行约束从而避免其越限[11]。然而在实际中,在某些情况下允许储能电量越限是有利的,只需要对储能电量越限加入一定的惩罚项计入目标函数即可,但是仍然希望储能电量越限程度越小越好。而这样的模型更加符合实际也具有更好的效益。储能电量越限的目标函数惩罚项,即次要目标的第2个子目标f2如式(5)所示,其中储能电量越限百分比ΔSSB(t)如式(6)所示。
(5)
(6)
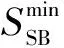
因此,两阶段模型的次要目标如式(7)所示:
(7)
式中: γ1与γ2为权系数。
整体优化模型为,首先满足消纳率最大化目标maxF1,如果在达到100%消纳的情况下,考虑次要目标minF2的优化。当优化模型的优先目标达到最优且最优解不唯一的时候,则最优解在满足优先目标最优的前提下由次要目标对应的优化模型来决定。
所要满足的储能相关的约束条件包括储能充放电功率上下限约束,储能电量与储能充放电功率关系的约束,以及储能首末电量约束。
针对本文项目基于的分布式光伏示范工程所在地区的特点,本文研究中采用的储能单元形式为集中式蓄电池组。所用蓄电池的数学模型为:
储能充电时和放电时的电能模型如式(8)和式(9)所示:
(8)
(9)
式中:PSB(t)为t时段蓄电池功率,以放电为正方向;ηin为充电效率;ηout为放电效率。
此外,蓄电池储能还需要满足充、放电功率上下限约束:
(10)
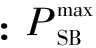
此外,由于本文考虑的是1 d内的消纳模型,为了维持电能稳定以及保证次日的运行调度,需要引入调度周期首末电能约束如式(11)所示;在实际运行中,储能1 d首末电量一般可取为储能容量的一半。
(11)
式中:SSB(0)表示第一时段前的储能电量;SSB(T)表示1 d最后1个时段末的储能电量。本文中储能电量只考察每个时段始末,即1 d 25个时刻的储能电量情况。
在日级时间尺度上的储能运行方式研究中,假定储能的折旧相对较小,因此忽略储能容量的变化对模型的影响。
此外,所需要满足的约束包括机组出力上下限约束如式(12)所示、节点电压约束如式(13)所示、以及联络线传输功率约束如式(14)所示。
(12)
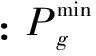
(13)
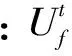
(14)
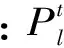
此外,假定该含分布式光伏接入的配电网系统已经向外网购买了必要的旋转备用以应对光伏出力较小时间尺度上的波动性,该购买容量的确定可以通过优化配置模型确定,不是本文研究重点,因此假定该购买的旋转备用是充足的。
2 模型求解算法
上述光伏集群就地消纳问题构成了多个目标的优先级与目标函数值相关联而形成了分阶段的非线性多目标优化问题,该问题不适合用常规的混合整数线性规划方法(常规MILP)加以求解,对此可采用Jump and shift method[12]迭代算法(简称JAS)配合分段线性化的混合整数规划算法,并结合智能单粒子算法(Intelligent Single Partical Optimization,ISP)[13]构成的混合算法求解。
混合算法的主体迭代算法JAS,是一种提高复合型优化问题求解效率的有效方法。设有两个优化问题,分别记为优化问题A:
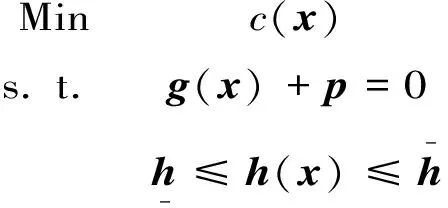
(15)
以及优化问题B:
(16)
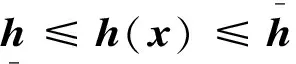
不同于传统的代入求解,JAS算法采用分开计算、循环整合的方式对这两个相互耦合的问题进行整体优化,并且避免了计算量的明显增加;此外,其内部的小范围松弛也为过程中的寻优提供了更多的机会。在JAS方法中定义3组优化变量形成的向量如下:
(17)
式中:F-1(A)|p为在给定的p值下优化所得解x;G-1(B)|x为在给定x的基础上优化所得解y;K-1(B)|x为给定x的基础上优化所得解p。这一通过求解优化子问题而获得适用于另一问题的优化变量值的过程被称为Jump过程。
同时,定义如下的Shift因子χ用于调节算法的收敛速度:
(18)
式中:x(i)为第i个变量;x(i)new为在χ的限制下所得的新x(i)值。
基于JAS可实现分阶段多目标的优化计算。整体方法为建立计及光伏消纳率最大化与综合经济性最优的分阶段目标,构建多目标优化运行复合问题,其中优先考虑光伏消纳率最大化;在首要目标得到满足的情况下,以其保持最大为约束条件、以次要目标为优化目标进行第二阶段的优化计算。
混合整数规划MILP可以解决的机组组合问题构建为问题A,潮流与损耗优化的部分构建为问题B。其连接关系为:
(19)
式中:G为系统中机组数量;PLD(t)为t时段系统总的净负荷功率,即系统总负荷功率减去光伏发电功率;PLOSS(t)为t时段全系统的损耗。通过潮流计算即可获得网络中包括潮流与节点电压等各项参数,由Shift因子χ松弛后的机组输出功率可在松弛范围内以光伏消纳率进一步提高或损耗最低为目标进行寻优求解工作。
问题B构建为变量搜索范围有限的优化问题,采用智能单粒子算法ISPO实现快速求解。ISPO只需要在一个粒子的基础上通过特殊的迭代循环实现优化求解,寻优准确,计算快速。
将ISPO算法用于求解问题B,则优化变量为某个静态时间断面下各单元的出力情况,其变量约束除设备本身以外,还受到Shift因子χ的限制。
看到卢一平语噎,郝桂芹转身走了。走几步,回头又说。你再想想,将来你儿子去城市买房,开发商用杂志和你结算吗?
在ISPO中定义了“子矢量”的概念。称用矢量表示的解为“解矢量”,即静态时间断面下的矢量p,则子矢量为这个解矢量的片段,具体含义为若干机组的出力组合。ISPO算法的唯一粒子是整个解矢量,维数为D,可划分为m个互不重叠的片段,则称将解矢量分解为m个子矢量。每一个子矢量都拥有自己的位置zj与速度vj,j=1,…,m。子矢量的划分取决于按照变量之间的关联,关联紧密的变量在划分到同一子矢量后,寻优能力通常会更强。每一片段允许不连续,但这实际上等价于对变量进行某种重新排列,因此为了叙述简单起见,这里依然用子矢量连续的形式表示。
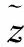
(20)
(21)
(22)
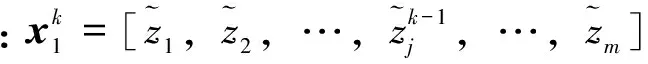
3 求解方法流程
算法的流程为:
(1)以光伏就地消纳率最大为目标,以系统和设备限制为约束,对问题A进行MILP机组组合计算,并将出力计划送入问题B。
(2)问题B中在Shift因子χ范围内,通过ISPO计算损耗并修正平衡等式,在变量优化范围内以光伏就地消纳率最大为目标进行寻优。
(3)如果光伏消纳率已经达到最大,则修改模型,加入保持光伏消纳率最大的约束和综合经济性最优的目标,进入步骤4;否则如果不满足收敛条件,就重复步骤1;若光伏消纳率还没有达到100%但已经达到收敛条件,则转步骤7。
(4)以综合经济性最优为目标,在保持光伏消纳率最大的基础上对问题A进行MILP机组组合计算,并将出力计划送入问题B。
(5)问题B中在Shift因子χ范围内,通过ISPO计算损耗并修正平衡等式,在变量优化范围内以综合经济性最优为目标进行寻优。
(6)如果综合经济性最优的计算已经收敛,则转步骤(7);否则转步骤(4)。
(7)停止计算,输出结果。
4 算例
本文基于IEEE九节点系统构建了改进的含分布式光伏接入的系统。在算例中有3台发电机组分别为Gen1、Gen2、Gen3分别接入节点1、2、3,容量依次为400 MW,400 MW,200 MW,其中节点1通过PCC与外网连接,可以由外网向该含分布式光伏的配电网传输功率,为了保证外网的安全可靠性,因此不考虑节点1通过PCC向外网售电的情况。在负荷节点5、6、8分别接入分布式光伏,接入容量相等,接入总容量在具体算例中根据要考察的渗透率而定;在节点9接入集中式储能系统蓄电池组,其配置容量为250 MW·h,充放电功率上限50 MW。本文主要研究分布式光伏有功功率的消纳模型,因此假定系统中无功功率充足而不考虑无功运行特性。
算例1:光伏渗透率较低的情况。分布式光伏集群的总容量为250 MW,渗透率为20%。备用容量取负荷的10%及光伏计划的20%,且不考虑机组检修和突发性误差等问题。系统中光伏预测曲线PV与负荷预测曲线PL如图1所示。
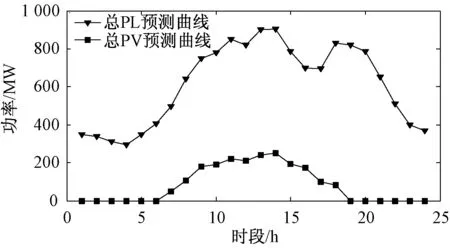
图1 算例1低渗透率时负荷与光伏预测
采用本文的储能调度模式进行求解,可以得到结果该算例中可以做到光伏100%消纳,因此求解方法中的优化目标自动调整为综合经济性即次要目标。在不使用储能的情况下,全调度周期的综合成本为106 858.7元,光伏就地消纳率100%;在加入储能的情况下,全调度周期的综合成本为103 357.7元,光伏就地消纳率为100%。这种情况下,模型的优先目标消纳率最高,容易得到满足且满足时的最优解不唯一,因此模型按照次要目标运行成本最小进行优化调度。
在算例1中,储能主要作用是小额度的削峰填谷,由于火电机组的燃料成本曲线的斜率随着其出力的增大而增大,因此通过储能的削峰填谷作用可以让机组尽量运行在效率较高的低斜率部分,从而降低运行成本。事实上,算例1中综合成本降低了3.3%,各机组以及储能充放电状况如图2所示。
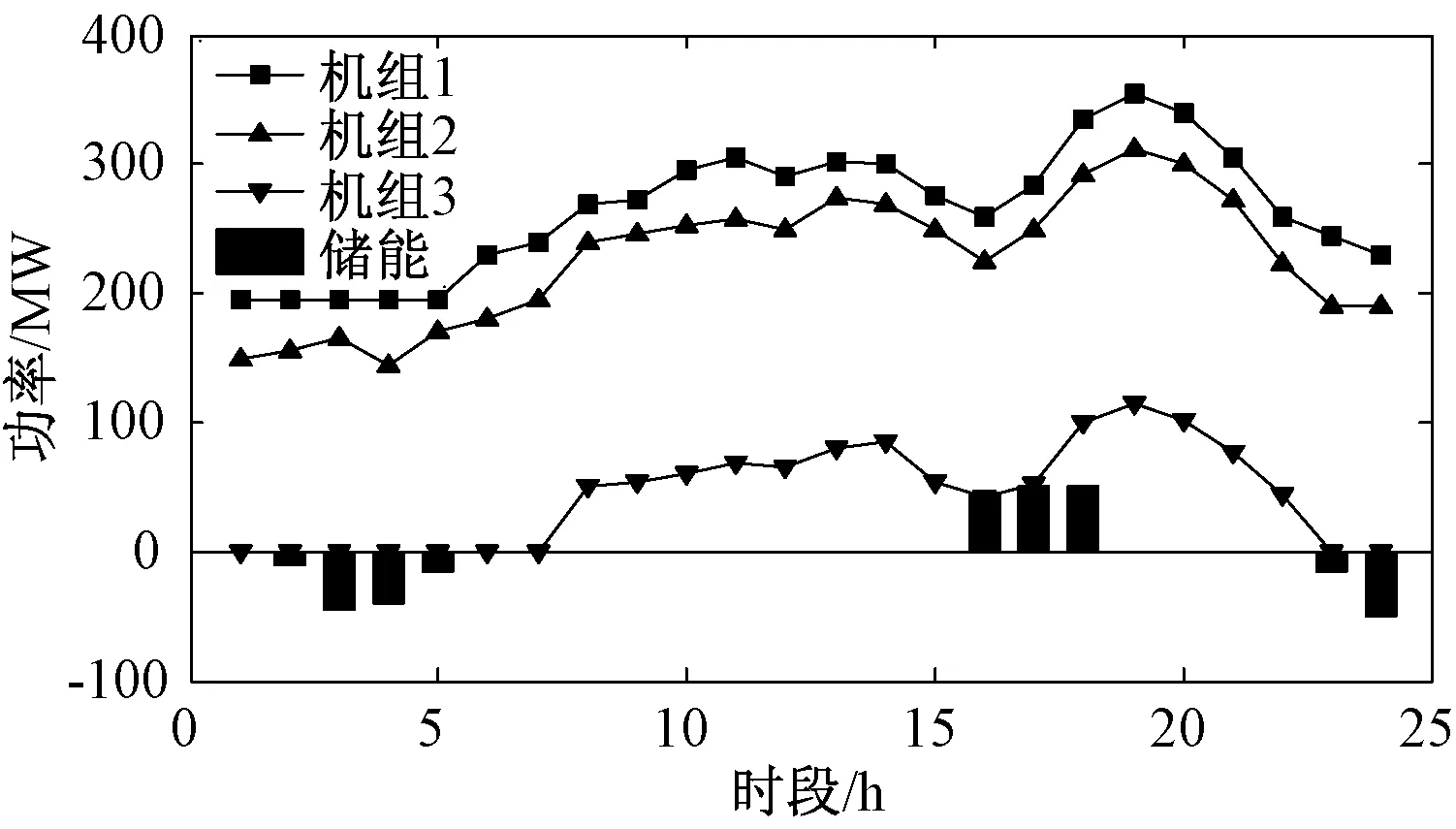
图2 算例1消纳光伏策略
算例2:同算例1,只按比例改变光伏的总装机容量,将其提高到875 MW,此时渗透率为70%,这个数据意味着在光伏输出高峰时对其他发电单元有明显的替代效果。高渗透率下系统中光伏预测曲线PV与负荷预测曲线PL如图3所示。
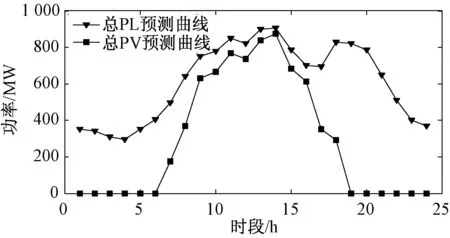
图3 算例2低渗透率时负荷与光伏预测
在不使用储能的情况下光伏消纳率为98.17%,综合成本为65 177.83元;使用储能的情况下,光伏消纳率提高到100%,综合成本为63 831.52 元。可以看出,储能的合理调度实现了光伏就地消纳率的提升,将本来难以消纳的部分也得以充分利用,光伏消纳率提高了1.83%,实现了就地充分消纳;综合成本降低了2.06%,相比之下效果没有光伏渗透率较低的情况更显著,这是因为当分布式光伏渗透率较高时,可以大大降低机组出力,使得机组更倾向于运行中燃料成本曲线的高效率部分,而使得通过储能进一步提高效率的空间相对有限,所以通过储能削峰填谷的成本下降效益没有算例1显著。
在这种情况下,模型按照优先目标进行优化调度,当优先目标既光伏消纳率达到最大时,此时优化运行结果唯一;事实上,算例2中的各机组出力曲线以及储能充放电状况如图4所示。
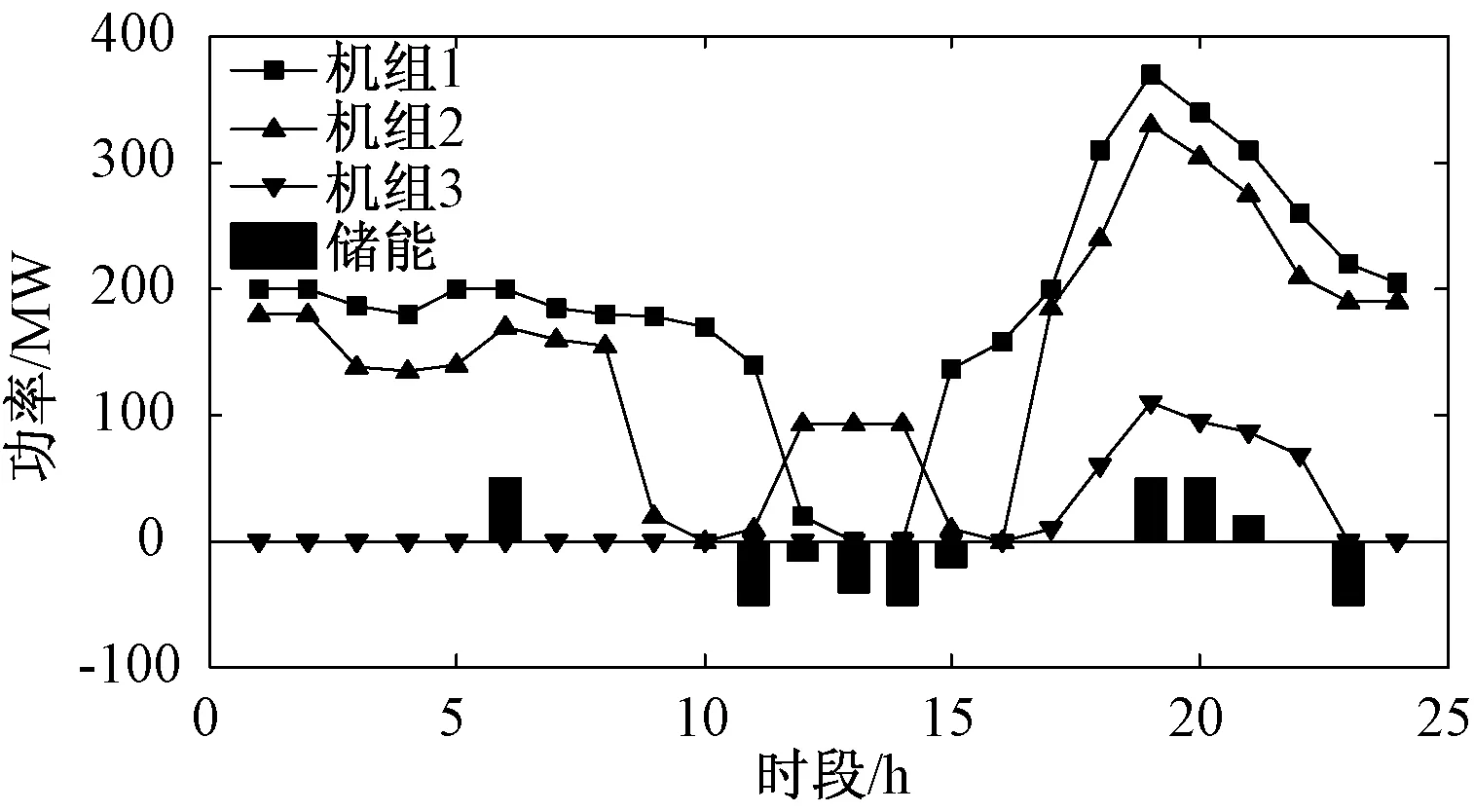
图4 算例2消纳光伏策略
具体分析储能的作用可以看出,在光伏高峰阶段储能主要是吸收能量,而在晚上负荷小高峰但光伏无输出的情况下,储能放电,实现了光伏功率的更充分利用,整体满足合理利用的要求。在本文2个算例中,储能的1 d各时段电量情况如图5所示。在算例1中,储能的作用主要是削峰填谷,因此其电量在负荷高峰时期较低;而在算例2中,储能调度的主要目的是提高光伏消纳率,因此在光伏大量并网时充分充电,其电量在光伏出力大时较高。
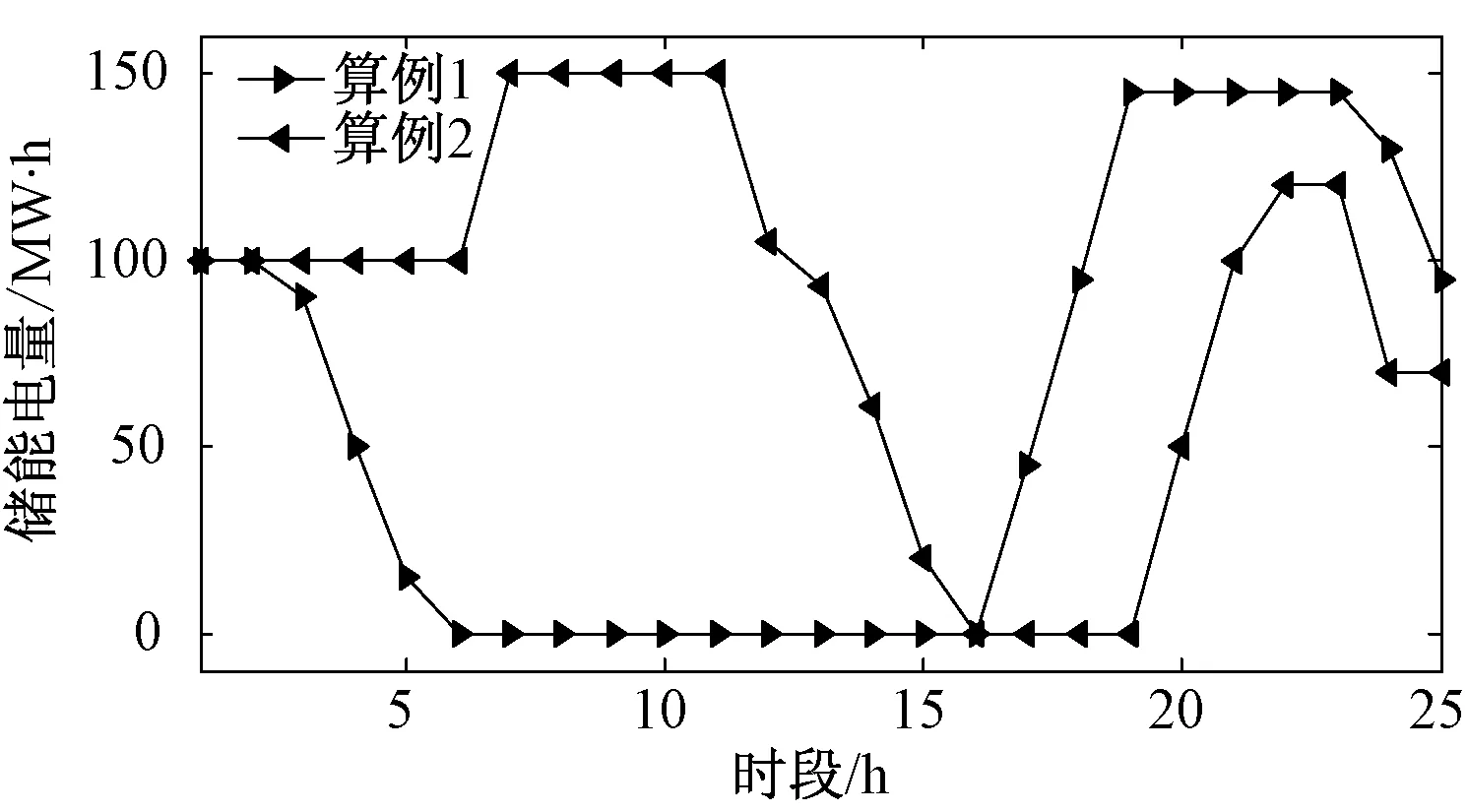
图5 算例1和算例2的1 d各时段储能电量情况
5 结论
本文提出了一种基于储能调度模式的分布式光伏集群两阶段多目标优化消纳模型。本文模型可以在优化光伏消纳率的同时,更好地兼顾系统运行成本最小化的目标。通过算例说明:
(1)在分布式光伏渗透率较高时,采用本文储能调度模式相比于不采用储能调度模式时,可以较好地提高光伏消纳率。
(2)当分布式光伏渗透率较低的情况下,采用储能调度模式对分布式光伏消纳率的提升没有显著作用,当满足优先目标最优时的最优解不唯一,此时模型可以自主地计及次要目标即系统运行成本最低,制定经济的调度策略。
(3)当分布式光伏渗透率较高的情况下,模型自主地以优先目标即消纳率最大为目标,采用储能调度模式对分布式光伏消纳率的提升有显著作用。
(4)提出的混合智能算法使用于求解类似本文的两阶段多目标优化模型,具备较好求解效果。
[1]刘皓明,陆丹,杨波,等. 可平抑高渗透分布式光伏发电功率波动的储能电站调度策略[J]. 高电压技术,2015,41(10): 3213-3223.
[2]白建华,辛颂旭,贾德香,等. 中国风电开发消纳及输送相关重大问题研究[J]. 电网与清洁能源,2010,26(1):14-17.
[3]孙卓新,朱永强,倪一峰,等. 基于粒子群算法的含光伏电站的配电网无功优化[J]. 电力建设, 2014, 35(4) : 25-30.
[4]陈炜, 艾欣, 吴涛, 等. 光伏并网发电系统对电网的影响研究综述[J]. 电力自动化设备, 2013, 33(2): 26-32.
[5]魏磊, 姜宁, 于广亮, 等. 宁夏电力系统接纳新能源能力研究[J]. 电网技术, 2010, 34(11): 176-181.
[6]赵波,韦立坤,徐志成, 等. 计及储能系统的馈线光伏消纳能力随机场景分析[J]. 电力系统自动化, 2015,39(9):34-40.
[7]欧阳聪,刘明波. 考虑网络传输约束的并网光伏发电消纳容量计算[J]. 电力系统保护与控制,2016,44(5):17-23.
[8]汤奕,鲁针针,伏祥运. 居民主动负荷促进分布式电源消纳的需求响应策略[J]. 电力系统自动化,2015,39(24):49-55.
[9]姚天亮,郑海涛,杨德洲,等. 甘肃河西500万kW光伏就地消纳及调峰分析[J]. 中国电力,2014,47(3):14-18.
[10]宁光涛,谢海鹏,别朝红,等. 海南电网分布式光伏消纳能力评估[J]. 南方电网技术,2015,9(5):59-65.
[11]桑丙玉,王德顺,杨波,等. 平滑新能源输出波动的储能优化配置方法[J]. 中国电机工程学报,2014,34(22):3700-3706.
[12]CHEN S X, GOOI I H B.Jump and shift method for multi-objective optimization[J]. IEEE Transaclions on Industrial Electronics, 2011, 58(10): 4538-4548.
[13]纪震,周家锐,廖惠连,等.智能单粒子优化算法[J].计算机学报,2010,33(3):556-561.
Two-stage Multi Objective Consumption Model for Distributed Photovoltaic Based on Energy Storage Scheduling Mode
LI Peng, HUA Haorui
(State Key Laboratory of Alternate Electrical Power System With Renewable Energy Sources,North China Electric Power University, Baoding 071003, China)
With the increase of the distributed photovoltaic (PV) capacity connected to distribution network, distributed photovoltaic consumption model has become an increasingly attractive topic. This paper proposed a two-stage multi-objective consumption model for distributed PV based on energy storage scheduling mode. The proposed model uses energy storage scheduling strategy, combining with the unit output as the main controllable variables, while the maximizing consumptive rate of PV is considered as the priority target and minimizing operation costs as the secondary one. The constraints include energy storage operation conditions, etc. For the built model, this paper uses JAS algorithm combined with mixed integer programming with piecewise linearization, and the intelligent single particle algorithm is applied to solve the subsequent mathematical problem. Last, an example is made to verify the proposed model. It comes out that the proposed method can maximize consumptive rate of PV at the same time minimize operation costs in conditions of different PV penetration rate, which makes the model more practical and useful.
energy storage scheduling mode; two-stage optimization; multiple objective; consumption of PV; JAS algorithm; intelligent single particle algorithm
2016-07-05。
国家电网公司总部科技项目 (520201150012)。
李鹏(1965-),男,教授,主要研究方向为新能源并网发电微网技术、电能质量分析与控制、电力电子技术在智能电网中的应用等,E-mail:ncepulp@gmail.com。
TM615
ADOI:10.3969/j.issn.1672-0792.2016.10.001
