星级复杂系统的可靠性参数

张其斌，沙孝聪，王　娜，徐惠萍，马　骥

（1.甘肃省计算中心，兰州　730030；2.兰州大学 计算机科学与技术系，兰州　730030）

星级复杂系统的可靠性参数

张其斌1，沙孝聪2，王娜1，徐惠萍1，马骥1

（1.甘肃省计算中心，兰州730030；2.兰州大学 计算机科学与技术系，兰州730030）

在减少复杂子系统线性组合的系统复杂性中，可靠性参数扮演着非常重要的角色.本文定义了一种新的复杂系统，即star-k-out-of-n：F系统，而且同时计算了这个系统的可靠性参数.

可靠性参数；复杂系统；star-k-out-of-n：F系统

0　引　言

在复杂系统的可靠性分析中，复杂系统的失败一般出现在线性平行系统的合并中.线性合并中的协同因素也就是可靠性参数，是由g（n,i）定义的，这就是

定义1把Fn定义为某个由n个落在［0，t］事件区间的部分组成，q表示在［0，t］区间内每个系统组成部分失败的可能性，而且r表示能造成整个复杂系统失败的最小组成部分失败数.则整个系统失败的可能性公式可以表示为

这样的话，g（n,i）（r≤i≤n）可以被说成是可靠性参数.

Petakos和Tsapelas［1］给出了可靠性参数的性质，而且研究了star-k-out-of-n∶F系统的协调因素，star-k-out-of-n∶F系统是在可靠性学说中最有趣的.Li和Zhao［2］指出g（n,i）独立于时间的，而且仅仅是依赖系统的几何结构.对于其他关于k-out-of-n系统的理论，请参看文献［3-11］.

在这篇论文中，我们介绍了star-k-out-of-n∶F系统，而且研究了可靠性参数.文章的结构是∶第1节介绍可靠性参数的两种性质；第2节展示star-k-out-of-n∶F系统的定义；第3节stark-out-of-n∶F系统的可靠性分析.第4节提供一些数据表来证明这些协同因素；第5节总结.

1　可靠性参数的性质

首先，我们要展示可靠性参数的两种有用的性质（由K.Petakos和T.Tsapelas发现的）.用Z表示系统中失败的组成部分，即有以下两种性质［1］.

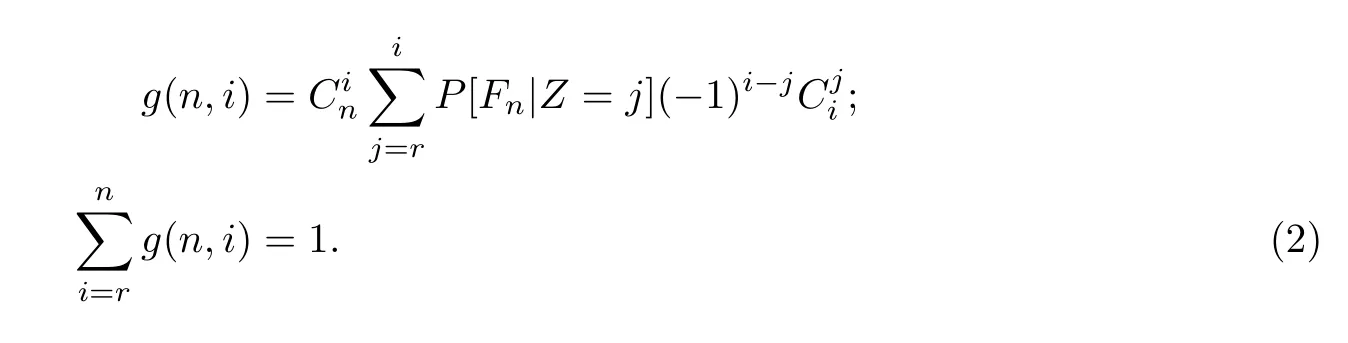
2　Star-k-out-of-n:F系统

在真实的生活中，我们经常遇到的情况是一个主要的组成部分控制系统的运行，而其他的组成部分为次要部分.比如说，在本地的网络结构中，服务器是主要部分，而其他的客户端电脑则是辅助设备.如果服务器奔溃了，那么整个网络就不会工作了.这样的系统，就是我们所知道的star-k-out-of-n∶F系统.

2.1Star-k-out-of-n∶F系统的拓扑结构

在star-k-out-of-n∶F系统中存在一个主要的中心组成部分和n个叶子组成部分.我们用K1,n来表示star-k-out-of-n∶F系统.例如，在图1中展示了K1,4的结构，顶点O是一个中心组成部分，然后其他的定点是叶子组成部分.

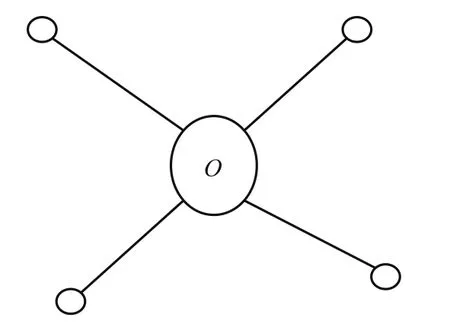
图1　K1,4系统Fig.1　K1,4system

2.2Star-k-out-of-n∶F系统的失败运行机制

在star-k-out-of-n∶F系统中，有两种系统崩溃的例子，分别是由中心组成部分和叶子组成部分的损坏造成的.

情况1∶中心节点崩溃.

情况2∶中心节点未发生崩溃，但是知道有k个叶子组成部分崩溃.

现在给star-k-out-of-n∶F系统下定义.

定义2如果一个系统有2.1部分中的拓扑结构而且有2.2中的失败运行机制，那么它就会被称为一个star-k-out-of-n∶F系统.而且，如果一个系统中所有的组成部分都是独立的，且可靠性都是相同的，那么这个系统就会被称为是一个独立的star-k-out-of-n∶F系统.

3　Star-k-out-of-n:F系统的可靠性分析

在这个部分中，我们将计算star-k-out-of-n∶F系统中的可靠性因子.

通过star-k-out-of-n∶F系统的崩溃机制，最小的可能导致系统崩溃的节点崩溃数r=1.从式（1）中可以知道，所有组成系统的节点数目是n+1，star-k-out-of-n∶F系统的崩溃可能性可以用方程

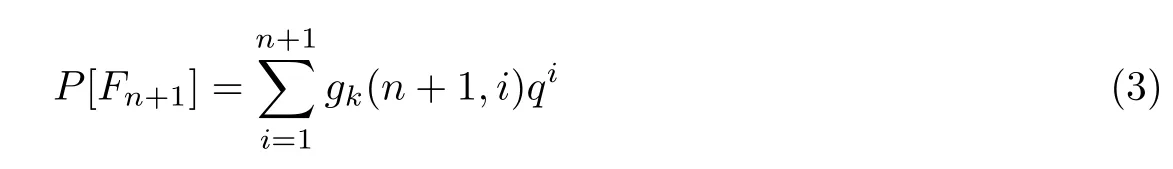
来表示.

同样地，通过式（2）可得

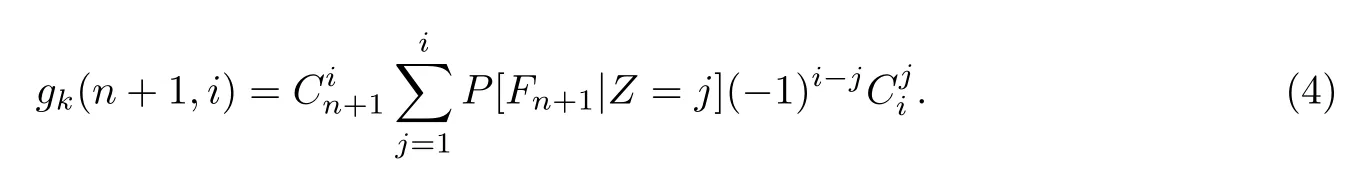
在式（3）和式（4）中，我们用gk（n+1,i）来表示star-k-out-of-n∶F系统的可靠性参数.注意这些依然与参数k有关.

作为本文的主要结果，我们给出定理1和定理2.

定理1独立的star-k-out-of-n∶F系统在某种条件下崩溃的可能性中，所能容忍的节点崩溃数量是

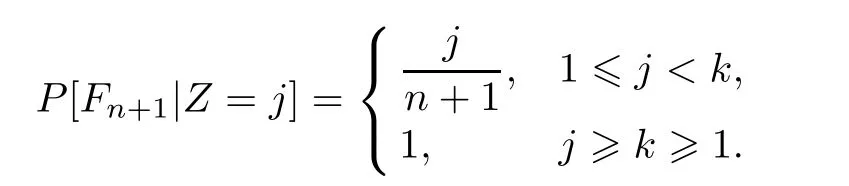
证明很明显，在k=1或j≥k＞1的情况下，P［Fn|Z=j］=1.因此我们只需要考虑1≤j＜k的情况.

通过条件可能性公式

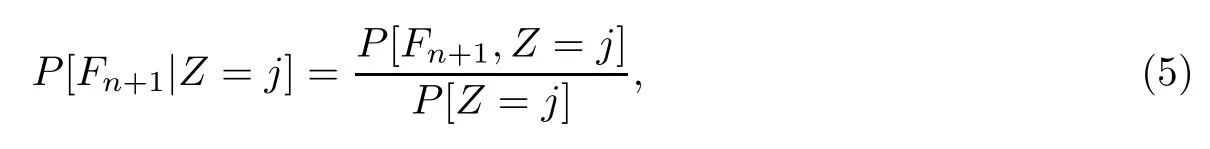
注意到star-k-out-of-n∶F系统中共有n+1个相互独立且失效的概率都为q的节点，所以Z服从参数为n+1和q的二项分布，即

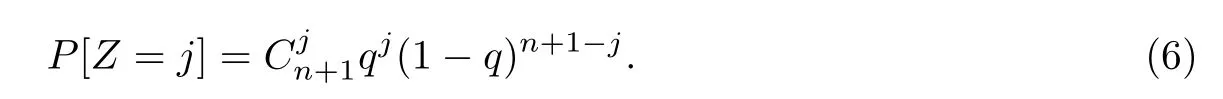
用A表示中心组成部分崩溃，用X表示叶子组成部分崩溃的可能性，有

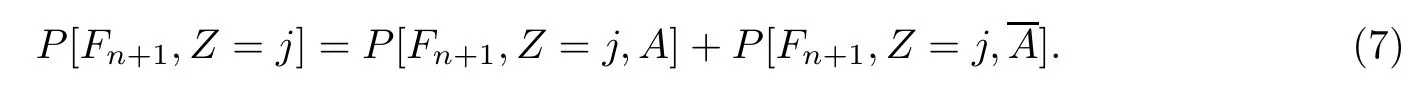
因为j＜k和A并没有发生，所以

除此之外，因为｛Fn+1,Z=j,A｝⇔｛Fn+！,X=j-1,A｝⇔｛X=j-1,A｝，而且注意组成部分是相互独立的，然后

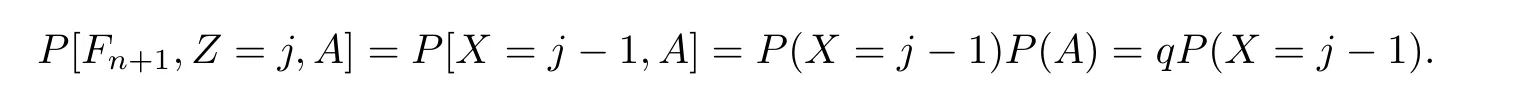
很明显，X服从参数n和q的二项分布，因此

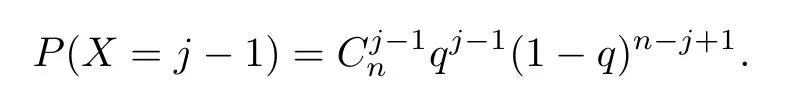
而且因为

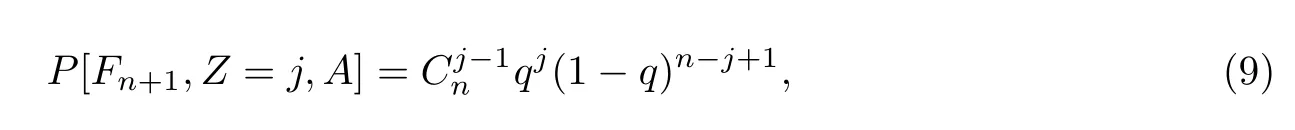
把式（8）和式（9）代入式（7），可得

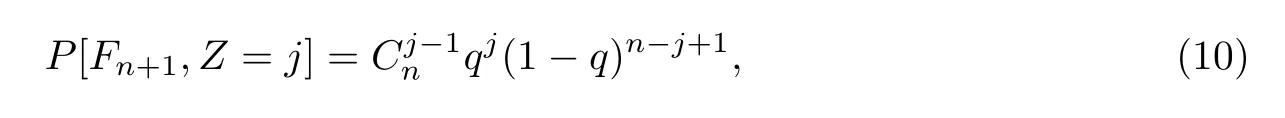
把式（6）和式（10）代入式（5），可得

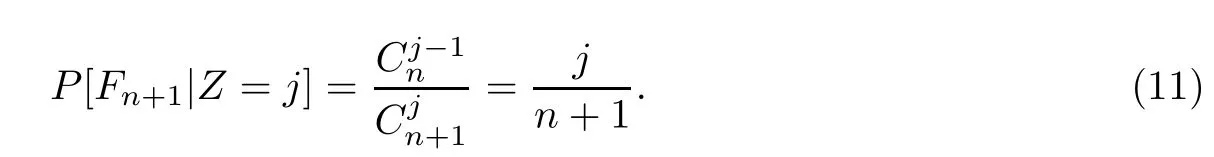
这样的话就有

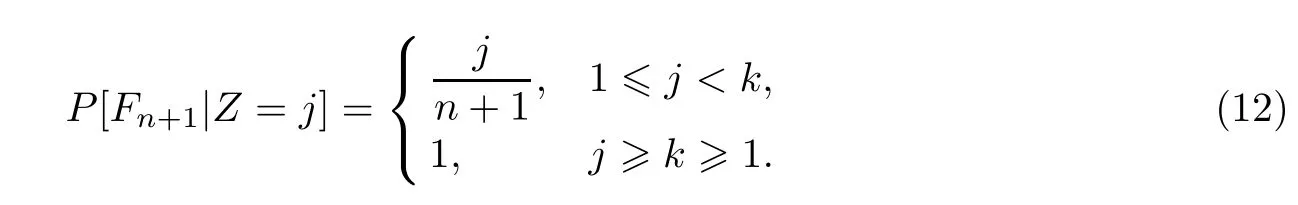
定理1被证明.从定理1，我们可以得到star-k-out-of-n∶F系统的可靠性参数.

定理2独立的star-k-out-of-n∶F系统的可靠性参数方程式为

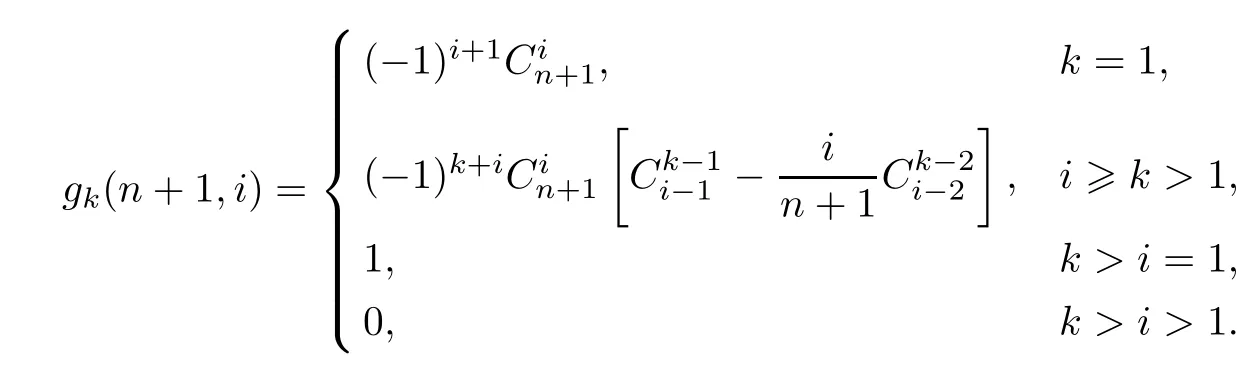
证明把式（12）代入式（4），可得

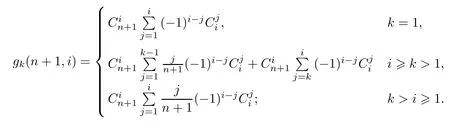
定理2被证明.

4　数值模拟

在这部分中，我们提供很多不同的数据表来证明gk（n+1,i）的价值.表1指的是star-2-out-of-10∶F系统；表2指的是star-3-out-of-10∶F系统，表3指的是star-4-out-of-10∶F系统.

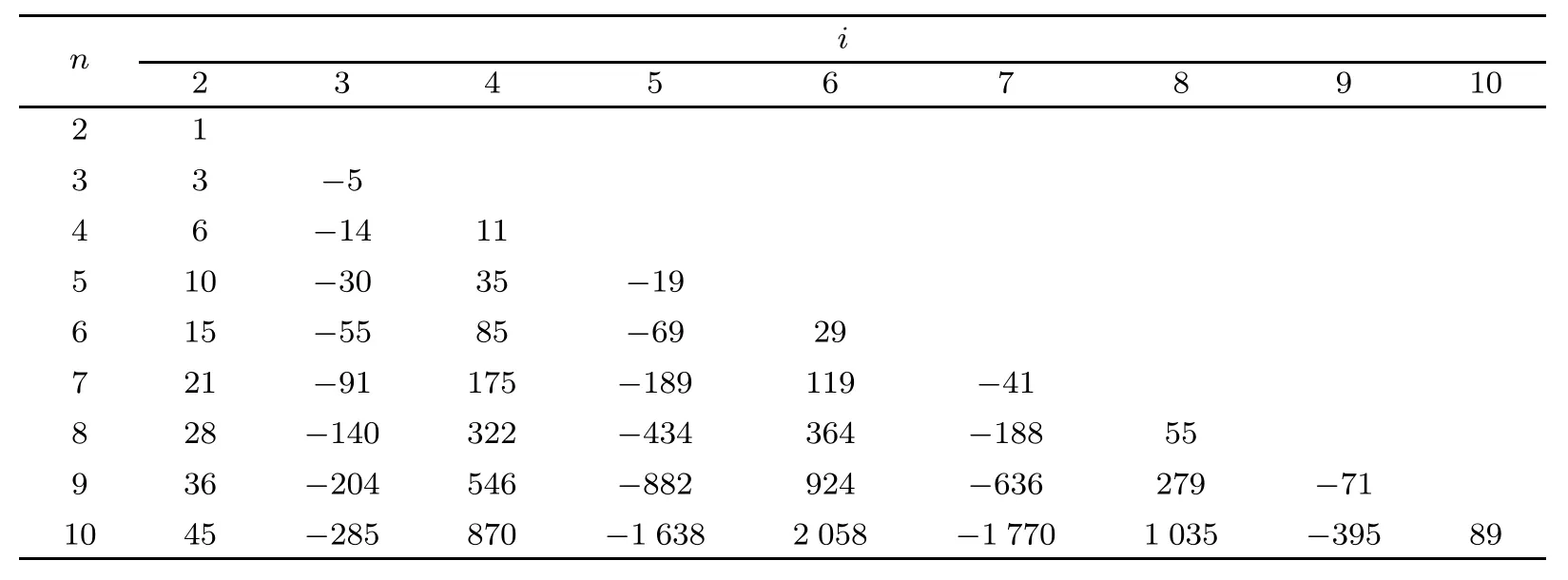
表1　star-2-out-of-10：F系统的相关性参数Tab.1　The reliability coefficients g（n，i）for a star-2-out-of-10：F system

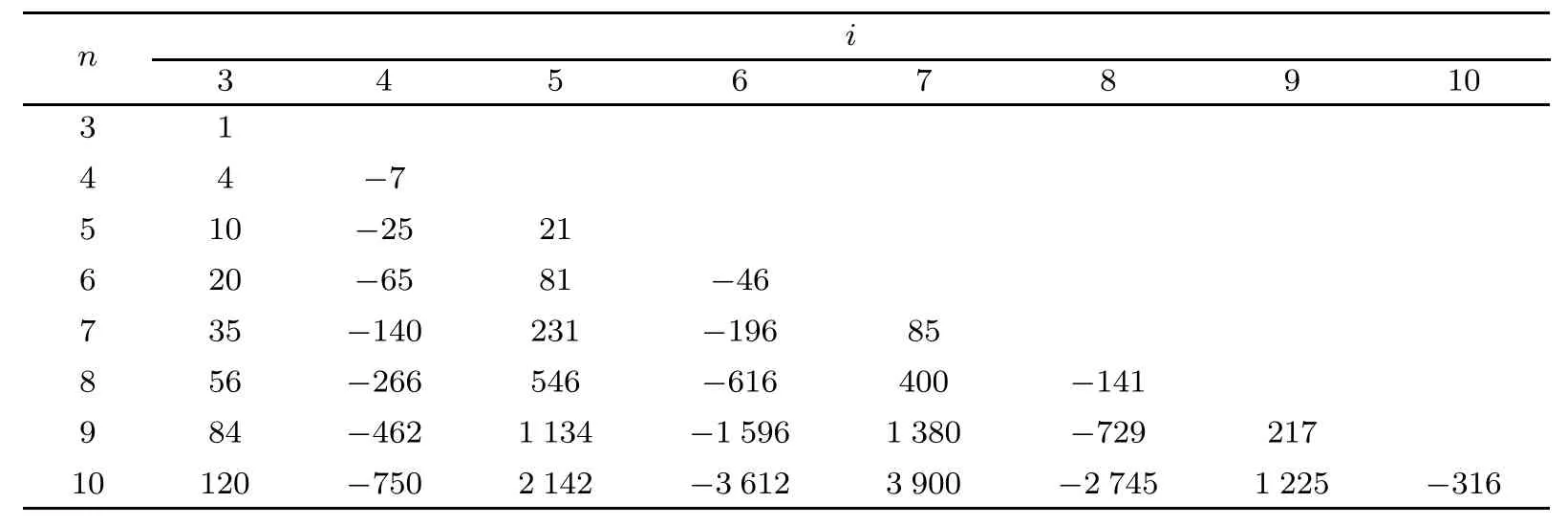
表2　star-3-out-of-10：F系统的相关性参数Tab.2　The reliability coefficients g（n，i）for a star-3-out-of-10：F system

表3　star-4-out-of-10：F系统的相关性参数Tab.3　The reliability coefficients g（n，i）for a star-4-out-of-10：F system

5　总　结

star-k-out-of-n∶F系统可靠性系数计算公式的给出，有利于我们评价分析系统的可靠性和并据此进一步进行最优设计.

本文仅基于独立star-k-out-of-n∶F系统得到了可靠性系数.后续可研究非独立或元件失效概率不同情形下系统的可靠性系数；研究其他复杂系统的可靠性系数也是进一步的研究方向.

［1］PETAKOS K，TSAPELAS T.Reliability analysis for systems in a random enviroment［J］.Journal of Applied Probability，1997，34：1021-1031.

［2］LI Z H，ZHAO P.Reliability analysis on the δ-shock model of complex systems［J］.IEEE Transactions On Reliability，2007，56（2）：340-348.

［3］CHANG G J，CUI L R，HWANG F K.Reliabilities of Consecutive-k-out-of-n Systems［M］.Dordrecht，Netherlands：Kluwer Academic Publishers，2000.

［4］CHENG K，ZHANG Y L.Analysis for a consecutive-k-out-of-n：F repairable system with priorityin repair［J］. International Journal of Systems Science，2001，32（5）：591-598.

［5］CUI L R.The IFR property for consecutive-k-out-of-n：F systems［J］.Statist Probab Letters，2002，59（4）：405-414.

［6］CUI L R，HAWKES A G.A note on the proof for the optimal consecutive-k-out-of-n：G line for n≤2k［J］. Statis Plann Inference，2008，138（5）：1516-1520.

［7］GERA A E.A consecutive-k-out-of-n：G system with dependence elements-a matrix formulation and solution［J］.Reliab Eng Syst Saf，2000，68（1）：61-67.

［8］GUAN J C，WU Y Q.Repairable consecutive-k-out-of-n：F systems with fuzzy state［J］.Fuzzy Sets and Systems，2006，157（1）：121-142.

［9］JALALI A，HAWKES A G，CUI L R，et al.The optimal consecutive-k-out-of-n：G line for n≤2k［J］.Statist Plann Inference，2005，128：281-287.

［10］LAM Y，ZHANG Y L.Repairable consecutive-k-out-of-n：G systems［J］.Chinese J Trans，2000，4（3）：19-32.

［11］LIANG X L，LI Z H.Reliability analysis for consecutive-k-out-of-n：G repairable system［C］//Proceedings of the 4th International Conference on Quality and Reliability（ICQR）.2005：855-869.

［12］康庆德.组合学笔记［M］.北京：科学出版社，2009.

（责任编辑：李艺）

Reliability coefficient of star complex system

ZHANG Qi-bin1，SHA Xiao-cong2，WANG Na1，XU Hui-ping1，MA Ji1
（1.Gansu Computing Center，Lanzhou730030，China；2.Department of Computer Science and Technology，Lanzhou University，Lanzhou730030，China）

The reliability coefficients play an important role in the reduction of complex systems to a linear combination of parallel subsystems.This paper defines a new complex system，namely，star-k-out-of-n：F system，and calculates the reliability coefficients of this system.

reliability coefficient；complex system；star-k-out-of-n：F system

O213.5

A

10.3969/j.issn.1000-5641.2016.02.006

1000-5641（2016）02-0045-06

2015-02

张其斌，男，副研究员，研究方向为数学计算机.E-mail：qibin zhang@163.com.

沙孝聪，男，硕士研究生，研究方向为计算机应用.E-mail：475143533@qq.com.