A note on the commutativity of C∗-algebras
2016-11-11JIANGRunliang
JIANG Run-liang
(Department of Mathematics,Shanghai Normal University,Shanghai200234,China)
A note on the commutativity of C∗-algebras
JIANG Run-liang
(Department of Mathematics,Shanghai Normal University,Shanghai200234,China)
There are many characterizations for commutative C∗-algebras.In this note,we prove that a C∗-algebra A is not commutative if and only if there is a C∗-subalgebra B in A′′(the enveloping Von Neumann algebra of A)such that B is∗-isomorphic to M2(C). In terms of this result,we can recover some characterizations for the commutativity of C∗-algebras appeared before.
commutative C∗-algebras;enveloping Von Neumann algebra
Article ID:1000-5641(2016)02-0030-05
0 Introduction
There are many characterizations for commutative C∗-algebras.For examples,Kaplansky showed that a C∗-algebra A is commutative if and only if the only nilpotent element in A is 0(cf.[1,2.12.21]);Nakamoto in[2]gave a spectral characterization for the commutativity of a C∗-algebra;Ogasawara,Sherman,Wu,Ji and Tomiyama gave different characterizations of commutative C∗-algebras by means of the order structure,see[3-6]for details.In[7],Jeang and Ko proved that for non-constant continuous functions f and g defined on a closed interval I1and I2respectively,if f(x)g(y)=g(y)f(x)for all self-adjoint elements x and y in A with σ(x)⊆I1and σ(y)⊆I2,then A is commutative.
In this note,we give the following lemma that a C∗-algebra A is not commutative if and only if there is a C∗-subalgebra B in A′′(the enveloping Von Neumann algebra of A)such thatB is∗-isomorphic to M2(C).In terms of this result,we can recover some characterizations for the commutativity of C∗-algebras appeared in[3-7].
1 Basic Theories
Throughout the paper,C and R are the complex number field,the real number field respectively and A is always a C∗-algebra.If A has a unit e,we set σ(a)to be the spectrum of an element a∶σ(a)={λ∈C|λe-a is not invertible in A}.If A is non-unital,then we set σ(a)={λ∈C|λe-a is not invertible in},whereis the unitization of A.We put Asa={a∈A|a∗=a}.An element a of Asais positive if σ(a)⊆R+.We write a≥0 to mean a is positive,and denoted by A+the set of all positive elements of A.For a,b∈Asa,we write a≥b to mean a-b∈A+.Please see[8]for more details.
For convenience,we assume that A is a C∗-subalgebra of B(H)for certain complex Hilbert space H such that{a(ξ)|a∈A,ξ∈H}is dense in H,where B(H)is the C∗-algebra consisting of all bounded linear operators from H to H(cf.[8 Theorem 3.4.1]).Then A is strongly dense in A′′(cf.[8,Theorem 4.1.4]).For T∈B(H),let Ran(T)(resp.Ker T)denote the range(resp.null space)of T.
Recall that a continuous function f∶R→ C is called to be strongly continuous if for every Hilbert space K and each net{Tλ}λ∈Λ⊆B(K)saconverging strongly to an operator T∈B(K)sa,we have{f(Tλ)}λ∈Λconverges strongly to f(T).
The following lemma comes from[8,Theorem 4.3.2].
Lemma 1If f∶R→C is a continuous bounded function,then f is strongly continuous.
Recall from[5,Definition 1]that a continuous real-valued function f defined on a subset S of R is called to be operator monotonic increasing(resp.decreasing)on A associated with S if f(x)≤f(y)(resp.f(x)≥f(y))inwhenever x,y∈Asawith x≤y and σ(x)∪σ(y)⊆S.
Proposition 2Let f be a continuous real-valued function defined on R(or R+).If f is operator monotonic on A associated with R(or R+),then f becomes operator monotonic on A′′associated with R(or R+).
ProofWe just suppose that f is monotonic increasing on A associated with R.The proof of the remains is similar.
Let a,b∈(A′′)sawith a≤b.Set c=b-a≥0.By Kaplansky's density theorem(cf.[8,Theorem 4.3.3]),there are a net{aλ}λ∈Λ⊆Asaand a net{cλ}λ∈Λ⊆A+with‖aλ‖≤‖a‖and‖cλ‖≤‖c‖,∀λ∈Λ,such that aλconverges strongly to a and cλconverges strongly to c.Set bλ=aλ+cλ,∀λ∈Λ.Then‖bλ‖≤‖a‖+‖c‖,aλ≤bλ,∀λ∈Λ,and bλconverges strongly to b.
Put k=‖a‖+‖c‖and define a continuous real-valued function f0on R by
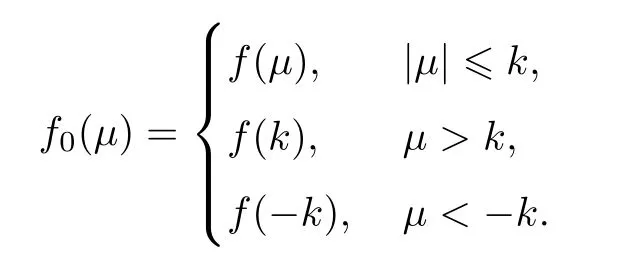
Since σ(a),σ(b),σ(aλ),σ(bλ)⊆[-k,k],∀λ∈Λ,we have

Noting that f0is continuous bounded function defined on R,by Lemma 1,f0(aλ)converges strongly to f0(a)and f0(bλ)converges strongly to f0(b),hence f(aλ)converges strongly to f(a)and f(bλ)converges strongly to f(b).Since f is operator monotonic increasing on A and aλ≤bλ,we have f(aλ)≤f(bλ),∀λ∈Λ,and consequently,f(a)≤f(b).
The next result is easy but useful.
Lemma 3Let A be a C∗-algebra.Then the following statements are equivalent∶
1.A is not commutative;
2.A′′is not commutative;
3.There exists a C∗-subalgebra B in A′′such that B is∗-isomorphic to M2(C).
ProofThe implications(1)⇔(2)and(3)⇒(2)are obvious.We now prove(2)⇒(3).
Since A′′is not commutative,it follows from[1,2.12.21]that A′′contains a non-zero nilpotent element a(i.e.,a2=0 and a≠0).Thus,Ran(a)⊆Kera.
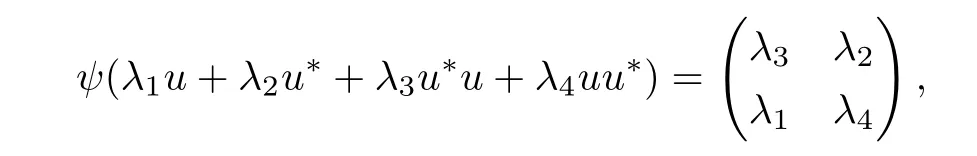
where λi∈C,i=1,2,3,4.It is easy to check that ψ is a∗-isomorphism.
2 Main Results
In this section,we will recover some characterizations for the commutativity of C∗-algebras appeared in[3-7]by using Lemma 3.
Definition 4We call a continuous monotone function f is matrix monotone of order n if f induces a monotone function on the matrix algebra Mn(C).
Combining Lemma 3 with Proposition 2,we have the following corollary proved in[6].
Corollary 5Let A be a C∗-algebra.If there exists a continuous monotone function f on R+(or R)which is not matrix monotone of order 2 but operator monotonic on A,then A must be commutative.
ProofIf A is not commutative,then A′′is not commutative either.Thus A′′has a C∗-subalgebra B which is*-isomorphic to M2(C).f is operator monotonic on A,so f must be operator monotonic on A′′,and f is also operator monotonic on B.Hence,f becomes a monotone function on M2(C),a contradiction.So A must be commutative.
Corollary 6Let A be a C∗-algebra.If A satisfies one of the following conditions,then A is commutative.
1.exp(x)≤exp(y)for all x,y∈A+with x≤y(cf.[5]);
2.x2≤y2for all x,y∈A+with x≤y(cf.[3]);
3.Let f+(t)=max{t,0}and f-(t)=-min{t,0},∀t∈R.For a∈Asa,put a+=f+(a)and a-=f-(a).If a≤b for a,b∈Asa,then a+≤b+(resp.b-≤a-)(cf.[4]).
Proof(1)Since exp(t)is not matrix monotone of order 2 by[6,Proposition 1],we obtain that A is commutative by Corollary 5.
For a,b∈Asawith a≤b,we have-b≤-a and hence(-a)-≤(-b)-by the assumption. Noting that(-a)-=a+and(-b)-=b+,we get the assertion by above argument.
Corollary 7Let f and g be non-constant continuous functions defined on closed intervals I1and I2respectively.Suppose that there exist non-zero elements xi∈Asawith σ(xi)⊆Ii,i=1,2.If f(x)g(y)=g(y)f(x)for all x,y∈Asawith σ(x)⊆I1and σ(y)⊆I2,then A is commutative.
ProofAssume that I1=[µ1,µ2]and I2=[µ3,µ4].We first show that for x,y∈(A′′)sa. with σ(x)⊆I1and σ(y)⊆I2,f(x)g(y)=g(y)f(x).
If A is unital,by Kaplansky's density theorem,there exist two nets{xλ}λ∈Λand{yλ}λ∈Λin A+such that‖xλ‖≤‖x-µ1‖,‖yλ‖≤‖y-µ3‖,∀λ∈Λ,and xλ(resp.yλ)converges strongly to x-µ1(resp.y-µ3).Thus,σ(xλ+µ1)⊆I1,σ(yλ+µ3)⊆I2,∀λ∈Λ,and xλ+µ1(resp.yλ+µ3)converges strongly to x(resp.y).Extend f and g to the continuous bounded functions on R by

by the hypothesis,we get that f(x)g(y)=g(y)f(x)by Lemma 1.
If A is non-unital,then I1and I2contain 0.Setwhenµ1=0 orµ2=0 and=[-s,s]when s=min{-µ1,µ2}>0.Then⊆I1and for each x∈(A′′)sawith σ(x)⊆there is a net{xλ}λ∈Λ⊆Asawith σ(xλ)⊆∀λ∈Λ,such that xλconverges strongly to x by Kaplansky's density theorem.Similarly,there exists a closed intervalin I2such that for each y∈(A′′)sawith σ(y)⊆we can find a net{yλ}λ∈Λin(A′′)sawith σ(yλ)⊆,∀λ∈Λ, such that yλconverges strongly to y.Therefore,f(x)g(y)=g(y)f(x)for any x,y∈(A′′)sawith σ(x)⊆and σ(y)⊆by Lemma 1.
Now suppose that A is not commutative.Then there is a C∗-subalgebra B in A′′such that B is∗-isomorphic to M2(C).Thus,we have f(x)g(y)=g(y)f(x)for any x,y∈M2(C)sawith σ(x)⊆and σ(y)⊆LetandSet
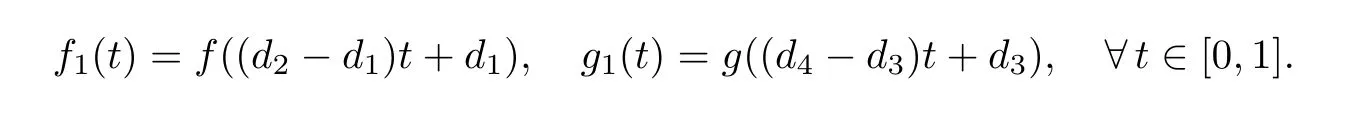

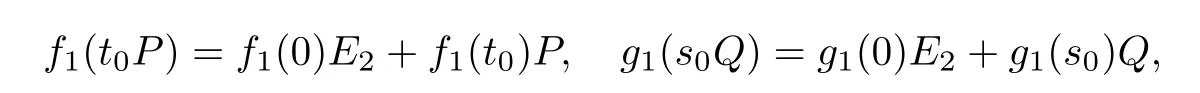
[References]
[1]DIXMIER J.C*-Algebras[M].New York:North-Holland,1977.
[2]NAKANOTO R.A spectral characterization of commutative C*-algebras[J].Mathematica Japonica,1979,24:399-400.
[3]OGASAWARA T.A theorem on operator algebras[J].Journal of Science of the Hiroshima University,1955,18:307-309.
[4]SHERMAN S.Order in operator algebras[J].American Journal of Mathematics,1951,73(1):227-232.
[5]WU W.An order characterization of commutativity for C*-algebras[J].Proceedings of the American Mathematical Society,2000,129:983-987.
[6]JI G X,TOMIYAMA J.On characterizations of commutativity of C*-algebras[J].Proceedings of the American Mathematical Society,2003,131:3845-3849.
[7]JEANG J,KO C.On the commutativity of C*-algebras[J].Manuscripta Mathematica,2004,115:195-198.
[8]MURPHY J G.C*-Algebras and Operator Theory[M].San Diego:Academic Press,1990.
(责任编辑:林磊)
10.3969/j.issn.1000-5641.2016.02.004
C∗-代数交换性简谈
蒋闰良
(上海师范大学 数学系,上海200234)
交换C∗-代数有许多特征.在本文中,证明了C∗-代数A是非交换的当且仅当其包络冯诺依曼代数A′′中有一个C∗-子代数B,B∗-同构于2阶矩阵代数M2(C).基于这个性质,又可以得到一些旧命题的新证明方法.
交换C∗-代数;包络冯诺依曼代数
2015-03
蒋闰良,男,博士后,研究方向为算子代数.E-mail:Eugene-Jiang@126.com.
O212.4Document code:A
