基于ramp损失函数的原空间支持向量机

袁玉萍，安增龙

（1.黑龙江八一农垦大学 信息与计算科学系，黑龙江 大庆163319；2.黑龙江八一农垦大学 经济管理系，黑龙江 大庆163319）

基于ramp损失函数的原空间支持向量机

袁玉萍1，安增龙2

（1.黑龙江八一农垦大学 信息与计算科学系，黑龙江 大庆163319；2.黑龙江八一农垦大学 经济管理系，黑龙江 大庆163319）

针对传统支持向量机对噪声敏感的问题，给出一种基于不对称形式的二次不敏感控制型ramp损失函数的支持向量回归机，采用凹凸过程优化和光滑技术算法，将非凸优化问题转化为连续且二次可微的凸优化问题，利用有限步终止的Amijo-Newton优化算法，求解所建立的优化模型，并分析了算法的收敛性.该算法不仅可以保持支持向量的稀疏性，而且还可以控制训练样本中的异常值.实验结果表明，该模型保持了很好的泛化能力，无论对模拟数据还是标准数据都具有一定的拟合精度，与标准支持向量机模型相比，不仅能够降低噪声和孤立点的影响，而且也具有较强的鲁棒性.

支持向量回归机；异常值；损失函数；凹凸过程

0　引言

由于标准支持向量机对所有输入样本同等对待，在训练时从中选取部分样本，利用支持向量机来构造最终的决策函数，同时标准支持向量机对异常值也非常敏感，在确定决策超平面时所起到的作用非常大，降低了支持向量机的泛化能力和推广能力.因此当样本中含有噪声时，建立支持向量机的鲁棒性模型是非常重要的.

为了抑制支持向量机对噪声或野点的影响，提高模型的泛化能力，很多学者在此方面做了大量工作［1-4］.减少或限制噪声样本损失的方法基本分为两类.一类是将模糊技术应用到支持向量机中.台湾学者Lin等在2002年提出了模糊支持向量机方法（Fuzzy Support Vector Machine，FSVM）［5-6］，将模糊技术应用于支持向量机中，根据不同输入样本对训练的贡献不同赋以不同的隶属度，对噪声或野点赋以较小的隶属度以减小它们对模型的影响，对噪声样本乘以较小的模糊因子，使得在构造目标函数时，不同的样本有不同的贡献，从而达到降低或者消除噪声样本的目的.文献［7］通过估计训练样本为噪声点的可能性大小来调节隶属度，如果一个训练样本点更接近不属于自己的另一类，则将该点以较高的概率被看做噪声；另一类是通过构造新的损失函数以减少或者限制噪声样本的损失［8-9］.2006年Xu和Crammer等人建立了基于截断的Hinge损失的鲁棒支持向量机模型［10］，是对Hinge损失函数的一个很好的替代，该模型是一个非凸非光滑的优化问题，利用光滑ramp损失函数和凹凸过程优化算法进行求解.2008年Wang等人提出两分类问题的鲁棒支持向量机，利用非凸的不可微的ramp损失函数构造优化模型，采取concave-convex procedure（CCCP）凹凸过程将非凸优化问题转化为凸优化问题，再利用经典的牛顿算法求解［11］.在同一年，Zhao等人在上述方法的基础上，提出了基于不敏感损失函数的控制型损失函数，将基于控制型损失函数应用到鲁棒支持向量回归机问题［12］.Xu等人针对hinge控制型损失函数提出了针对异常值剔除的鲁棒支持向量机，并且将优化问题转化为一个半定规划问题［13］.

综合上述分析，文献［12］是针对两分类问题提出的ramp损失函数，文献［13］提出了基于不敏感的控制型一次损失函数.由于二次不敏感损失函数在一定范围内函数变化较快，在二次方区域内对符合高斯分布的噪声具有较强的抑制作用，并且具有稀疏性，在底部的光滑性比一次不敏感损失函数好等优点，因此，本文提出基于二次不敏感控制型ramp损失函数的不对称形式鲁棒支持向量回归机，弱化异常值的干扰，其分段损失函数对落在不同区间的误差项采用不同的惩罚函数形式.

1　Ramp不对称形式鲁棒支持向量回归机

1.1原空间支持向量回归机

原空间鲁棒支持向量回归机模型∶对于随机产生的训练样本回归问题其中xi∈Rn是输入指标，yi是相对应的函数值.基于ε-不敏感损失函数支持向量机算法为∶

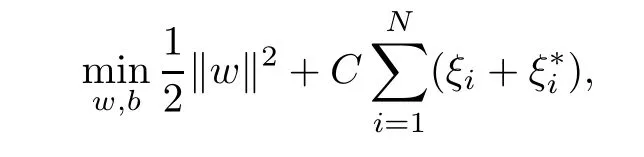
使得

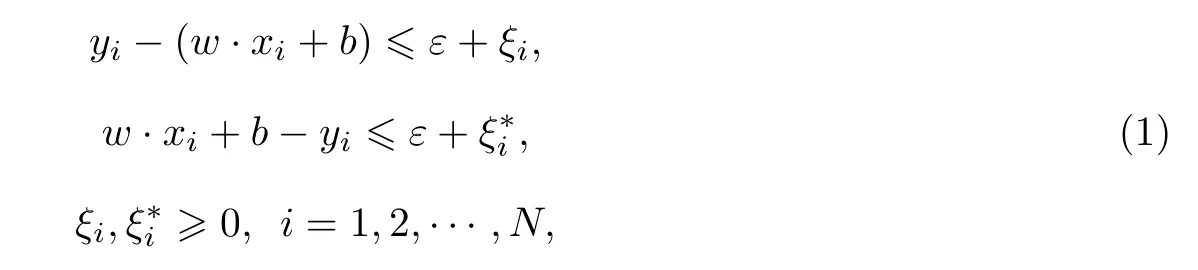
这里，C是调节模型的复杂性和训练的错误的一个折中，在（1）中消去松弛变量1,2,···,N,得到无约束优化问题∶

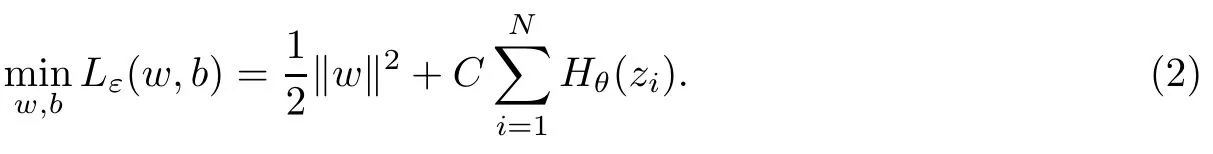
选取二次不敏感控制型ramp损失函数不对称形式Hθ（zi）=min（θ2,HA（zi））,其中，

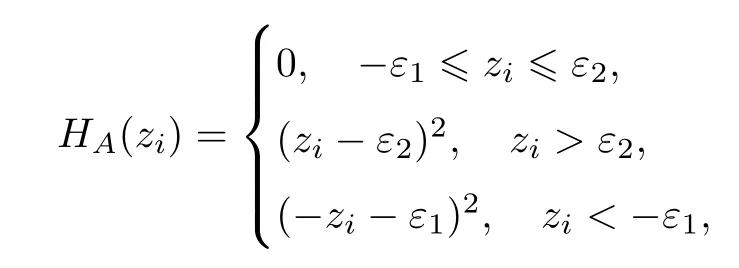
zi=w·xi+b-yi,ε1＜ε2.综合上式提出的ramp损失函数为∶

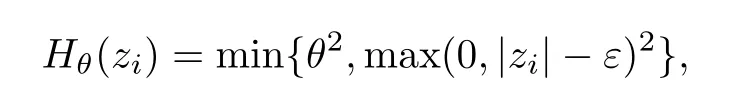
即损失函数的值在（0,θ2）这个区间内，θ为参数，显然限制了样本的损失.为了简单起见，在不影响模型的泛化性能情况下先不讨论偏执b项，同时引入核函数策略及转化到希尔伯特空间H，得到优化问题∶

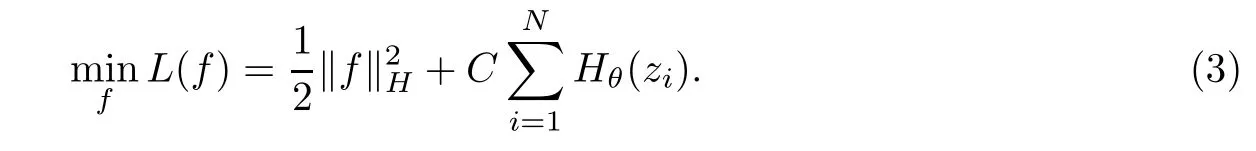
由表现定理［14］，（3）式的优化函数f可以表示为∶

将（4）式代入（3）式，得∶

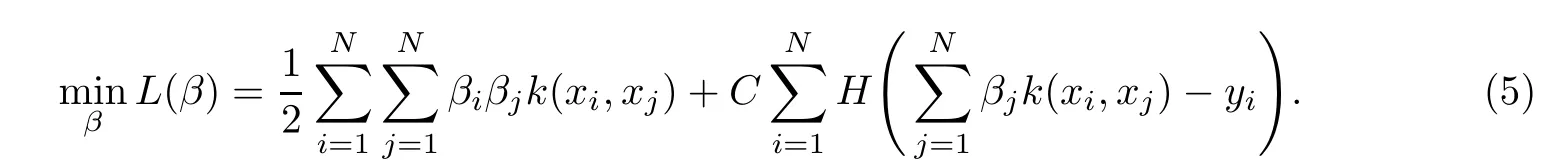
令β=［β1,β2,···,βN］T，K为核矩阵，其中Kij=k（xi,xj）,i,j=1,2,···,N，可将（5）式变形为∶

1.2光滑非凸损失函数的建立

由于Hθ（z）函数既不光滑也不是凸函数，难以应用凸优化方法对相应的支持向量回归机模型求解，因此，需要将其进一步转化为光滑且凸的损失函数，构造两个huber损失函数不对称形式∶

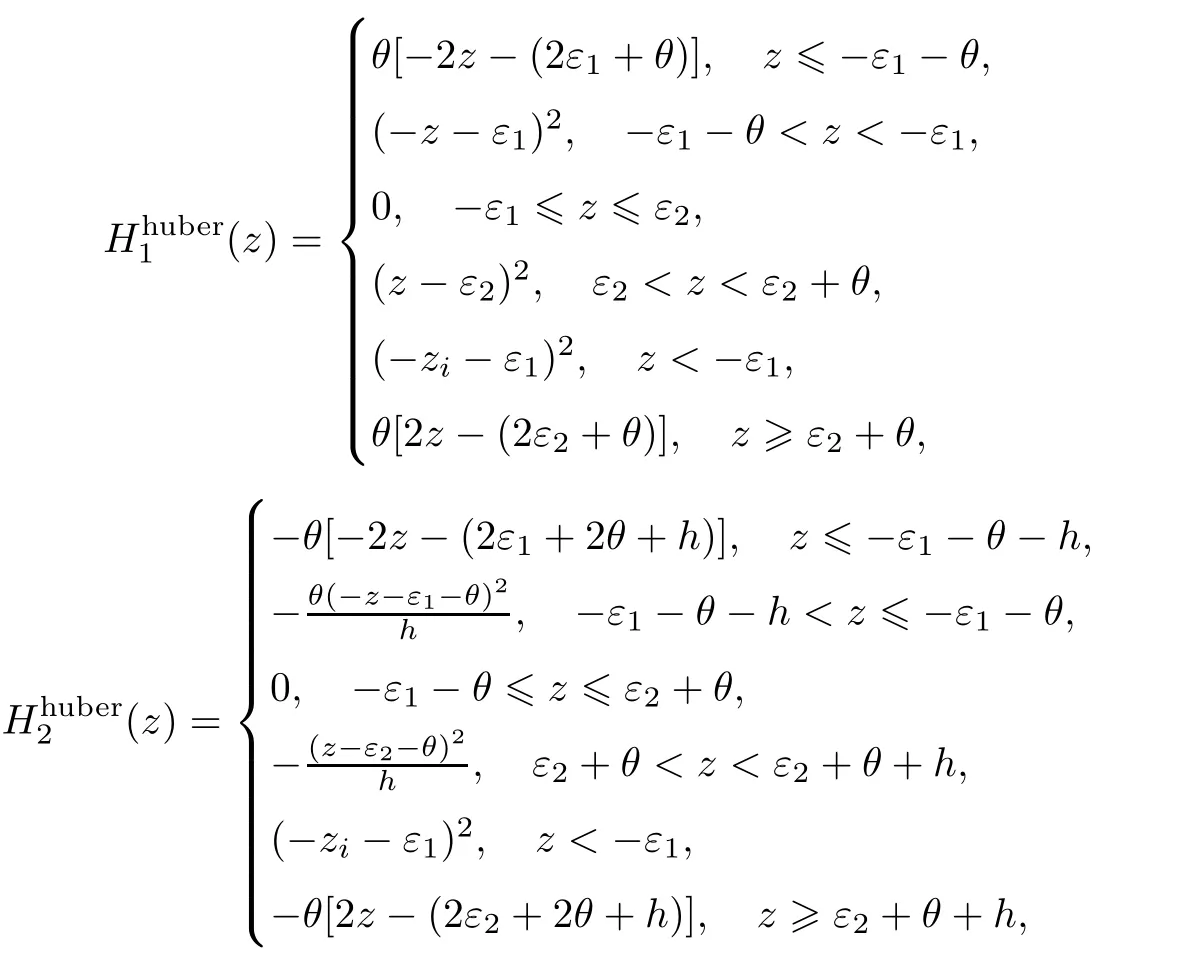
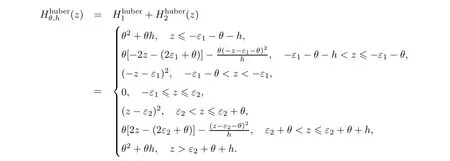
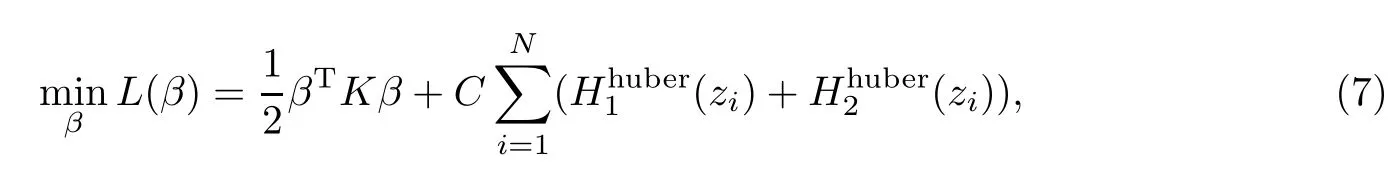
其中zi=-yi,i=1,2,···,N.对于（7）式，不能直接使用凸优化技术解决.所建立的光滑非凸的损失函数见图1.

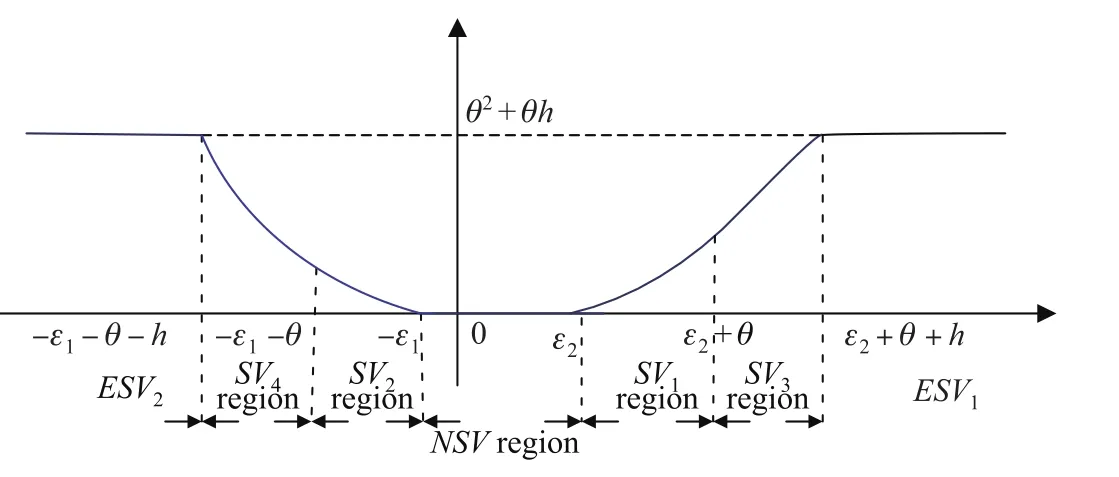
图1　光滑非凸的损失函数Fig.1　Smooth non-convex loss function

1.3利用凹凸过程将非凸函数转仁为凸函数

凹凸过程（Concave-Convex Procedure，CCCP）［15］是用于求解非凸形式的优化问题.假设目标函数E（θ）可以写成一个凹函数Ecav（θ）和一个凸函数Evex（θ）的和式，即E（θ）= Ecav（θ）+Evex（θ），求E（θ）的最小值.凹凸过程如下∶

（i）初始化变量θ；

（ii）计算θi+1=argminθ（Evex（θ）+（θi）·θ），直到θi收敛；

（iii）输出θ=θi.

为了利用CCCP过程，将式（7）分解为凸函数和凹函数两部分∶

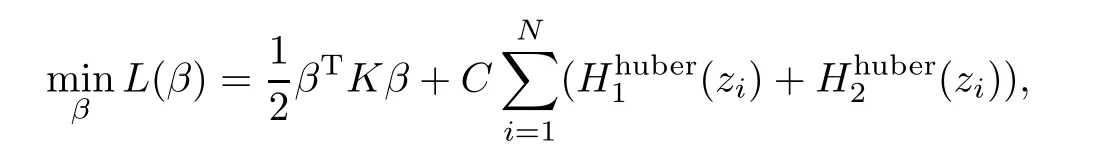
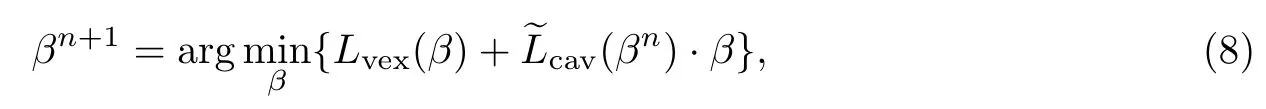
其中βn是前一次CCCP迭代中获得的解，而是Lcav（β）对变量β的一阶导数在βn点的值.

利用CCCP算法，将（7）式转化为在原空间一个凸的、光滑的优化问题（10）式，这样对于（10）式就可以利用比较成熟的凸优化方法来解决.

2　Amijo-Newton算法实现及收敛性分析

2.1有限步终止的Amijo-Newton算法［16］

（1）样本点位于-ε1＜zi＜ε2区域的训练样本称为非支持向量，样本集合为NSV区域，样本数记为|NSV|；

（2）样本点位于ε2＜zi＜ε2+θ+h或-ε1-θ-h＜zi＜-ε1的训练样本称为支持向量.具体地，可将上述集合分为4个子集合∶样本点位于ε2＜zi＜ε2+θ，或-ε1-θ＜zi＜-ε1，区域的训练样本分别称为支持向量SV1、SV2，样本数记为|SV1|、|SV2|；

样本点位于ε2+θ＜zi＜ε2+θ+h，或-ε1-θ-h＜zi＜-ε1-θ，区域的训练样本分别称为支持向量SV3、SV4，样本数记为|SV3|、|SV4|；

（3）样本点位于zi＞ε2+θ+h或zi＜-ε1-θ-h的训练样本分别称为错误支持向量ESV1、ESV2，样本数为|ESV1|、|ESV2|.

为了方便，根据上述的七个区域将训练样本按照SV1,SV2,SV3,SV4,ESV1,ESV2,NSV的顺序排列，定义均为N×N的对角矩阵，表示阶的单位矩阵，表示|SV2|阶 0矩阵.同理，定义

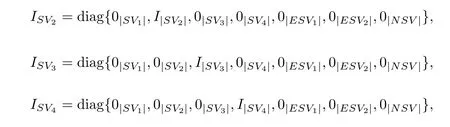
对目标函数（10）式求关于β的梯度表达式∇L（β）及Hesse矩阵H∶

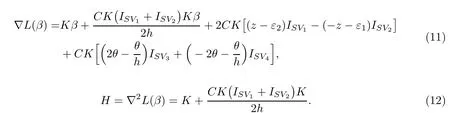
搜索方向为∶

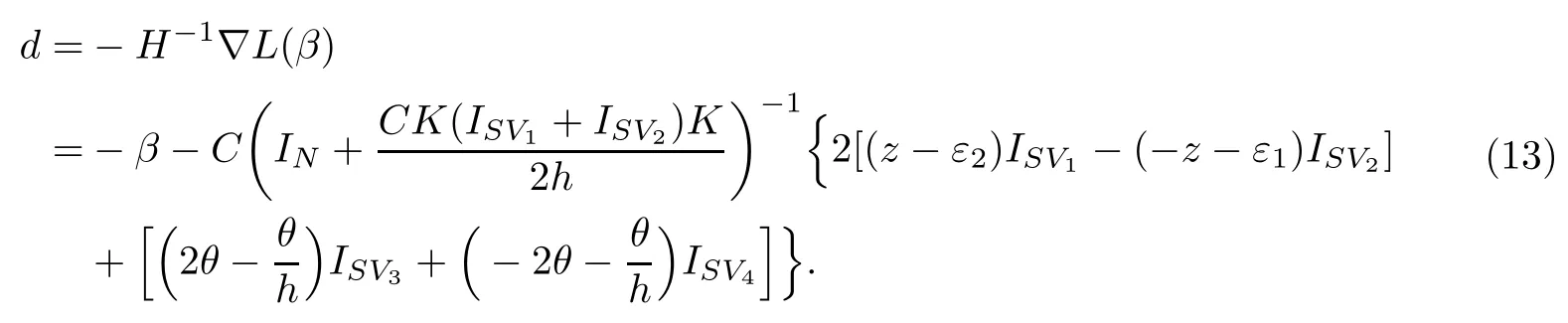
迭代公式为∶

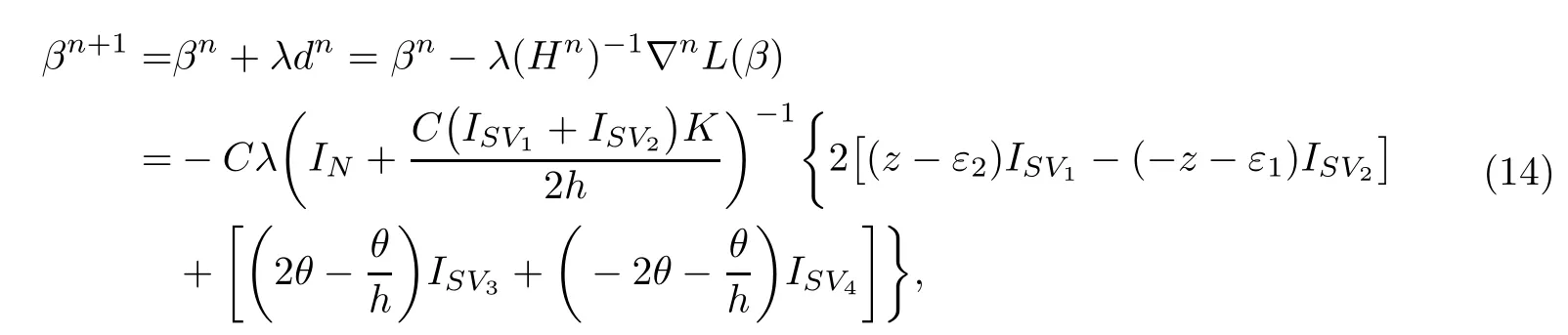
λ为搜索步长，即可得到（10）式的最优解.但是，如果当样本点的个数N比较大时，每步都直接计算的逆矩阵，要占计算机很大的空间，大大影响运算效率，因此，重新改写它的形式为∶

该矩阵的逆矩阵是个稀疏矩阵.

由（14）式得到最优解βn+1，其分量的最优解即位于这两个区域的异常值和非支持向量对决策函数没有任何影响，得到决策函数∶

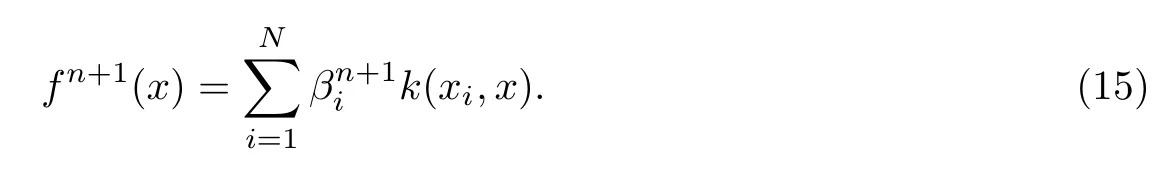
因此，原空间的鲁棒支持向量回归机在求解过程中，保持对异常值的不敏感性，从而具有更优的泛化能力.采取有限步终止的Amijo-Newton算法求解（10）式，具体算法如下∶

Step 2.根据|z0|=|f0（x）-y|区域的大小将训练样本分成七类∶SV1,SV2,SV3,SV4, ESV1,ESV2,NSV；

Step 3.计算梯度∇nL（β），若‖∇nL（β）‖≤ρ，则停止计算，否则转下一步；

Step 4.令λk=max｛1,1/2,1/4,···｝为Amijo步长，且使得不等式L（βk）-L（βk+成立；

Step 5.根据（14）式计算βn+1，由（15）式得到函数fn+1（x），转step 2.

2.2算法收敛性

命题1由有限步终止的Amijo-Newton算法对目标函数（10）式求解，所得到的序列βn是单调递减的.

证明由（7）式，minβ其中是凸部分，是凹部分.若βn+1是该算法对目标函数（10）式的第n次迭代时得到的最优解，则有∶

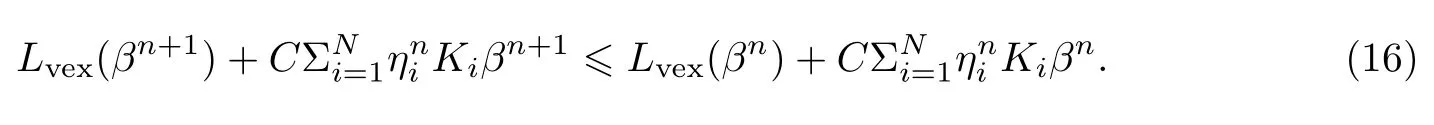
又根据凹函数的性质，有

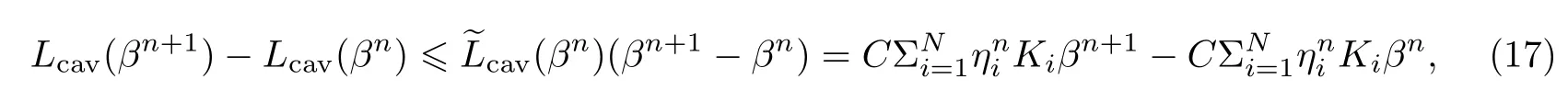
说明该算法是单调下降的.又由于目标函数L（β）≥0，即有下界，故该算法收敛.

3　数据试验

为了验证提出的鲁棒支持向量回归机的有效性，分别对模拟数据和标准的UCI数据集进行数值试验.将本文算法与标准支持向量回归机进行比较，通过试验可以看出本文算法能够有效地抑制异常值对决策超平面的影响.对于非线性回归问题文中采用高斯核函数（RBF）∶

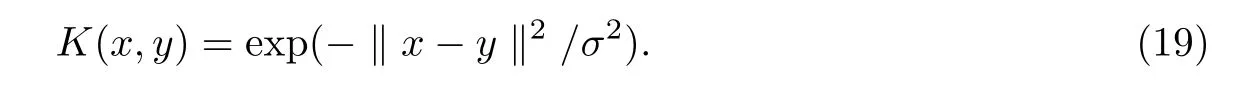
在试验中有6个参数ε1,ε2,θ,C,σ,h，最优参数（C,σ）采取网格搜索获得，搜索区间为｛2-5,2-4,···,24,25｝×｛2-5,2-4,···,24,25｝.参数h表示光滑ramp损失函数因子，取值较小；θ是惩罚函数的上界，一般数值设置在0.1∽10之间.如果θ值取得较大，容易将异常值视为支持向量，增加支持向量的个数，导致运行速度减慢.如果θ值取得较小，容易将正常值视为异常值，使一些正常值不能参与训练，导致算法降低泛化能力.

采用均方根误差（RMSE）衡量回归算法性能的评价指标.实验环境为Matlab 7.0，Windows XP，内存2 GB，主频2.99 GHz.

3.1人工数据集试验

设样本集T=｛（x1,y1）,（x2,y2）,···,（x300,y300）｝，其中，xi,i=1,2,···,300，均匀分布在区间［-4,4］，yi=sin（3xi）/（3xi）+γi,i=1,2,···,300,γi∽N（0,0.12），任意选取200个样本点为训练点，其余的为测试点.将上述数集进行两次测试，分别利用最小二乘支持向量机（LS-SVR）和本文算法进行训练和预测，预测结果如图2、图3.

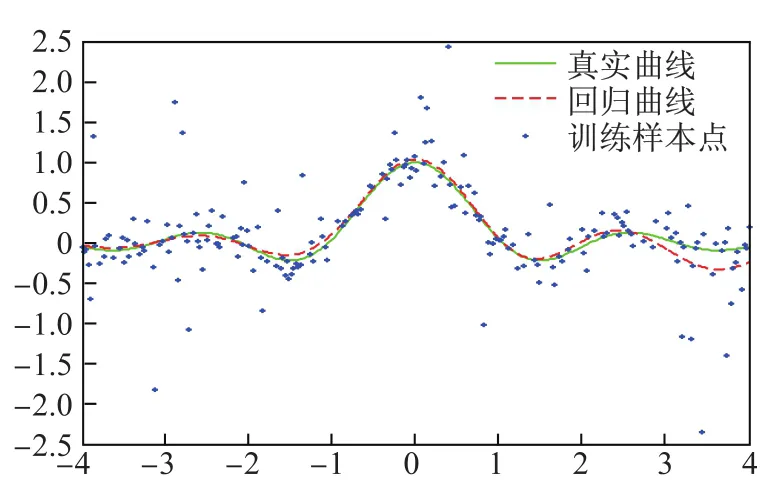
图2　最小二乘（LS-SVR）算法Fig.2　The algorithm of least square support vector regression（LS-SVR）

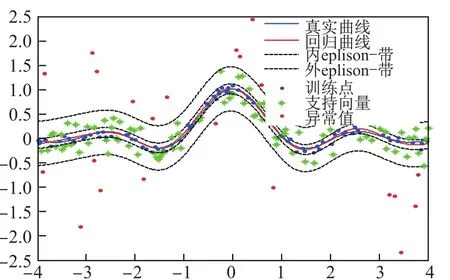
图3　本文算法Fig.3　Algorithm in this paper

由图中可以看出，这两种支持向量机算法都可以较准确地反映函数yi=sin（3xi）/（3xi）的整体趋势.由于本文提出的算法对异常值所造成的损失设置了惩罚上界，抑制异常值对模型的影响，因此在预测过程中表现出比最小二乘法具有更高的预测精度.两种算法的实验结果如表1.另外，最小二乘支持向量机所有的样本均为支持向量，而本文提出算法异常值被区分开，不参与最终决策函数的构成，因此在运行时间上也提高了运算效率.

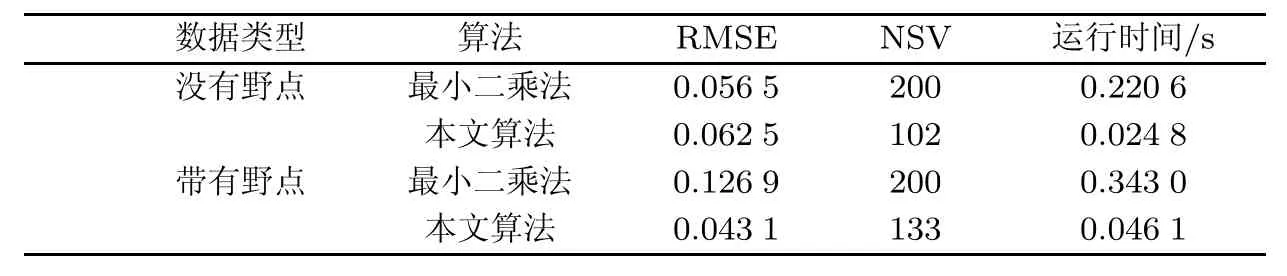
表1　人工数据集高斯噪声的试验结果Tab.1　The experimental results on artificial data sets

3.2标准的UCI数据集的试验

为了进一步检验本节提出的算法性能，选取标准数据库中的数据集作为试验数据集，实验数据来源于UCI数据库（http∶//archive.ics.uci.edu/ml/）、StatLib数据库（http∶//lib.stat.cmu. edu/datasets/）.数据集的统计信息见表2.

表2　数据集的统计信息Tab.2　Statistical information on data set

为了比较算法的性能，将本文算法、NP-RSVR-NCLF（N-R-N）算法［10］及LS-SVR算法的试验结果进行比较，比较结果见表3.

表3　NP-RSVR-NCLF算法、LS-SVR算法和本文算法的标准UCI数据集的试验结果对比Tab.3　Comparison of the experimental results of standard UCI data set with NP-RSVR-NCLF algorithm，LS-SVR algorithm and the algorithm in this paper

表3中数据结果是10次试验的平均值，由试验结果可以看到本文算法在各数据集上的误差率比LS-SVR算法小很多，与NP-RSVR-NCLF算法误差率相当.另外，一个算法的效率也是非常重要的，可以看出本文提出的算法所对应的衡量预测精度指标均小于LS-SVR，而且具有较好的稳定性，支持向量的个数比较少，提高了运行速度，运行的时间同时也明显减少.

4　结论

本文提出了原空间非凸不对称形式损失函数鲁棒支持向量机，利用CCCP过程将非凸优化问题转化为连续可微的凸优化问题，利用带步长的Armijo-Newton算法进行求解.该非凸损失函数不仅保持了支持向量回归机的稀疏性，而且在一定程度上控制了训练点中的异常值，从而可以增强泛化性能，在对性能影响很小的情况下，最大程度减少支持向量的冗余程度.通过模拟和真实的标准数据集上的实验，验证了本文所提出的算法的有效性.

［1］TSUJINISHI D，ABE S.Fuzzy least squares support vector machines for multiclass problems［J］.Neural Networks，2003，16（5/6）：785-792.

［2］XIU F J，ZHANG Y，JIAN C L.Fuzzy SVM with a new fuzzy membership function［J］.Neural Computing and Application，2006（15）：268-276.

［3］LIU Y H，CHEN Y T.Face recongnition using total margin-based adaptive fuzzy support vector machines［J］. IEEE Trans on Neural Networks，2007，18（1）：178-192.

［4］YU S，YANG X W，HAO Z F，et al.An adaptive support vector machine learning algorithm for large classification problem［J］.Lecture Notes in Computer Science，2006，3971：981-990.

［5］LIN C F，WANG S D.Fuzzy support vector machines［J］.IEEE Transactions on Neural Networks，2002，3（2）：464-471.

［6］JIN B，ZHANG Y Q.Classifying very large data sets with minimum enclosing ban based support vector machine［C］//Proceedings of the 2006 IEEE International Conference on Fuzzy Systems.Vancouver BC，2006：364-368.

［7］BO L，WANG L，JIAO L.Recursive finite Newton algorithm for support vector regression in the primal［J］. Neural Computation，2007，19（4）：1082-1096.

［8］CHEN X B，YANG J，LIANG J，et al.Recursive robust least squares support vector regression based on maximum correntropy criterion［J］.Neurocomputing，2012，97：63-73.

［9］杨俊燕，张优云，朱永生.不敏感损失函数支持向量机分类性能研究［J］.西安交通大学学报，2007，4l（11）：1315-1320.

［10］HUANG H，LIU Y.Fuzzy support vector machines for pattern recognition and data mining［J］.International Journal of Fuzzy Systems，2002，4（3）：3-12.

［11］WANG L，JIA H，LI J.Training robust support vector machine with smooth ramp loss in the primal space［J］Neurocomputing，2008，71（13/14/15）：3020-3025.

［12］ZHAO Y，SUN J.Robust support vector regression in the primal［J］.Neural Networks，2008，21（10）：1548-1555.

［13］YANG S H，HU B G.A stagewise least square loss function for classfication［C］//Proceedings of the SIAM International Conference on Data Mining.2008，120-131.

［14］KIMELDORF G S，WAHBA G.A correspondence between Bayesian estimation on stochastic processes and smoothing by splines［J］.Annals of Mathematical Statistics，1970，41（2）：495-502.

［15］YUILLE A L，RANGARAJAN A.The concave-convex procedure（CCCP）［J］.Neural Computation，2003，15（4）：915-936.

［16］FUNG G，MANGASARIAN O L.Finite Newton method for Lagrangian support vector machine classification［J］.Neurocomputing，2003，55（1/2）：39-55.

（责任编辑：林磊）

Support vector machine in the primal space based on the ramp loss function

YUAN Yu-ping1，AN Zeng-long2
（1.College of Sciences，Heilongjiang Bayi Agricultural University，Daqing Heilongjiang 163319，China；2.College of Economics&Management，Heilongjiang Bayi Agricultural University，Daqing Heilongjiang163319，China）

Aiming at the problem of standard support vector machine being sensitive to the noise，a new method of support vector regression（SVR）machine based on dissymmetry quadratic and controlled-insensitive loss function is proposed.Using the concave and convex process optimization and the smooth technology algorithm，the problem of non-convex optimization is transformed into the problem of the continuous and twice diferentiable convex optimization.Using the Amijo-Newton optimized algorithm of finiteiteration termination，the established optimization model is solved，and the convergence of the algorithm is analyzed.The algorithm can not only keep the sparse nature of support vector，but also control the abnormal values of the training sample.The results of the experiment showed that the support vector regression machine model proposed kept good generalization ability，and the model could fit better both the simulated data and the standard data.Compared with the standard support vector machine（SVM）model，the proposed model not only can reduce the efects of noise and outliers，but also has stronger robustness.

support vector regression；outliers；loss function；concave-convex procedure

TP181；TP391

A

10.3969/j.issn.1000-5641.2016.02.003

1000-5641（2016）02-0020-10

2015-03

高等学校博士学科点专项科研基金（20112305110002）；黑龙江八一农垦大学博士科研启动基金（XDB2015-23）；黑龙江农垦总局科研资助项目（HNK11A-14-07）

袁玉萍，女，博士，研究方向为运筹学与优化.E-mail：byndyyps@sina.com.

安增龙，男，教授，研究方向为人力资源管理.E-mail：anzl@2001@163.com.