邂逅拐点设置障碍,让学生的思维多飞一会儿
2016-11-11江苏滨海县实验小学224500徐荣书
江苏滨海县实验小学(224500) 徐荣书
邂逅拐点设置障碍,让学生的思维多飞一会儿
江苏滨海县实验小学(224500)徐荣书
在小学数学教学中,当学生思维遇到拐点时,教师要做的就是提供空间和时间,搭建平台,让学生充分思考和自主探索,帮助学生形成反思、质疑等数学思维能力。
小学数学教学策略发展思维最近发展区
在小学数学教学中,当学生位于最近发展区,已有知识和新知之间进行迁移时,将会面临三个思维的拐点:概念易混点,思路盲动点,方法构建点。此时,教师要做的就是提供充足的空间和时间,在拐点处设置障碍,带领学生经历知识形成的过程,培养学生的思维能力。
一、在概念易混点设置障碍,让思维多飞一会儿
很多数学概念和定理法则是数学学习的基础,在进行这些基础建构的时候,如果有一点点错误,都容易为进一步学习带来阻碍。因此,教师可以围绕思维拐点设置一些障碍,引发学生自主思维,通过比较、辨析等多种活动,深化学生对数学概念、公理、法则等知识的建构。
比如,在教学三角形的分类时,为了让学生能够直观理解锐角三角形、钝角三角形和直角三角形,笔者用多媒体向学生呈现3个三角形当中的某一个角,让学生判断这3个三角形分别是什么三角形:
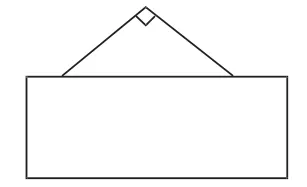
图1
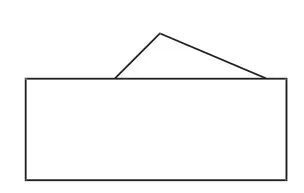
图2
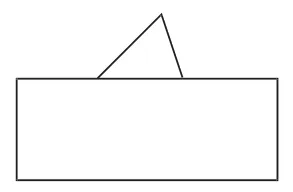
图3
对图1和图2,学生能够很快判断出三角形分别为直角三角形和钝角三角形,而在图3中,学生不假思索地判断三角形为锐角三角形。此时我故意设置障碍:“真的确认是锐角三角形吗?说出你的理由。”学生逐步认识到:判断一个三角形是否是锐角三角形,只根据露出的一个锐角是不能确定的,而是需要知道这3个角是否都是锐角。由此,学生对锐角三角形有了清晰的认识。在这个教学过程中,学生提出了新的问题:为什么有一个角是直角的三角形一定是直角三角形?有一个角是钝角的三角形一定是钝角三角形吗?根据学生的疑问,我继续引导:“每个三角形至少有两个锐角吗?可能与三角形的什么有关?”学生的思维被逐步打开,为进一步的学习奠定了基础。
以上环节,教师围绕学生的思维拐点,通过数学障碍的设置,帮助学生在尝试和比较中巩固了锐角三角形的特点,为学生后继学习建立起积极的心理状态。
二、在思路盲动点设置障碍,让思维多飞一会儿
由于年龄小,学生在解决问题时常常会陷入思维混沌的盲动状态。此时,教师要紧紧抓住思维的拐点,精心设置障碍,帮助学生消除盲动点。
比如,应用题:小丽将自己积攒的画片的一半还多6张送给了小冉,还剩下24张。请问小丽原来有多少张画片?学生列出算式:24÷2+6;24÷2-6;24×2-6,(24+6)÷2……从这些解答方式不难看出,由于受到定式思维的影响,学生看到题目中有“一半”这个词,就产生了要除以2的盲动思维;有的看到“还多”这个词,就产生了要用加法的盲动思维。由于没有设定的目标,数量关系不够清晰,因而给学生带来了很多困扰。基于此,我设置了如下障碍:小丽原有的画片比24张多还是少?为什么?如果小丽将自己画片的一半还多6张送给小冉,还剩下的比一半多还是比一半少?画片的一半正好是多少张?通过解决这些问题,学生学会运用倒推的方法进行分析,从而找到解决的办法。
教师在学生的思路盲动点处设置障碍,让学生的思维多飞一会儿,帮助学生克服了定式思维所造成的负迁移,大大提升了学生解决问题的能力。
三、在方法构建点设置障碍,让思维飞一会儿
在小学数学教学中,教师要引导学生构建问题解决的方法,这个构建点正是思维的拐点。此时,教师要紧扣这个方法点设置障碍,带领学生进行比较和深入探究。
比如,习题:要将一张长48厘米、宽32厘米的长方形纸裁成长为6厘米、宽为4厘米的小长方形纸片,最多能裁多少个?不少学生用“总面积÷每个小长方形的面积”,列出算式“48×32÷(6×4)=64(张)”。此时我设置了障碍:将宽为32厘米改为29厘米。学生还按照之前的办法列式“48×29÷(6×4)=58(张)”。我画出图4,并追问:“这样能正好裁完而没有剩余吗?对比两道题,看看如何解决?”学生发现,原有方法并不能对所有条件都适合,需要考虑余下的能不能继续裁,由此列出算式“29÷4=7(个)……1(厘米),48÷6×7=56(张)”。
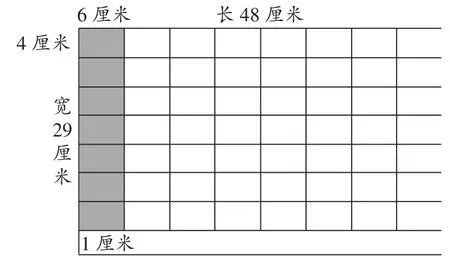
图4
教师在方法构建点设置障碍,带领学生在冲突中生成新的解决方法,发展了学生的数学能力。
总之,在小学数学教学中,教师要抓住有利时机设置障碍,让学生的思维多飞一会儿。
(责编童夏)
G623.5
A
1007-9068(2016)29-090
